1.1.2 等边三角形的性质同步练习(含解析)-北师大版数学八年级下册
文档属性
| 名称 | 1.1.2 等边三角形的性质同步练习(含解析)-北师大版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 90.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 20:35:05 | ||
图片预览

文档简介
1.1.2 等边三角形的性质
刷基础
知识点1 等腰三角形中的相等线段
1[2023山西晋中调研]如图,在△ABC中,AB=AC,给出的下列条件中,不能使BD=CE的是( )
A. BD,CE 分别为AC,AB 边上的高
B. BD,CE 分别为AC,AB 边上的中线
D.∠ABD=∠BCE
2[2024上海宝山区期末]已知:如图,△ABC 是等腰三角形,AD 是底边上的中线,DE 和 DF分别垂直于 AB,AC,垂足分别为点 E,F.求证:AE=AF.
知识点2 等边三角形的性质
3如图,以O为圆心,任意长为半径画弧,与射线OA交于点 B,再以 B为圆心,BO 长为半径画弧,两弧交于点 C,画射线OC,则∠O 的度数为( )
A.30° B.45° C.60° D.75°
4[2024四川成都二模]如图,直线m∥n,△ABC是等边三角形,顶点 B 在直线n上,直线m交AB于点E,交AC于点 F,若∠1=140°,则∠2的度数是 ( )
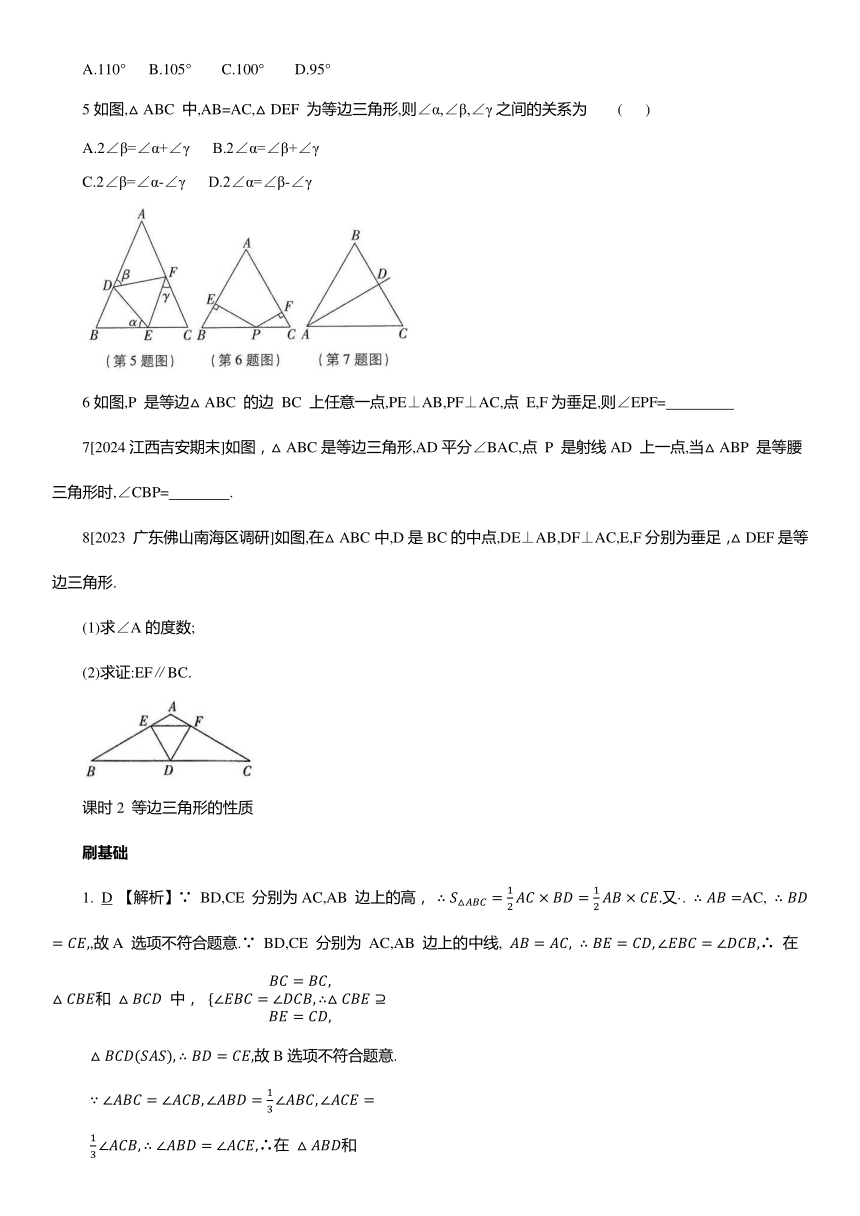
A.110° B.105° C.100° D.95°
5如图,△ABC 中,AB=AC,△DEF 为等边三角形,则∠α,∠β,∠γ之间的关系为 ( )
A.2∠β=∠α+∠γ B.2∠α=∠β+∠γ
C.2∠β=∠α-∠γ D.2∠α=∠β-∠γ
6如图,P 是等边△ABC 的边 BC 上任意一点,PE⊥AB,PF⊥AC,点 E,F为垂足,则∠EPF=
7[2024江西吉安期末]如图,△ABC是等边三角形,AD平分∠BAC,点 P 是射线AD 上一点,当△ABP 是等腰三角形时,∠CBP= .
8[2023 广东佛山南海区调研]如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,E,F分别为垂足,△DEF是等边三角形.
(1)求∠A的度数;
(2)求证:EF∥BC.
课时2 等边三角形的性质
刷基础
1. D 【解析】∵ BD,CE 分别为AC,AB 边上的高, 又·. AC, ,故A 选项不符合题意.∵ BD,CE 分别为 AC,AB 边上的中线, ∴ 在 和 中,
故B选项不符合题意.
∴在 和
中
(ASA),∴BD=CE,故C选项不符合题意.由 不能得出 故D 选项符合题意,故选 D.
2.【证明】· 是等腰三角形,AD是底边上的中线,. AB,∴ ∠AED = ∠AFD = 90°. 在 △AFD 和△AED中,
∴△AFD≌△AED,∴AE=AF.
3. C 【解析】连接BC.由题意可得OB=OC,OB=BC,即OB=OC=BC,∴△OBC 是等边三角形,∴∠O=60°.故选 C.
4. C 【解析】如图所示.∵△ABC为等边三角形,∴ ∠A = 60°. ∵ ∠1 是△AEF 的 一 个 外 角,∠1=140°,∴ ∠1=∠A+∠AEF,∴∠AEF=∠1-∠A=140°-60°=80°,∴ ∠DEB = ∠AEF = 80°. ∵ 直线 m∥n,∴∠DEB+∠2=180°,∴∠2=180°-∠DEB=180°-80°=100°.故选 C.
5. B 【解析】如图,∵AB=AC,∴ ∠B=∠C,∴ ∠2+∠γ=∠1+∠α,∴ ∠2-∠1=∠α-∠γ.∵ △DEF 是等边三角形,∴∠4=∠3=60°,∴∠2+∠α=∠1+∠β=120°,∴ ∠2-∠1=∠β-∠α,∴ ∠α-∠γ=∠β-∠α,∴2∠α=∠β+∠γ.故选 B.
6.120° 【解析】∵△ABC 是等边三角形,∴∠B=∠C=60°. ∵PE⊥AB,PF⊥AC,∴ ∠PEB=∠PFC=90°,∴∠EPB=∠FPC=180°-90°-60°=30°,∴ ∠EPF=180°-30°-30°=120°.
7.15°或30°或60° 【解析】如图(1),当AB=AP时,∵△ABC 是等边三角形,AD 平分∠BAC, 又∵AP⊥BC,∴∠PDB=90°,∴∠CBP=15°.如图(2),当BA=BP时,∵△ABC是等边三角形,AD平分 AP⊥BC.∵ BA=BP,∴ ∠BAP=∠BPA=30°.又∵AP⊥BC,∴∠PDB=90°,∴∠CBP=60°.如图(3),当PA=PB时,∵△ABC是等边三角形,AD 平分 ∠ABC=60°.∵ PA=PB,∴∠PBA=∠PAB=30°.又∵∠ABC=60°,∴∠CBP=30°.综上所述,∠CBP的度数为15°或30°或60°.
8.(1)【解】∵△DEF 是等边三角形,∴∠DEF=∠DFE=∠EDF=60°,DE=DF.∵ DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,∴∠AEF=∠AFE=180°-90°-60°=30°,∴ ∠A=180°-(∠AEF+∠AFE)=120°.
(2)【证明】∵ D 是BC的中点,∴BD=CD.在Rt△BED 和Rt△CFD 中,DE=DF,BD=CD, 即 BE = CF,∴△BED≌△CFD(SSS),∴ ∠B =∠C,则 ∴EF∥BC.
刷基础
知识点1 等腰三角形中的相等线段
1[2023山西晋中调研]如图,在△ABC中,AB=AC,给出的下列条件中,不能使BD=CE的是( )
A. BD,CE 分别为AC,AB 边上的高
B. BD,CE 分别为AC,AB 边上的中线
D.∠ABD=∠BCE
2[2024上海宝山区期末]已知:如图,△ABC 是等腰三角形,AD 是底边上的中线,DE 和 DF分别垂直于 AB,AC,垂足分别为点 E,F.求证:AE=AF.
知识点2 等边三角形的性质
3如图,以O为圆心,任意长为半径画弧,与射线OA交于点 B,再以 B为圆心,BO 长为半径画弧,两弧交于点 C,画射线OC,则∠O 的度数为( )
A.30° B.45° C.60° D.75°
4[2024四川成都二模]如图,直线m∥n,△ABC是等边三角形,顶点 B 在直线n上,直线m交AB于点E,交AC于点 F,若∠1=140°,则∠2的度数是 ( )
A.110° B.105° C.100° D.95°
5如图,△ABC 中,AB=AC,△DEF 为等边三角形,则∠α,∠β,∠γ之间的关系为 ( )
A.2∠β=∠α+∠γ B.2∠α=∠β+∠γ
C.2∠β=∠α-∠γ D.2∠α=∠β-∠γ
6如图,P 是等边△ABC 的边 BC 上任意一点,PE⊥AB,PF⊥AC,点 E,F为垂足,则∠EPF=
7[2024江西吉安期末]如图,△ABC是等边三角形,AD平分∠BAC,点 P 是射线AD 上一点,当△ABP 是等腰三角形时,∠CBP= .
8[2023 广东佛山南海区调研]如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,E,F分别为垂足,△DEF是等边三角形.
(1)求∠A的度数;
(2)求证:EF∥BC.
课时2 等边三角形的性质
刷基础
1. D 【解析】∵ BD,CE 分别为AC,AB 边上的高, 又·. AC, ,故A 选项不符合题意.∵ BD,CE 分别为 AC,AB 边上的中线, ∴ 在 和 中,
故B选项不符合题意.
∴在 和
中
(ASA),∴BD=CE,故C选项不符合题意.由 不能得出 故D 选项符合题意,故选 D.
2.【证明】· 是等腰三角形,AD是底边上的中线,. AB,∴ ∠AED = ∠AFD = 90°. 在 △AFD 和△AED中,
∴△AFD≌△AED,∴AE=AF.
3. C 【解析】连接BC.由题意可得OB=OC,OB=BC,即OB=OC=BC,∴△OBC 是等边三角形,∴∠O=60°.故选 C.
4. C 【解析】如图所示.∵△ABC为等边三角形,∴ ∠A = 60°. ∵ ∠1 是△AEF 的 一 个 外 角,∠1=140°,∴ ∠1=∠A+∠AEF,∴∠AEF=∠1-∠A=140°-60°=80°,∴ ∠DEB = ∠AEF = 80°. ∵ 直线 m∥n,∴∠DEB+∠2=180°,∴∠2=180°-∠DEB=180°-80°=100°.故选 C.
5. B 【解析】如图,∵AB=AC,∴ ∠B=∠C,∴ ∠2+∠γ=∠1+∠α,∴ ∠2-∠1=∠α-∠γ.∵ △DEF 是等边三角形,∴∠4=∠3=60°,∴∠2+∠α=∠1+∠β=120°,∴ ∠2-∠1=∠β-∠α,∴ ∠α-∠γ=∠β-∠α,∴2∠α=∠β+∠γ.故选 B.
6.120° 【解析】∵△ABC 是等边三角形,∴∠B=∠C=60°. ∵PE⊥AB,PF⊥AC,∴ ∠PEB=∠PFC=90°,∴∠EPB=∠FPC=180°-90°-60°=30°,∴ ∠EPF=180°-30°-30°=120°.
7.15°或30°或60° 【解析】如图(1),当AB=AP时,∵△ABC 是等边三角形,AD 平分∠BAC, 又∵AP⊥BC,∴∠PDB=90°,∴∠CBP=15°.如图(2),当BA=BP时,∵△ABC是等边三角形,AD平分 AP⊥BC.∵ BA=BP,∴ ∠BAP=∠BPA=30°.又∵AP⊥BC,∴∠PDB=90°,∴∠CBP=60°.如图(3),当PA=PB时,∵△ABC是等边三角形,AD 平分 ∠ABC=60°.∵ PA=PB,∴∠PBA=∠PAB=30°.又∵∠ABC=60°,∴∠CBP=30°.综上所述,∠CBP的度数为15°或30°或60°.
8.(1)【解】∵△DEF 是等边三角形,∴∠DEF=∠DFE=∠EDF=60°,DE=DF.∵ DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,∴∠AEF=∠AFE=180°-90°-60°=30°,∴ ∠A=180°-(∠AEF+∠AFE)=120°.
(2)【证明】∵ D 是BC的中点,∴BD=CD.在Rt△BED 和Rt△CFD 中,DE=DF,BD=CD, 即 BE = CF,∴△BED≌△CFD(SSS),∴ ∠B =∠C,则 ∴EF∥BC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
