第二章 二次函数 单元培优练(含答案)北师大版数学九年级下册
文档属性
| 名称 | 第二章 二次函数 单元培优练(含答案)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览



文档简介
北师大版九年级下册数学 第二章 二次函数
单元培优练
一、选择题
1.二次函数y=x(x+2)图象的对称轴是( )
A.x=﹣1 B.x=﹣2 C.x=2 D.y轴
2.下列关于二次函数y=2x2的说法正确的是( )
A.它的图象经过点(-1,-2)
B.它的图象的对称轴是直线x=2
C.当x<0时,y随x的增大而增大
D.当-12时,y有最大值为8,最小值为0
3.将抛物线向右平移a个单位,再向上平移b个单位得到解析式,则a、b的值是( )
A.1,-3 B.1,2 C.1,3 D.-2,-3
4.对于抛物线,下列判断错误的是( )
A.对称轴是直线 B.与x轴有两个交点
C.开口向上 D.与y轴在的交点在x轴下方
5.若抛物线 只经过三个象限,则a的取值范围是( )
A. B. C. D.
6.小明在研究抛物线(h为常数)时,得到如下结论,其中正确的是( )
A.无论x取何实数,y的值都小于0
B.该抛物线的顶点始终在直线上
C.当时,y随x的增大而增大,则
D.该抛物线上有两点,,若,,则
7.函数 的图象上有三个点分别为 , , ,则 , , 的大小关系为( )
A.
B.
C.
D. , , 的大小不确定
8.二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x … ﹣1 0 1 2 3 …
y=ax2+bx+c … p t n t 0 …
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
A.1m B.2m C.3m D.6m
10.如图,抛物线的顶点为.下列结论:(1);(2);(3)若关于x的方程有两个不相等的实数根,则;(4)若,且,则.其中正确的结论有( ).
A.1个 B.2个 C.3 D.4个
二、填空题
11.将抛物线y=-(x+1)2+3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为 .
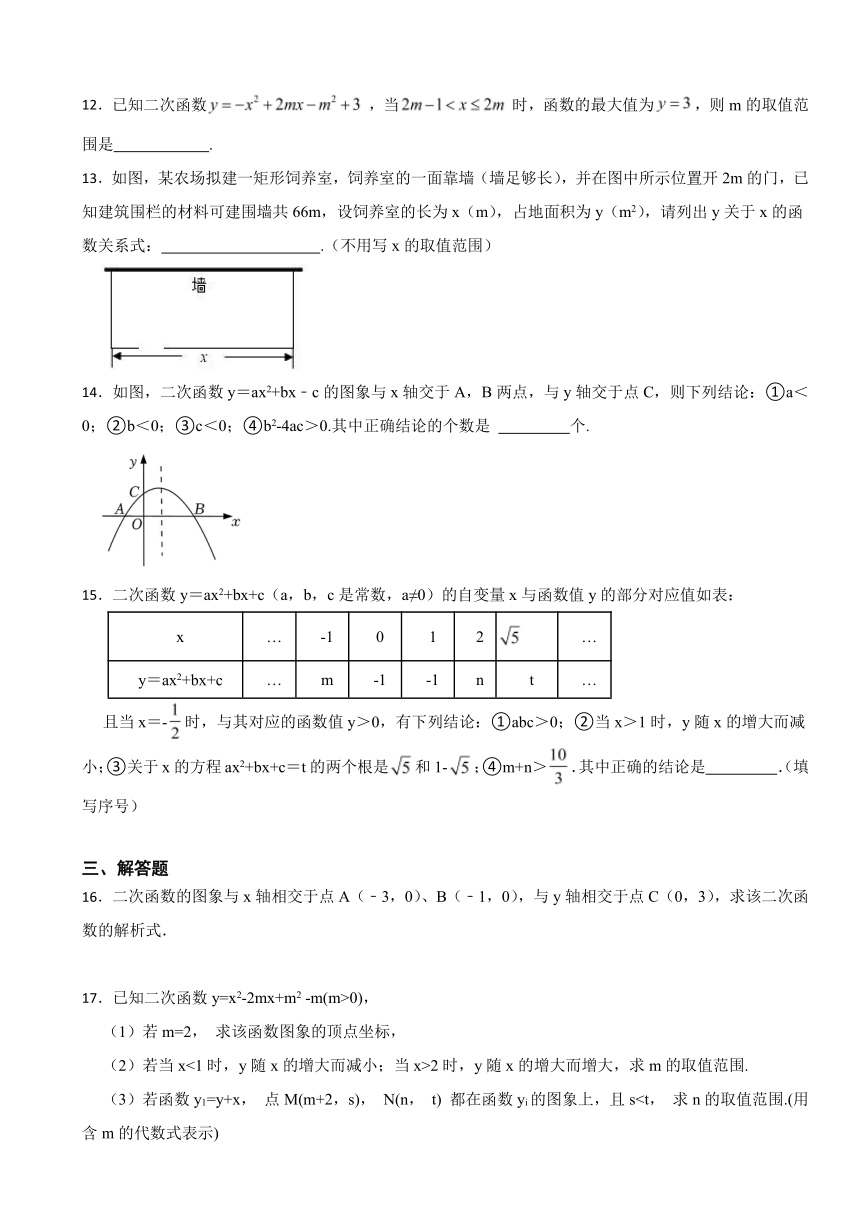
12.已知二次函数,当时,函数的最大值为,则m的取值范围是 .
13.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: .(不用写x的取值范围)
14.如图,二次函数y=ax2+bx﹣c的图象与x轴交于A,B两点,与y轴交于点C,则下列结论:①a<0;②b<0;③c<0;④b2-4ac>0.其中正确结论的个数是 个.
15.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
x … -1 0 1 2 …
y=ax2+bx+c … m -1 -1 n t …
且当x=-时,与其对应的函数值y>0,有下列结论:①abc>0;②当x>1时,y随x的增大而减小;③关于x的方程ax2+bx+c=t的两个根是和1-;④m+n>.其中正确的结论是 .(填写序号)
三、解答题
16.二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),求该二次函数的解析式.
17.已知二次函数y=x2-2mx+m2 -m(m>0),
(1)若m=2, 求该函数图象的顶点坐标,
(2)若当x<1时,y随x的增大而减小;当x>2时,y随x的增大而增大,求m的取值范围.
(3)若函数y1=y+x, 点M(m+2,s), N(n, t) 都在函数yi的图象上,且s18.“味香园”葡萄基地是宁波市最大的葡萄生产基地,“味香园”葡萄以品种多,质量好而声名远播.某“味香园”农户准备将“巨峰”和“美人指”两种葡萄装箱销售,推出了两种方案:2千克“巨峰”和3千克“美人指”装一箱按批发价每箱98元;3千克“巨峰”和2千克“美人指”装一箱按批发价每箱92元.
(1)求“巨峰”和“美人指”两种葡萄批发价每千克分别是多少元?
(2)某经销商在“味香园”按批发价购入一批“巨峰”葡萄进行销售,经调查发现:当销售价为每千克24元进行销售时,每天能卖出80千克;销售单价每降价0.2元,每天能多卖出4千克.求销售价定为每千克多少元时,每天的利润最大,最大利润是多少元?
19. 如图,地面上两根等长立柱,之间悬挂一根近似成抛物线的绳子.解答下列问题:
(1)两根等长立柱,的高度是 ▲ 米;并求出绳子最低点离地面的距离.
(2)因实际需要,在离为3米的位置处用一根立柱撑起绳子如图2),使左边抛物线的最低点距为米,离地面2米,求的长.
(3)将立柱的长度提升为3米,通过调整的位置,使抛物线对应函数的二次项系数始终为,设离的距离为米,抛物线的顶点离地面距离为米,当时,求的取值范围.
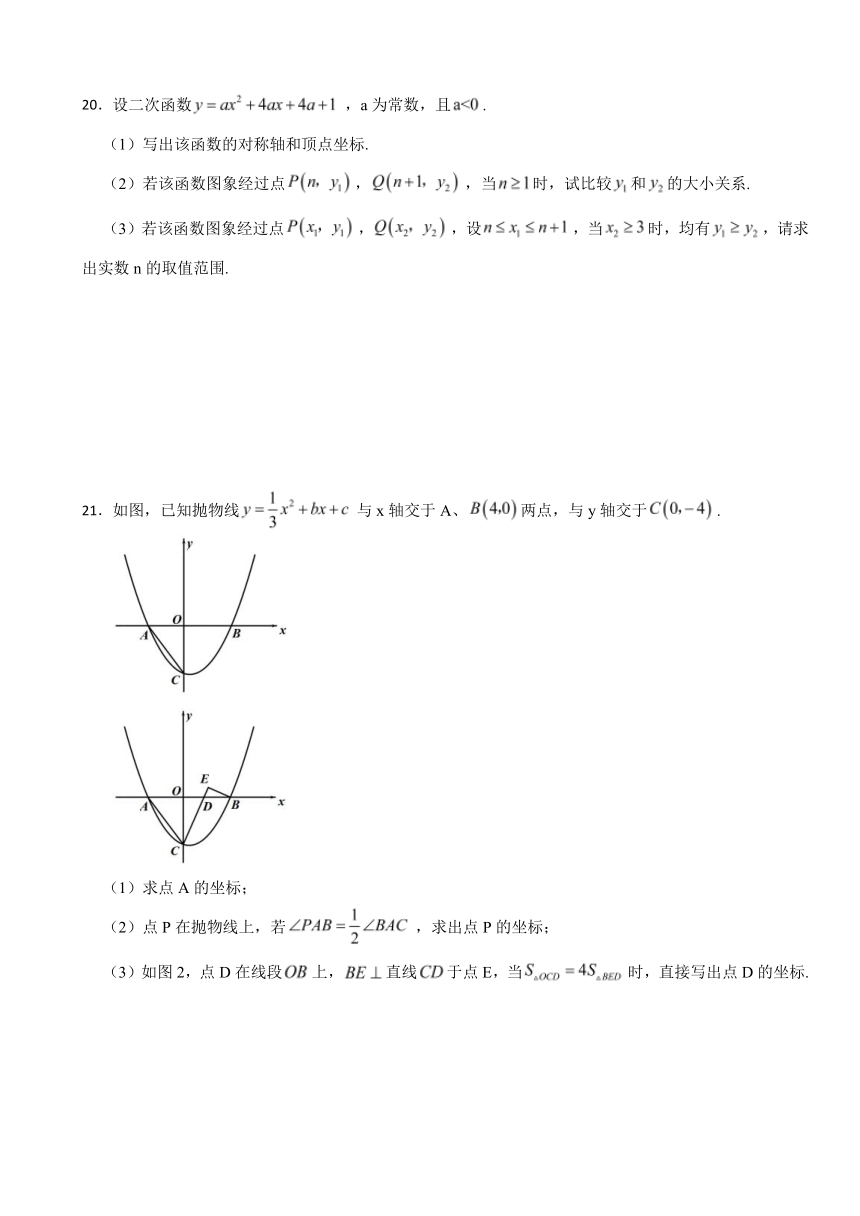
20.设二次函数,a为常数,且.
(1)写出该函数的对称轴和顶点坐标.
(2)若该函数图象经过点,,当时,试比较和的大小关系.
(3)若该函数图象经过点,,设,当时,均有,请求出实数n的取值范围.
21.如图,已知抛物线与x轴交于A、两点,与y轴交于.
(1)求点A的坐标;
(2)点P在抛物线上,若,求出点P的坐标;
(3)如图2,点D在线段上,直线于点E,当时,直接写出点D的坐标.
参考答案
1.A 2.D 3.A 4.A 5.C 6.C 7.B 8.C 9.B 10.A
11.y=-(x-1)2+5
12.0≤m<1
13.y=﹣ x2+34x
14.2
15.①③④
16.解:依题意:可设所求解析式为:y=a(x+1)(x+3)把点C(0,3)代入,
解得:a=1,
所求解析式为:y=x2+4x+3
17.(1)解:
当m=2时,顶点坐标为(2,-2).
(2)解:∵y=(x-m)2-m,
∴当x<m时y随x的增大而增大,当x>m时y随x的增大而减小,
∵当x<1时,y随x的增大而减小;当x>2时,y随x的增大而增大,
∴m的取值范围为1≤m≤2
(3) ,
因为M,N都在函数 的图象上,
所以 ,即 ,
,
因为s所以 < ,
所以 ,所以 或 ,即 或 .
18.(1)解:设“巨峰”批发价每千克x元,“美人指”批发价每千克y元,
由题意可得:,
解得:,
∴“巨峰”批发价每千克16元,“美人指”批发价每千克22元;
(2) 解:设销售价定为每千克a元,每天的利润为w元,
由题意可得:,
∵,
∴的图象开口向下,
∴当a=22时,即销售价为每千克22元时,w最大,且为720元.
19.(1)解:3;,
抛物线顶点为最低点,
,
绳子最低点离地面的距离为:米;
(2)解:由(1)可知,对称轴为,则,
令得,
,,
由题意可得:抛物线的顶点坐标为:,
设的解析式为:,
将代入得:,
解得:,
抛物线为:,
当时,,
的长度为:米;
(3)解:,
根据抛物线的对称性可知抛物线的顶点在的垂直平分线上,
的横坐标为:,
抛物线的顶点坐标为:,
抛物线的解析式为:,
把代入得:,
解得:,
,
是关于的二次函数,
又由已知,在对称轴的左侧,
随的增大而增大,
当时,,
解得:,不符合题意,舍去,
当时,,
解得:,不符合题意,舍去,
的取值范围是:.
20.(1)解:,
∴该函数的对称轴为直线,顶点坐标为
(2)解:∵,对称轴为直线,
∴当时,y随x的增大而减小,
∵该函数图象经过点,,且,
∴当时,
(3)解:∵,对称轴为直线,且当时,均有,
∴,
则或,
∴或,
∵,
∴,
∵该函数图象经过点,,设,当时,均有,
∴,则.
21.(1)解:将,代入中,
,
解得:,
,
当时,,
解得:,
;
(2)解:,
当时,;
,
过点A作的角平分线交于y轴于F,
过点F作垂直交于G,如下图:
,
设,则,
,
即,
解得:,
,
,
,
当点P到第一象限中,
,
解得:(舍去),
,
,
当点P到第四象限中,
,
解得:(舍去),
,
,
故若,点P的坐标为或;
(3)
单元培优练
一、选择题
1.二次函数y=x(x+2)图象的对称轴是( )
A.x=﹣1 B.x=﹣2 C.x=2 D.y轴
2.下列关于二次函数y=2x2的说法正确的是( )
A.它的图象经过点(-1,-2)
B.它的图象的对称轴是直线x=2
C.当x<0时,y随x的增大而增大
D.当-12时,y有最大值为8,最小值为0
3.将抛物线向右平移a个单位,再向上平移b个单位得到解析式,则a、b的值是( )
A.1,-3 B.1,2 C.1,3 D.-2,-3
4.对于抛物线,下列判断错误的是( )
A.对称轴是直线 B.与x轴有两个交点
C.开口向上 D.与y轴在的交点在x轴下方
5.若抛物线 只经过三个象限,则a的取值范围是( )
A. B. C. D.
6.小明在研究抛物线(h为常数)时,得到如下结论,其中正确的是( )
A.无论x取何实数,y的值都小于0
B.该抛物线的顶点始终在直线上
C.当时,y随x的增大而增大,则
D.该抛物线上有两点,,若,,则
7.函数 的图象上有三个点分别为 , , ,则 , , 的大小关系为( )
A.
B.
C.
D. , , 的大小不确定
8.二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x … ﹣1 0 1 2 3 …
y=ax2+bx+c … p t n t 0 …
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
A.1m B.2m C.3m D.6m
10.如图,抛物线的顶点为.下列结论:(1);(2);(3)若关于x的方程有两个不相等的实数根,则;(4)若,且,则.其中正确的结论有( ).
A.1个 B.2个 C.3 D.4个
二、填空题
11.将抛物线y=-(x+1)2+3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为 .
12.已知二次函数,当时,函数的最大值为,则m的取值范围是 .
13.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: .(不用写x的取值范围)
14.如图,二次函数y=ax2+bx﹣c的图象与x轴交于A,B两点,与y轴交于点C,则下列结论:①a<0;②b<0;③c<0;④b2-4ac>0.其中正确结论的个数是 个.
15.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
x … -1 0 1 2 …
y=ax2+bx+c … m -1 -1 n t …
且当x=-时,与其对应的函数值y>0,有下列结论:①abc>0;②当x>1时,y随x的增大而减小;③关于x的方程ax2+bx+c=t的两个根是和1-;④m+n>.其中正确的结论是 .(填写序号)
三、解答题
16.二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),求该二次函数的解析式.
17.已知二次函数y=x2-2mx+m2 -m(m>0),
(1)若m=2, 求该函数图象的顶点坐标,
(2)若当x<1时,y随x的增大而减小;当x>2时,y随x的增大而增大,求m的取值范围.
(3)若函数y1=y+x, 点M(m+2,s), N(n, t) 都在函数yi的图象上,且s
(1)求“巨峰”和“美人指”两种葡萄批发价每千克分别是多少元?
(2)某经销商在“味香园”按批发价购入一批“巨峰”葡萄进行销售,经调查发现:当销售价为每千克24元进行销售时,每天能卖出80千克;销售单价每降价0.2元,每天能多卖出4千克.求销售价定为每千克多少元时,每天的利润最大,最大利润是多少元?
19. 如图,地面上两根等长立柱,之间悬挂一根近似成抛物线的绳子.解答下列问题:
(1)两根等长立柱,的高度是 ▲ 米;并求出绳子最低点离地面的距离.
(2)因实际需要,在离为3米的位置处用一根立柱撑起绳子如图2),使左边抛物线的最低点距为米,离地面2米,求的长.
(3)将立柱的长度提升为3米,通过调整的位置,使抛物线对应函数的二次项系数始终为,设离的距离为米,抛物线的顶点离地面距离为米,当时,求的取值范围.
20.设二次函数,a为常数,且.
(1)写出该函数的对称轴和顶点坐标.
(2)若该函数图象经过点,,当时,试比较和的大小关系.
(3)若该函数图象经过点,,设,当时,均有,请求出实数n的取值范围.
21.如图,已知抛物线与x轴交于A、两点,与y轴交于.
(1)求点A的坐标;
(2)点P在抛物线上,若,求出点P的坐标;
(3)如图2,点D在线段上,直线于点E,当时,直接写出点D的坐标.
参考答案
1.A 2.D 3.A 4.A 5.C 6.C 7.B 8.C 9.B 10.A
11.y=-(x-1)2+5
12.0≤m<1
13.y=﹣ x2+34x
14.2
15.①③④
16.解:依题意:可设所求解析式为:y=a(x+1)(x+3)把点C(0,3)代入,
解得:a=1,
所求解析式为:y=x2+4x+3
17.(1)解:
当m=2时,顶点坐标为(2,-2).
(2)解:∵y=(x-m)2-m,
∴当x<m时y随x的增大而增大,当x>m时y随x的增大而减小,
∵当x<1时,y随x的增大而减小;当x>2时,y随x的增大而增大,
∴m的取值范围为1≤m≤2
(3) ,
因为M,N都在函数 的图象上,
所以 ,即 ,
,
因为s
所以 ,所以 或 ,即 或 .
18.(1)解:设“巨峰”批发价每千克x元,“美人指”批发价每千克y元,
由题意可得:,
解得:,
∴“巨峰”批发价每千克16元,“美人指”批发价每千克22元;
(2) 解:设销售价定为每千克a元,每天的利润为w元,
由题意可得:,
∵,
∴的图象开口向下,
∴当a=22时,即销售价为每千克22元时,w最大,且为720元.
19.(1)解:3;,
抛物线顶点为最低点,
,
绳子最低点离地面的距离为:米;
(2)解:由(1)可知,对称轴为,则,
令得,
,,
由题意可得:抛物线的顶点坐标为:,
设的解析式为:,
将代入得:,
解得:,
抛物线为:,
当时,,
的长度为:米;
(3)解:,
根据抛物线的对称性可知抛物线的顶点在的垂直平分线上,
的横坐标为:,
抛物线的顶点坐标为:,
抛物线的解析式为:,
把代入得:,
解得:,
,
是关于的二次函数,
又由已知,在对称轴的左侧,
随的增大而增大,
当时,,
解得:,不符合题意,舍去,
当时,,
解得:,不符合题意,舍去,
的取值范围是:.
20.(1)解:,
∴该函数的对称轴为直线,顶点坐标为
(2)解:∵,对称轴为直线,
∴当时,y随x的增大而减小,
∵该函数图象经过点,,且,
∴当时,
(3)解:∵,对称轴为直线,且当时,均有,
∴,
则或,
∴或,
∵,
∴,
∵该函数图象经过点,,设,当时,均有,
∴,则.
21.(1)解:将,代入中,
,
解得:,
,
当时,,
解得:,
;
(2)解:,
当时,;
,
过点A作的角平分线交于y轴于F,
过点F作垂直交于G,如下图:
,
设,则,
,
即,
解得:,
,
,
,
当点P到第一象限中,
,
解得:(舍去),
,
,
当点P到第四象限中,
,
解得:(舍去),
,
,
故若,点P的坐标为或;
(3)
