苏科版八年级数学下第11章反比例函数期终复习试卷含答案
文档属性
| 名称 | 苏科版八年级数学下第11章反比例函数期终复习试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-07 15:44:18 | ||
图片预览



文档简介
八(下)第11章《反比例函数》考点练习
考点:反比例函数;反比例函数图像与性质;用反比例函数解决问题。
一、选择题:
1、已知函数y=﹣x+5,y=,它们的共同点是:①函数y随x的增大而减少;②都有部分图象在第一象限;③都经过点(1,4),其中错误的有( )
A.0个 B.1个 C.2个 D.3个
2、如图,A、B、C是反比例函数图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
A.4条 B.3条 C.2条 D.1条
3、某地资源总量Q一定,该地人均资源享有量与人口数的函数关系图象是( )
A. B. C. D.
4、为了更好保护水资源,造福人类,某工厂计 ( http: / / www.21cnjy.com )划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是
A. B. C. D.
(第2题)(第5题)
5、反比例函数的图象如图所示,则k的值可能是( )
A.﹣1 B. C.1 D.2
6、已知长方形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为图中的( )
A. B. C. D.
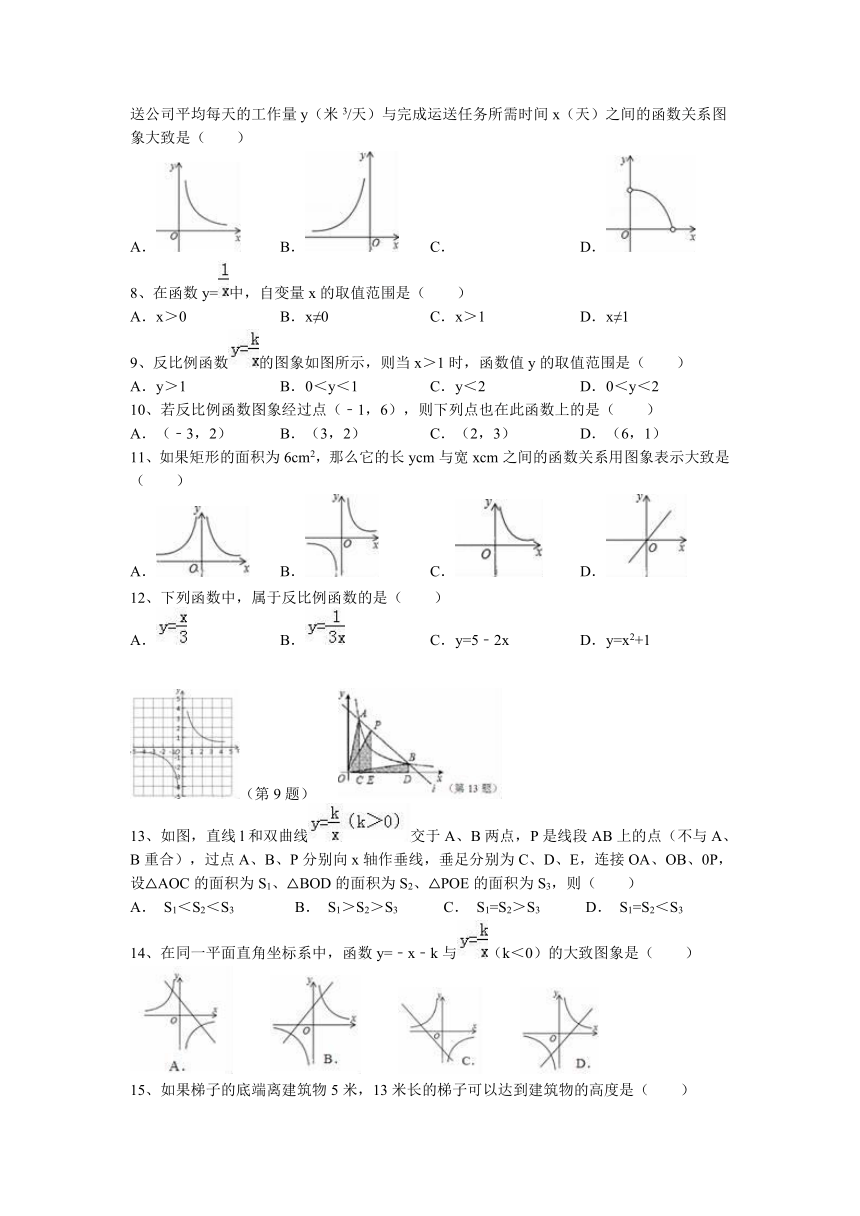
7、一项市政工程,需运送土石方106米3, ( http: / / www.21cnjy.com )某运输公司承办了这项运送土石方的工程,则运送公司平均每天的工作量y(米3/天)与完成运送任务所需时间x(天)之间的函数关系图象大致是( )
A. B. C. D.
8、在函数y=中,自变量x的取值范围是( )
A.x>0 B.x≠0 C.x>1 D.x≠1
9、反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
10、若反比例函数图象经过点(﹣1,6),则下列点也在此函数上的是( )
A.(﹣3,2) B.(3,2) C.(2,3) D.(6,1)
11、如果矩形的面积为6cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
A. B. C. D.
12、下列函数中,属于反比例函数的是( )
A. B. C.y=5﹣2x D.y=x2+1
(第9题)
13、如图,直线l和双曲线 ( http: / / www.21cnjy.com )交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
A. S1<S2<S3 B. S1>S2>S3 C. S1=S2>S3 D. S1=S2<S3
14、在同一平面直角坐标系中,函数y=﹣x﹣k与(k<0)的大致图象是( )
15、如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A. 12米 B. 13米 C.14米 D.15米
二、填空题:
16、在平面直角坐标系xOy中,一次函数与反比例函数的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .
17、直线y=-x+b与双曲线y=-(x<0)交于点A,与x轴交于点B,则OA2-OB2= .
(第17题)(第24题)
18、若函数是y关于x的反比例函数,则k= .
19、双曲线y=经过点(2,﹣3),则k= .
20、如果我们把横坐标与纵坐标均为整数的点称为整点,那么反比例函数在第四象限的图象上的整点个数共有 个.
21、已知某个反比例函数的图象经过点(3,6)和点(m,﹣2),则m的值是 .
22、反比例函数y=的图象经过点(﹣2,3),则k的值为 .
23、函数与y=x﹣2图象交点的横坐标分别为a,b,则的值为 .
24、两个反比例函数,在第一象限内 ( http: / / www.21cnjy.com )的图像如图所示,点,,,…,在函数的图像上,它们的横坐标分别是,,,…,,纵坐标分别是1,3,5,…,共2013个连续奇数,过点,,,…,分别作y轴的平行线,与函数的图像交点依次是(,),(,),(,),…,(,),则 .
25、反比例函数的图象经过点(1,2),则k= 。
三、计算题:
26、如图,是反比例函数的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
27、已知一次函数的图象与反比例函数图象交于点 P(4,n)。求P点坐标
28、如图,矩形的对角线经过坐标原点,矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为,则的值为 .
( http: / / www.21cnjy.com )
29、、(2011 綦江县)如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=﹣的图象的交点.
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.
30、已知直线与双曲线交于点P().
(1)求m的值;
(2)若点、在双曲线上.且,试比较的大小.
四、解答题:
31、已知:点O是平面直角坐标系的 ( http: / / www.21cnjy.com )原点,如直线y=﹣x+m+n与双曲线交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
32、如图,正比例函数y1=x的图象与反比例函数(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
33、通过对苏科版八(下)教材一道习题的探索 ( http: / / www.21cnjy.com )研究,我们知道:一次函数y=x﹣1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数的图象是由反比例函数的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
如图,已知反比例函数的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
(1)写出点B的坐标,并求a的值;
(2)将函数的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
①求n的值;②分别写出平移后的两个图象C′和l′对应的函数关系式;③直接写出不等式的解集.
34、如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.
35、如图,直线y=k1x+b(k1≠0)与双曲线(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1) ( http: / / www.21cnjy.com ),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
参考答案
1.B;2.A;3.B;4.C;5.B;6.A;7.A;8.B;9.D;10.A;11.C;12.B;13.D;14.A;15.A;16.1;17.2;18.2;19.-6;20.2;21.-9;22.﹣6;23.-2;24.;25.2;26.(1)函数图象位于第二、四象限,m<5。(2)①当y1<y2<0时,x1<x2;②当0<y1<y2,x1<x2。27.P(4,2);28.;29.:解:(1)将A (4,a),B (﹣2,﹣4)两点坐标代入y=﹣中,得4a=(﹣2)×(﹣4)=m,解得a=2,m=8,将A(4,2),B(﹣2,﹣4)代入y=kx+b中,得,解得,∴反比例函数解析式为y=,一次函数的解祈式为y=x﹣2;
(2)设直线AB交y轴于C点,由直线AB的解析式y=x﹣2得C(0,﹣2),
∴S△AOB=S△AOC+S△BOC=×2×4+×2×2=6.
( http: / / www.21cnjy.com )
30.
31.<S≤;32.(1);(2点B的坐标为(﹣2,﹣2)。﹣2<x<0或x>2。
33.(1)∴B点坐标为(﹣2,﹣2)。a=1。(2)①n=1。
②; y=x﹣1。③x≥3或﹣1≤x<1。
34.(1)y= (2)存在.
35.(1)k2=2 ;(2)y2<y1<y3。
考点:反比例函数;反比例函数图像与性质;用反比例函数解决问题。
一、选择题:
1、已知函数y=﹣x+5,y=,它们的共同点是:①函数y随x的增大而减少;②都有部分图象在第一象限;③都经过点(1,4),其中错误的有( )
A.0个 B.1个 C.2个 D.3个
2、如图,A、B、C是反比例函数图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
A.4条 B.3条 C.2条 D.1条
3、某地资源总量Q一定,该地人均资源享有量与人口数的函数关系图象是( )
A. B. C. D.
4、为了更好保护水资源,造福人类,某工厂计 ( http: / / www.21cnjy.com )划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是
A. B. C. D.
(第2题)(第5题)
5、反比例函数的图象如图所示,则k的值可能是( )
A.﹣1 B. C.1 D.2
6、已知长方形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为图中的( )
A. B. C. D.
7、一项市政工程,需运送土石方106米3, ( http: / / www.21cnjy.com )某运输公司承办了这项运送土石方的工程,则运送公司平均每天的工作量y(米3/天)与完成运送任务所需时间x(天)之间的函数关系图象大致是( )
A. B. C. D.
8、在函数y=中,自变量x的取值范围是( )
A.x>0 B.x≠0 C.x>1 D.x≠1
9、反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
10、若反比例函数图象经过点(﹣1,6),则下列点也在此函数上的是( )
A.(﹣3,2) B.(3,2) C.(2,3) D.(6,1)
11、如果矩形的面积为6cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
A. B. C. D.
12、下列函数中,属于反比例函数的是( )
A. B. C.y=5﹣2x D.y=x2+1
(第9题)
13、如图,直线l和双曲线 ( http: / / www.21cnjy.com )交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
A. S1<S2<S3 B. S1>S2>S3 C. S1=S2>S3 D. S1=S2<S3
14、在同一平面直角坐标系中,函数y=﹣x﹣k与(k<0)的大致图象是( )
15、如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A. 12米 B. 13米 C.14米 D.15米
二、填空题:
16、在平面直角坐标系xOy中,一次函数与反比例函数的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .
17、直线y=-x+b与双曲线y=-(x<0)交于点A,与x轴交于点B,则OA2-OB2= .
(第17题)(第24题)
18、若函数是y关于x的反比例函数,则k= .
19、双曲线y=经过点(2,﹣3),则k= .
20、如果我们把横坐标与纵坐标均为整数的点称为整点,那么反比例函数在第四象限的图象上的整点个数共有 个.
21、已知某个反比例函数的图象经过点(3,6)和点(m,﹣2),则m的值是 .
22、反比例函数y=的图象经过点(﹣2,3),则k的值为 .
23、函数与y=x﹣2图象交点的横坐标分别为a,b,则的值为 .
24、两个反比例函数,在第一象限内 ( http: / / www.21cnjy.com )的图像如图所示,点,,,…,在函数的图像上,它们的横坐标分别是,,,…,,纵坐标分别是1,3,5,…,共2013个连续奇数,过点,,,…,分别作y轴的平行线,与函数的图像交点依次是(,),(,),(,),…,(,),则 .
25、反比例函数的图象经过点(1,2),则k= 。
三、计算题:
26、如图,是反比例函数的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
27、已知一次函数的图象与反比例函数图象交于点 P(4,n)。求P点坐标
28、如图,矩形的对角线经过坐标原点,矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为,则的值为 .
( http: / / www.21cnjy.com )
29、、(2011 綦江县)如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=﹣的图象的交点.
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.
30、已知直线与双曲线交于点P().
(1)求m的值;
(2)若点、在双曲线上.且,试比较的大小.
四、解答题:
31、已知:点O是平面直角坐标系的 ( http: / / www.21cnjy.com )原点,如直线y=﹣x+m+n与双曲线交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
32、如图,正比例函数y1=x的图象与反比例函数(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
33、通过对苏科版八(下)教材一道习题的探索 ( http: / / www.21cnjy.com )研究,我们知道:一次函数y=x﹣1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数的图象是由反比例函数的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
如图,已知反比例函数的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
(1)写出点B的坐标,并求a的值;
(2)将函数的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
①求n的值;②分别写出平移后的两个图象C′和l′对应的函数关系式;③直接写出不等式的解集.
34、如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.
35、如图,直线y=k1x+b(k1≠0)与双曲线(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1) ( http: / / www.21cnjy.com ),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
参考答案
1.B;2.A;3.B;4.C;5.B;6.A;7.A;8.B;9.D;10.A;11.C;12.B;13.D;14.A;15.A;16.1;17.2;18.2;19.-6;20.2;21.-9;22.﹣6;23.-2;24.;25.2;26.(1)函数图象位于第二、四象限,m<5。(2)①当y1<y2<0时,x1<x2;②当0<y1<y2,x1<x2。27.P(4,2);28.;29.:解:(1)将A (4,a),B (﹣2,﹣4)两点坐标代入y=﹣中,得4a=(﹣2)×(﹣4)=m,解得a=2,m=8,将A(4,2),B(﹣2,﹣4)代入y=kx+b中,得,解得,∴反比例函数解析式为y=,一次函数的解祈式为y=x﹣2;
(2)设直线AB交y轴于C点,由直线AB的解析式y=x﹣2得C(0,﹣2),
∴S△AOB=S△AOC+S△BOC=×2×4+×2×2=6.
( http: / / www.21cnjy.com )
30.
31.<S≤;32.(1);(2点B的坐标为(﹣2,﹣2)。﹣2<x<0或x>2。
33.(1)∴B点坐标为(﹣2,﹣2)。a=1。(2)①n=1。
②; y=x﹣1。③x≥3或﹣1≤x<1。
34.(1)y= (2)存在.
35.(1)k2=2 ;(2)y2<y1<y3。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
