期末测试卷(含答案)---2024-2025学年五年级数学下册(西师大版)
文档属性
| 名称 | 期末测试卷(含答案)---2024-2025学年五年级数学下册(西师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 07:34:40 | ||
图片预览




文档简介
保密★启用前
2024-2025学年五年级下册期末测试卷(西师大版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.杭州市2月份的气温变化莫测。小冬想知道杭州市2023年2月份的气温变化趋势,应该搜集的数据是( )
A.2023年各季度的平均气温 B.2023年各月的平均气温
C.2023年2月1日各时刻的气温 D.2023年2月份每天的平均气温
2.下列选项中,解决问题与体积有关的是( )。
A.包装一份生日礼物需要多少彩纸
B.给一个玻璃柜台各边装上角铁,需要多少角铁
C.油漆大厅里的柱子,需要多少油漆
D.一个玻璃球沉入装满水的杯子中,溢出多少水
3. 的分子加上10,要使分数的大小不变,分母应( )
A.加上24 B.乘2 C.加上10 D.除以2
4.如下图,甲、乙是用若干个同样大小的小正方体搭成的立体图形。比较甲、乙的表面积,下面说法正确的是( )。
A.S甲>S乙 B.S甲5.一个等腰三角形两条边的长度分别是m和m,这个三角形周长是( )。
A.m B.2m C.m或2m D.不能确定
6.下列数线上有A、B两点,不在A、B两点之间的分数是( )。
A. B. C. D.
7.下列各组数中,都是质数的是( )。
A.1、3和7 B.2、5和29 C.39、49和57 D.11、17和21
8.下图是一块长方形纸板,从四个角各切掉一个边长为5cm的正方形,然后做成一个无盖的盒子,这个盒子的占地面积是( )cm2。
A.500 B.200 C.1000 D.300
9.一杯豆浆,小红喝了杯后,觉得有点甜,兑满了热水。又喝了半杯,她一共喝了( )杯豆浆。
A. B. C. D.
10.如果将一个长方体的长、宽、高都扩大2倍,那么它的体积将扩大( )倍。
A.2 B.4 C.6 D.8
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.如一个物体的体积为8立方厘米,则这个物体有可能是一块橡皮。( )
12.真分数都比1小,假分数都比1大。( )
13.体积相等的两个长方体,表面积也相等。( )
14.兰兰同学“六一”儿童节拍了40张照片,其中有24张是她喜欢的。她不喜欢的照片占所拍照片的。( )
15.用三个数字4、0、2任意组成一个三位数,有些不一定是2和3的倍数。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个等腰三角形的两边长分别是 米和 米,这个三角形的周长是 米。
17.用27个棱长是2cm的小正方体拼成一个大正方体(如图1)。从这个拼成的大正方体上取出3个小正方体(如图2),剩下几何体的表面积比原来大正方体的表面积多 cm2。
18.最小的自然数是 ,最小的奇数是 ,最小的质数是 ,最小的合数是 .
19.小塘买了a元/瓶的饮料3瓶,b元/包的饼干3包,微信支付后,其余额显示18.90元。3a+3b表示 ;3(a+b)+18.90表示 。
20.如下图,把一根长2米且横截面是正方形的长方体木料截成3段,表面积增加了64dm2。原来这根木料体积是 m3,表面积是 m2。
21.一根绳子长5米,把它平均分成6段,每段是这根绳子的 ,每段长 米。
22.一个长方体,它的棱长总和是40dm,且长、宽、高都是质数,这个长方体的体积是 dm3。
23.两个非0自然数m、n,若m=n+1,则m和n的最大公因数是 ,最小公倍数是 。
24.张强制作一个灯笼,需要用铁丝做一个长12厘米,宽10厘米,高18厘米的长方体框架,这根铁丝的长度至少 厘米。(接头处忽略不计)
25.小明到超市买了一瓶1250毫升的饮料,相当于 升。存放饮料的展示柜体积是2.5立方米,相当于 立方分米。
阅卷人 四、计算题(20分)
得分
26.直接写出得数
0.23= 2.4-= 0.8++-0.8=
2.1÷0.3= 11.6y-9y= 1-=
27.解方程
①3.85+1.5x=6.1 ②3x-=1.25
阅卷人 五、操作题(10分)
得分
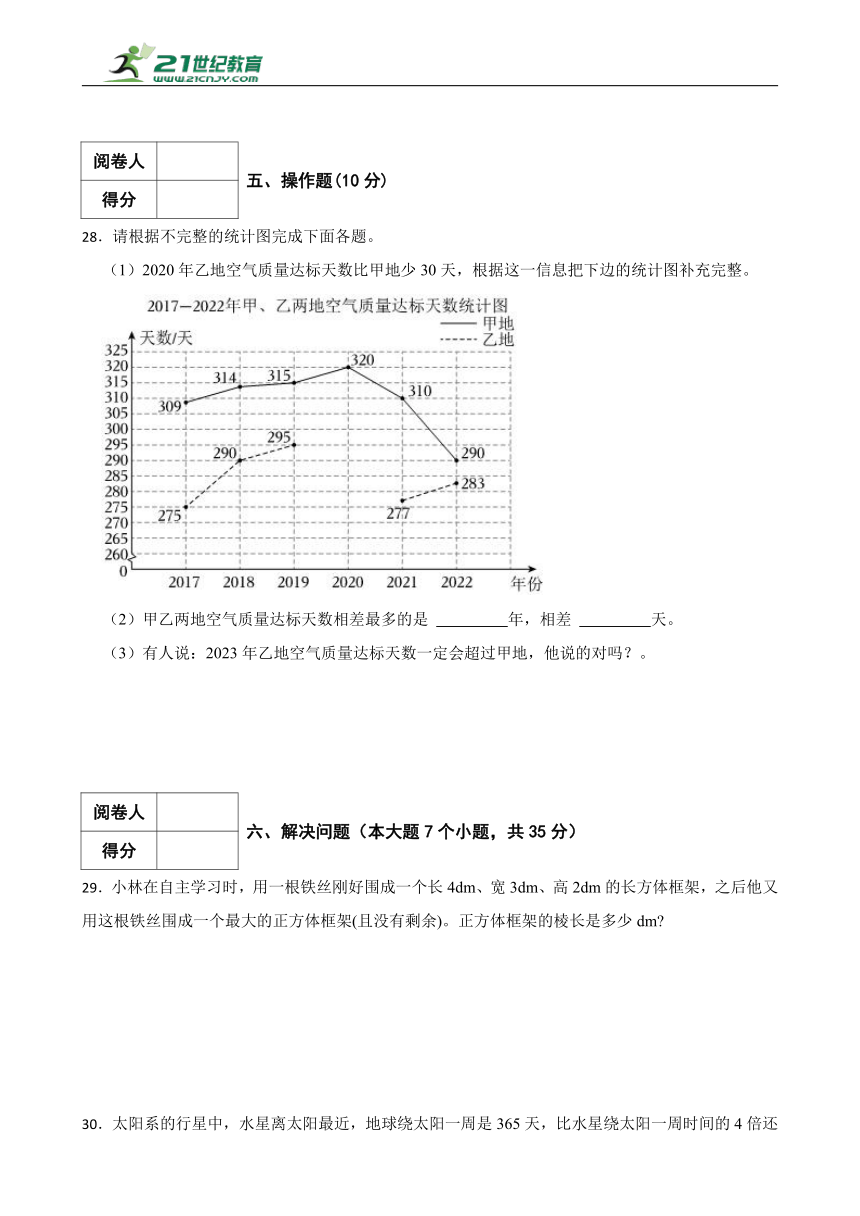
28.请根据不完整的统计图完成下面各题。
(1)2020年乙地空气质量达标天数比甲地少30天,根据这一信息把下边的统计图补充完整。
(2)甲乙两地空气质量达标天数相差最多的是 年,相差 天。
(3)有人说:2023年乙地空气质量达标天数一定会超过甲地,他说的对吗?。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.小林在自主学习时,用一根铁丝刚好围成一个长4dm、宽3dm、高2dm的长方体框架,之后他又用这根铁丝围成一个最大的正方体框架(且没有剩余)。正方体框架的棱长是多少dm
30.太阳系的行星中,水星离太阳最近,地球绕太阳一周是365天,比水星绕太阳一周时间的4倍还多13天,水星绕太阳一周是多少天?(列方程解答)
31.落实双减政策,某学校为了开设游泳课新建了一个游泳馆,长25米,宽11米,深2米。需要在游泳池的四周和底面铺上一层瓷砖,请问铺瓷砖的面积有多少平方米?
32.某小学六(2)班的学生分组进行植树活动,如果按8人一组,正好分完,如果按12人一组,也正好分完。这个班最少有多少名学生?
33.一块长方形铁皮,长96厘米,宽80厘米,要把它剪成同样大小的正方形且没有剩余,这种正方形的边长最长是多少?被剪成几块?
34.洒下绿色,播种希望,植树是我们和春天不变的约定。为了响应植树节的号召,某校五(1)班同学计划买树苗来种树,如果每人出8角,就多2元;如果每人出6角,就少6元,五(1)班有多少人?(列方程解答)
35.如下图所示,有一个无水的长方体水槽,一个水龙头从9:00开始向水槽内注水,水流速度为9dm3/分,9:04停止注水。接着在水槽内放入一个高为9厘米的长方体铁块,使其全部浸没在水中。从开始注水到铁块全部浸没在水中,水槽的水面高度变化情况如图中所示。
(1)9:04时,长方体水槽内水面高度是多少厘米?
(2)这个长方体铁块的底面积是多少平方厘米
答案解析部分
1.D
解:想知道杭州市2023年2月份的气温变化趋势,就要知道2023年2月份每天的平均气温。
故答案为:D。
先要收集出2023年2月份每天的平均气温,才能知道杭州市2023年2月份的气温变化趋势。
2.D
解:A项:求的是表面积;
B项:求的是棱长和;
C项:求的是表面积;
D项:求的是体积。
故答案为:D。
物体所占空间的大小,叫做物体的体积。所以一个玻璃球沉入装满水的杯子中,溢出多少水,其实就是求这个玻璃球的体积。
3.A
的分子加上10,5+10=15,15÷5=3,分子扩大3倍,要使分数的大小不变,分母应扩大3倍,12×3=36,增加36-12=24。
故答案为:A。
此题主要考查了分数的基本性质:分数的分子和分母同时乘或者除以相同的数(零除外),分数的大小不变,根据题意,先确定分子的变化情况,再确定分母的变化情况,据此解答。
4.B
解:甲的表面积=长方体的表面积,乙的表面积=长方体的表面积+小正方体2个面的面积;所以甲的表面积<乙的表面积。
故答案为:B。
物体表面的面积,叫做它的表面积,甲的表面积与长方体的表面积相等,乙的表面积比长方体的表面积大,所以甲的表面积<乙的表面积。
5.B
解:++
=+
=2(米)。
故答案为:B。
三角形任意两边之和大于第三边,任意两边之差小于第三边,所以这个等腰三角形的另一个条边长米,三角形的周长=三角形三条边的长度相加。
6.A
解:A项:=1÷4=0.25;
B项:=2÷3≈0.67;
C项:=5÷6≈0.83;
D项:=3÷2=1.5;
不在A、B两点之间。
故答案为:A。
分数化成小数,用分数的分子除以分母,A、B两点之间的数大约在0.5和1.6之间,则不在A、B两点之间。
7.B
A选项中“1”不是质数;B选项中都是质数;C选项中“49”不是质数;D选项中“21”不是质数。
故答案为:B
只有1和它本身两个因数的数,叫做质数;除了1和它本身以外还有其他因数的数叫做合数。据此判断即可。
8.B
解:(30-5×2)×(20-5×2)
=(30-10)×(20-10)
=20×10
=200(平方厘米)
故答案为:B。
30厘米-2个5厘米=长方体的长,20厘米-2个5厘米=长方体的宽,长方体的长×长方体的宽=这个盒子的占地面积。
9.A
解:+=,
她一共喝了杯豆浆。
故答案为:A。
第一次喝了杯;第二次兑满了热水。又喝了半杯豆浆的一半,是杯;第一次喝的杯数+第二次喝的杯数=她一共喝的杯数。
10.D
解:2×2×2=8,长方体的长、宽、高都扩大2倍,它的体积将扩大8倍。
故答案为:D。
长方体的体积=长×宽×高;三个因数扩大的倍数相乘,就是积扩大的倍数。
11.正确
解:如一个物体的体积为8立方厘米,则这个物体有可能是一块橡皮。说法正确。
故答案为:正确。
橡皮的长可能是4厘米,宽2厘米,高1厘米,符合实际情况。
12.错误
解:真分数都比1小,假分数大于或等于1。
故答案为:错误。
真分数小于1,假分数大于或等于1。
13.错误
解:举例说明:长、宽、高分别是3厘米、2厘米、1厘米的长方体;
体积是:3×2×1=6(立方厘米)
表面积是:3×2×2+3×1×2+2×1×2
=12+6+4
=22(平方厘米)
长、宽、高是1厘米、1厘米、6厘米的长方体;
体积是:1×1×6=6(立方厘米)
表面积是:1×1×2+1×6×2+1×6×2
=2+12+12
=26(平方厘米)
可见,体积相等的两个长方体,表面积不一定相等,原题说法错误。
故答案为:错误。
根据长方体的体积公式:V=abh以及长方体的表面积公式:S=a×b×2+a×h×2+b×h×2,可举例说明,当两个长方体的体积相等,它们的长、宽、高不一定相等,那么它们的表面积也不一定相等。
14.错误
解:(40-24)÷40
=16÷40
=
所以,她不喜欢的照片占所拍照片的,原题说法错误。
故答案为:错误。
根据求一个数占另一个数的几分之几是多少,用除法计算,用不喜欢的照片数量除以照片总数,结果用分数表示即可。
15.错误
解:因为4+0+2=6,6是3的倍数,所以用三个数字4、0、2任意组成一个三位数,一定是2和3的倍数;原题说法错误。
故答案为:错误。
3的倍数是各个数位上的数字之和能整除3的数;2的倍数是0、2、4、6、8结尾的整数。
16.
解:若米为腰长,+=,
因为<,所以米为腰长时不能围成三角形;
只能是米为腰长,
所以三角形的周长=++
=+
=+
=(米)。
故答案为:。
三角形的三边关系:三角形的两边之和大于第三边,三角形的两边之差小于第三边。
本题先判断出三角形的腰长,再将三边的长度相加即可得出答案。
17.16
解:(9-5)×(2×2)
=4×4
=16(平方厘米)。
故答案为:16。
剩下几何体的表面积比原来大正方体的表面积多了4个边长2cm正方形的面积。
18.0;1;2;4
最小的自然数是0,最小的奇数是1,最小的质数是2,最小的合数是4.
故答案为:0;1;2;4.
此题主要考查了自然数、奇数、质数、合数的认识,不能被2整除的数叫做奇数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,这样的数叫做合数;最小的自然数是0,最小的奇数是1,最小的质数是2,最小的合数是4.
19.买3瓶饮料和3包饼干的总价;原来有微信上有多少钱
解:3a+3b表示:买3瓶饮料和3包饼干的总价;
3(a+b)+18.90表示:原来有微信上有多少钱。
故答案为:买3瓶饮料和3包饼干的总价;原来有微信上有多少钱。
买3瓶饮料和3包饼干的总价=买饮料的瓶数×饮料的单价+买饼干的包数×饼干的单价;
原来有微信上的钱数=买3瓶饮料和3包饼干的总价+微信余额。
20.0.32;3.52
解:64÷4=16(平方分米)
16平方分米=0.16平方米
0.16×2=0.32(立方米)
16÷4=4(分米)
4分米=0.4米
(2×0.4+2×0.4+0.4×0.4)×2
=(0.8+0.8+0.16)×2
=1.76×2
=3.52(平方米)。
故答案为:0.32;3.52。
原来这根木料体积=底面积×高,其中,底面积=横截面的面积=增加的表面积÷增加面的个数; 表面积=(长×宽+长×高+宽×高)×2。
21.;
每段是这根绳子的:;每段长:米。
故答案为:;。
分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数;
每段的长度=绳子的总长÷段数,据此代入数据解答即可。
22.30
解:长宽高的和:40÷4=10(分米)
因为2、3、5都是质数,且2+3+5=10(分米),
所以长、宽、高分别是2厘米、3厘米、5厘米,
长方体的体积:2×3×5=30(立方分米)
故答案为:30。
长方体的棱长和÷4=长宽高的和;长、宽、高都是质数且和是10,据此判断长宽高是2、3、5;长方体的体积=长×宽×高。
23.1;mn
解:若m=n+1,m和n是相邻的自然数,两个相邻的自然数是互质数;
则m和n的最大公因数是1,最小公倍数mn。
故答案为:1;mn。
两个数是互质数,最大公因数是1,最小公倍数是它们的积。
24.160
解:(12+10+18)×4
=40×4
=160(厘米)
故答案为:160。
长方体棱长和=(长+宽+高)×4,根据公式计算出棱长和就是这根铁丝的长度。
25.1.25;2500
解:1250毫升=1.25升,2.5立方米=2500立方分米。
故答案为:1.25;2500。
1升=1000毫升,1立方米=1000立方分米,根据这些单位之间的进率换算单位即可。
26.
0.23=0.008 2.4-=1.8 0.8++-0.8=
2.1÷0.3=7 11.6y-9y=2.6y 1-=
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;分数加减混合运算,按照从左到右的顺序计算。
27.①3.85+1.5x=6.1
解: 1.5x=2.25
x=2.25÷1.5
x=1.5
②3x-=1.25
解:3x=2
x=2÷3
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①、②综合应用等式的性质解方程。
28.(1)解:2020年乙地空气质量达标天数是320﹣30=290(天)
(2)2017;34
(3)说法不对。因为根据甲、乙两地2017年至2022年的空气质量状况推断,2023年甲地的空气质量会好一些.因为整体甲地的空气质量较好。
解:(1)2020年乙地空气质量达标天数是320﹣30=290(天),
(2)309-275=34(天)
甲乙两地空气质量达标天数相差最多的是2017年,相差34天。
(3)说法不对。因为根据甲、乙两地2017年至2022年的空气质量状况推断,2023年甲地的空气质量会好一些.因为整体甲地的空气质量较好。
故答案为:(2)2017;34。
(1)2020年甲地空气质量达标天数-30天=2020年乙地空气质量达标天数,据此作图;
(2)2017年两点之间的格数最多,说明达标天数相差最多,他们的差就是相差的天数;
(3)答案不唯一,原因合理即可。
29.解:(4+3+2)×4÷12
=9×4÷12
=36÷12
=3(dm)
答:正方体框架的棱长是3dm。
长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12。所以先求出长方体的棱长和也就是铁丝的长度,用铁丝的长度除以12即可求出正方体的棱长。
30.解:设水星绕太阳一周是x天。
4x+13=365
4x+13-13=365-13
4x=352
4x÷4=352÷4
x=88
答:水星绕太阳一周是88天。
设水星绕太阳一周是x天,题中的等量关系是:水星绕太阳一周时间×4+13=地球绕太阳一周时间;据此列方程解答。
31.解:25×11+(25×2+11×2)×2
=25×11+(50+22)×2
=25×11+72×2
=275+144
=419(平方米)
答:铺瓷砖的面积有419平方米。
铺瓷砖的面积是去掉上面后的五个面的面积,铺瓷砖的面积=长×宽+(长×高+宽×高)×2。
32.解:8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24
答:这个班最少有24名学生。
8和12的最小公倍数就是这个班的最少人数。
33.解:96=16×6;80=16×5
96和80的最大公约数是16
这种正方形的边长最长是16厘米
(96÷16)×(80÷16)=6×5=30(块)
答:正方形的边长最长是16厘米;被剪成30块。
96和80的最大公约数是正方形最长的边长;长能剪成的块数×宽能剪成的块数=一共能剪成的块数。
34.解:设五一班有x人。
8x-20=6x+60
8x=6x+60+20
8x=6x+80
8x-6x=80
2x=80
x=40
答:五一班有40人。
买树苗需要的钱数是不变的。等量关系:五一班人数×每人出的钱数+20角=五一班人数×每人出的钱数+60角,根据等量关系列方程,根据等式性质解方程。
35.(1)解:9时4分-9时=4分
9立方分米=9000立方厘米
9000×4= 36000 (立方厘米)
50×36=1800 (平方厘米)
36000÷1800=20 ( 厘米)
答:9:04时,长方体水槽内水面高度是20厘米。
(2)解:23-20=3 (厘米)
1800×3=5400 ( 立方厘米)
5400÷9=600 (平方厘米)
答:这个长方体铁块的底面积是600平方厘米。
(1)9:04时,长方体水槽内水面高度=水流速度×水流的时间÷长方体的底面积;
(2)这个长方体铁块的底面积=上升水的体积÷铁块的高。
2024-2025学年五年级下册期末测试卷(西师大版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.杭州市2月份的气温变化莫测。小冬想知道杭州市2023年2月份的气温变化趋势,应该搜集的数据是( )
A.2023年各季度的平均气温 B.2023年各月的平均气温
C.2023年2月1日各时刻的气温 D.2023年2月份每天的平均气温
2.下列选项中,解决问题与体积有关的是( )。
A.包装一份生日礼物需要多少彩纸
B.给一个玻璃柜台各边装上角铁,需要多少角铁
C.油漆大厅里的柱子,需要多少油漆
D.一个玻璃球沉入装满水的杯子中,溢出多少水
3. 的分子加上10,要使分数的大小不变,分母应( )
A.加上24 B.乘2 C.加上10 D.除以2
4.如下图,甲、乙是用若干个同样大小的小正方体搭成的立体图形。比较甲、乙的表面积,下面说法正确的是( )。
A.S甲>S乙 B.S甲
A.m B.2m C.m或2m D.不能确定
6.下列数线上有A、B两点,不在A、B两点之间的分数是( )。
A. B. C. D.
7.下列各组数中,都是质数的是( )。
A.1、3和7 B.2、5和29 C.39、49和57 D.11、17和21
8.下图是一块长方形纸板,从四个角各切掉一个边长为5cm的正方形,然后做成一个无盖的盒子,这个盒子的占地面积是( )cm2。
A.500 B.200 C.1000 D.300
9.一杯豆浆,小红喝了杯后,觉得有点甜,兑满了热水。又喝了半杯,她一共喝了( )杯豆浆。
A. B. C. D.
10.如果将一个长方体的长、宽、高都扩大2倍,那么它的体积将扩大( )倍。
A.2 B.4 C.6 D.8
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.如一个物体的体积为8立方厘米,则这个物体有可能是一块橡皮。( )
12.真分数都比1小,假分数都比1大。( )
13.体积相等的两个长方体,表面积也相等。( )
14.兰兰同学“六一”儿童节拍了40张照片,其中有24张是她喜欢的。她不喜欢的照片占所拍照片的。( )
15.用三个数字4、0、2任意组成一个三位数,有些不一定是2和3的倍数。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个等腰三角形的两边长分别是 米和 米,这个三角形的周长是 米。
17.用27个棱长是2cm的小正方体拼成一个大正方体(如图1)。从这个拼成的大正方体上取出3个小正方体(如图2),剩下几何体的表面积比原来大正方体的表面积多 cm2。
18.最小的自然数是 ,最小的奇数是 ,最小的质数是 ,最小的合数是 .
19.小塘买了a元/瓶的饮料3瓶,b元/包的饼干3包,微信支付后,其余额显示18.90元。3a+3b表示 ;3(a+b)+18.90表示 。
20.如下图,把一根长2米且横截面是正方形的长方体木料截成3段,表面积增加了64dm2。原来这根木料体积是 m3,表面积是 m2。
21.一根绳子长5米,把它平均分成6段,每段是这根绳子的 ,每段长 米。
22.一个长方体,它的棱长总和是40dm,且长、宽、高都是质数,这个长方体的体积是 dm3。
23.两个非0自然数m、n,若m=n+1,则m和n的最大公因数是 ,最小公倍数是 。
24.张强制作一个灯笼,需要用铁丝做一个长12厘米,宽10厘米,高18厘米的长方体框架,这根铁丝的长度至少 厘米。(接头处忽略不计)
25.小明到超市买了一瓶1250毫升的饮料,相当于 升。存放饮料的展示柜体积是2.5立方米,相当于 立方分米。
阅卷人 四、计算题(20分)
得分
26.直接写出得数
0.23= 2.4-= 0.8++-0.8=
2.1÷0.3= 11.6y-9y= 1-=
27.解方程
①3.85+1.5x=6.1 ②3x-=1.25
阅卷人 五、操作题(10分)
得分
28.请根据不完整的统计图完成下面各题。
(1)2020年乙地空气质量达标天数比甲地少30天,根据这一信息把下边的统计图补充完整。
(2)甲乙两地空气质量达标天数相差最多的是 年,相差 天。
(3)有人说:2023年乙地空气质量达标天数一定会超过甲地,他说的对吗?。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.小林在自主学习时,用一根铁丝刚好围成一个长4dm、宽3dm、高2dm的长方体框架,之后他又用这根铁丝围成一个最大的正方体框架(且没有剩余)。正方体框架的棱长是多少dm
30.太阳系的行星中,水星离太阳最近,地球绕太阳一周是365天,比水星绕太阳一周时间的4倍还多13天,水星绕太阳一周是多少天?(列方程解答)
31.落实双减政策,某学校为了开设游泳课新建了一个游泳馆,长25米,宽11米,深2米。需要在游泳池的四周和底面铺上一层瓷砖,请问铺瓷砖的面积有多少平方米?
32.某小学六(2)班的学生分组进行植树活动,如果按8人一组,正好分完,如果按12人一组,也正好分完。这个班最少有多少名学生?
33.一块长方形铁皮,长96厘米,宽80厘米,要把它剪成同样大小的正方形且没有剩余,这种正方形的边长最长是多少?被剪成几块?
34.洒下绿色,播种希望,植树是我们和春天不变的约定。为了响应植树节的号召,某校五(1)班同学计划买树苗来种树,如果每人出8角,就多2元;如果每人出6角,就少6元,五(1)班有多少人?(列方程解答)
35.如下图所示,有一个无水的长方体水槽,一个水龙头从9:00开始向水槽内注水,水流速度为9dm3/分,9:04停止注水。接着在水槽内放入一个高为9厘米的长方体铁块,使其全部浸没在水中。从开始注水到铁块全部浸没在水中,水槽的水面高度变化情况如图中所示。
(1)9:04时,长方体水槽内水面高度是多少厘米?
(2)这个长方体铁块的底面积是多少平方厘米
答案解析部分
1.D
解:想知道杭州市2023年2月份的气温变化趋势,就要知道2023年2月份每天的平均气温。
故答案为:D。
先要收集出2023年2月份每天的平均气温,才能知道杭州市2023年2月份的气温变化趋势。
2.D
解:A项:求的是表面积;
B项:求的是棱长和;
C项:求的是表面积;
D项:求的是体积。
故答案为:D。
物体所占空间的大小,叫做物体的体积。所以一个玻璃球沉入装满水的杯子中,溢出多少水,其实就是求这个玻璃球的体积。
3.A
的分子加上10,5+10=15,15÷5=3,分子扩大3倍,要使分数的大小不变,分母应扩大3倍,12×3=36,增加36-12=24。
故答案为:A。
此题主要考查了分数的基本性质:分数的分子和分母同时乘或者除以相同的数(零除外),分数的大小不变,根据题意,先确定分子的变化情况,再确定分母的变化情况,据此解答。
4.B
解:甲的表面积=长方体的表面积,乙的表面积=长方体的表面积+小正方体2个面的面积;所以甲的表面积<乙的表面积。
故答案为:B。
物体表面的面积,叫做它的表面积,甲的表面积与长方体的表面积相等,乙的表面积比长方体的表面积大,所以甲的表面积<乙的表面积。
5.B
解:++
=+
=2(米)。
故答案为:B。
三角形任意两边之和大于第三边,任意两边之差小于第三边,所以这个等腰三角形的另一个条边长米,三角形的周长=三角形三条边的长度相加。
6.A
解:A项:=1÷4=0.25;
B项:=2÷3≈0.67;
C项:=5÷6≈0.83;
D项:=3÷2=1.5;
不在A、B两点之间。
故答案为:A。
分数化成小数,用分数的分子除以分母,A、B两点之间的数大约在0.5和1.6之间,则不在A、B两点之间。
7.B
A选项中“1”不是质数;B选项中都是质数;C选项中“49”不是质数;D选项中“21”不是质数。
故答案为:B
只有1和它本身两个因数的数,叫做质数;除了1和它本身以外还有其他因数的数叫做合数。据此判断即可。
8.B
解:(30-5×2)×(20-5×2)
=(30-10)×(20-10)
=20×10
=200(平方厘米)
故答案为:B。
30厘米-2个5厘米=长方体的长,20厘米-2个5厘米=长方体的宽,长方体的长×长方体的宽=这个盒子的占地面积。
9.A
解:+=,
她一共喝了杯豆浆。
故答案为:A。
第一次喝了杯;第二次兑满了热水。又喝了半杯豆浆的一半,是杯;第一次喝的杯数+第二次喝的杯数=她一共喝的杯数。
10.D
解:2×2×2=8,长方体的长、宽、高都扩大2倍,它的体积将扩大8倍。
故答案为:D。
长方体的体积=长×宽×高;三个因数扩大的倍数相乘,就是积扩大的倍数。
11.正确
解:如一个物体的体积为8立方厘米,则这个物体有可能是一块橡皮。说法正确。
故答案为:正确。
橡皮的长可能是4厘米,宽2厘米,高1厘米,符合实际情况。
12.错误
解:真分数都比1小,假分数大于或等于1。
故答案为:错误。
真分数小于1,假分数大于或等于1。
13.错误
解:举例说明:长、宽、高分别是3厘米、2厘米、1厘米的长方体;
体积是:3×2×1=6(立方厘米)
表面积是:3×2×2+3×1×2+2×1×2
=12+6+4
=22(平方厘米)
长、宽、高是1厘米、1厘米、6厘米的长方体;
体积是:1×1×6=6(立方厘米)
表面积是:1×1×2+1×6×2+1×6×2
=2+12+12
=26(平方厘米)
可见,体积相等的两个长方体,表面积不一定相等,原题说法错误。
故答案为:错误。
根据长方体的体积公式:V=abh以及长方体的表面积公式:S=a×b×2+a×h×2+b×h×2,可举例说明,当两个长方体的体积相等,它们的长、宽、高不一定相等,那么它们的表面积也不一定相等。
14.错误
解:(40-24)÷40
=16÷40
=
所以,她不喜欢的照片占所拍照片的,原题说法错误。
故答案为:错误。
根据求一个数占另一个数的几分之几是多少,用除法计算,用不喜欢的照片数量除以照片总数,结果用分数表示即可。
15.错误
解:因为4+0+2=6,6是3的倍数,所以用三个数字4、0、2任意组成一个三位数,一定是2和3的倍数;原题说法错误。
故答案为:错误。
3的倍数是各个数位上的数字之和能整除3的数;2的倍数是0、2、4、6、8结尾的整数。
16.
解:若米为腰长,+=,
因为<,所以米为腰长时不能围成三角形;
只能是米为腰长,
所以三角形的周长=++
=+
=+
=(米)。
故答案为:。
三角形的三边关系:三角形的两边之和大于第三边,三角形的两边之差小于第三边。
本题先判断出三角形的腰长,再将三边的长度相加即可得出答案。
17.16
解:(9-5)×(2×2)
=4×4
=16(平方厘米)。
故答案为:16。
剩下几何体的表面积比原来大正方体的表面积多了4个边长2cm正方形的面积。
18.0;1;2;4
最小的自然数是0,最小的奇数是1,最小的质数是2,最小的合数是4.
故答案为:0;1;2;4.
此题主要考查了自然数、奇数、质数、合数的认识,不能被2整除的数叫做奇数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,这样的数叫做合数;最小的自然数是0,最小的奇数是1,最小的质数是2,最小的合数是4.
19.买3瓶饮料和3包饼干的总价;原来有微信上有多少钱
解:3a+3b表示:买3瓶饮料和3包饼干的总价;
3(a+b)+18.90表示:原来有微信上有多少钱。
故答案为:买3瓶饮料和3包饼干的总价;原来有微信上有多少钱。
买3瓶饮料和3包饼干的总价=买饮料的瓶数×饮料的单价+买饼干的包数×饼干的单价;
原来有微信上的钱数=买3瓶饮料和3包饼干的总价+微信余额。
20.0.32;3.52
解:64÷4=16(平方分米)
16平方分米=0.16平方米
0.16×2=0.32(立方米)
16÷4=4(分米)
4分米=0.4米
(2×0.4+2×0.4+0.4×0.4)×2
=(0.8+0.8+0.16)×2
=1.76×2
=3.52(平方米)。
故答案为:0.32;3.52。
原来这根木料体积=底面积×高,其中,底面积=横截面的面积=增加的表面积÷增加面的个数; 表面积=(长×宽+长×高+宽×高)×2。
21.;
每段是这根绳子的:;每段长:米。
故答案为:;。
分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数;
每段的长度=绳子的总长÷段数,据此代入数据解答即可。
22.30
解:长宽高的和:40÷4=10(分米)
因为2、3、5都是质数,且2+3+5=10(分米),
所以长、宽、高分别是2厘米、3厘米、5厘米,
长方体的体积:2×3×5=30(立方分米)
故答案为:30。
长方体的棱长和÷4=长宽高的和;长、宽、高都是质数且和是10,据此判断长宽高是2、3、5;长方体的体积=长×宽×高。
23.1;mn
解:若m=n+1,m和n是相邻的自然数,两个相邻的自然数是互质数;
则m和n的最大公因数是1,最小公倍数mn。
故答案为:1;mn。
两个数是互质数,最大公因数是1,最小公倍数是它们的积。
24.160
解:(12+10+18)×4
=40×4
=160(厘米)
故答案为:160。
长方体棱长和=(长+宽+高)×4,根据公式计算出棱长和就是这根铁丝的长度。
25.1.25;2500
解:1250毫升=1.25升,2.5立方米=2500立方分米。
故答案为:1.25;2500。
1升=1000毫升,1立方米=1000立方分米,根据这些单位之间的进率换算单位即可。
26.
0.23=0.008 2.4-=1.8 0.8++-0.8=
2.1÷0.3=7 11.6y-9y=2.6y 1-=
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;分数加减混合运算,按照从左到右的顺序计算。
27.①3.85+1.5x=6.1
解: 1.5x=2.25
x=2.25÷1.5
x=1.5
②3x-=1.25
解:3x=2
x=2÷3
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①、②综合应用等式的性质解方程。
28.(1)解:2020年乙地空气质量达标天数是320﹣30=290(天)
(2)2017;34
(3)说法不对。因为根据甲、乙两地2017年至2022年的空气质量状况推断,2023年甲地的空气质量会好一些.因为整体甲地的空气质量较好。
解:(1)2020年乙地空气质量达标天数是320﹣30=290(天),
(2)309-275=34(天)
甲乙两地空气质量达标天数相差最多的是2017年,相差34天。
(3)说法不对。因为根据甲、乙两地2017年至2022年的空气质量状况推断,2023年甲地的空气质量会好一些.因为整体甲地的空气质量较好。
故答案为:(2)2017;34。
(1)2020年甲地空气质量达标天数-30天=2020年乙地空气质量达标天数,据此作图;
(2)2017年两点之间的格数最多,说明达标天数相差最多,他们的差就是相差的天数;
(3)答案不唯一,原因合理即可。
29.解:(4+3+2)×4÷12
=9×4÷12
=36÷12
=3(dm)
答:正方体框架的棱长是3dm。
长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12。所以先求出长方体的棱长和也就是铁丝的长度,用铁丝的长度除以12即可求出正方体的棱长。
30.解:设水星绕太阳一周是x天。
4x+13=365
4x+13-13=365-13
4x=352
4x÷4=352÷4
x=88
答:水星绕太阳一周是88天。
设水星绕太阳一周是x天,题中的等量关系是:水星绕太阳一周时间×4+13=地球绕太阳一周时间;据此列方程解答。
31.解:25×11+(25×2+11×2)×2
=25×11+(50+22)×2
=25×11+72×2
=275+144
=419(平方米)
答:铺瓷砖的面积有419平方米。
铺瓷砖的面积是去掉上面后的五个面的面积,铺瓷砖的面积=长×宽+(长×高+宽×高)×2。
32.解:8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24
答:这个班最少有24名学生。
8和12的最小公倍数就是这个班的最少人数。
33.解:96=16×6;80=16×5
96和80的最大公约数是16
这种正方形的边长最长是16厘米
(96÷16)×(80÷16)=6×5=30(块)
答:正方形的边长最长是16厘米;被剪成30块。
96和80的最大公约数是正方形最长的边长;长能剪成的块数×宽能剪成的块数=一共能剪成的块数。
34.解:设五一班有x人。
8x-20=6x+60
8x=6x+60+20
8x=6x+80
8x-6x=80
2x=80
x=40
答:五一班有40人。
买树苗需要的钱数是不变的。等量关系:五一班人数×每人出的钱数+20角=五一班人数×每人出的钱数+60角,根据等量关系列方程,根据等式性质解方程。
35.(1)解:9时4分-9时=4分
9立方分米=9000立方厘米
9000×4= 36000 (立方厘米)
50×36=1800 (平方厘米)
36000÷1800=20 ( 厘米)
答:9:04时,长方体水槽内水面高度是20厘米。
(2)解:23-20=3 (厘米)
1800×3=5400 ( 立方厘米)
5400÷9=600 (平方厘米)
答:这个长方体铁块的底面积是600平方厘米。
(1)9:04时,长方体水槽内水面高度=水流速度×水流的时间÷长方体的底面积;
(2)这个长方体铁块的底面积=上升水的体积÷铁块的高。
同课章节目录
