期末测试卷(含答案)---2024-2025学年五年级数学下册(沪教版)
文档属性
| 名称 | 期末测试卷(含答案)---2024-2025学年五年级数学下册(沪教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年五年级下册期末测试卷(沪教版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.把一个棱长为4dm的正方体切成两个长方体,它们表面积的和比原来增加了( ) dm2。
A.8 B.16 C.32 D.64
2.下面图形中,沿线折叠后不能围成正方体的是( )。
A. B.
C. D.
3.一个长9分米,宽和高都是6分米的长方体盒子中,最多能装( )个棱长为3分米的正方体木块。
A.12 B.14 C.15
4.一个长方体的所有棱长的长度之和是72厘米,相交于某一个顶点的三条棱之和是( )厘米
A.6 B.8 C.9 D.18
5.把一个棱长为24cm的正方体铁块熔铸成一个长是48cm,宽是40cm的长方体铁块,这个长方体的高是( )cm。
A.72 B.12 C.1.2 D.7.2
6.每本笔记本x元,买了8本,付出50元,找回32元,下面列的不正确的方程是( )。
A.50-8x=32 B.8x=50-32 C.8x-50=32
7.如果x=у,根据等式的性质可以得到( )。
A.x-2=у+2 B.x÷10=у×10 C.x+4.5=у+4.5
8.x=5是方程( )的解。
A.4x-2=10 B.17-2x=7 C.40-8x=36
9.正方体的棱长扩大2倍,则体积扩大( )倍。
A.2 B.4 C.6 D.8
10.小红有48元钱,小华有x元钱,小红给了小华5元钱后,两人的钱同样多。下列方程正确的是( )。
A.x+5=48 B.48-x=5 C.x+5=48-5
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.x=0不是方程。( )
12.一个长方体最多有8条相等的棱。( )
13.一个水桶的体积大于它的容积。( )
14.一个长方体的长、宽、高分别扩大到原来的2倍,则它的体积也扩大到原来的2倍。( )
15.希望小学要统计各年级男女生戴眼镜的人数情况,绘制复式折线统计图比较合适。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个长方体的底面积是18平方厘米,高是1.5厘米,体积是 立方厘米。
17.一个长方体是由3个同样大小的正方体拼成(如图),如果右边去掉一个正方体,表面积就比原来减少24平方厘米,原来长方体的表面积是 平方厘米。
18.表示两地一周天气的变化情况,应选择 统计图;表示两个班级学生数学成绩各个等级的人数,应选择 统计图:计算一组数据的平均数时,如果该组中的一个数据突然变大,其平均数也会 (“变大”、“变小”、“不变”)。
19.铁丝焊接一个长方体框架,同一顶点上的三根铁丝长分别为1.2m、0.8m和0.5m,那么一共用了 m铁丝。
20.小丽上学期语文、数学、科学三科的平均成绩是92分,她的英语应考 分。四科的平均成绩才能达到94分。
21.把一个体积是20cm3的铁球放入一个长5cm、宽4cm的盛有水的长方体容器中,水面最多会上升 cm。
22.用一根84厘米长的铁丝做一个长8厘米、宽3厘米的长方体框架,这个长方体框架的高是 厘米,体积是 立方厘米:如果用这根铁丝做一个正方体框架,它的体积是 立方厘米。
23.鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系是:b=2a-10(b表示码数,a表示厘米数)。一双鞋长23.5厘米,是 码;一双40码的鞋,长 厘米。
24.我国有悠久的金石文化,印信是金石文化的代表之一。印信的形状多为长方体、正方体或圆柱。某广场一侧建有一个正方体印信的标志物,这个印信的棱长是15dm,把这个印信的4面镀上金色,2面刻上主题花纹。镀金色的面积是 dm2。
25.优优家上个月水费是12元,电费是x元。电费是水费的8倍。用方程表示题中的数量关系为 ,解得x= 。
阅卷人 四、计算题(20分)
得分
26.直接写出得数
- = + = - = 1- + =
27.解方程
(1)4x÷5=1.6 (2)8x-3.2x=24 (3)2.2x-0.8×4=10
阅卷人 五、操作题(10分)
得分
28.李明和林晓为了参加学校-分钟投篮比赛,提前一周进行训练,每天测试的投中个数如下表(单位:个)。
1 2 3 4 5 6 7
李明 4 7 6 8 9 9 11
林晓 9 5 4 10 5 10 6
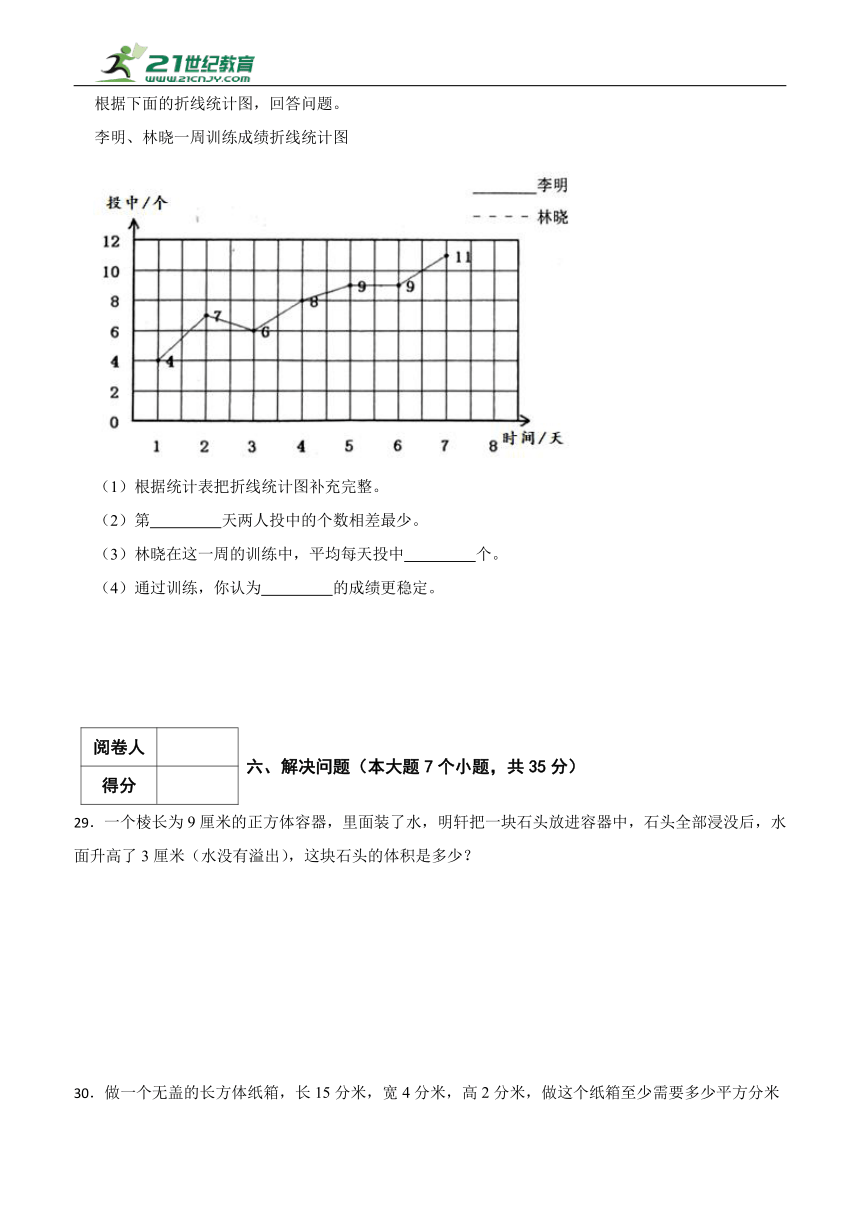
根据下面的折线统计图,回答问题。
李明、林晓一周训练成绩折线统计图
(1)根据统计表把折线统计图补充完整。
(2)第 天两人投中的个数相差最少。
(3)林晓在这一周的训练中,平均每天投中 个。
(4)通过训练,你认为 的成绩更稳定。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.一个棱长为9厘米的正方体容器,里面装了水,明轩把一块石头放进容器中,石头全部浸没后,水面升高了3厘米(水没有溢出),这块石头的体积是多少?
30.做一个无盖的长方体纸箱,长15分米,宽4分米,高2分米,做这个纸箱至少需要多少平方分米硬纸板?
31.奶奶七十大寿,妈妈送给奶奶一个长方体形状的生日蛋糕,蛋糕长3 dm,宽2 dm,高0.6dm。奶奶把它平均分成6块长方体形状的小蛋糕。奶奶是怎么分的?先画一画,再算一算每块小蛋糕有多大?
32.下面A,B,C三个图是由同样的大正方形和小正方形组成的。请你在B和C两个图中画出不同的阴影部分,使三个图形阴影部分的面积都相等并说明理由。
33.一杯果汁,明明分三次喝完。第一次喝了这杯果汁的 ,然后加满水;第二次喝了一杯的 ,然后再加满水;第三次一饮而尽。明明喝的水多还是果汁多?你是怎么想的?(提示:可以用画图、列表、列式等方式写出你的想法)
34.东东在居家学习期间,利用废旧纸板制作了一个储物盒(无盖),如图。制作这个储物盒,至少需要多大面积的纸板(纸板厚度忽略不计)?(单位:dm)
35.一间教室长12米,宽8米,高4米,黑板及门窗面积为26平方米,要粉刷四壁和顶棚(黑板、门窗和地面不刷),一共要粉刷多大面积?若每平方米用涂料0.25千克,一共需要涂料多少千克?
答案解析部分
1.C
解:4×4×2=32(dm2)
故答案为:C。
增加的表面积=正方体的边长×正方体的边长×2,据此作答即可。
2.A
解:不能围成正方体。
故答案为:A。
11种正方体的平面展开图及对立面情况:
3.A
解:9÷3=3(个),6÷3=2(个),3×2×2=12(个),所以最多能装12个棱长为2分米的正方体木块。
故答案为:A。
最多能装的个数=长方体的长里面有正方体木块棱长个数×长方体的宽里面有正方体木块棱长个数×长方体的高里面有正方体木块棱长个数,据此代入数值作答即可。
4.D
72÷4=18(厘米)
故答案为:D。
长方体的棱长总和÷4=一条长、宽、高的和,据此列式解答。
5.D
解:24×24×24÷48÷40
=13824÷48÷40
=7.2(cm)
故答案为:D。
正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,所以用正方体的体积除以熔铸成长方体的长和宽即可求出高。
6.C
解:8x是花的钱数,50元付出的钱数,花的钱数不能减付出的钱数,列的不正确的方程是8x-50=32。
故答案为:C。
付出的钱数-花的钱数=找回的钱数,花的钱数=付出的钱数-找回的钱数。
7.C
解:如果x=у,根据等式的性质可以得到x+4.5=у+4.5。
故答案为:C。
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等。
8.B
解: A:把x=5代入方程的左边,4x-2=4×5-2=18,左边≠右边,x=5不是方程的解;
B:把x=5代入方程的左边,17-2x=17-2×5=7,左边=右边,x=5是方程的解;
C:把x=5代入方程的左边,40-8x=40-8×5=0,左边≠右边,x=5不是方程的解。
故答案为:B。
使方程左右两边相等的未知数的值叫做方程的解。
9.D
解:2×2×2=8,体积扩大8倍。
故答案为:D。
正方体的棱长扩大到原来的n倍,表面积扩大到原来的n的平方倍,体积扩大到原来的n的立方倍。
10.C
解:方程正确的是:x+5=48-5。
故答案为:C。
等量关系:小华的钱数+5元=小红的钱数-5元,根据等量关系列方程即可。
11.错误
解:x=0是方程,原题说法错误。
故答案为:错误。
含有未知数的等式叫做方程。方程一定是等式,但等式不一定是方程。
12.正确
解:一个长方体最多有8条相等的棱。原题说法正确。
故答案为:正确。
特殊的长方体有两个正方形的面,围成这两个正方形面的8条棱的长度都是相等的。
13.正确
解:一个水桶的体积大于它的容积。原题说法正确。
故答案为:正确。
水桶的体积和容积的计算公式一样。体积是从外面测量的数据,容积是从里面测量的数据,所以水桶的体积一定大于容积。
14.错误
解:一个长方体的长、宽、高分别扩大到原来的2倍,则它的体积也扩大到原来的8倍。原题说法错误。
故答案为:错误。
长方体体积=长×宽×高,所以长方体体积扩大的倍数是长宽高分别扩大倍数的立方倍。
15.错误
希望小学要统计各年级男女生戴眼镜的人数情况,绘制复式条形统计图比较合适,原题说法错误。
故答案为:错误。
条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此结合题意选择合适的统计图。
16.27
解:18×1.5=27(立方厘米)。
故答案为:27。
长方体的体积=底面积×高。
17.84
解:24÷4×14
=6×14
=84(平方厘米)
故答案为:84。
原来长方体的表面积一共包括14个小正方形面的面积。去掉一个正方体后,表面积减少了4个小正方形的面,因此用表面积比原来减少的部分除以4即可求出一个正方形面的面积,用一个正方形面的面积乘14即可求出原来长方体的表面积。
18.折线;条形;变大
解:表示两地一周天气的变化情况,要表示出气温的增减变化,所以选择折线统计图;
表示两个班级学生数学成绩各个等级的人数,只需要表示出人数,应选择条形统计图;
计算一组数据的平均数时,如果该组中的一个数据突然变大,其平均数也会变大。
故答案为:折线;条形;变大。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。平均数是一组数据的平均水平,容易受极端数据的影响。
19.10
解:(1.2+0.8+0.5)×4
=2.5×4
=10(米)
故答案为:10。
长方体中相交于一个顶点的三条棱的长度,分别叫做长方体的长、宽、高;(长+宽+高)×4=长方体的棱长和。
20.100
解:94×4-92×3
=376-276
=100(分)
故答案为:100。
四科的平均成绩×4=四科的总分,三科的平均成绩×3=三科的总分,四科的总分-三科的总分=英语成绩。
21.1
20÷(5×4)
=20÷20
=1(厘米)
故答案为:1。
根据题意可知,水上升部分的体积就是铁球的体积,根据水面上升的高度=铁球的体积÷长方体的底面积,则可以计算出水面上升的高度。
22.10;240;343
解:(1)84÷4-8-3
=21-8-3
=13-3
=10(厘米)
8×3×10
=24×10
=240(立方厘米)
84÷12=7(厘米)
7×7×7
=49×7
=343(立方厘米)。
故答案为:10;240;343。
长方体框架的高=铁丝的长÷4-长-宽;长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长;其中,棱长=铁丝的长÷12。
23.37;25
解:b=2a-10
b=2×23.5-10
b=47-10
b=37(码)
b=2a-10
40=2a-10
2a=40+10
2a=50
a=50÷2
a=25(厘米)。
故答案为:37;25。
依据b=2a-10 分别代入计算即可。
24.900
解:15×15×4
=225×4
=900(平方分米)。
故答案为:900。
镀金色的面积=正方体每个面的面积×镀上金色的面的个数;其中,正方体每个面的面积=棱长×棱长。
25.电费金额÷水费金额=8;96
解:x÷12=8
x=12×8
x=96
故答案为:电费金额÷水费金额=8;96。
依据等量关系式:水费金额÷电费金额=8,列方程,解方程。
26. - = + =1 - = 1- + =
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
27.(1)4x÷5=1.6
解:4x=1.6×5
4x=8
x=8÷4
x=2
(2)8x-3.2x=24
解:4.8x=24
x=24÷4.8
x=5
(3)2.2x-0.8×4=10
解:2.2x-3.2=10
2.2x=10+3.2
2.2x=13.2
x=13.2÷2.2
x=6
综合运用等式性质解方程;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
28.(1)
(2)6
(3)7
(4)李明
解:(2)第6天两人投中的个数相差最少;
(3)(9+5+4+10+5+10+6)÷7
=49÷7
=7(个),林晓在这一周的训练中,平均每天投中7个;
(4)通过训练,你认为李明的成绩更稳定。
故答案为:(2)6;(3)7;(4)李明。
(1)依据统计表中的数据、图例,描出各点,然后连接成线,再标上数据;
(2)第6天两人投中个数的折线最接近,说明相差的最少;
(3)林晓在这一周的训练中,平均每天投中的个数=总个数÷总天数;
(4) 通过训练,我发现表示李明投篮个数的折线起伏不大,并且呈上升趋势,说明他的成绩更稳定。
29.解:9×9×3
=81×3
=243 (立方厘米)
答:这块石头的体积是243立方厘米。
这块石头的体积=正方体容器的棱长×棱长×水面上升的高度。
30.解:15×4+(15×2+4×2)×2
=60+38×2
=60+76
=136 (平方分米)
答:做这个纸箱至少需要136平方分米硬纸板。
做这个纸箱至少需要硬纸板的面积=长×宽+(长×高+宽×高)×2。
31.解:解:
3×2×0.6÷6
=6×0.6÷6
=3.6÷6
=0.6(立方分米)
答:每块小蛋糕的体积是0.6立方分米。
每块小蛋糕的体积=蛋糕的长×宽×高÷平均分的块数。
32.解:
答:三角形A、B、C是等底等高的三角形,所以面积相等。
三角形A、B、C的底=大正方形的边长+小正方形的边长;高=大正方形的边长,是等底等高的三角形,所以面积相等。
33.解:果汁:1杯
水:+=(杯)
杯<1杯
答:明明喝的果汁多。
最后全部喝完,就喝了1杯果汁;加了多少水,就喝了多少水,把加的水相加即可。
34.解:4×5+(4×1.5+5×1.5)×2
=4×5+(6+7.5)×2
=4×5+13.5×2
=20+27
=47(平方分米)
答:至少需要47平方分米的纸板。
至少需要纸板的面积=长×宽+(长×高+宽×高) ×2。
35.解:12×8+12×4×2+8×4×2-26
=96+96+64-26
=256-26
=230(平方米)
230×0.25=57.5(千克)
答:一共要粉刷230平方米。一共需要57.5千克涂料。
地面不刷,因此计算出教室另外5个面的面积之和,减去门窗及黑板的面积即可求出一共需要粉刷的面积。用需要粉刷的面积乘每平方米需要涂料的重量即可求出一共需要涂料的重量。
2024-2025学年五年级下册期末测试卷(沪教版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.把一个棱长为4dm的正方体切成两个长方体,它们表面积的和比原来增加了( ) dm2。
A.8 B.16 C.32 D.64
2.下面图形中,沿线折叠后不能围成正方体的是( )。
A. B.
C. D.
3.一个长9分米,宽和高都是6分米的长方体盒子中,最多能装( )个棱长为3分米的正方体木块。
A.12 B.14 C.15
4.一个长方体的所有棱长的长度之和是72厘米,相交于某一个顶点的三条棱之和是( )厘米
A.6 B.8 C.9 D.18
5.把一个棱长为24cm的正方体铁块熔铸成一个长是48cm,宽是40cm的长方体铁块,这个长方体的高是( )cm。
A.72 B.12 C.1.2 D.7.2
6.每本笔记本x元,买了8本,付出50元,找回32元,下面列的不正确的方程是( )。
A.50-8x=32 B.8x=50-32 C.8x-50=32
7.如果x=у,根据等式的性质可以得到( )。
A.x-2=у+2 B.x÷10=у×10 C.x+4.5=у+4.5
8.x=5是方程( )的解。
A.4x-2=10 B.17-2x=7 C.40-8x=36
9.正方体的棱长扩大2倍,则体积扩大( )倍。
A.2 B.4 C.6 D.8
10.小红有48元钱,小华有x元钱,小红给了小华5元钱后,两人的钱同样多。下列方程正确的是( )。
A.x+5=48 B.48-x=5 C.x+5=48-5
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.x=0不是方程。( )
12.一个长方体最多有8条相等的棱。( )
13.一个水桶的体积大于它的容积。( )
14.一个长方体的长、宽、高分别扩大到原来的2倍,则它的体积也扩大到原来的2倍。( )
15.希望小学要统计各年级男女生戴眼镜的人数情况,绘制复式折线统计图比较合适。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个长方体的底面积是18平方厘米,高是1.5厘米,体积是 立方厘米。
17.一个长方体是由3个同样大小的正方体拼成(如图),如果右边去掉一个正方体,表面积就比原来减少24平方厘米,原来长方体的表面积是 平方厘米。
18.表示两地一周天气的变化情况,应选择 统计图;表示两个班级学生数学成绩各个等级的人数,应选择 统计图:计算一组数据的平均数时,如果该组中的一个数据突然变大,其平均数也会 (“变大”、“变小”、“不变”)。
19.铁丝焊接一个长方体框架,同一顶点上的三根铁丝长分别为1.2m、0.8m和0.5m,那么一共用了 m铁丝。
20.小丽上学期语文、数学、科学三科的平均成绩是92分,她的英语应考 分。四科的平均成绩才能达到94分。
21.把一个体积是20cm3的铁球放入一个长5cm、宽4cm的盛有水的长方体容器中,水面最多会上升 cm。
22.用一根84厘米长的铁丝做一个长8厘米、宽3厘米的长方体框架,这个长方体框架的高是 厘米,体积是 立方厘米:如果用这根铁丝做一个正方体框架,它的体积是 立方厘米。
23.鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系是:b=2a-10(b表示码数,a表示厘米数)。一双鞋长23.5厘米,是 码;一双40码的鞋,长 厘米。
24.我国有悠久的金石文化,印信是金石文化的代表之一。印信的形状多为长方体、正方体或圆柱。某广场一侧建有一个正方体印信的标志物,这个印信的棱长是15dm,把这个印信的4面镀上金色,2面刻上主题花纹。镀金色的面积是 dm2。
25.优优家上个月水费是12元,电费是x元。电费是水费的8倍。用方程表示题中的数量关系为 ,解得x= 。
阅卷人 四、计算题(20分)
得分
26.直接写出得数
- = + = - = 1- + =
27.解方程
(1)4x÷5=1.6 (2)8x-3.2x=24 (3)2.2x-0.8×4=10
阅卷人 五、操作题(10分)
得分
28.李明和林晓为了参加学校-分钟投篮比赛,提前一周进行训练,每天测试的投中个数如下表(单位:个)。
1 2 3 4 5 6 7
李明 4 7 6 8 9 9 11
林晓 9 5 4 10 5 10 6
根据下面的折线统计图,回答问题。
李明、林晓一周训练成绩折线统计图
(1)根据统计表把折线统计图补充完整。
(2)第 天两人投中的个数相差最少。
(3)林晓在这一周的训练中,平均每天投中 个。
(4)通过训练,你认为 的成绩更稳定。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.一个棱长为9厘米的正方体容器,里面装了水,明轩把一块石头放进容器中,石头全部浸没后,水面升高了3厘米(水没有溢出),这块石头的体积是多少?
30.做一个无盖的长方体纸箱,长15分米,宽4分米,高2分米,做这个纸箱至少需要多少平方分米硬纸板?
31.奶奶七十大寿,妈妈送给奶奶一个长方体形状的生日蛋糕,蛋糕长3 dm,宽2 dm,高0.6dm。奶奶把它平均分成6块长方体形状的小蛋糕。奶奶是怎么分的?先画一画,再算一算每块小蛋糕有多大?
32.下面A,B,C三个图是由同样的大正方形和小正方形组成的。请你在B和C两个图中画出不同的阴影部分,使三个图形阴影部分的面积都相等并说明理由。
33.一杯果汁,明明分三次喝完。第一次喝了这杯果汁的 ,然后加满水;第二次喝了一杯的 ,然后再加满水;第三次一饮而尽。明明喝的水多还是果汁多?你是怎么想的?(提示:可以用画图、列表、列式等方式写出你的想法)
34.东东在居家学习期间,利用废旧纸板制作了一个储物盒(无盖),如图。制作这个储物盒,至少需要多大面积的纸板(纸板厚度忽略不计)?(单位:dm)
35.一间教室长12米,宽8米,高4米,黑板及门窗面积为26平方米,要粉刷四壁和顶棚(黑板、门窗和地面不刷),一共要粉刷多大面积?若每平方米用涂料0.25千克,一共需要涂料多少千克?
答案解析部分
1.C
解:4×4×2=32(dm2)
故答案为:C。
增加的表面积=正方体的边长×正方体的边长×2,据此作答即可。
2.A
解:不能围成正方体。
故答案为:A。
11种正方体的平面展开图及对立面情况:
3.A
解:9÷3=3(个),6÷3=2(个),3×2×2=12(个),所以最多能装12个棱长为2分米的正方体木块。
故答案为:A。
最多能装的个数=长方体的长里面有正方体木块棱长个数×长方体的宽里面有正方体木块棱长个数×长方体的高里面有正方体木块棱长个数,据此代入数值作答即可。
4.D
72÷4=18(厘米)
故答案为:D。
长方体的棱长总和÷4=一条长、宽、高的和,据此列式解答。
5.D
解:24×24×24÷48÷40
=13824÷48÷40
=7.2(cm)
故答案为:D。
正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,所以用正方体的体积除以熔铸成长方体的长和宽即可求出高。
6.C
解:8x是花的钱数,50元付出的钱数,花的钱数不能减付出的钱数,列的不正确的方程是8x-50=32。
故答案为:C。
付出的钱数-花的钱数=找回的钱数,花的钱数=付出的钱数-找回的钱数。
7.C
解:如果x=у,根据等式的性质可以得到x+4.5=у+4.5。
故答案为:C。
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等。
8.B
解: A:把x=5代入方程的左边,4x-2=4×5-2=18,左边≠右边,x=5不是方程的解;
B:把x=5代入方程的左边,17-2x=17-2×5=7,左边=右边,x=5是方程的解;
C:把x=5代入方程的左边,40-8x=40-8×5=0,左边≠右边,x=5不是方程的解。
故答案为:B。
使方程左右两边相等的未知数的值叫做方程的解。
9.D
解:2×2×2=8,体积扩大8倍。
故答案为:D。
正方体的棱长扩大到原来的n倍,表面积扩大到原来的n的平方倍,体积扩大到原来的n的立方倍。
10.C
解:方程正确的是:x+5=48-5。
故答案为:C。
等量关系:小华的钱数+5元=小红的钱数-5元,根据等量关系列方程即可。
11.错误
解:x=0是方程,原题说法错误。
故答案为:错误。
含有未知数的等式叫做方程。方程一定是等式,但等式不一定是方程。
12.正确
解:一个长方体最多有8条相等的棱。原题说法正确。
故答案为:正确。
特殊的长方体有两个正方形的面,围成这两个正方形面的8条棱的长度都是相等的。
13.正确
解:一个水桶的体积大于它的容积。原题说法正确。
故答案为:正确。
水桶的体积和容积的计算公式一样。体积是从外面测量的数据,容积是从里面测量的数据,所以水桶的体积一定大于容积。
14.错误
解:一个长方体的长、宽、高分别扩大到原来的2倍,则它的体积也扩大到原来的8倍。原题说法错误。
故答案为:错误。
长方体体积=长×宽×高,所以长方体体积扩大的倍数是长宽高分别扩大倍数的立方倍。
15.错误
希望小学要统计各年级男女生戴眼镜的人数情况,绘制复式条形统计图比较合适,原题说法错误。
故答案为:错误。
条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此结合题意选择合适的统计图。
16.27
解:18×1.5=27(立方厘米)。
故答案为:27。
长方体的体积=底面积×高。
17.84
解:24÷4×14
=6×14
=84(平方厘米)
故答案为:84。
原来长方体的表面积一共包括14个小正方形面的面积。去掉一个正方体后,表面积减少了4个小正方形的面,因此用表面积比原来减少的部分除以4即可求出一个正方形面的面积,用一个正方形面的面积乘14即可求出原来长方体的表面积。
18.折线;条形;变大
解:表示两地一周天气的变化情况,要表示出气温的增减变化,所以选择折线统计图;
表示两个班级学生数学成绩各个等级的人数,只需要表示出人数,应选择条形统计图;
计算一组数据的平均数时,如果该组中的一个数据突然变大,其平均数也会变大。
故答案为:折线;条形;变大。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。平均数是一组数据的平均水平,容易受极端数据的影响。
19.10
解:(1.2+0.8+0.5)×4
=2.5×4
=10(米)
故答案为:10。
长方体中相交于一个顶点的三条棱的长度,分别叫做长方体的长、宽、高;(长+宽+高)×4=长方体的棱长和。
20.100
解:94×4-92×3
=376-276
=100(分)
故答案为:100。
四科的平均成绩×4=四科的总分,三科的平均成绩×3=三科的总分,四科的总分-三科的总分=英语成绩。
21.1
20÷(5×4)
=20÷20
=1(厘米)
故答案为:1。
根据题意可知,水上升部分的体积就是铁球的体积,根据水面上升的高度=铁球的体积÷长方体的底面积,则可以计算出水面上升的高度。
22.10;240;343
解:(1)84÷4-8-3
=21-8-3
=13-3
=10(厘米)
8×3×10
=24×10
=240(立方厘米)
84÷12=7(厘米)
7×7×7
=49×7
=343(立方厘米)。
故答案为:10;240;343。
长方体框架的高=铁丝的长÷4-长-宽;长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长;其中,棱长=铁丝的长÷12。
23.37;25
解:b=2a-10
b=2×23.5-10
b=47-10
b=37(码)
b=2a-10
40=2a-10
2a=40+10
2a=50
a=50÷2
a=25(厘米)。
故答案为:37;25。
依据b=2a-10 分别代入计算即可。
24.900
解:15×15×4
=225×4
=900(平方分米)。
故答案为:900。
镀金色的面积=正方体每个面的面积×镀上金色的面的个数;其中,正方体每个面的面积=棱长×棱长。
25.电费金额÷水费金额=8;96
解:x÷12=8
x=12×8
x=96
故答案为:电费金额÷水费金额=8;96。
依据等量关系式:水费金额÷电费金额=8,列方程,解方程。
26. - = + =1 - = 1- + =
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
27.(1)4x÷5=1.6
解:4x=1.6×5
4x=8
x=8÷4
x=2
(2)8x-3.2x=24
解:4.8x=24
x=24÷4.8
x=5
(3)2.2x-0.8×4=10
解:2.2x-3.2=10
2.2x=10+3.2
2.2x=13.2
x=13.2÷2.2
x=6
综合运用等式性质解方程;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
28.(1)
(2)6
(3)7
(4)李明
解:(2)第6天两人投中的个数相差最少;
(3)(9+5+4+10+5+10+6)÷7
=49÷7
=7(个),林晓在这一周的训练中,平均每天投中7个;
(4)通过训练,你认为李明的成绩更稳定。
故答案为:(2)6;(3)7;(4)李明。
(1)依据统计表中的数据、图例,描出各点,然后连接成线,再标上数据;
(2)第6天两人投中个数的折线最接近,说明相差的最少;
(3)林晓在这一周的训练中,平均每天投中的个数=总个数÷总天数;
(4) 通过训练,我发现表示李明投篮个数的折线起伏不大,并且呈上升趋势,说明他的成绩更稳定。
29.解:9×9×3
=81×3
=243 (立方厘米)
答:这块石头的体积是243立方厘米。
这块石头的体积=正方体容器的棱长×棱长×水面上升的高度。
30.解:15×4+(15×2+4×2)×2
=60+38×2
=60+76
=136 (平方分米)
答:做这个纸箱至少需要136平方分米硬纸板。
做这个纸箱至少需要硬纸板的面积=长×宽+(长×高+宽×高)×2。
31.解:解:
3×2×0.6÷6
=6×0.6÷6
=3.6÷6
=0.6(立方分米)
答:每块小蛋糕的体积是0.6立方分米。
每块小蛋糕的体积=蛋糕的长×宽×高÷平均分的块数。
32.解:
答:三角形A、B、C是等底等高的三角形,所以面积相等。
三角形A、B、C的底=大正方形的边长+小正方形的边长;高=大正方形的边长,是等底等高的三角形,所以面积相等。
33.解:果汁:1杯
水:+=(杯)
杯<1杯
答:明明喝的果汁多。
最后全部喝完,就喝了1杯果汁;加了多少水,就喝了多少水,把加的水相加即可。
34.解:4×5+(4×1.5+5×1.5)×2
=4×5+(6+7.5)×2
=4×5+13.5×2
=20+27
=47(平方分米)
答:至少需要47平方分米的纸板。
至少需要纸板的面积=长×宽+(长×高+宽×高) ×2。
35.解:12×8+12×4×2+8×4×2-26
=96+96+64-26
=256-26
=230(平方米)
230×0.25=57.5(千克)
答:一共要粉刷230平方米。一共需要57.5千克涂料。
地面不刷,因此计算出教室另外5个面的面积之和,减去门窗及黑板的面积即可求出一共需要粉刷的面积。用需要粉刷的面积乘每平方米需要涂料的重量即可求出一共需要涂料的重量。
同课章节目录
