期末测试卷(含答案)---2024-2025学年六年级数学下册(北京版)
文档属性
| 名称 | 期末测试卷(含答案)---2024-2025学年六年级数学下册(北京版) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 07:38:11 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级下册期末测试卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.一个圆柱体纸筒,底面半径是1分米,高是6.28分米,这个纸筒沿高剪开,侧面展开是( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
2.在一幅比例尺是1:2000的建筑图纸上,量得学校教学楼的长是3cm,已知这座教学楼长与宽的比是3:1,则这座教学楼实际的宽是( )m。
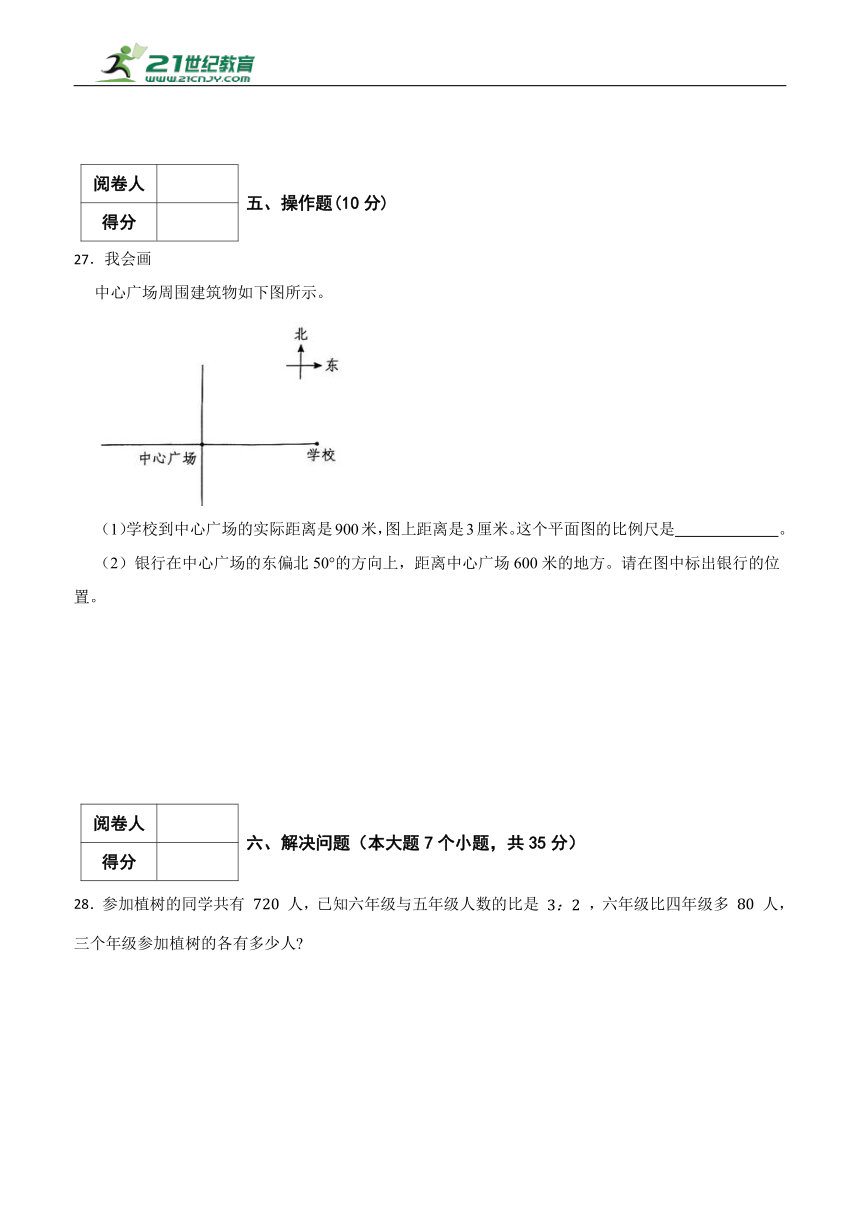
A.10 B.20 C.15
3.一段高3dm的圆柱形钢材,把它沿底面直径锯成两个半圆柱后,表面积比原来增加了 1200cm2,原来这段钢材的体积是( )cm3。
A.1884 B.3768 C.9420
4.在一幅比例尺为4:1的设计图上,量得一种精密零件的长度是2.4cm。这种精密零件的实际长度是( )。
A.6mm B.9.6cm C.6cm
5.如图,圆锥形容器内装满了水,将这些水倒入圆柱形容器( )中,正好倒满。(单位:cm)
A. B. C.
6.一根圆柱形水管,内直径是20cm,水在管中的流速是每秒40cm,每秒流过的水是( ) L。
A.62.8 B.25.12 C.12.56
7.一个底面半径为6厘米,高为10厘米的圆柱,将它的侧面沿虚线剪开,得到的平行四边形的面积是 ( )平方厘米。
A.60 B.120 C.188.4 D.376.8
8.甲圆柱形容器底面半径是乙圆柱形容器底面半径的2倍(容器直立放置),现以相同的流量同时向这两个容器注水。过了一段时间,甲、乙容器内水面的高度比是 ( )。(容器内的水都未加满)
A.1:2 B.2:1 C.4:1 D.1:4
9.一个木匠想把一个棱长为6分米的正方体木料削成一个最大的圆锥,这个圆锥形木料的体积是( )立方分米。
A.28.26 B.56.52 C.113.04 D.169.56
10.要求一个压路机滚动一周所压地面的大小,就是求圆柱的( )
A.底面积 B.侧面积 C.表面积
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.订阅《小学生数学报》的份数和钱数不成比例。( )
12.在一幅地图上,20cm的长度表示实际180km,这幅地图的比例尺是1:900000。 ( )
13.在一个比例里,两个内项互为倒数,两个外项可能是 和 。( )
14.求制作一根排水管需要多少铁皮就是求排水管的侧面积。( )
15.右面图形中有2个圆柱和1个圆锥。 ( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个圆锥体与和它等底等高的圆柱体体积相差30立方厘米,这个圆锥体的体积是 立方厘米.
17.已知=c (a、b、c均不为0),那么当a一定时,b和c成 比例;当b一定时,a和c成 比例。
18.芳芳用一块体积为288cm3的橡皮泥捏成等底等高的一个圆柱和一个圆锥,圆柱的体积是 cm3,圆锥的体积是 cm3。
19.一个圆锥形沙堆,底面半径是10m,高是6m,用这堆沙在10m宽的公路上铺2cm厚的路面,能铺 m。
20.琪琪用橡皮泥捏一个底面积6平方厘米,高3 厘米的圆锥体,浩浩也用同样多的橡皮泥捏一个同样高的圆柱,这个圆柱的底面积是 。
21.一个圆锥形零件的底面周长是25.12分米,高是6分米,这个零件的体积是 立方分米。
22.把一根4米长的圆柱木料锯成4小段圆柱,表面积增加了 60dm2.原来这跟木料的底面积是 dm2, 体积是 dm3。
23.,a与b成 比例关系。
24.压路机的滚筒呈圆柱形,轮宽2米,滚筒的直径是1米,如果滚筒每分钟转动20周,每分钟可压路面 平方米。
25. :20= =七成五= %= (填折扣) = (填小数)
阅卷人 四、计算题(20分)
得分
26.计算下面物体的表面积或体积。(单位:cm)
(1)求下面物体的表面积。
(2)求下面零件的体积。
阅卷人 五、操作题(10分)
得分
27.我会画
中心广场周围建筑物如下图所示。
(1)学校到中心广场的实际距离是900米,图上距离是3厘米。这个平面图的比例尺是 。
(2)银行在中心广场的东偏北50°的方向上,距离中心广场600米的地方。请在图中标出银行的位置。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
28.参加植树的同学共有 人,已知六年级与五年级人数的比是 ,六年级比四年级多 人,三个年级参加植树的各有多少人
29.幼儿园大班和中班共有32名男生,18名女生.已知大班男生数与女生数的比为 ,中班男生数与女生数的比为 ,那么大班有女生多少名?
30.刘爷爷向一个长和宽都是10cm、高是18cm的长方体玻璃缸中注水,当水面距离缸口2cm时,小敏在玻璃缸中放入了一个圆锥形的铅锤,铅锤完全浸没,溢出的水洒了一地。已知铅锤高15cm,底面半径为4cm。溢出多少毫升的水?
31.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不懈追求的航天梦。经过几代人的不懈奋斗,我国的航天事业取得了辉煌成就。长征五号系列(简称CZ-5)运载火箭实现数字工程化应用,大大推动了航天产品数字化的进程。整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下面是某型号运载火箭整流罩的简约示意图,整流罩本身的厚度不计,该整流罩的容积是多少?
32.老师带领学生坐车从深圳出发,前往历史悠久的甘肃开展中华文化研学活动。在一幅比例尺为1:20000000的地图上,量得深圳到甘肃的距离约是12cm。如果他们平均每时行驶96km,约行驶多少时能到达甘肃
33.一个圆柱形水槽里盛有 10 cm深的水,水槽的底面半径是10 cm,将一个高6cm的圆锥形铅锤浸入水中,水面上升了0.5cm。这个铅锤的底面积是多少?
34.长方体、正方体、圆柱的体积都可以用“底面积×高”进行计算。你能运用学过的知识,尝试计算下面这个图形的体积吗?
答案解析部分
1.B
解:3.14×1×2=6.28(分米),侧面展开是正方形。
故答案为:B。
圆柱的底面周长=π×半径×2=高,则这个纸筒沿高剪开,侧面展开是正方形。
2.B
解: 3÷=6000(厘米)
6000厘米=60米
60×=20(米)
故答案为:B。
根据“实际距离=图上距离÷比例尺”即可求出教学楼的长。由“实际长与宽的比是3:1”可知,宽是长的,根据分数乘法的意义,用长乘就是宽。
3.C
解:3分米=30厘米
1200÷2÷30
=600÷30
=20(厘米)
3.14×(20÷2)2×30
=3.14×100×30
=314×30
=9420(立方厘米)
故答案为:C。
把这个圆柱沿直径锯成两个半圆柱后,表面积比原来增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面直径,已知表面积增加了1200平方厘米,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
4.A
解:2.4÷=0.6(厘米)
0.6厘米=6毫米
故答案为:A。
依据“实际距离=图上距离÷比例尺”即可求出这个零件的实际长度。
5.C
解:圆锥的容积:3.14×(6÷2)2×6×=3.14×18;
A:容积:3.14×(2÷2)2×6=3.14×6;
B:容积:3.14×(6÷2)2×6=3.14×54;
C:容积:3.14×(6÷2)2×2=3.14×18。
故答案为:C。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×,由此计算后选择容积相同的容器即可。
6.C
解:3.14×(20÷2)2×40
=3.14×100×40
=314×40
=12560(立方厘米)
12560立方厘米=12560毫升=12.56升
故答案为:C。
根据圆柱的体积公式:V=πr2h,把数据代入公式解答即可。
7.D
解: 2×3.14×6×10
=6.28×6×10
=37.68×10
=376.8(平方厘米)
故答案为:D。
此题主要考查了圆柱的侧面积,不管侧面积是什么图形,它的面积都等于圆柱的底面周长与高的积,据此列式解答。
8.D
解:假设水的体积是V,甲圆柱的底面半径是2r,高为H,乙圆柱的底面半径为r,高为h,
H==
h=
H: h=:==1:4
故答案为:D。
此题可以看做是甲乙圆柱体积相同,甲圆柱的底面半径是乙圆柱的底面半径的2倍,求甲乙高的比;可以假设水体积是V,甲圆柱的底面半径是2r,高为H;乙圆柱的底面半径是r,高为h,由此利用圆柱的体积公式即可得出两个圆柱的高,从而求出它们的高的比。
9.B
解:6÷2=3(分米)
×3.14×32×6
=×3.14×9×6
=9.42×6
=56.52(立方分米)
故答案为:B。
此题主要考查了圆锥体积的应用,将一个棱长6分米的正方体木料削成一个最大的圆锥,这个圆锥形木料的底面直径和高均等于正方体的棱长,先求出圆锥的底面半径,然后用公式:V=πr2h,据此列式解答。
10.B
解:要求一个压路机滚动一周所压地面的大小,就是求圆柱的侧面积。
故答案为:B。
根据生活经验可知压路机压路面时压路机的前轮只是侧面与地面接触,因此要求一个压路机滚动一周所压地面的大小,就是求圆柱的侧面积。
11.错误
钱数÷份数=学习报的单价,学习报的单价是固定不变的,份数和钱数成反比例,本题错。
故答案为:错误。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量,它们的关系称为反比例关系。
12.正确
解:180千米=18000000厘米,
20:18000000=1:900000;
故答案为:正确。
比例尺是图上距离与实际距离的比,换算完单位后,再作比化简即可。
13.错误
解: × =
两个外项的乘积不是1,所以原说法错误。
故答案为:错误。
根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。利用倒数的意义可知,两个内项互为倒数,则两个外项也互为倒数,则两个外项的乘积是1。据此判断。
14.正确
解: 求制作一根排水管需要多少铁皮就是求排水管的侧面积。 说法正确。
故答案为:正确。
根据圆柱体的侧面积的定义知道,圆柱侧面积是指将一个圆柱体沿高展开后得到的长方形的面积, 因为圆柱形铁皮排水管是没有上底和下底的无底管道,则求需要的铁皮面积实际上是求其侧面积。
15.错误
解: 图形中有1个圆柱和1个圆锥。原说法错误。
故答案为:错误。
圆柱:由两个平行且全等的圆面以及连接这两个圆面的曲面(侧面)围成的几何体。圆锥:由一个圆面(底面)、一个顶点(锥顶)以及连接底面圆周与顶点的曲面(侧面)围成的几何体。据此判断。
16.15
解:30÷2=15(立方厘米),
答:这个圆锥的体积是15立方厘米.故答案为:15.
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱比圆锥的体积大了2倍,由此即可解答.
17.正;反
解:当a一定时,a=,那么b和c成正比例;当b一定时,b=ac,所以a和c成反比例。
故答案为:正;反。
当k一定时,k=(x,y≠0),那么x和y成正比例;
当k一定时,k=xy(x,y≠0),那么x和y成反比例。
18.216;72
解:圆锥的体积:288÷(3+1)
=288÷4
=72(cm3)
圆柱的体积:72×3=216(cm3)
故答案为:216;72。
等底等高的圆柱的体积是圆锥体积的3倍,然后根据和倍问题的计算公式:和÷(倍数+1)=1份数,计算出圆锥的体积,再用圆锥的体积乘3,计算出圆柱的体积。
19.3140
解:2cm=0.02m
3.14×102×6×÷(10×0.02)
=628÷0.2
=3140(m)
故答案为:3140。
这堆沙不论堆成圆锥还是长方体,形状虽然变了,但体积大小不变。根据圆锥的体积计算公式“V=πr2h”计算出这个圆锥形沙堆的体积,再根据长方体体积计算公式“V=abh”即可求出用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少m,注意单位换算。
20.2平方厘米
解:×6×3
=2×3
=6(立方厘米)
6÷3=2(平方厘米)
故答案为:2平方厘米。
此题主要考查了圆柱和圆锥体积的计算,由于两人用的橡皮泥相同,体积相等,圆锥体积公式为V=πr2h,圆柱体积为V=πr2h,先求出圆锥的体积,也是圆柱的体积,然后用圆柱的体积÷高=底面积,据此列式解答。
21.100.48
解:25.12÷2÷3.14
=12.56÷3.14
=4(分米)
3.14×42×6×
=3.14×16×6×
=50.24×6×
=301.44×
=100.48(立方分米)
故答案为:100.48。
已知圆锥的底面周长,可以求出圆锥的底面半径,C÷2÷π=r,要求圆锥的体积,应用公式:V=πr2h,据此列式解答。
22.10;400
解:4米=40分米
S=60÷(2×3)=10(dm2)
V=10×40=400(dm3)
故答案为:10,400。
将圆柱锯成4段,需要锯3次(4-1=3),每次锯断会增加2个底面,因此总共增加的底面积数量为:2×3=6(个);表面积增加的60平方分米即为新增的6个底面积之和,因此每个底面积为:60÷6=10(dm2);最后根据圆柱体积等于底面积乘以高,计算得出木料的体积即可。
23.反
解:,则ab=6×11=66,ab的乘积一定,二者成反比例关系。
故答案为:反。
把式子变为6:a=b:11,根据比例的基本性质把比例写成两个内项积等于两个外项积的形式,然后判断a、b的比值一定还是商一定,进而确定a、b成什么比例关系。
24.125.6
解:3.14×1×2=6.28(平方米)
6.28×20=125.6(平方米)
故答案为:125.6。
首项计算圆柱侧面的面积:圆柱侧面积=底面周长×高=π×直径×高。代入数据,得侧面积=3.14×1×2=6.28平方米;然后计算每分钟压路面积:因为每分钟转动20周,所以每分钟压路面积=圆柱侧面积×周数=6.28×20=125.6平方米。
25.15;4;75;七五折;0.75
解:七成五=75%=七五折=0.75
20×0.75=15
3÷0.75=4
故答案为:15,4,75,七五折,0.75。
几成几写成百分数:前边一个数表示百分之几十,后面一个数表示百分之几;
百分数化为小数:去掉百分号,将小数点向左移动两位;
比的前项=比值×比的后项;
分母=分子÷分数值。
26.(1)解:10×3.14×4
=31.4×4
=125.6(平方厘米)
(6÷2)2×3.14×2
=28.26×2
=56.52(平方厘米)
125.6+56.52=182.12(平方厘米)
(2)解:(4÷2)2×3.14×6×
=4×3.14×6×
=12.56×6×
=12.56×4
=50.24(立方厘米)
(1)图形的表面积=大圆柱的表面积+小圆柱的侧面积,侧面积=πdh,底面积=πr2;
(2)图形由圆柱挖空了等底等高的圆锥组成,所以图形的体积=圆柱的体积=Sh。
27.(1)1:30000
(2)解:600米=60000厘米
60000×=2(厘米)
解:(1)3厘米:900米=3厘米:90000厘米=(3÷3):(90000÷3)=1:30000
故答案为:(1)1:30000。
(1)已知图上距离和实际距离,要求比例尺,图上距离:实际距离=比例尺,据此解答;
(2)根据1米=100厘米,先将米化成厘米,然后用实际距离×比例尺=图上距离,据此列式计算,然后画图。
28.解:720+80=800(人)
800×=300(人)
800×=200(人)
300-80=220(人)
答:六年级参加植树的人数是300人,五年级参加植树的人数是200人,四年级参加植树的人数是220人。
六年级比四年级多80人,假设给四年级增加80人,总人数加上80,此时的总人数=参加植树的同学的总人数+80,四、五、六三个年级的人数比为3:2:3,所以六年级的人数=此时的总人数×,五年级的人数=此时的总人数×,四年级的人数=六年级的人数-80。
29.解:由于男、女生人数有比例关系,而且知道总数,所以可以用鸡免同笼的方法。假设18名女生全部是大班,则大班男生数:女生数=5:3=30:18,即男生应有30人,实际上男生有32人,相差2个人;又中班男生数:女生数=2:1=6:3,以3个中班女生换3个大班女生,每换一组可增加1个男生,所以需要换2组;所以,大班女生有18-3×2=12(名).
由于男、女生人数有比例关系,而且知道总数,所以可以用鸡免同笼的方法。假设18名女生全部是大班,将大班男生数与女生数的比化成后项是18,那么前项是30,即男生应有30人,实际上男生有32人,相差2个人,将中班男生数与女生数的比化成后项是3,那么前项是6,以3个中班女生换3个大班女生,每换一组可增加1个男生,所以需要换2组;所以,大班女生的人数=女生的总人数-3×换的组数。
30.解:
=251.2-200
=51.2(立方厘米)
51.2立方厘米=51.2毫升
答:溢出51.2mL的水。
溢出的水的体积=铅锤的体积-放入铅锤前鱼缸的空白体积,利用长方体体积公式:V=长×宽×高,以及圆锥的体积公式:V=×π×半径2×高,分别计算铅锤、鱼缸的空白体积,求其差即可。
31.解:
=125.6+25.12
=150.72(m3)=150720L
答:该整流罩的容积是150720L。
整流罩的容积=圆柱的体积+圆锥的体积,圆柱的体积=π×半径2×高,圆锥的体积=×π×半径2×高,据此代入数据计算即可。
32.解:12÷
=12×20000000
=
240000000厘米=2400千米
(时)
答:约行驶25时能到达甘肃。
已知比例尺和图上距离求实际距离,依据“实际距离=图上距离÷比例尺”即可求出实际距离,再根据路程÷速度=时间,列式解答。
33.解:10×10×3.14×0.5
=314×0.5
=157(立方厘米)
157×3÷6
=471÷6
=78.5(平方厘米)
答: 这个铅锤的底面积是78.5平方厘米。
根据排水法,水上升的体积=铅锤的体积=水槽底面积×水升高的高度,再根据S=V×3÷h求出铅锤的底面积。
34.解:6×4×3
=24×3
=72(立方分米)
6×4×(8-3)
=6×4×5
=24×5
=120(立方分米)
72+120=192(立方分米)
答:这个图形的体积是192立方分米。
观察图可知,这个图形分成了上下两个长方体,长方体的体积=长×宽×高,据此分别计算,然后相加即可。
2024-2025学年六年级下册期末测试卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.一个圆柱体纸筒,底面半径是1分米,高是6.28分米,这个纸筒沿高剪开,侧面展开是( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
2.在一幅比例尺是1:2000的建筑图纸上,量得学校教学楼的长是3cm,已知这座教学楼长与宽的比是3:1,则这座教学楼实际的宽是( )m。
A.10 B.20 C.15
3.一段高3dm的圆柱形钢材,把它沿底面直径锯成两个半圆柱后,表面积比原来增加了 1200cm2,原来这段钢材的体积是( )cm3。
A.1884 B.3768 C.9420
4.在一幅比例尺为4:1的设计图上,量得一种精密零件的长度是2.4cm。这种精密零件的实际长度是( )。
A.6mm B.9.6cm C.6cm
5.如图,圆锥形容器内装满了水,将这些水倒入圆柱形容器( )中,正好倒满。(单位:cm)
A. B. C.
6.一根圆柱形水管,内直径是20cm,水在管中的流速是每秒40cm,每秒流过的水是( ) L。
A.62.8 B.25.12 C.12.56
7.一个底面半径为6厘米,高为10厘米的圆柱,将它的侧面沿虚线剪开,得到的平行四边形的面积是 ( )平方厘米。
A.60 B.120 C.188.4 D.376.8
8.甲圆柱形容器底面半径是乙圆柱形容器底面半径的2倍(容器直立放置),现以相同的流量同时向这两个容器注水。过了一段时间,甲、乙容器内水面的高度比是 ( )。(容器内的水都未加满)
A.1:2 B.2:1 C.4:1 D.1:4
9.一个木匠想把一个棱长为6分米的正方体木料削成一个最大的圆锥,这个圆锥形木料的体积是( )立方分米。
A.28.26 B.56.52 C.113.04 D.169.56
10.要求一个压路机滚动一周所压地面的大小,就是求圆柱的( )
A.底面积 B.侧面积 C.表面积
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.订阅《小学生数学报》的份数和钱数不成比例。( )
12.在一幅地图上,20cm的长度表示实际180km,这幅地图的比例尺是1:900000。 ( )
13.在一个比例里,两个内项互为倒数,两个外项可能是 和 。( )
14.求制作一根排水管需要多少铁皮就是求排水管的侧面积。( )
15.右面图形中有2个圆柱和1个圆锥。 ( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一个圆锥体与和它等底等高的圆柱体体积相差30立方厘米,这个圆锥体的体积是 立方厘米.
17.已知=c (a、b、c均不为0),那么当a一定时,b和c成 比例;当b一定时,a和c成 比例。
18.芳芳用一块体积为288cm3的橡皮泥捏成等底等高的一个圆柱和一个圆锥,圆柱的体积是 cm3,圆锥的体积是 cm3。
19.一个圆锥形沙堆,底面半径是10m,高是6m,用这堆沙在10m宽的公路上铺2cm厚的路面,能铺 m。
20.琪琪用橡皮泥捏一个底面积6平方厘米,高3 厘米的圆锥体,浩浩也用同样多的橡皮泥捏一个同样高的圆柱,这个圆柱的底面积是 。
21.一个圆锥形零件的底面周长是25.12分米,高是6分米,这个零件的体积是 立方分米。
22.把一根4米长的圆柱木料锯成4小段圆柱,表面积增加了 60dm2.原来这跟木料的底面积是 dm2, 体积是 dm3。
23.,a与b成 比例关系。
24.压路机的滚筒呈圆柱形,轮宽2米,滚筒的直径是1米,如果滚筒每分钟转动20周,每分钟可压路面 平方米。
25. :20= =七成五= %= (填折扣) = (填小数)
阅卷人 四、计算题(20分)
得分
26.计算下面物体的表面积或体积。(单位:cm)
(1)求下面物体的表面积。
(2)求下面零件的体积。
阅卷人 五、操作题(10分)
得分
27.我会画
中心广场周围建筑物如下图所示。
(1)学校到中心广场的实际距离是900米,图上距离是3厘米。这个平面图的比例尺是 。
(2)银行在中心广场的东偏北50°的方向上,距离中心广场600米的地方。请在图中标出银行的位置。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
28.参加植树的同学共有 人,已知六年级与五年级人数的比是 ,六年级比四年级多 人,三个年级参加植树的各有多少人
29.幼儿园大班和中班共有32名男生,18名女生.已知大班男生数与女生数的比为 ,中班男生数与女生数的比为 ,那么大班有女生多少名?
30.刘爷爷向一个长和宽都是10cm、高是18cm的长方体玻璃缸中注水,当水面距离缸口2cm时,小敏在玻璃缸中放入了一个圆锥形的铅锤,铅锤完全浸没,溢出的水洒了一地。已知铅锤高15cm,底面半径为4cm。溢出多少毫升的水?
31.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不懈追求的航天梦。经过几代人的不懈奋斗,我国的航天事业取得了辉煌成就。长征五号系列(简称CZ-5)运载火箭实现数字工程化应用,大大推动了航天产品数字化的进程。整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下面是某型号运载火箭整流罩的简约示意图,整流罩本身的厚度不计,该整流罩的容积是多少?
32.老师带领学生坐车从深圳出发,前往历史悠久的甘肃开展中华文化研学活动。在一幅比例尺为1:20000000的地图上,量得深圳到甘肃的距离约是12cm。如果他们平均每时行驶96km,约行驶多少时能到达甘肃
33.一个圆柱形水槽里盛有 10 cm深的水,水槽的底面半径是10 cm,将一个高6cm的圆锥形铅锤浸入水中,水面上升了0.5cm。这个铅锤的底面积是多少?
34.长方体、正方体、圆柱的体积都可以用“底面积×高”进行计算。你能运用学过的知识,尝试计算下面这个图形的体积吗?
答案解析部分
1.B
解:3.14×1×2=6.28(分米),侧面展开是正方形。
故答案为:B。
圆柱的底面周长=π×半径×2=高,则这个纸筒沿高剪开,侧面展开是正方形。
2.B
解: 3÷=6000(厘米)
6000厘米=60米
60×=20(米)
故答案为:B。
根据“实际距离=图上距离÷比例尺”即可求出教学楼的长。由“实际长与宽的比是3:1”可知,宽是长的,根据分数乘法的意义,用长乘就是宽。
3.C
解:3分米=30厘米
1200÷2÷30
=600÷30
=20(厘米)
3.14×(20÷2)2×30
=3.14×100×30
=314×30
=9420(立方厘米)
故答案为:C。
把这个圆柱沿直径锯成两个半圆柱后,表面积比原来增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面直径,已知表面积增加了1200平方厘米,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
4.A
解:2.4÷=0.6(厘米)
0.6厘米=6毫米
故答案为:A。
依据“实际距离=图上距离÷比例尺”即可求出这个零件的实际长度。
5.C
解:圆锥的容积:3.14×(6÷2)2×6×=3.14×18;
A:容积:3.14×(2÷2)2×6=3.14×6;
B:容积:3.14×(6÷2)2×6=3.14×54;
C:容积:3.14×(6÷2)2×2=3.14×18。
故答案为:C。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×,由此计算后选择容积相同的容器即可。
6.C
解:3.14×(20÷2)2×40
=3.14×100×40
=314×40
=12560(立方厘米)
12560立方厘米=12560毫升=12.56升
故答案为:C。
根据圆柱的体积公式:V=πr2h,把数据代入公式解答即可。
7.D
解: 2×3.14×6×10
=6.28×6×10
=37.68×10
=376.8(平方厘米)
故答案为:D。
此题主要考查了圆柱的侧面积,不管侧面积是什么图形,它的面积都等于圆柱的底面周长与高的积,据此列式解答。
8.D
解:假设水的体积是V,甲圆柱的底面半径是2r,高为H,乙圆柱的底面半径为r,高为h,
H==
h=
H: h=:==1:4
故答案为:D。
此题可以看做是甲乙圆柱体积相同,甲圆柱的底面半径是乙圆柱的底面半径的2倍,求甲乙高的比;可以假设水体积是V,甲圆柱的底面半径是2r,高为H;乙圆柱的底面半径是r,高为h,由此利用圆柱的体积公式即可得出两个圆柱的高,从而求出它们的高的比。
9.B
解:6÷2=3(分米)
×3.14×32×6
=×3.14×9×6
=9.42×6
=56.52(立方分米)
故答案为:B。
此题主要考查了圆锥体积的应用,将一个棱长6分米的正方体木料削成一个最大的圆锥,这个圆锥形木料的底面直径和高均等于正方体的棱长,先求出圆锥的底面半径,然后用公式:V=πr2h,据此列式解答。
10.B
解:要求一个压路机滚动一周所压地面的大小,就是求圆柱的侧面积。
故答案为:B。
根据生活经验可知压路机压路面时压路机的前轮只是侧面与地面接触,因此要求一个压路机滚动一周所压地面的大小,就是求圆柱的侧面积。
11.错误
钱数÷份数=学习报的单价,学习报的单价是固定不变的,份数和钱数成反比例,本题错。
故答案为:错误。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量,它们的关系称为反比例关系。
12.正确
解:180千米=18000000厘米,
20:18000000=1:900000;
故答案为:正确。
比例尺是图上距离与实际距离的比,换算完单位后,再作比化简即可。
13.错误
解: × =
两个外项的乘积不是1,所以原说法错误。
故答案为:错误。
根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。利用倒数的意义可知,两个内项互为倒数,则两个外项也互为倒数,则两个外项的乘积是1。据此判断。
14.正确
解: 求制作一根排水管需要多少铁皮就是求排水管的侧面积。 说法正确。
故答案为:正确。
根据圆柱体的侧面积的定义知道,圆柱侧面积是指将一个圆柱体沿高展开后得到的长方形的面积, 因为圆柱形铁皮排水管是没有上底和下底的无底管道,则求需要的铁皮面积实际上是求其侧面积。
15.错误
解: 图形中有1个圆柱和1个圆锥。原说法错误。
故答案为:错误。
圆柱:由两个平行且全等的圆面以及连接这两个圆面的曲面(侧面)围成的几何体。圆锥:由一个圆面(底面)、一个顶点(锥顶)以及连接底面圆周与顶点的曲面(侧面)围成的几何体。据此判断。
16.15
解:30÷2=15(立方厘米),
答:这个圆锥的体积是15立方厘米.故答案为:15.
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱比圆锥的体积大了2倍,由此即可解答.
17.正;反
解:当a一定时,a=,那么b和c成正比例;当b一定时,b=ac,所以a和c成反比例。
故答案为:正;反。
当k一定时,k=(x,y≠0),那么x和y成正比例;
当k一定时,k=xy(x,y≠0),那么x和y成反比例。
18.216;72
解:圆锥的体积:288÷(3+1)
=288÷4
=72(cm3)
圆柱的体积:72×3=216(cm3)
故答案为:216;72。
等底等高的圆柱的体积是圆锥体积的3倍,然后根据和倍问题的计算公式:和÷(倍数+1)=1份数,计算出圆锥的体积,再用圆锥的体积乘3,计算出圆柱的体积。
19.3140
解:2cm=0.02m
3.14×102×6×÷(10×0.02)
=628÷0.2
=3140(m)
故答案为:3140。
这堆沙不论堆成圆锥还是长方体,形状虽然变了,但体积大小不变。根据圆锥的体积计算公式“V=πr2h”计算出这个圆锥形沙堆的体积,再根据长方体体积计算公式“V=abh”即可求出用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少m,注意单位换算。
20.2平方厘米
解:×6×3
=2×3
=6(立方厘米)
6÷3=2(平方厘米)
故答案为:2平方厘米。
此题主要考查了圆柱和圆锥体积的计算,由于两人用的橡皮泥相同,体积相等,圆锥体积公式为V=πr2h,圆柱体积为V=πr2h,先求出圆锥的体积,也是圆柱的体积,然后用圆柱的体积÷高=底面积,据此列式解答。
21.100.48
解:25.12÷2÷3.14
=12.56÷3.14
=4(分米)
3.14×42×6×
=3.14×16×6×
=50.24×6×
=301.44×
=100.48(立方分米)
故答案为:100.48。
已知圆锥的底面周长,可以求出圆锥的底面半径,C÷2÷π=r,要求圆锥的体积,应用公式:V=πr2h,据此列式解答。
22.10;400
解:4米=40分米
S=60÷(2×3)=10(dm2)
V=10×40=400(dm3)
故答案为:10,400。
将圆柱锯成4段,需要锯3次(4-1=3),每次锯断会增加2个底面,因此总共增加的底面积数量为:2×3=6(个);表面积增加的60平方分米即为新增的6个底面积之和,因此每个底面积为:60÷6=10(dm2);最后根据圆柱体积等于底面积乘以高,计算得出木料的体积即可。
23.反
解:,则ab=6×11=66,ab的乘积一定,二者成反比例关系。
故答案为:反。
把式子变为6:a=b:11,根据比例的基本性质把比例写成两个内项积等于两个外项积的形式,然后判断a、b的比值一定还是商一定,进而确定a、b成什么比例关系。
24.125.6
解:3.14×1×2=6.28(平方米)
6.28×20=125.6(平方米)
故答案为:125.6。
首项计算圆柱侧面的面积:圆柱侧面积=底面周长×高=π×直径×高。代入数据,得侧面积=3.14×1×2=6.28平方米;然后计算每分钟压路面积:因为每分钟转动20周,所以每分钟压路面积=圆柱侧面积×周数=6.28×20=125.6平方米。
25.15;4;75;七五折;0.75
解:七成五=75%=七五折=0.75
20×0.75=15
3÷0.75=4
故答案为:15,4,75,七五折,0.75。
几成几写成百分数:前边一个数表示百分之几十,后面一个数表示百分之几;
百分数化为小数:去掉百分号,将小数点向左移动两位;
比的前项=比值×比的后项;
分母=分子÷分数值。
26.(1)解:10×3.14×4
=31.4×4
=125.6(平方厘米)
(6÷2)2×3.14×2
=28.26×2
=56.52(平方厘米)
125.6+56.52=182.12(平方厘米)
(2)解:(4÷2)2×3.14×6×
=4×3.14×6×
=12.56×6×
=12.56×4
=50.24(立方厘米)
(1)图形的表面积=大圆柱的表面积+小圆柱的侧面积,侧面积=πdh,底面积=πr2;
(2)图形由圆柱挖空了等底等高的圆锥组成,所以图形的体积=圆柱的体积=Sh。
27.(1)1:30000
(2)解:600米=60000厘米
60000×=2(厘米)
解:(1)3厘米:900米=3厘米:90000厘米=(3÷3):(90000÷3)=1:30000
故答案为:(1)1:30000。
(1)已知图上距离和实际距离,要求比例尺,图上距离:实际距离=比例尺,据此解答;
(2)根据1米=100厘米,先将米化成厘米,然后用实际距离×比例尺=图上距离,据此列式计算,然后画图。
28.解:720+80=800(人)
800×=300(人)
800×=200(人)
300-80=220(人)
答:六年级参加植树的人数是300人,五年级参加植树的人数是200人,四年级参加植树的人数是220人。
六年级比四年级多80人,假设给四年级增加80人,总人数加上80,此时的总人数=参加植树的同学的总人数+80,四、五、六三个年级的人数比为3:2:3,所以六年级的人数=此时的总人数×,五年级的人数=此时的总人数×,四年级的人数=六年级的人数-80。
29.解:由于男、女生人数有比例关系,而且知道总数,所以可以用鸡免同笼的方法。假设18名女生全部是大班,则大班男生数:女生数=5:3=30:18,即男生应有30人,实际上男生有32人,相差2个人;又中班男生数:女生数=2:1=6:3,以3个中班女生换3个大班女生,每换一组可增加1个男生,所以需要换2组;所以,大班女生有18-3×2=12(名).
由于男、女生人数有比例关系,而且知道总数,所以可以用鸡免同笼的方法。假设18名女生全部是大班,将大班男生数与女生数的比化成后项是18,那么前项是30,即男生应有30人,实际上男生有32人,相差2个人,将中班男生数与女生数的比化成后项是3,那么前项是6,以3个中班女生换3个大班女生,每换一组可增加1个男生,所以需要换2组;所以,大班女生的人数=女生的总人数-3×换的组数。
30.解:
=251.2-200
=51.2(立方厘米)
51.2立方厘米=51.2毫升
答:溢出51.2mL的水。
溢出的水的体积=铅锤的体积-放入铅锤前鱼缸的空白体积,利用长方体体积公式:V=长×宽×高,以及圆锥的体积公式:V=×π×半径2×高,分别计算铅锤、鱼缸的空白体积,求其差即可。
31.解:
=125.6+25.12
=150.72(m3)=150720L
答:该整流罩的容积是150720L。
整流罩的容积=圆柱的体积+圆锥的体积,圆柱的体积=π×半径2×高,圆锥的体积=×π×半径2×高,据此代入数据计算即可。
32.解:12÷
=12×20000000
=
240000000厘米=2400千米
(时)
答:约行驶25时能到达甘肃。
已知比例尺和图上距离求实际距离,依据“实际距离=图上距离÷比例尺”即可求出实际距离,再根据路程÷速度=时间,列式解答。
33.解:10×10×3.14×0.5
=314×0.5
=157(立方厘米)
157×3÷6
=471÷6
=78.5(平方厘米)
答: 这个铅锤的底面积是78.5平方厘米。
根据排水法,水上升的体积=铅锤的体积=水槽底面积×水升高的高度,再根据S=V×3÷h求出铅锤的底面积。
34.解:6×4×3
=24×3
=72(立方分米)
6×4×(8-3)
=6×4×5
=24×5
=120(立方分米)
72+120=192(立方分米)
答:这个图形的体积是192立方分米。
观察图可知,这个图形分成了上下两个长方体,长方体的体积=长×宽×高,据此分别计算,然后相加即可。
同课章节目录
