期末测试卷(含答案)---2024-2025学年六年级数学下册(西师大版)
文档属性
| 名称 | 期末测试卷(含答案)---2024-2025学年六年级数学下册(西师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 656.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 07:39:00 | ||
图片预览



文档简介
保密★启用前
2024-2025学年六年级下册期末测试卷(西师大版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.下列说法正确的是( )。
A.正方体有6顶点 B.长方体有12条棱 C.正方体比长方体大
2. 3加上%后,比原来的数( )。
A.> B.< C.=
3.能与 : 组成比例的是( )。
A.5:4 B.4:5 C. : D. :
4.面动成体。如图,长方形的长为6cm,宽为5cm。按照图中的方式快速旋转可以得到( )。
A.一个底面直径是6cm、高为5cm的圆柱
B.一个底面半径是6cm、高为5cm的圆柱
C.一个底面周长是6cm、高为5cm的圆柱
D.一个底面直径是6cm、高为5cm的圆锥
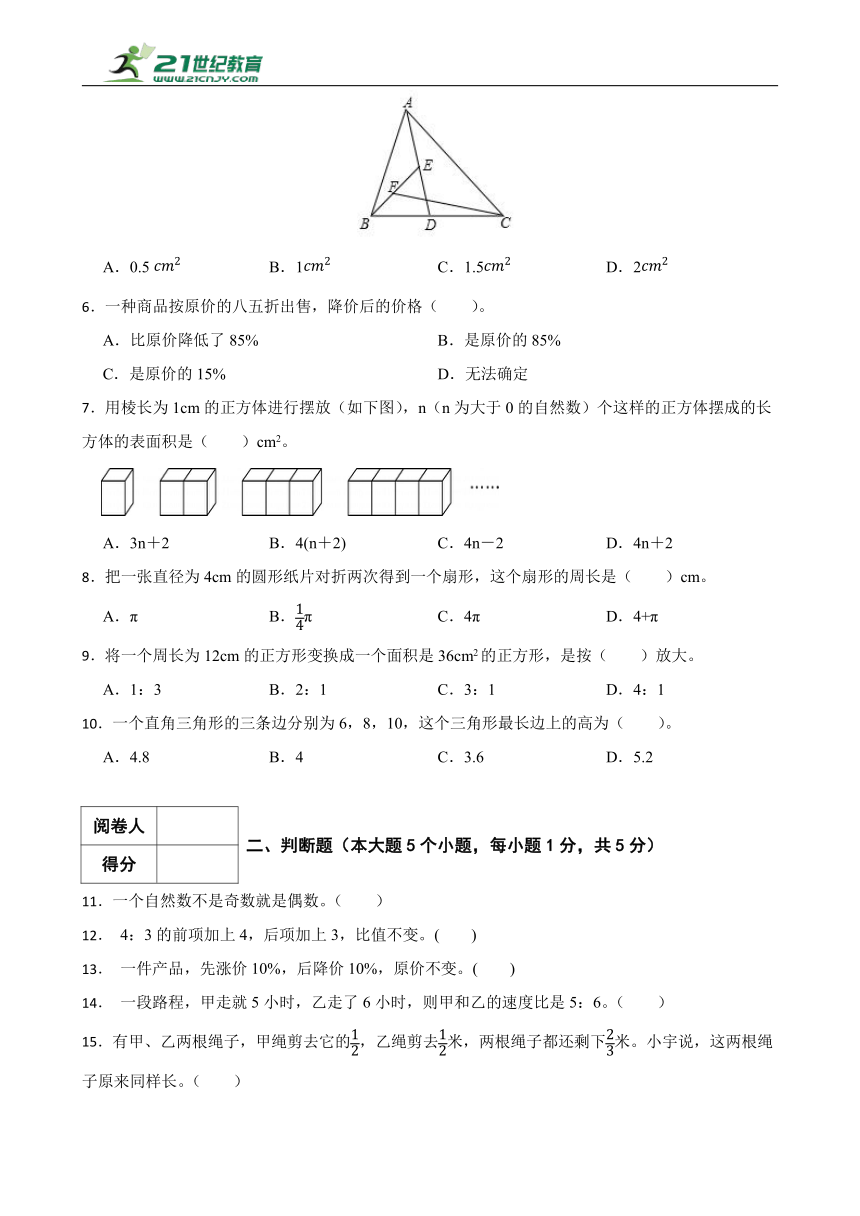
5.如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8,则△BCF的面积为( )
A.0.5 B.1 C.1.5 D.2
6.一种商品按原价的八五折出售,降价后的价格( )。
A.比原价降低了85% B.是原价的85%
C.是原价的15% D.无法确定
7.用棱长为1cm的正方体进行摆放(如下图),n(n为大于0的自然数)个这样的正方体摆成的长方体的表面积是( )cm2。
A.3n+2 B.4(n+2) C.4n-2 D.4n+2
8.把一张直径为4cm的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )cm。
A.π B.π C.4π D.4+π
9.将一个周长为12cm的正方形变换成一个面积是36cm2的正方形,是按( )放大。
A.1:3 B.2:1 C.3:1 D.4:1
10.一个直角三角形的三条边分别为6,8,10,这个三角形最长边上的高为( )。
A.4.8 B.4 C.3.6 D.5.2
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.一个自然数不是奇数就是偶数。( )
12. 4:3的前项加上4,后项加上3,比值不变。( )
13. 一件产品,先涨价10%,后降价10%,原价不变。( )
14. 一段路程,甲走就5小时,乙走了6小时,则甲和乙的速度比是5:6。( )
15.有甲、乙两根绳子,甲绳剪去它的,乙绳剪去米,两根绳子都还剩下米。小宇说,这两根绳子原来同样长。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.甲数和乙数的比是5:6,乙数和丙数的比是3:2,则甲数和丙数的比是 。
17. 6g的盐加入10g水中,盐占盐水的 %。
18. 5kg的大米平均分给6个人,每份占 ;每人得 kg。
19. 3.14;3.01;30%从大到小的顺序是 > > 。
20.若a:b=4:5,其中a=20,则b= 。
21. ,( A、B都不为0),那么A与B的比值是 。
22.底面积85cm2、高是12cm的圆锥的体积是 与它等底等高的圆柱体积是 。
23.5km是8km的 %;8km比5km长 %;比50kg轻20%的是 kg;35m比 m长40%。
24.下图是由大、小两个正方形组成的,大正方形的边长是6厘米,小正方形的边长是4厘米,图中阴影部分的面积是 平方厘米。
25.一个装有水的长方体容器长13cm,宽10cm,把一个圆柱和一个圆锥都放入容器中,水面上升了2cm。已知圆柱和圆锥等底等高,圆锥完全浸入水中,圆柱有的高露出水面,则圆柱的体积是 cm3。
阅卷人 四、计算题(20分)
得分
26.直接写出得数。
16.5÷10%= 1-+= 1.05×= ×÷×=
1-0.62= -×= 1.5a-a= 0.9×9.9+0.09=
27.解方程。
①x+36=100 ②0.3x+3.2×5=22 ③0.35:=x:6
阅卷人 五、操作题(10分)
得分
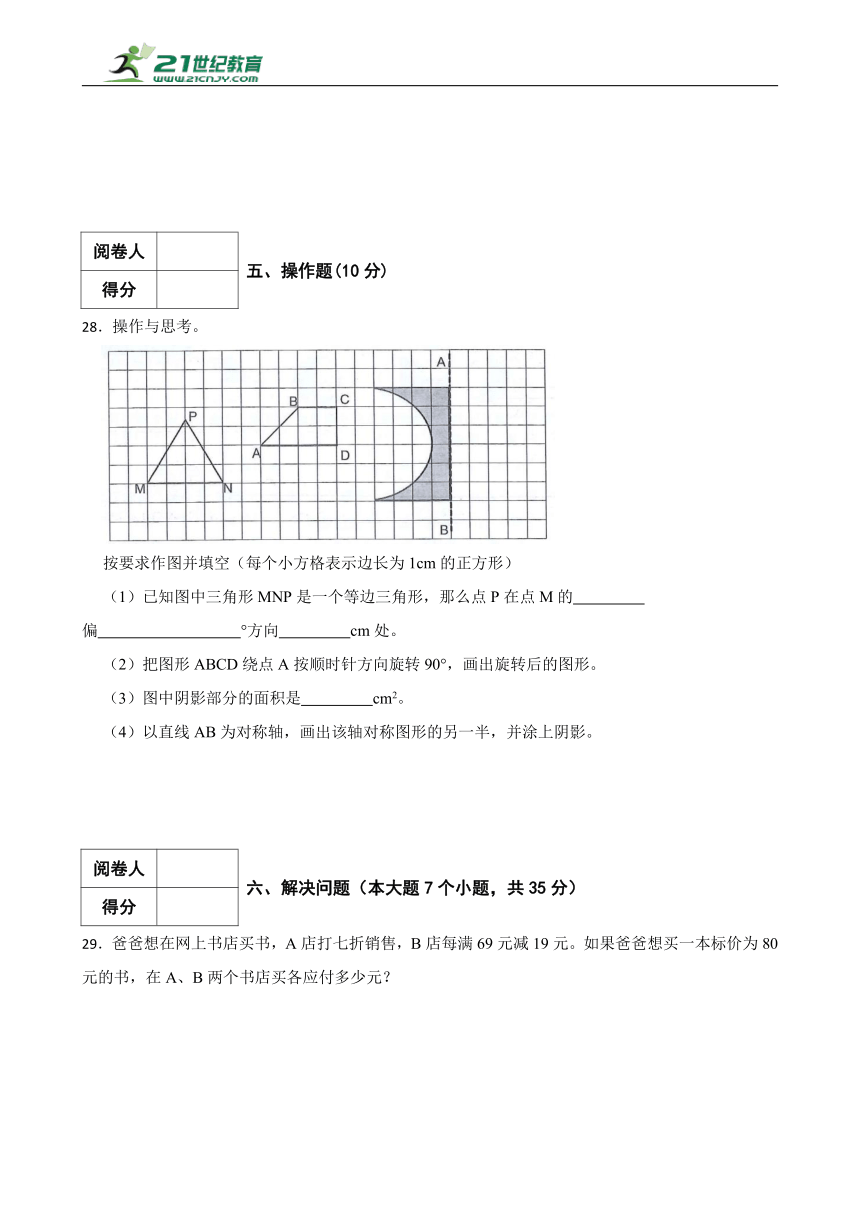
28.操作与思考。
按要求作图并填空(每个小方格表示边长为1cm的正方形)
(1)已知图中三角形MNP是一个等边三角形,那么点P在点M的 偏 °方向 cm处。
(2)把图形ABCD绕点A按顺时针方向旋转90°,画出旋转后的图形。
(3)图中阴影部分的面积是 cm2。
(4)以直线AB为对称轴,画出该轴对称图形的另一半,并涂上阴影。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.爸爸想在网上书店买书,A店打七折销售,B店每满69元减19元。如果爸爸想买一本标价为80元的书,在A、B两个书店买各应付多少元?
30.陈老师把10000元人民币存入银行,整存整取五年,他准备到期后将获得的利息用来资助贫困学生。如果按年利率3.87%计算,到期后陈老师可以拿出多少钱来资助贫困生?
31. 一个篮球比一个足球便宜50元,买了4个篮球和5个足球花了520元,则一个篮球和一个足球分别多少元
32.如图所示,平行四边形ABCD的周长是45cm,以BC为底的高是7cm,以CD为底的高是8cm,求平行四边形ABCD的面积。(用方程解答)
33.一辆大客车从温岭开往某地,出发时车上还有5个空座位,中途第一次停站时,车上有的乘客下车,又有15人上车,这时车上座位正好坐满。这辆大客车一共有多少个乘客座位?(先将线段图补充完整,再列式计算)
34.一项工程,甲队单独修需要20天,乙队单独修需要30天。两队先合修8天后,剩下的工程由乙队单独去修,还需要几天完成?
35.如图所示,圆柱形容器甲是空的,正方形容器乙中水深6.28厘米,将容器乙中的水全部倒入容器甲中,这时水深多少厘米?
答案解析部分
1.B
解:A项:正方体有8顶点,原题干说法错误;
B项:长方体有12条棱,原题干说法正确;
C项:正方体和长方体没有具体的数据,无法比较大小,原题干说法错误。
故答案为:B。
长方体、正方体都有8个顶点,12条棱,6个面;正方体和长方体没有具体的数据,无法比较大小。
2.B
解:3÷3%=3÷0.03=100,所以3%<3。
故答案为:B。
一个非0的数加上%后,缩小了100倍。
3.B
:=,A选项5:4=,B选项4:5=,C选项:=,D选项:=。
故答案为:B.
比值相等的两个比能组成比例,据此解答即可。
4.A
解:可以得到一个底面直径是6cm、高为5cm的圆柱。
故答案为:A。
因为旋转轴在中间,所以长方形的长就是圆柱的底面直径,长方形的宽就是圆柱的高。
5.D
解:
如图所示,从A点做BC的垂线AA',交BC于A';从E点做BC的垂线EE',交BC于E';从F点做BC的垂线FF',交BC于F'。∵AA'⊥BC,FF'⊥BC,EE'⊥BC,∴AA'∥FF'∥EE'。在△AA'D和△EE'D中,∠D=∠D,∠AA'D=∠EE'D=90°,∠A'AD=∠E'ED,∴△AA'D∽△EE'D,而E 点是AD中点,∴,AA'=2EE'。同理可证△BFF'∽△BEE',,EE'=2FF',AA'=4FF'。△ABC的面积为8 ,所以BC×AA'÷2=8,即BC×4FF'÷2=8,则BC×FF'÷2=2=S△BCF。
故答案为:D。
本题因为有条件“ 点D、E、F分别是BC、AD、BE上的中点 ”,可以构造出三角形来证明相似,这样对应三角形高的比也就是相似比,从而有大三角形△ABC的面积计算出小三角形△BCF的面积,所以分别从A点、E点、F点做三条垂线垂直于BC,再分别从△AA'D和△EE'D、△BFF'∽△BEE'这两组三角形证明相似,这样对应高的比也就可以计算出来,最后计算出△BCF的面积。
6.B
一种商品按原价的八五折出售,降价后的价格是原价的85%。
故答案为:B。
打几折,即按原价的十分之几、百分之几十出售,打八五折即按原价的出售,化成百分数即可(分数分子上的数后面加%即可)。
7.D
解:4×n+1×1×2=(4n+2)(平方厘米)。
故答案为:D。
正方体一个面的面积=棱长×棱长=1×1=1平方厘米;n(n为大于0的自然数)个这样的正方体摆成的长方体的表面积=(4n+2)。
8.D
解:4+4×π÷4=4+π。
故答案为:D。
将一个圆形纸片对折两次得到的扇形占整个圆的,这个扇形的周长=圆的直径+圆的周长÷4;其中,圆的周长=π×直径。
9.B
解:12÷4=3(厘米)
3×3=9(平方厘米)
36÷9=4
4=2×2,按照2:1放大的。
故答案为:B。
正方形的面积=边长×边长,先计算原来正方形的面积,现在正方形的面积是原来正方形面积的4倍,4=2×2,按照2:1放大的。
10.A
解:6×8÷2×2÷10
=48÷10
=4.8。
故答案为:A。
直角三角形较短的两条边直角边分别是它的底和高,这个三角形最长边上的高=直角三角形两条直角边的积÷2×2÷最长边的长度。
11.正确
解:一个自然数不是奇数就是偶数,原题说法正确.
故答案为:正确
奇数是末尾数字是1、3、5、7、9的数,偶数是末尾数字是0、2、4、6、8的数;注意0是偶数.由此判断即可.
12.正确
解:(4+4):(3+3)=8÷6=,比值不变,原题干说法正确。
故答案为:正确。
4:3的前项加上4,后项加上3,实际是比的前项和后项同时乘2,则比值不变。
13.错误
解:1×(1+10%)×(1-10%)
=1.1×0.9
=99%
99%<1,现价比原价低。
故答案为:错误。
把这件产品的原价看作单位“1”,现价=原价×(1+涨价的百分率)×(1-降价的百分率),然后比较大小。
14.错误
解:甲和乙的速度比是6:5,原题干说法错误。
故答案为:错误。
甲和乙的速度比=所用时间的反比。
15.错误
解:甲绳子的原长:米+米=米
乙绳子的原长:米+米=米
米≠米,这两根绳子原来不一样长
故答案为:错误。
甲绳剩下的长度+剩下的长度=甲绳原来的长度;乙绳剩下的长度+米=乙绳原来的长度;据此解答。
16.5:4
解:乙数:丙数=3:2=(3×2):(2×2)=6:4
所以甲数:乙数:丙数=5:6:4
甲数和丙数的比是5:4;
故答案为:5:4。
要想求甲数和丙数的比,需要将这两个比化成连比,两个比中都有乙数,对应的份数分别是6和3,而6和3的最小公倍数是6,因此,可以根据比的基本性质将乙数和丙数的比的前、后项同时乘2,即可写成连比,从而得到甲数和丙数的比。
17.37.5
解:6÷(6+10)
=6÷16
=37.5%。
故答案为:37.5。
盐占盐水的分率=盐的质量÷(盐的质量+水的质量) 。
18.;
解:1÷6=
5÷6=(千克)。
故答案为:;。
每人占的分率=1÷平均分的人数;每人分的质量=大米的总质量÷平均分的人数。
19.3.14;3.01;30%
解:30%=0.3,所以3.14>3.01>30%。
故答案为:3.14;3.01;30%。
百分数化成小数,把百分号去掉,小数点向左移动两位;然后比较大小。
20.25
解:a:b=4:5
20:b=4:5
4b=100
b=100÷4
b=25。
故答案为:25。
把a=20,代入比例中,应用比例的基本性质解比例。
21.2
解:由比例的基本性质可知A:B=1.2:=2。
故答案为:2。
比例的基本性质:两个外项的积等于两个内项的积。
22.340立方厘米;1020立方厘米
解:85×12×=340(立方厘米),所以圆锥的体积是340立方厘米;340×3=1020(立方厘米),所以与它等底等高的圆柱体积是1020立方厘米。
故答案为:340立方厘米;1020立方厘米。
圆锥的体积=底面积×高×;
等底等高圆柱的体积是圆锥体积的3倍。
23.62.5;60;40;25
解:5÷8×100%=62.5%
(8-5)÷5×100%
=3÷5×100%
=60%
50×(1-20%)
=50×80%
=40(kg)
35÷(1+40%)
=35÷140%
=25(m)
故答案为:62.5;60;40;25。
求一个数是另一个数的百分之几,这个数÷另一个数×100%;
求一个数比另一个数多(少)百分之几,大数-小数=多的(少的),(大数-小数)÷单位“1”×100%=多(少)百分之几;
已知一个数比另一个数多(少)百分之几:1+多百分之几=比较量占单位“1”的百分之几,单位“1”的量×(1+多百分之几)=比较量,1-少百分之几=比较量占单位“1”的百分之几,单位“1”的量×(1-少百分之几)=比较量。
24.36.4
解:如图所示,因为两个图形都是正方形,因此∠D=∠OCF=90°,且AD∥CF,所以∠DAO=∠OFC,而∠AOD=∠FOC,因此△ADO∽△FCO,所以。
设CO=x厘米,则OG=(4-x)厘米,DG=6-4=2厘米,因此,变形为6x=4(2+4-x),即6x=24-4x,解得x=2.4,OD=6-2.4=3.6厘米。S△ADO=6×3.6÷2=10.8(平方厘米),S△FCO=4×2.4÷2=4.8(平方厘米),S阴影面积=6×6+4×4-10.8-4.8=36.4(平方厘米)。
故答案为:36.4。
本题求阴影部分面积,观察图形可以看到阴影部分是两个梯形,而空白区域是两个三角形,很明显这两个三角形相似,此时需要证明出这两个三角形相似即可。三角形相似,则有,这时可以设CO=x厘米,比例形式就转换为未知数方程求解,自然可以解出CO和OD的值,这样三角形的底和高都有,根据三角形面积计算公式“底乘以高除以二”,两个面积也能求出,然后用两个正方形面积之和减去这两个三角形面积,就是阴影部分面积。
25.240
解:设圆柱的体积是x立方厘米。
(1-)x+x=13×10×2
x=260
x=260÷
x=240。
故答案为:240。
等底等高的圆锥的体积是圆柱体积的,依据等量关系式:(1-圆柱露出的高度)×圆柱的体积+×圆柱的体积=长方体的长×宽×上升水的高度,列方程,解方程。
26.
16.5÷10%=165 1-+= 1.05×=0.6 ×÷×=
1-0.62=0.64 -×= 1.5a-a=0.5a 0.9×9.9+0.09=9
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.①x+36=100
解: x=100-36
x=64
②0.3x+3.2×5=22
解:0.3x+16=22
0.3x=6
x=6÷0.3
x=20
③0.35:=x:6
解: x=0.35×6
x=2.1
x=2.1÷
x=3.5
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①应用等式的性质1解方程;
②综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积;
③应用比例的基本性质解比例。
28.(1)东;北;60;4
(2)解:
(3)9.87
(4)解:
解:(1)1×4=4(厘米),点P在点M的东偏北60°方向4厘米处;
(3)6×4-3.14×32÷2
=24-14.13
=9.87(平方厘米)。
故答案为:(1)东;北;60;4;(3)9.87。
(1)等边三角形每个内角是60°,三条边都相等,边长=1×格数=4厘米;在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)图中阴影部分的面积=长方形的长×宽-π×半径2÷2;
(4)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
29.解:A店:80×0.7=56(元)
B店:80-19=61(元)
答:在A书店买应付56元,在B书店买应付61元。
A店应付钱数=原价×折扣,B店应付钱数=原价-减少的钱数,据此解答。
30.解:10000×3.87%×5= 1935 (元)
答:到期后陈老师可以拿出1935元来资助贫困生。
利息=本金×利率×存期。
31.解:(520+4×50)÷(4+5)
=720÷9
=80(元)
80-50=30(元)
答:一个篮球30元,一个足球80元。
把4个篮球看作4个足球,则总钱数=原来买4个篮球和5个足球的总钱数+4×每个篮球比每个足球便宜的钱数,则足球的单价=把4个篮球看作4个足球的总钱数÷(4+5)=80元,篮球的单价=足球的单价-50元。
32.解:45÷2=(cm)
设BC的长为xcm,则CD的长为(-x)cm。
7x=(-x)×8
15x=180
x=180÷15
x=12
12×7=84(cm2)
答:平行四边形的面积为84cm2。
平行四边形的面积=底×高;依据面积相等列方程,求出底、高的长度。
33.解:
设原来乘客的人数为x人,
5+x=15
x=10
x=10÷
x=50
5+50=55(个)
答:这辆大客车一共有55个乘客座位。
依据等量关系式:出发时车上还有空座位的个数+×这辆大客车一共有乘客座位的个数=又上车的人数,列方程,解方程。
34.解:()×8
=
=
1-=
÷=10(天)
答:还需要10天完成。
乙队单独修还需要的天数=(1-甲、乙工作效率的和×合修的时间)÷乙的工作效率。
35.解:10×10×6.28=628(立方厘米)
628÷(10÷2)2÷3.14
=200÷25
=8(厘米)
答:此时水深8厘米。
水的体积=底面积×水的高度;水在圆柱中的深度=水的体积÷圆柱底面积。
2024-2025学年六年级下册期末测试卷(西师大版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.下列说法正确的是( )。
A.正方体有6顶点 B.长方体有12条棱 C.正方体比长方体大
2. 3加上%后,比原来的数( )。
A.> B.< C.=
3.能与 : 组成比例的是( )。
A.5:4 B.4:5 C. : D. :
4.面动成体。如图,长方形的长为6cm,宽为5cm。按照图中的方式快速旋转可以得到( )。
A.一个底面直径是6cm、高为5cm的圆柱
B.一个底面半径是6cm、高为5cm的圆柱
C.一个底面周长是6cm、高为5cm的圆柱
D.一个底面直径是6cm、高为5cm的圆锥
5.如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8,则△BCF的面积为( )
A.0.5 B.1 C.1.5 D.2
6.一种商品按原价的八五折出售,降价后的价格( )。
A.比原价降低了85% B.是原价的85%
C.是原价的15% D.无法确定
7.用棱长为1cm的正方体进行摆放(如下图),n(n为大于0的自然数)个这样的正方体摆成的长方体的表面积是( )cm2。
A.3n+2 B.4(n+2) C.4n-2 D.4n+2
8.把一张直径为4cm的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )cm。
A.π B.π C.4π D.4+π
9.将一个周长为12cm的正方形变换成一个面积是36cm2的正方形,是按( )放大。
A.1:3 B.2:1 C.3:1 D.4:1
10.一个直角三角形的三条边分别为6,8,10,这个三角形最长边上的高为( )。
A.4.8 B.4 C.3.6 D.5.2
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.一个自然数不是奇数就是偶数。( )
12. 4:3的前项加上4,后项加上3,比值不变。( )
13. 一件产品,先涨价10%,后降价10%,原价不变。( )
14. 一段路程,甲走就5小时,乙走了6小时,则甲和乙的速度比是5:6。( )
15.有甲、乙两根绳子,甲绳剪去它的,乙绳剪去米,两根绳子都还剩下米。小宇说,这两根绳子原来同样长。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.甲数和乙数的比是5:6,乙数和丙数的比是3:2,则甲数和丙数的比是 。
17. 6g的盐加入10g水中,盐占盐水的 %。
18. 5kg的大米平均分给6个人,每份占 ;每人得 kg。
19. 3.14;3.01;30%从大到小的顺序是 > > 。
20.若a:b=4:5,其中a=20,则b= 。
21. ,( A、B都不为0),那么A与B的比值是 。
22.底面积85cm2、高是12cm的圆锥的体积是 与它等底等高的圆柱体积是 。
23.5km是8km的 %;8km比5km长 %;比50kg轻20%的是 kg;35m比 m长40%。
24.下图是由大、小两个正方形组成的,大正方形的边长是6厘米,小正方形的边长是4厘米,图中阴影部分的面积是 平方厘米。
25.一个装有水的长方体容器长13cm,宽10cm,把一个圆柱和一个圆锥都放入容器中,水面上升了2cm。已知圆柱和圆锥等底等高,圆锥完全浸入水中,圆柱有的高露出水面,则圆柱的体积是 cm3。
阅卷人 四、计算题(20分)
得分
26.直接写出得数。
16.5÷10%= 1-+= 1.05×= ×÷×=
1-0.62= -×= 1.5a-a= 0.9×9.9+0.09=
27.解方程。
①x+36=100 ②0.3x+3.2×5=22 ③0.35:=x:6
阅卷人 五、操作题(10分)
得分
28.操作与思考。
按要求作图并填空(每个小方格表示边长为1cm的正方形)
(1)已知图中三角形MNP是一个等边三角形,那么点P在点M的 偏 °方向 cm处。
(2)把图形ABCD绕点A按顺时针方向旋转90°,画出旋转后的图形。
(3)图中阴影部分的面积是 cm2。
(4)以直线AB为对称轴,画出该轴对称图形的另一半,并涂上阴影。
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.爸爸想在网上书店买书,A店打七折销售,B店每满69元减19元。如果爸爸想买一本标价为80元的书,在A、B两个书店买各应付多少元?
30.陈老师把10000元人民币存入银行,整存整取五年,他准备到期后将获得的利息用来资助贫困学生。如果按年利率3.87%计算,到期后陈老师可以拿出多少钱来资助贫困生?
31. 一个篮球比一个足球便宜50元,买了4个篮球和5个足球花了520元,则一个篮球和一个足球分别多少元
32.如图所示,平行四边形ABCD的周长是45cm,以BC为底的高是7cm,以CD为底的高是8cm,求平行四边形ABCD的面积。(用方程解答)
33.一辆大客车从温岭开往某地,出发时车上还有5个空座位,中途第一次停站时,车上有的乘客下车,又有15人上车,这时车上座位正好坐满。这辆大客车一共有多少个乘客座位?(先将线段图补充完整,再列式计算)
34.一项工程,甲队单独修需要20天,乙队单独修需要30天。两队先合修8天后,剩下的工程由乙队单独去修,还需要几天完成?
35.如图所示,圆柱形容器甲是空的,正方形容器乙中水深6.28厘米,将容器乙中的水全部倒入容器甲中,这时水深多少厘米?
答案解析部分
1.B
解:A项:正方体有8顶点,原题干说法错误;
B项:长方体有12条棱,原题干说法正确;
C项:正方体和长方体没有具体的数据,无法比较大小,原题干说法错误。
故答案为:B。
长方体、正方体都有8个顶点,12条棱,6个面;正方体和长方体没有具体的数据,无法比较大小。
2.B
解:3÷3%=3÷0.03=100,所以3%<3。
故答案为:B。
一个非0的数加上%后,缩小了100倍。
3.B
:=,A选项5:4=,B选项4:5=,C选项:=,D选项:=。
故答案为:B.
比值相等的两个比能组成比例,据此解答即可。
4.A
解:可以得到一个底面直径是6cm、高为5cm的圆柱。
故答案为:A。
因为旋转轴在中间,所以长方形的长就是圆柱的底面直径,长方形的宽就是圆柱的高。
5.D
解:
如图所示,从A点做BC的垂线AA',交BC于A';从E点做BC的垂线EE',交BC于E';从F点做BC的垂线FF',交BC于F'。∵AA'⊥BC,FF'⊥BC,EE'⊥BC,∴AA'∥FF'∥EE'。在△AA'D和△EE'D中,∠D=∠D,∠AA'D=∠EE'D=90°,∠A'AD=∠E'ED,∴△AA'D∽△EE'D,而E 点是AD中点,∴,AA'=2EE'。同理可证△BFF'∽△BEE',,EE'=2FF',AA'=4FF'。△ABC的面积为8 ,所以BC×AA'÷2=8,即BC×4FF'÷2=8,则BC×FF'÷2=2=S△BCF。
故答案为:D。
本题因为有条件“ 点D、E、F分别是BC、AD、BE上的中点 ”,可以构造出三角形来证明相似,这样对应三角形高的比也就是相似比,从而有大三角形△ABC的面积计算出小三角形△BCF的面积,所以分别从A点、E点、F点做三条垂线垂直于BC,再分别从△AA'D和△EE'D、△BFF'∽△BEE'这两组三角形证明相似,这样对应高的比也就可以计算出来,最后计算出△BCF的面积。
6.B
一种商品按原价的八五折出售,降价后的价格是原价的85%。
故答案为:B。
打几折,即按原价的十分之几、百分之几十出售,打八五折即按原价的出售,化成百分数即可(分数分子上的数后面加%即可)。
7.D
解:4×n+1×1×2=(4n+2)(平方厘米)。
故答案为:D。
正方体一个面的面积=棱长×棱长=1×1=1平方厘米;n(n为大于0的自然数)个这样的正方体摆成的长方体的表面积=(4n+2)。
8.D
解:4+4×π÷4=4+π。
故答案为:D。
将一个圆形纸片对折两次得到的扇形占整个圆的,这个扇形的周长=圆的直径+圆的周长÷4;其中,圆的周长=π×直径。
9.B
解:12÷4=3(厘米)
3×3=9(平方厘米)
36÷9=4
4=2×2,按照2:1放大的。
故答案为:B。
正方形的面积=边长×边长,先计算原来正方形的面积,现在正方形的面积是原来正方形面积的4倍,4=2×2,按照2:1放大的。
10.A
解:6×8÷2×2÷10
=48÷10
=4.8。
故答案为:A。
直角三角形较短的两条边直角边分别是它的底和高,这个三角形最长边上的高=直角三角形两条直角边的积÷2×2÷最长边的长度。
11.正确
解:一个自然数不是奇数就是偶数,原题说法正确.
故答案为:正确
奇数是末尾数字是1、3、5、7、9的数,偶数是末尾数字是0、2、4、6、8的数;注意0是偶数.由此判断即可.
12.正确
解:(4+4):(3+3)=8÷6=,比值不变,原题干说法正确。
故答案为:正确。
4:3的前项加上4,后项加上3,实际是比的前项和后项同时乘2,则比值不变。
13.错误
解:1×(1+10%)×(1-10%)
=1.1×0.9
=99%
99%<1,现价比原价低。
故答案为:错误。
把这件产品的原价看作单位“1”,现价=原价×(1+涨价的百分率)×(1-降价的百分率),然后比较大小。
14.错误
解:甲和乙的速度比是6:5,原题干说法错误。
故答案为:错误。
甲和乙的速度比=所用时间的反比。
15.错误
解:甲绳子的原长:米+米=米
乙绳子的原长:米+米=米
米≠米,这两根绳子原来不一样长
故答案为:错误。
甲绳剩下的长度+剩下的长度=甲绳原来的长度;乙绳剩下的长度+米=乙绳原来的长度;据此解答。
16.5:4
解:乙数:丙数=3:2=(3×2):(2×2)=6:4
所以甲数:乙数:丙数=5:6:4
甲数和丙数的比是5:4;
故答案为:5:4。
要想求甲数和丙数的比,需要将这两个比化成连比,两个比中都有乙数,对应的份数分别是6和3,而6和3的最小公倍数是6,因此,可以根据比的基本性质将乙数和丙数的比的前、后项同时乘2,即可写成连比,从而得到甲数和丙数的比。
17.37.5
解:6÷(6+10)
=6÷16
=37.5%。
故答案为:37.5。
盐占盐水的分率=盐的质量÷(盐的质量+水的质量) 。
18.;
解:1÷6=
5÷6=(千克)。
故答案为:;。
每人占的分率=1÷平均分的人数;每人分的质量=大米的总质量÷平均分的人数。
19.3.14;3.01;30%
解:30%=0.3,所以3.14>3.01>30%。
故答案为:3.14;3.01;30%。
百分数化成小数,把百分号去掉,小数点向左移动两位;然后比较大小。
20.25
解:a:b=4:5
20:b=4:5
4b=100
b=100÷4
b=25。
故答案为:25。
把a=20,代入比例中,应用比例的基本性质解比例。
21.2
解:由比例的基本性质可知A:B=1.2:=2。
故答案为:2。
比例的基本性质:两个外项的积等于两个内项的积。
22.340立方厘米;1020立方厘米
解:85×12×=340(立方厘米),所以圆锥的体积是340立方厘米;340×3=1020(立方厘米),所以与它等底等高的圆柱体积是1020立方厘米。
故答案为:340立方厘米;1020立方厘米。
圆锥的体积=底面积×高×;
等底等高圆柱的体积是圆锥体积的3倍。
23.62.5;60;40;25
解:5÷8×100%=62.5%
(8-5)÷5×100%
=3÷5×100%
=60%
50×(1-20%)
=50×80%
=40(kg)
35÷(1+40%)
=35÷140%
=25(m)
故答案为:62.5;60;40;25。
求一个数是另一个数的百分之几,这个数÷另一个数×100%;
求一个数比另一个数多(少)百分之几,大数-小数=多的(少的),(大数-小数)÷单位“1”×100%=多(少)百分之几;
已知一个数比另一个数多(少)百分之几:1+多百分之几=比较量占单位“1”的百分之几,单位“1”的量×(1+多百分之几)=比较量,1-少百分之几=比较量占单位“1”的百分之几,单位“1”的量×(1-少百分之几)=比较量。
24.36.4
解:如图所示,因为两个图形都是正方形,因此∠D=∠OCF=90°,且AD∥CF,所以∠DAO=∠OFC,而∠AOD=∠FOC,因此△ADO∽△FCO,所以。
设CO=x厘米,则OG=(4-x)厘米,DG=6-4=2厘米,因此,变形为6x=4(2+4-x),即6x=24-4x,解得x=2.4,OD=6-2.4=3.6厘米。S△ADO=6×3.6÷2=10.8(平方厘米),S△FCO=4×2.4÷2=4.8(平方厘米),S阴影面积=6×6+4×4-10.8-4.8=36.4(平方厘米)。
故答案为:36.4。
本题求阴影部分面积,观察图形可以看到阴影部分是两个梯形,而空白区域是两个三角形,很明显这两个三角形相似,此时需要证明出这两个三角形相似即可。三角形相似,则有,这时可以设CO=x厘米,比例形式就转换为未知数方程求解,自然可以解出CO和OD的值,这样三角形的底和高都有,根据三角形面积计算公式“底乘以高除以二”,两个面积也能求出,然后用两个正方形面积之和减去这两个三角形面积,就是阴影部分面积。
25.240
解:设圆柱的体积是x立方厘米。
(1-)x+x=13×10×2
x=260
x=260÷
x=240。
故答案为:240。
等底等高的圆锥的体积是圆柱体积的,依据等量关系式:(1-圆柱露出的高度)×圆柱的体积+×圆柱的体积=长方体的长×宽×上升水的高度,列方程,解方程。
26.
16.5÷10%=165 1-+= 1.05×=0.6 ×÷×=
1-0.62=0.64 -×= 1.5a-a=0.5a 0.9×9.9+0.09=9
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.①x+36=100
解: x=100-36
x=64
②0.3x+3.2×5=22
解:0.3x+16=22
0.3x=6
x=6÷0.3
x=20
③0.35:=x:6
解: x=0.35×6
x=2.1
x=2.1÷
x=3.5
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①应用等式的性质1解方程;
②综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积;
③应用比例的基本性质解比例。
28.(1)东;北;60;4
(2)解:
(3)9.87
(4)解:
解:(1)1×4=4(厘米),点P在点M的东偏北60°方向4厘米处;
(3)6×4-3.14×32÷2
=24-14.13
=9.87(平方厘米)。
故答案为:(1)东;北;60;4;(3)9.87。
(1)等边三角形每个内角是60°,三条边都相等,边长=1×格数=4厘米;在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)图中阴影部分的面积=长方形的长×宽-π×半径2÷2;
(4)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
29.解:A店:80×0.7=56(元)
B店:80-19=61(元)
答:在A书店买应付56元,在B书店买应付61元。
A店应付钱数=原价×折扣,B店应付钱数=原价-减少的钱数,据此解答。
30.解:10000×3.87%×5= 1935 (元)
答:到期后陈老师可以拿出1935元来资助贫困生。
利息=本金×利率×存期。
31.解:(520+4×50)÷(4+5)
=720÷9
=80(元)
80-50=30(元)
答:一个篮球30元,一个足球80元。
把4个篮球看作4个足球,则总钱数=原来买4个篮球和5个足球的总钱数+4×每个篮球比每个足球便宜的钱数,则足球的单价=把4个篮球看作4个足球的总钱数÷(4+5)=80元,篮球的单价=足球的单价-50元。
32.解:45÷2=(cm)
设BC的长为xcm,则CD的长为(-x)cm。
7x=(-x)×8
15x=180
x=180÷15
x=12
12×7=84(cm2)
答:平行四边形的面积为84cm2。
平行四边形的面积=底×高;依据面积相等列方程,求出底、高的长度。
33.解:
设原来乘客的人数为x人,
5+x=15
x=10
x=10÷
x=50
5+50=55(个)
答:这辆大客车一共有55个乘客座位。
依据等量关系式:出发时车上还有空座位的个数+×这辆大客车一共有乘客座位的个数=又上车的人数,列方程,解方程。
34.解:()×8
=
=
1-=
÷=10(天)
答:还需要10天完成。
乙队单独修还需要的天数=(1-甲、乙工作效率的和×合修的时间)÷乙的工作效率。
35.解:10×10×6.28=628(立方厘米)
628÷(10÷2)2÷3.14
=200÷25
=8(厘米)
答:此时水深8厘米。
水的体积=底面积×水的高度;水在圆柱中的深度=水的体积÷圆柱底面积。
同课章节目录
