期末测试卷(含答案)---2024-2025学年六年级数学下册(苏教版)
文档属性
| 名称 | 期末测试卷(含答案)---2024-2025学年六年级数学下册(苏教版) |  | |
| 格式 | docx | ||
| 文件大小 | 193.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 07:39:37 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级下册期末测试卷(苏教版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.一个圆柱容器底面积是高20cm,原来水面高度是8cm,往容器内浸没物体后,水面高度均上升至10cm,下面说法错误的是( )。
A.正方体、圆锥、圆柱的体积相同
B.圆锥的体积是
C.圆锥的高度是圆柱的3倍
D.三个物体全部浸入一个容器,水不会溢出
2.小李加工一批零件,工作时间与加工零件的个数的关系(如下图),下列说法错误的是( )
A.加工零件的个数与工作时间成正比例关系
B.N表示400个零件
C.M表示3.2小时
D.如果有一点Р表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上
3.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?( )
A.国债 B.理财产品 C.一样大 D.无法确定
4.学校在小明家北偏东30°方向上,则小明家在学校的( )方向上。
A.东偏北30° B.南偏西30° C.西偏南30° D.南偏西60°
5.下列四组概念,具有如下图这样关系的是( )。
A.平行四边形、长方形、正方形
B.长方体、圆柱、圆锥
C.三角形、等腰三角形、直角三角形
D.长方体、长方形、正方形
6.下面各组中的两个量,成反比例关系的是( )。
A.一个圆的半径和它的面积
B.看一本书,每天看的页数和看完的天数
C.一个圆的周长和直径
D.买同一种苹果,买的数量与付的金额
7.把1000元钱存银行,存两年的年利率是2.45%,两年后再到的本息是多少,正确的算式是( )。
A. B.
C. D.
8.把分别写有11、12、13、14…18、19、20的10张卡片反扣在桌面上,打乱顺序后,任意摸出1张,摸到( )的可能性最小。
A.奇数 B.偶数 C.质数 D.合数
9.升入中学,我们将会学习这样的知识:“三个角分别相等,三边成比例的两个三角形叫做相似三角形。”在小学,我们可以看作是“图形的放大和缩小”。根据你的理解,下图中( )两个三角形相似。
A.①和② B.①和③ C.①和④ D.②和④
10.海警船正在巡逻时,接收到一艘渔船发出的求助信息:雷达显示,你们(海警船)在我们渔船的北偏东40°方向5海里处。因我船故障无法航行,请求帮助。海警船立即开展救援行动,应该向( )方向航行5海里。
A.南偏西40° B.南偏东40° C.北偏东40° D.北偏西40°
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.一辆车的车轮大小一定,这辆车所行的路程和车轮的转数成正比例。( )
12.人的年龄与身高成正比例。( )
13.某零件长7.2mm,画在图纸上长36cm,这幅图的比例尺是50∶1。
14.圆柱底面的半径是1cm,高也是3.14cm,它的侧面展开图是一个正方形。
15.绘制某地区一年内月平均气温的变化情况,应该选择折线统计图,因为折线统计图能清楚地反映出气温的变化情况。
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一根长100cm的圆柱形木料,沿着木料横截成长短不同的3个圆柱形,表面积增加,这根圆柱形木料原来一共的体积是 。
17.一件商品打六折销售。“六折”表示销售价是原价的 %。如果销售价是150元;那么销售价比原价便宜 元。
18.一种袋装食品,超过标准净重的部分记为正数,不足部分记为负数。一袋食品净重104克,记为﹢4克,那么这种食品的标准净重是 克:记为﹣3克的食品净重为 克。
19.给左边四个图形分类。甲同学把①②分为一类。③④分为一类。这样分类的理由是 ;乙同学把①②③分为一类,④为一类。这样分类的理由是 。
20.如图这样的两个长方体叠在一起,叠起来的图形体积是 立方厘米,表面积最小是 平方厘米。
21.足球比赛中,若胜一场记作3分,平一场记作1分,负一场记作分,则胜三场记作 分,平一场负两场记作 分。
22.如图,一个表面涂满了颜料的长方体盒子平放在桌面上(图1),它相邻的三条棱长分别是5cm,4cm,2cm。现将它沿最长的棱翻转一次(图2),接着又沿最长的棱翻转一次(图3),接着又沿最长的棱翻转一次……,这样一共翻转了10次后拿走盒子,这时桌面上留下了颜料的印迹总面积是 cm2。(不计颜料消耗)
23.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有 人。
24.如果和互为倒数,且=,那么a= 。和成 比例关系。
25.在一次投掷测试中,及格线是15m,小明投了18m,老师记为“﹢3m”,那么小红投了14.5m,就记为 m。
阅卷人 四、计算题(20分)
得分
26.求未知数x。
(1)2.4∶x=4∶3 (2)x+10%x=0.45 (3)0.4×(12-x)=1.6
27.解方程。
0.25∶=15∶100 -9=21
阅卷人 五、操作题(10分)
得分
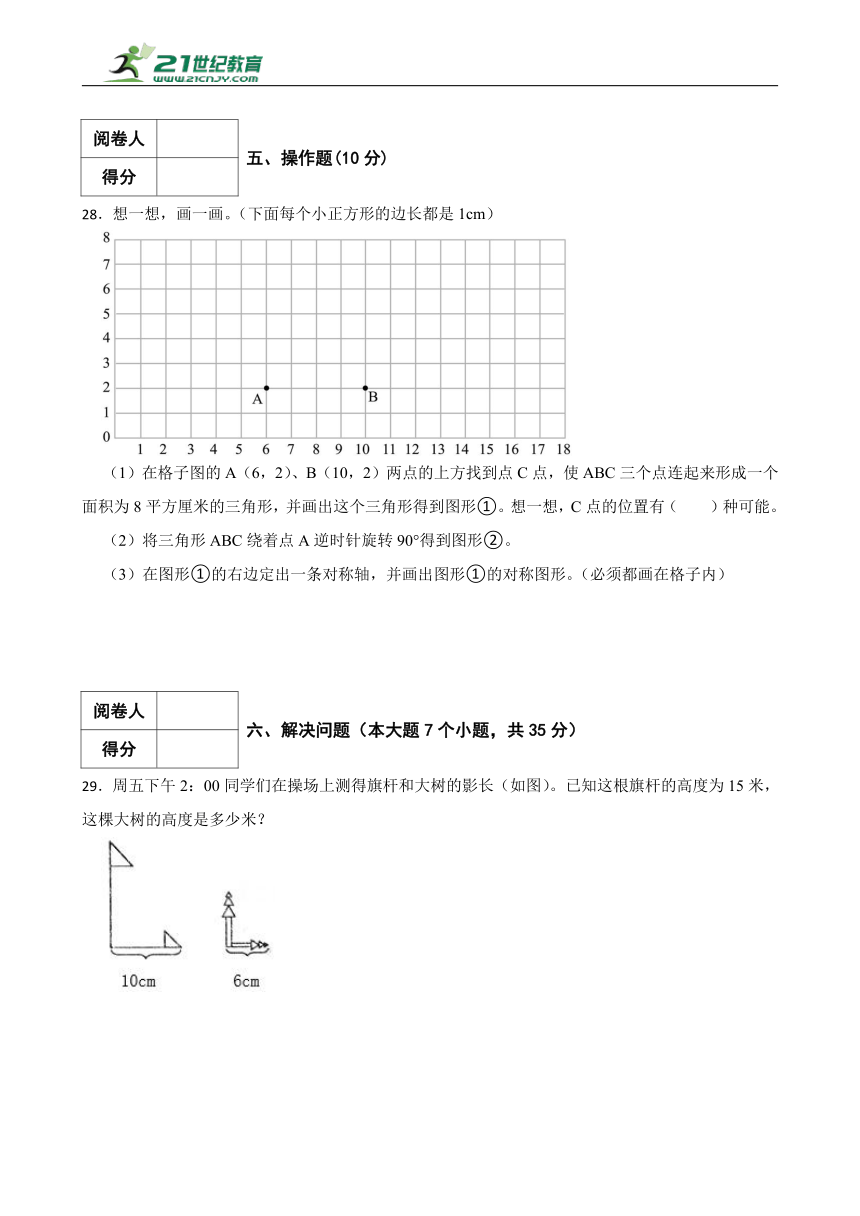
28.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.周五下午2:00同学们在操场上测得旗杆和大树的影长(如图)。已知这根旗杆的高度为15米,这棵大树的高度是多少米?
30. 一个圆锥形的沙堆,底面积是37.68m2,高是3m。用这堆沙在10米宽的公路上铺3cm厚的路面,能铺多少米长的路?
31.如图是星光小学六年级学生参加社团的情况。(每人只选一个)
(1)参加机器人社团和合唱社团的人数和占总人数的 %。
(2)如果该小学六年级共有300人,参加航模社团的人数比参加舞蹈社团的多多少人?
32.煤矿的空地上有一堆近似圆锥体形状的煤。已知煤堆的底面积是 50.24m2,高是2.1m。现准备用一辆车厢容积为6m3的车来运,至少需要运多少次才能运完?
33.小丽爸爸做了一个圆柱形的钢化玻璃鱼缸(无盖),这个鱼缸的底面半径是20cm,高是30cm(如图)
(1)做这样一个鱼缸,至少需要多少平方厘米的钢化玻璃?
(2)在做好的鱼缸里倒入20cm高的水,小丽将一块珊瑚石放人鱼缸并完全浸没后,发现水面升高了5cm,这块珊瑚石的体积是多少立方分米?(鱼缸厚度忽略不计)
34. 一个圆锥形麦堆,已知高与底面直径的和是9米,且高与底面直径的比是1:2。
(1)分别求出圆锥形麦堆的高与底面直径。
(2)如果每立方米小麦重750千克,这堆小麦重多少千克?
答案解析部分
1.C
解:A:水面都是升高了2厘米,说明正方体、圆锥、圆柱的体积相同 ,原题说法正确;
B:240×(10-8)=480(立方厘米),圆锥的体积是,原题说法正确;
C:不知道圆柱圆锥的底面积,不能判断圆锥的高度是不是圆柱的3倍 ,原题说法错误;
D:2+2+2+8=14(厘米),14厘米<20厘米,三个物体全部浸入一个容器,水不会溢出 ,原题说法正确。
故答案为:C。
圆柱容器底面积×水面上升的高度=浸没物体的体积。
2.D
解:A项:150÷1.5=100(个)(一定)加工零件的个数与工作时间成正比例关系,原题干说法正确;
B项:4×100=400(个),原题干说法正确;
C项:320÷100=3.2(小时),原题干说法正确;
D项:600÷5=120(个),120>100,点P不和点E、F、G一样在射线上,原题干说法错误。
故答案为:D。
A项:点O、E、F、G一样在同一条射线上,说明加工零件的个数与工作时间成正比例关系;
B项:N表示加工零件的个数=平均每小时加工零件的个数×加工的时间;
C项:M表示的时间= 加工零件的总个数÷平均每小时加工零件的个数;
D项:平均每小时加工零件的个数不是120,说明点P不和点E、F、G一样在射线上。
3.B
接:买国债:2×3×4%=0.24万元;买理财产品:2×1×4%=0.08万元,(2+0.08)×1×4%=0.0832万元,(2+0.08+0.0832)×1×4%=0.086528万元,0.08+0.0832+0.086528=0.249728万元。
0.24<0.249728,所以理财产品这种理财方式收益更大。
故答案为:B。
买国债获得的利息=爸爸有的钱数×存期×年利率;
买理财产品第一年获得的利息=爸爸有的钱数×1×年收益率,买理财产品第二年获得的利息=(爸爸有的钱数+买理财产品第一年获得的利息)×1×年收益率,买理财产品第三年获得的利息=(爸爸有的钱数+买理财产品第一年获得的利息+买理财产品第二年获得的利息)×1×年收益率;
然后把买理财产品的三年的利息加起来与买国债获得的利息比较即可。
4.B
5.A
6.B
7.C
8.C
9.C
10.A
11.正确
解:一辆车的车轮大小一定,这辆车所行的路程和车轮的转数成正比例。原题说法正确。
故答案为:正确。
路程÷车轮的转数=车轮的周长(一定),相关联的两个量的比值一定,所以二者成正比例。
12.错误
13.√
14.×
15.√
16.1250
17.60;100
18.100;97
19.按底面是四边形和圆形分类(答案不唯一);按柱体和锥体分类(答案不唯一)
20.112;144
21.9;﹣3
22.170
23.48
解:16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48。
故答案为:48。
每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。用分解质因数的方法求出16和12的最小公倍数是:2×2×2×2×3=48。
24.;反
解:由和互为倒数,可知=1;
由=可得出:=6a
把=1代入=6a中,即1=6a,那么a=。
因为=1(一定),即乘积一定,所以和成反比例关系。
故答案为:;反。
乘积是1的两个数互为倒数,然后把xy=1代入计算,判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
25.﹣0.5
26.(1)x=1.8;(2)x=;(3)x=8
27.=;=100
28.解:(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(2)、(3)
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。三角形的面积=底×高÷2,以线段AB为一条边,画出面积为8平方厘米的三角,则点C的位置有无数种可能,据此画图;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可。
(3)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
29.解:设这棵大树的高度是x厘米。15米=1500厘米。
1500:10=x:6
10x=1500×6
x=9000÷10
x=900
900厘米=9米
答:这棵大树的高度是9米。
同一时间、同一地点,高度与影子长度的比相等。由此设这棵大树的高度是x厘米。根据旗杆高度与影子长度的比与大树高度与影子长度的比相等列出比例解答即可。注意换算单位。
30.解:3厘米=0.03米,
37.68×3÷3÷(10×0.03)
=37.68÷0.3
=125.6(米);
答:能铺125.6米长的路。
圆锥的体积=底面积×高÷3,长方体的体积=长×宽×高,根据题意,先求出圆锥形沙堆的体积,再除以路面的宽和厚度,即可求出能铺路的长度。
31.(1)57
(2)300×(20%-13%)
=300×7%
=21(人)
答:参加航模社团的人数比参加舞蹈社团的多21人。
解:(1)1-20%-13%-10%=57%
故答案为:(1)57。
(1)总人数是“1”,用1减去航模组、舞蹈组、演讲组占总人数的百分率即可求出机器人社团和合唱社团占总人数的百分率;
(2)用总人数乘参加航模社团比参加舞蹈社团多的占总人数的百分率即可求出参加航模社团的人数比参加舞蹈社团多的人数。
32.解:50.24×2.1÷3=35.168(立方米)
35.168÷6≈6(次)
答:至少需要运6次才能运完。
圆锥的体积=底面积×高÷3;圆锥的体积÷一辆车厢的容积,商采取进一法得到的整数就是至少运的次数。
33.(1)解:3.14×20×2×30+3.14×202
=3.14×1200+3.14×400
=3.14×1600
=5024 (cm2)
答:至少需要5024cm2的钢化玻璃。
(2)解:3.14×202×5
=3.14×2000
=6280(cm3)
6280 cm3= 6.28 dm3
答:这块珊瑚石的体积是6.28 dm3。
(1)根据圆面积公式计算底面积,用圆柱的底面周长乘高求出侧面积,底面积加上侧面积就是需要钢化玻璃的面积;
(2)水面升高部分水的体积就是珊瑚石的体积,因此用圆柱的底面积乘水面上升的高度即可求出这块珊瑚石的体积。
34.(1)解:高:9×=9×=3(米)
底面直径:9-3=6(米)
答:高是3米,底面直径是6米。
(2)解:底面半径:6÷2=3(米)
3.14×3×3×3÷3×750
=28.26×750
=21195(千克)
答:这堆小麦重21195千克。
(1)高与底面直径的和×高占高与底面直径的和的分率=圆锥的高,高与底面直径的和-高=直径;
(2)π×底面半径的平方×高÷3=圆锥的体积,圆锥的体积×每立方米小麦重=这堆小麦重。
2024-2025学年六年级下册期末测试卷(苏教版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.一个圆柱容器底面积是高20cm,原来水面高度是8cm,往容器内浸没物体后,水面高度均上升至10cm,下面说法错误的是( )。
A.正方体、圆锥、圆柱的体积相同
B.圆锥的体积是
C.圆锥的高度是圆柱的3倍
D.三个物体全部浸入一个容器,水不会溢出
2.小李加工一批零件,工作时间与加工零件的个数的关系(如下图),下列说法错误的是( )
A.加工零件的个数与工作时间成正比例关系
B.N表示400个零件
C.M表示3.2小时
D.如果有一点Р表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上
3.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?( )
A.国债 B.理财产品 C.一样大 D.无法确定
4.学校在小明家北偏东30°方向上,则小明家在学校的( )方向上。
A.东偏北30° B.南偏西30° C.西偏南30° D.南偏西60°
5.下列四组概念,具有如下图这样关系的是( )。
A.平行四边形、长方形、正方形
B.长方体、圆柱、圆锥
C.三角形、等腰三角形、直角三角形
D.长方体、长方形、正方形
6.下面各组中的两个量,成反比例关系的是( )。
A.一个圆的半径和它的面积
B.看一本书,每天看的页数和看完的天数
C.一个圆的周长和直径
D.买同一种苹果,买的数量与付的金额
7.把1000元钱存银行,存两年的年利率是2.45%,两年后再到的本息是多少,正确的算式是( )。
A. B.
C. D.
8.把分别写有11、12、13、14…18、19、20的10张卡片反扣在桌面上,打乱顺序后,任意摸出1张,摸到( )的可能性最小。
A.奇数 B.偶数 C.质数 D.合数
9.升入中学,我们将会学习这样的知识:“三个角分别相等,三边成比例的两个三角形叫做相似三角形。”在小学,我们可以看作是“图形的放大和缩小”。根据你的理解,下图中( )两个三角形相似。
A.①和② B.①和③ C.①和④ D.②和④
10.海警船正在巡逻时,接收到一艘渔船发出的求助信息:雷达显示,你们(海警船)在我们渔船的北偏东40°方向5海里处。因我船故障无法航行,请求帮助。海警船立即开展救援行动,应该向( )方向航行5海里。
A.南偏西40° B.南偏东40° C.北偏东40° D.北偏西40°
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.一辆车的车轮大小一定,这辆车所行的路程和车轮的转数成正比例。( )
12.人的年龄与身高成正比例。( )
13.某零件长7.2mm,画在图纸上长36cm,这幅图的比例尺是50∶1。
14.圆柱底面的半径是1cm,高也是3.14cm,它的侧面展开图是一个正方形。
15.绘制某地区一年内月平均气温的变化情况,应该选择折线统计图,因为折线统计图能清楚地反映出气温的变化情况。
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.一根长100cm的圆柱形木料,沿着木料横截成长短不同的3个圆柱形,表面积增加,这根圆柱形木料原来一共的体积是 。
17.一件商品打六折销售。“六折”表示销售价是原价的 %。如果销售价是150元;那么销售价比原价便宜 元。
18.一种袋装食品,超过标准净重的部分记为正数,不足部分记为负数。一袋食品净重104克,记为﹢4克,那么这种食品的标准净重是 克:记为﹣3克的食品净重为 克。
19.给左边四个图形分类。甲同学把①②分为一类。③④分为一类。这样分类的理由是 ;乙同学把①②③分为一类,④为一类。这样分类的理由是 。
20.如图这样的两个长方体叠在一起,叠起来的图形体积是 立方厘米,表面积最小是 平方厘米。
21.足球比赛中,若胜一场记作3分,平一场记作1分,负一场记作分,则胜三场记作 分,平一场负两场记作 分。
22.如图,一个表面涂满了颜料的长方体盒子平放在桌面上(图1),它相邻的三条棱长分别是5cm,4cm,2cm。现将它沿最长的棱翻转一次(图2),接着又沿最长的棱翻转一次(图3),接着又沿最长的棱翻转一次……,这样一共翻转了10次后拿走盒子,这时桌面上留下了颜料的印迹总面积是 cm2。(不计颜料消耗)
23.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有 人。
24.如果和互为倒数,且=,那么a= 。和成 比例关系。
25.在一次投掷测试中,及格线是15m,小明投了18m,老师记为“﹢3m”,那么小红投了14.5m,就记为 m。
阅卷人 四、计算题(20分)
得分
26.求未知数x。
(1)2.4∶x=4∶3 (2)x+10%x=0.45 (3)0.4×(12-x)=1.6
27.解方程。
0.25∶=15∶100 -9=21
阅卷人 五、操作题(10分)
得分
28.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
阅卷人 六、解决问题(本大题7个小题,共35分)
得分
29.周五下午2:00同学们在操场上测得旗杆和大树的影长(如图)。已知这根旗杆的高度为15米,这棵大树的高度是多少米?
30. 一个圆锥形的沙堆,底面积是37.68m2,高是3m。用这堆沙在10米宽的公路上铺3cm厚的路面,能铺多少米长的路?
31.如图是星光小学六年级学生参加社团的情况。(每人只选一个)
(1)参加机器人社团和合唱社团的人数和占总人数的 %。
(2)如果该小学六年级共有300人,参加航模社团的人数比参加舞蹈社团的多多少人?
32.煤矿的空地上有一堆近似圆锥体形状的煤。已知煤堆的底面积是 50.24m2,高是2.1m。现准备用一辆车厢容积为6m3的车来运,至少需要运多少次才能运完?
33.小丽爸爸做了一个圆柱形的钢化玻璃鱼缸(无盖),这个鱼缸的底面半径是20cm,高是30cm(如图)
(1)做这样一个鱼缸,至少需要多少平方厘米的钢化玻璃?
(2)在做好的鱼缸里倒入20cm高的水,小丽将一块珊瑚石放人鱼缸并完全浸没后,发现水面升高了5cm,这块珊瑚石的体积是多少立方分米?(鱼缸厚度忽略不计)
34. 一个圆锥形麦堆,已知高与底面直径的和是9米,且高与底面直径的比是1:2。
(1)分别求出圆锥形麦堆的高与底面直径。
(2)如果每立方米小麦重750千克,这堆小麦重多少千克?
答案解析部分
1.C
解:A:水面都是升高了2厘米,说明正方体、圆锥、圆柱的体积相同 ,原题说法正确;
B:240×(10-8)=480(立方厘米),圆锥的体积是,原题说法正确;
C:不知道圆柱圆锥的底面积,不能判断圆锥的高度是不是圆柱的3倍 ,原题说法错误;
D:2+2+2+8=14(厘米),14厘米<20厘米,三个物体全部浸入一个容器,水不会溢出 ,原题说法正确。
故答案为:C。
圆柱容器底面积×水面上升的高度=浸没物体的体积。
2.D
解:A项:150÷1.5=100(个)(一定)加工零件的个数与工作时间成正比例关系,原题干说法正确;
B项:4×100=400(个),原题干说法正确;
C项:320÷100=3.2(小时),原题干说法正确;
D项:600÷5=120(个),120>100,点P不和点E、F、G一样在射线上,原题干说法错误。
故答案为:D。
A项:点O、E、F、G一样在同一条射线上,说明加工零件的个数与工作时间成正比例关系;
B项:N表示加工零件的个数=平均每小时加工零件的个数×加工的时间;
C项:M表示的时间= 加工零件的总个数÷平均每小时加工零件的个数;
D项:平均每小时加工零件的个数不是120,说明点P不和点E、F、G一样在射线上。
3.B
接:买国债:2×3×4%=0.24万元;买理财产品:2×1×4%=0.08万元,(2+0.08)×1×4%=0.0832万元,(2+0.08+0.0832)×1×4%=0.086528万元,0.08+0.0832+0.086528=0.249728万元。
0.24<0.249728,所以理财产品这种理财方式收益更大。
故答案为:B。
买国债获得的利息=爸爸有的钱数×存期×年利率;
买理财产品第一年获得的利息=爸爸有的钱数×1×年收益率,买理财产品第二年获得的利息=(爸爸有的钱数+买理财产品第一年获得的利息)×1×年收益率,买理财产品第三年获得的利息=(爸爸有的钱数+买理财产品第一年获得的利息+买理财产品第二年获得的利息)×1×年收益率;
然后把买理财产品的三年的利息加起来与买国债获得的利息比较即可。
4.B
5.A
6.B
7.C
8.C
9.C
10.A
11.正确
解:一辆车的车轮大小一定,这辆车所行的路程和车轮的转数成正比例。原题说法正确。
故答案为:正确。
路程÷车轮的转数=车轮的周长(一定),相关联的两个量的比值一定,所以二者成正比例。
12.错误
13.√
14.×
15.√
16.1250
17.60;100
18.100;97
19.按底面是四边形和圆形分类(答案不唯一);按柱体和锥体分类(答案不唯一)
20.112;144
21.9;﹣3
22.170
23.48
解:16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48。
故答案为:48。
每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。用分解质因数的方法求出16和12的最小公倍数是:2×2×2×2×3=48。
24.;反
解:由和互为倒数,可知=1;
由=可得出:=6a
把=1代入=6a中,即1=6a,那么a=。
因为=1(一定),即乘积一定,所以和成反比例关系。
故答案为:;反。
乘积是1的两个数互为倒数,然后把xy=1代入计算,判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
25.﹣0.5
26.(1)x=1.8;(2)x=;(3)x=8
27.=;=100
28.解:(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(2)、(3)
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。三角形的面积=底×高÷2,以线段AB为一条边,画出面积为8平方厘米的三角,则点C的位置有无数种可能,据此画图;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可。
(3)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
29.解:设这棵大树的高度是x厘米。15米=1500厘米。
1500:10=x:6
10x=1500×6
x=9000÷10
x=900
900厘米=9米
答:这棵大树的高度是9米。
同一时间、同一地点,高度与影子长度的比相等。由此设这棵大树的高度是x厘米。根据旗杆高度与影子长度的比与大树高度与影子长度的比相等列出比例解答即可。注意换算单位。
30.解:3厘米=0.03米,
37.68×3÷3÷(10×0.03)
=37.68÷0.3
=125.6(米);
答:能铺125.6米长的路。
圆锥的体积=底面积×高÷3,长方体的体积=长×宽×高,根据题意,先求出圆锥形沙堆的体积,再除以路面的宽和厚度,即可求出能铺路的长度。
31.(1)57
(2)300×(20%-13%)
=300×7%
=21(人)
答:参加航模社团的人数比参加舞蹈社团的多21人。
解:(1)1-20%-13%-10%=57%
故答案为:(1)57。
(1)总人数是“1”,用1减去航模组、舞蹈组、演讲组占总人数的百分率即可求出机器人社团和合唱社团占总人数的百分率;
(2)用总人数乘参加航模社团比参加舞蹈社团多的占总人数的百分率即可求出参加航模社团的人数比参加舞蹈社团多的人数。
32.解:50.24×2.1÷3=35.168(立方米)
35.168÷6≈6(次)
答:至少需要运6次才能运完。
圆锥的体积=底面积×高÷3;圆锥的体积÷一辆车厢的容积,商采取进一法得到的整数就是至少运的次数。
33.(1)解:3.14×20×2×30+3.14×202
=3.14×1200+3.14×400
=3.14×1600
=5024 (cm2)
答:至少需要5024cm2的钢化玻璃。
(2)解:3.14×202×5
=3.14×2000
=6280(cm3)
6280 cm3= 6.28 dm3
答:这块珊瑚石的体积是6.28 dm3。
(1)根据圆面积公式计算底面积,用圆柱的底面周长乘高求出侧面积,底面积加上侧面积就是需要钢化玻璃的面积;
(2)水面升高部分水的体积就是珊瑚石的体积,因此用圆柱的底面积乘水面上升的高度即可求出这块珊瑚石的体积。
34.(1)解:高:9×=9×=3(米)
底面直径:9-3=6(米)
答:高是3米,底面直径是6米。
(2)解:底面半径:6÷2=3(米)
3.14×3×3×3÷3×750
=28.26×750
=21195(千克)
答:这堆小麦重21195千克。
(1)高与底面直径的和×高占高与底面直径的和的分率=圆锥的高,高与底面直径的和-高=直径;
(2)π×底面半径的平方×高÷3=圆锥的体积,圆锥的体积×每立方米小麦重=这堆小麦重。
同课章节目录
