13.2.4平面与平面的垂直 课件(共30张PPT)2024-2025学年高一下学期数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.4平面与平面的垂直 课件(共30张PPT)2024-2025学年高一下学期数学苏教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 536.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 16:20:03 | ||
图片预览





文档简介
(共30张PPT)
新课程标准解读 核心素养
借助长方体,通过直观感知,了解空间中平面与平面垂直的判定定理与性质定理. 逻辑推理、
数学运算、
直观想象
平面与平面垂直
平面与平面垂直
一般地,如果两个平面所成的二面角是
直二面角,我们就说这两个平面垂直.
记作:
a
l
β
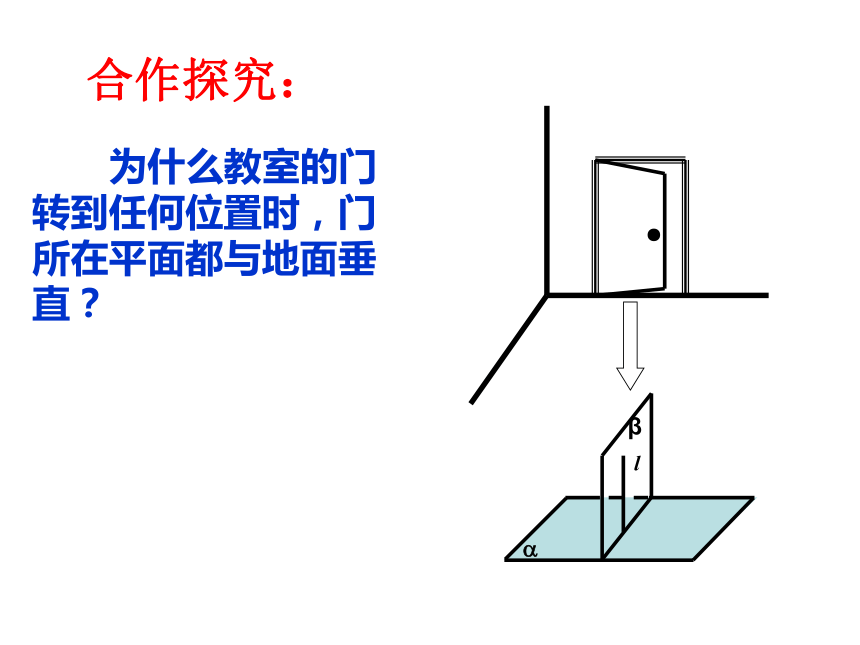
合作探究:
为什么教室的门转到任何位置时,门
所在平面都与地面垂直?
●
a
l
β
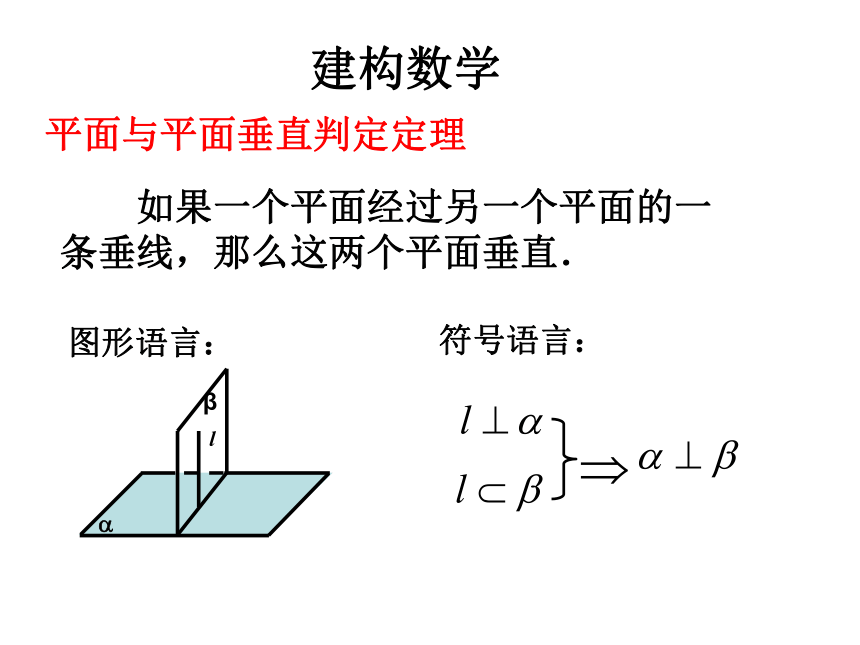
如果一个平面经过另一个平面的一
条垂线,那么这两个平面垂直.
平面与平面垂直判定定理
符号语言:
建构数学
a
l
β
图形语言:
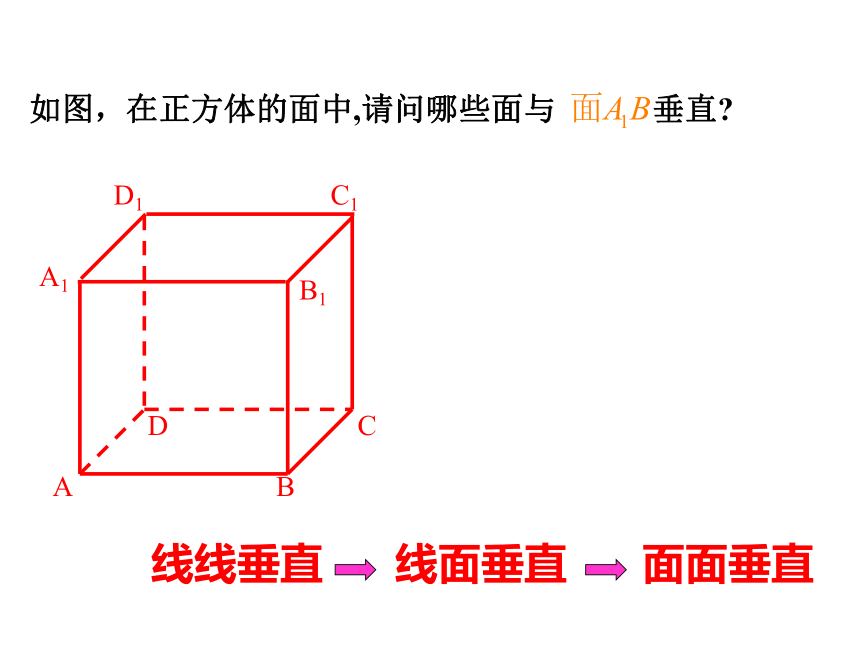
如图,在正方体的面中,请问哪些面与 垂直
面面垂直
线面垂直
线线垂直
A
B
C
D
A1
C1
B1
D1
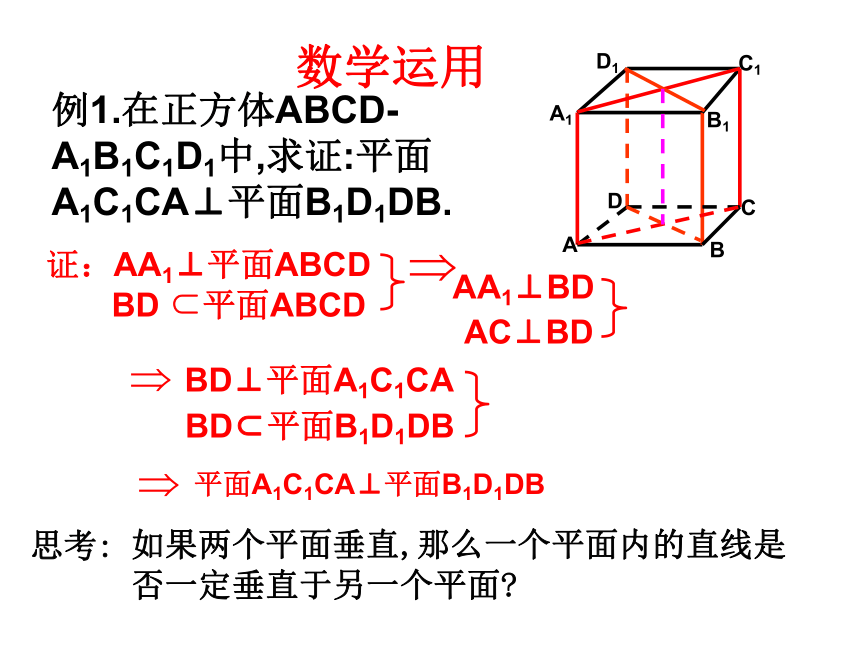
例1.在正方体ABCD-A1B1C1D1中,求证:平面A1C1CA⊥平面B1D1DB.
AA1⊥BD
BD⊥平面A1C1CA
平面A1C1CA⊥平面B1D1DB
数学运用
C
A1
C1
D1
B1
D
A
B
证:AA1⊥平面ABCD
BD 平面ABCD
AC⊥BD
BD 平面B1D1DB
思考:
如果两个平面垂直,那么一个平面内的直线是否一定垂直于另一个平面
找二面角的平面角
说明该平面角是直角。
(一般通过计算完成证明。)
面面垂直的判定方法:
1、定义法:
2、判定定理:
要证两个平面垂直,
另一个平面的一条垂线。
只要在其中一个平面内找到
(线面垂直 面面垂直)
M
A
E
D
B
C
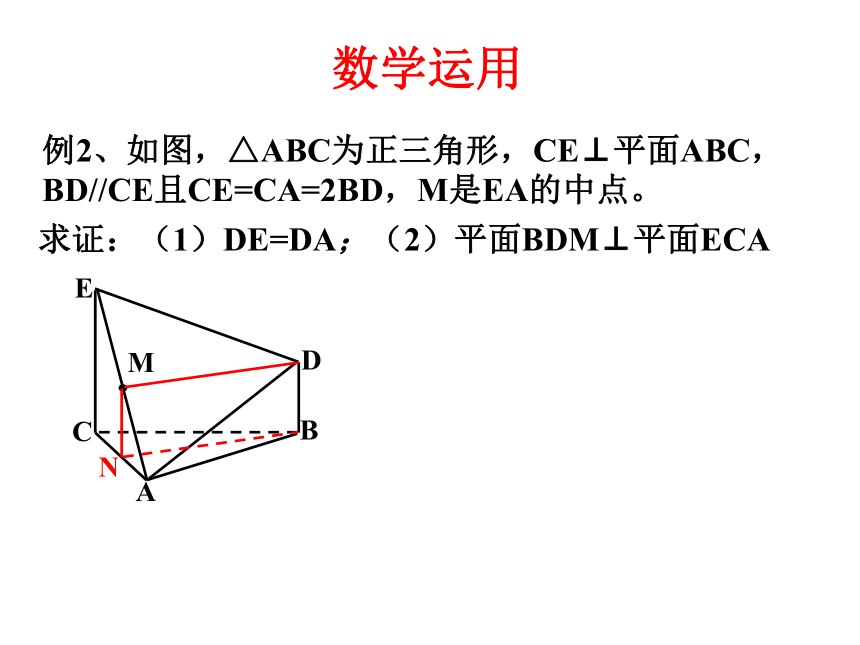
数学运用
例2、如图,△ABC为正三角形,CE⊥平面ABC,BD//CE且CE=CA=2BD,M是EA的中点。
求证:(1)DE=DA;(2)平面BDM⊥平面ECA
N
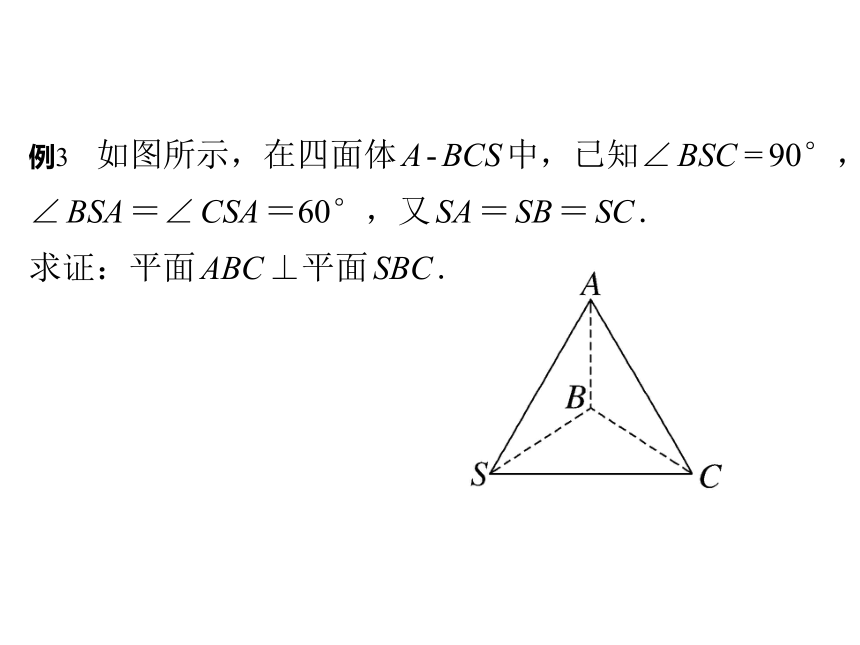
例3 如图所示,在四面体A-BCS中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明: 因为∠BSA=∠CSA
=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,
连接AD,SD,则AD⊥BC,SD⊥BC,
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
通性通法
证明面面垂直常用的方法
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂
直,即把问题转化为“线面垂直”;
A
B
C
D
A1
B1
C1
D1
练习3:在正方体ABCD-A1B1C1D1中,
求证:
课堂练习
P
A
B
C
O
课堂练习
练习4.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,
求证:
合作探究:
如果两个平面垂直,那么一个平面内的直线是否一定垂直于另一个平面?
要使一个平面内的一条直线垂直于另一个平面,须满足什么条件?
b
l
a
A
B
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
已知:a⊥b,a∩b=l,AB a,AB⊥l,B为垂足。
求证:AB⊥b。
分析:因为AB⊥l,所以要证AB⊥b,只需在b内找一条与l相交的直线垂直于AB。
平面与平面垂直的性质定理
C
b
a
b
P
例4.求证:如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内.
已知:a⊥b,P∈a,P∈a,a⊥b
求证:a a.
数学运用
l
b
a
b
P
l
b
a
a
P
已知:a⊥b,P∈a,P∈a,a⊥b
求证:a a.
数学运用
b
b
a
a
P
b
l
l
证:设a∩b=l
过点P在平面a内作直线b⊥l,
根据平面与平面垂直的性质定理,知b⊥b
因为经过一点有且只有一条直线与平面b垂直,
所以直线a与直线b重合,即a a。
练习:1.判断下列命题是否正确,并说明理由.
(1)若a⊥g,b⊥g ,则a∥b. ( )
(2)若a⊥b,b⊥g,则a⊥g. ( )
(3)若a∥a1, b∥b1,a⊥b,则a1⊥b1. ( )
2.如图,a⊥b,a∩b=l, AB a,AB⊥l,BC b,
DE b,BC⊥DE.
求证:AC⊥DE.
课堂练习
a
β
l
A
B
D
C
E
×
×
√
练习1 在正方体ABCD—A1B1C1D1中,
(1) 求证:平面A1C⊥平面B1D
A
C
D
A1
C1
D1
E
F
B
B1
(2) 若E、F分别是AB、BC的中点,
求证: 平面A1C1FE⊥平面B1D
(3) 若G是BB1的中点
求证:平面A1C1G⊥平面B1D
G
G
G
G
练习2 已知 α∩β=l,α⊥γ,β⊥γ.求证 l⊥γ.
α
β
γ
l
α
β
γ
l
P
E
F
α
β
γ
l
Q
P
课堂小结
一、二面角的定义
二、二面角的表示方法
三、二面角的平面角
四、二面角的平面角的作法
五、平面与平面垂直的判定定理☆
六、平面与平面垂直的性质定理☆
新课程标准解读 核心素养
借助长方体,通过直观感知,了解空间中平面与平面垂直的判定定理与性质定理. 逻辑推理、
数学运算、
直观想象
平面与平面垂直
平面与平面垂直
一般地,如果两个平面所成的二面角是
直二面角,我们就说这两个平面垂直.
记作:
a
l
β
合作探究:
为什么教室的门转到任何位置时,门
所在平面都与地面垂直?
●
a
l
β
如果一个平面经过另一个平面的一
条垂线,那么这两个平面垂直.
平面与平面垂直判定定理
符号语言:
建构数学
a
l
β
图形语言:
如图,在正方体的面中,请问哪些面与 垂直
面面垂直
线面垂直
线线垂直
A
B
C
D
A1
C1
B1
D1
例1.在正方体ABCD-A1B1C1D1中,求证:平面A1C1CA⊥平面B1D1DB.
AA1⊥BD
BD⊥平面A1C1CA
平面A1C1CA⊥平面B1D1DB
数学运用
C
A1
C1
D1
B1
D
A
B
证:AA1⊥平面ABCD
BD 平面ABCD
AC⊥BD
BD 平面B1D1DB
思考:
如果两个平面垂直,那么一个平面内的直线是否一定垂直于另一个平面
找二面角的平面角
说明该平面角是直角。
(一般通过计算完成证明。)
面面垂直的判定方法:
1、定义法:
2、判定定理:
要证两个平面垂直,
另一个平面的一条垂线。
只要在其中一个平面内找到
(线面垂直 面面垂直)
M
A
E
D
B
C
数学运用
例2、如图,△ABC为正三角形,CE⊥平面ABC,BD//CE且CE=CA=2BD,M是EA的中点。
求证:(1)DE=DA;(2)平面BDM⊥平面ECA
N
例3 如图所示,在四面体A-BCS中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
证明: 因为∠BSA=∠CSA
=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,
连接AD,SD,则AD⊥BC,SD⊥BC,
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
通性通法
证明面面垂直常用的方法
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂
直,即把问题转化为“线面垂直”;
A
B
C
D
A1
B1
C1
D1
练习3:在正方体ABCD-A1B1C1D1中,
求证:
课堂练习
P
A
B
C
O
课堂练习
练习4.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,
求证:
合作探究:
如果两个平面垂直,那么一个平面内的直线是否一定垂直于另一个平面?
要使一个平面内的一条直线垂直于另一个平面,须满足什么条件?
b
l
a
A
B
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
已知:a⊥b,a∩b=l,AB a,AB⊥l,B为垂足。
求证:AB⊥b。
分析:因为AB⊥l,所以要证AB⊥b,只需在b内找一条与l相交的直线垂直于AB。
平面与平面垂直的性质定理
C
b
a
b
P
例4.求证:如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内.
已知:a⊥b,P∈a,P∈a,a⊥b
求证:a a.
数学运用
l
b
a
b
P
l
b
a
a
P
已知:a⊥b,P∈a,P∈a,a⊥b
求证:a a.
数学运用
b
b
a
a
P
b
l
l
证:设a∩b=l
过点P在平面a内作直线b⊥l,
根据平面与平面垂直的性质定理,知b⊥b
因为经过一点有且只有一条直线与平面b垂直,
所以直线a与直线b重合,即a a。
练习:1.判断下列命题是否正确,并说明理由.
(1)若a⊥g,b⊥g ,则a∥b. ( )
(2)若a⊥b,b⊥g,则a⊥g. ( )
(3)若a∥a1, b∥b1,a⊥b,则a1⊥b1. ( )
2.如图,a⊥b,a∩b=l, AB a,AB⊥l,BC b,
DE b,BC⊥DE.
求证:AC⊥DE.
课堂练习
a
β
l
A
B
D
C
E
×
×
√
练习1 在正方体ABCD—A1B1C1D1中,
(1) 求证:平面A1C⊥平面B1D
A
C
D
A1
C1
D1
E
F
B
B1
(2) 若E、F分别是AB、BC的中点,
求证: 平面A1C1FE⊥平面B1D
(3) 若G是BB1的中点
求证:平面A1C1G⊥平面B1D
G
G
G
G
练习2 已知 α∩β=l,α⊥γ,β⊥γ.求证 l⊥γ.
α
β
γ
l
α
β
γ
l
P
E
F
α
β
γ
l
Q
P
课堂小结
一、二面角的定义
二、二面角的表示方法
三、二面角的平面角
四、二面角的平面角的作法
五、平面与平面垂直的判定定理☆
六、平面与平面垂直的性质定理☆
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
