数学:3.3.3《线性规划的实际应用》课件(新人教a版必修5)
文档属性
| 名称 | 数学:3.3.3《线性规划的实际应用》课件(新人教a版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-11 00:00:00 | ||
图片预览






文档简介
课件20张PPT。新课标人教版课件系列《高中数学》
必修53.3.3《线性规划的实际应用》审校:王伟教学目标1.知识目标:
会用线性规划的理论和方法解决一些较简单的实际问题;
2.能力目标:培养学生观察、分析、联想、以及作图的能力,渗透集合、化归、数形结合的数学思想,培养学生自主探究意识,提高学生“建模”和解决实际问题的能力;
3.情感目标:培养学生学习数学的兴趣和“用数学”的意识,激励学生创新,鼓励学生讨论,学会沟通,培养团结协作精神.
教学重点:把实际问题转化成线性规划问题,即建模,并给出解答.
教学难点:
1.建立数学模型.把实际问题转化为线性规划问题;
2.寻找整点最优解的方法.复习二元一次不等式表示的平面区域 在平面直角坐标系中,以二元一次方程x+y-1=0的解为坐标的点的集合{(x,y)|x+y-1=0}是经过点(0,1)和(1,0)的一条直线l,那么以二元一次不等式x+y-1>0的解为坐标的点的集合{(x,y)|x+y-1>0}是
什么图形? 探索结论 结论:二元一次不等式ax+by+c>0在平面直角坐标系中表示直线ax+by+c=0某一侧所有点组成的平面区域。不等式 ax+by+c<0表示的是另一侧的平面区域。x+y-1>0x+y-1<0复习判断二元一次不等式表示哪一侧平面区域的方法x+y-1>0x+y-1<0 由于对在直线ax+by+c=0同
一侧所有点(x,y),把它的坐标
(x,y)代入ax+by+c,所得的实
数的符号都相同,故只需在这条
直线的某一侧取一特殊点(x0,y0)
以ax0+by0+c的正负的情况便可
判断ax+by+c>0表示这一直线
哪一侧的平面区域,特殊地,当
c≠0时常把原点作为此特殊点复习线性规划问题:
设z=2x+y,式中变量满足
下列条件:
求z的最大值与最小值。 目标函数
(线性目标函数)线性约
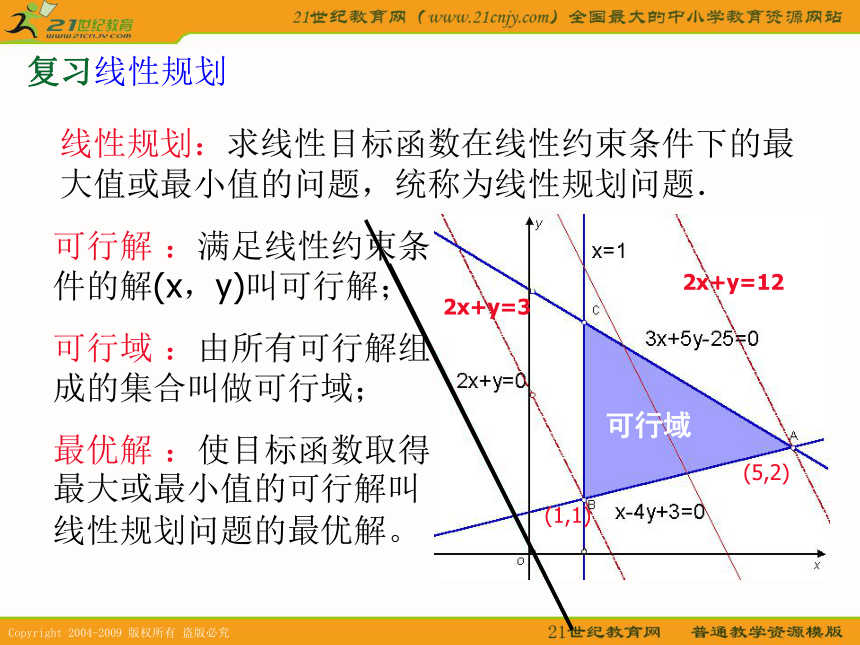
束条件线性规划:求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题. 可行解 :满足线性约束条件的解(x,y)叫可行解; 可行域 :由所有可行解组成的集合叫做可行域; 最优解 :使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。 可行域2x+y=32x+y=12(1,1)(5,2)复习线性规划解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:在可行域内找到最优解所对应的点;
第三步:解方程的最优解,从而求出目标函数的最大值或最小值。探索结论复习线性规划线性规划的实际应用 例1 某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少(精确到吨),能使利润
总额最大?纺纱厂的效益问题线性规划的实际应用解线性规划应用问题的一般步骤:
1、理清题意,列出表格;
2、设好变元,列出线性约束条件(不 等式组)与目标函数;
3、准确作图;
4、根据题设精度计算。 线性规划的实际应用 例1 某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少(精确到吨),能使利润总额最大?纺纱厂的效益问题线性规划的实际应用解:设生产甲、乙两种棉纱分别为x吨、y吨,利润总额为z元,则
Z=600x+900y作出可行域,可知直线Z=600x+900y通过点M时利润最大。解方程组得点M的坐标x=350/3≈117y=200/3≈67答:应生产甲、乙两种棉纱分别为117吨、67吨,能使利润总额达到最大。线性规划的实际应用 例2 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,能使总运费最少?煤矿调运方案问题 线性规划的实际应用 例2 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,能使总运费最少?煤矿调运方案问题 解:设甲煤矿运往东车站x万吨,乙煤矿运往东车站y万吨,则约束条件为:
目标函数为:
z=[x+1.5(200-x)]+[0.8y+1.6(300-y)]
=780-0.5x-0.8y (万元)煤矿调运方案问题答案:当 x=0,y=280时,即甲煤矿运往东车站0吨,西车站200吨;乙煤矿运往东车站280吨,西车站20吨.总运费最少 556万元。线性规划的应用已知:-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围。解法1:由待定系数法: 设 a+3b=m(a+b)+n(a-2 b)
=(m+n)a+(m-2n)b
∴m+n=1,m-2n=3
m=5/3 ,n=-2/3
∴ a+3b=5/3×(a+b)-2/3×(a-2 b)
∵-1≤a+b≤1,1≤a-2 b≤3
∴-11/3≤a+3 b≤1解法2:∵-1≤a+b≤1,1≤a-2 b≤3
∴-2≤2a+2 b≤2,
-3≤2 b-a≤-1
∴-1/3≤a≤5/3
-4/3≤b≤0
∴-13/3≤a+3 b≤5/3想一想线性规划的应用
已知:-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围。解法3 约束条件为:目标函数为:z=a+3b由图形知:-11/3≤z≤1
即 -11/3≤a+3 b≤1线性规划的实际应用小结解线性规划应用问题的一般步骤:
1、理清题意,列出表格;
2、设好变元,列出线性约束条件(不 等式组)与目标函数;
3、准确作图;
4、根据题设精度计算。线性规划的应用作业:P64 习题 7.4 3,4再见
必修53.3.3《线性规划的实际应用》审校:王伟教学目标1.知识目标:
会用线性规划的理论和方法解决一些较简单的实际问题;
2.能力目标:培养学生观察、分析、联想、以及作图的能力,渗透集合、化归、数形结合的数学思想,培养学生自主探究意识,提高学生“建模”和解决实际问题的能力;
3.情感目标:培养学生学习数学的兴趣和“用数学”的意识,激励学生创新,鼓励学生讨论,学会沟通,培养团结协作精神.
教学重点:把实际问题转化成线性规划问题,即建模,并给出解答.
教学难点:
1.建立数学模型.把实际问题转化为线性规划问题;
2.寻找整点最优解的方法.复习二元一次不等式表示的平面区域 在平面直角坐标系中,以二元一次方程x+y-1=0的解为坐标的点的集合{(x,y)|x+y-1=0}是经过点(0,1)和(1,0)的一条直线l,那么以二元一次不等式x+y-1>0的解为坐标的点的集合{(x,y)|x+y-1>0}是
什么图形? 探索结论 结论:二元一次不等式ax+by+c>0在平面直角坐标系中表示直线ax+by+c=0某一侧所有点组成的平面区域。不等式 ax+by+c<0表示的是另一侧的平面区域。x+y-1>0x+y-1<0复习判断二元一次不等式表示哪一侧平面区域的方法x+y-1>0x+y-1<0 由于对在直线ax+by+c=0同
一侧所有点(x,y),把它的坐标
(x,y)代入ax+by+c,所得的实
数的符号都相同,故只需在这条
直线的某一侧取一特殊点(x0,y0)
以ax0+by0+c的正负的情况便可
判断ax+by+c>0表示这一直线
哪一侧的平面区域,特殊地,当
c≠0时常把原点作为此特殊点复习线性规划问题:
设z=2x+y,式中变量满足
下列条件:
求z的最大值与最小值。 目标函数
(线性目标函数)线性约
束条件线性规划:求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题. 可行解 :满足线性约束条件的解(x,y)叫可行解; 可行域 :由所有可行解组成的集合叫做可行域; 最优解 :使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。 可行域2x+y=32x+y=12(1,1)(5,2)复习线性规划解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:在可行域内找到最优解所对应的点;
第三步:解方程的最优解,从而求出目标函数的最大值或最小值。探索结论复习线性规划线性规划的实际应用 例1 某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少(精确到吨),能使利润
总额最大?纺纱厂的效益问题线性规划的实际应用解线性规划应用问题的一般步骤:
1、理清题意,列出表格;
2、设好变元,列出线性约束条件(不 等式组)与目标函数;
3、准确作图;
4、根据题设精度计算。 线性规划的实际应用 例1 某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少(精确到吨),能使利润总额最大?纺纱厂的效益问题线性规划的实际应用解:设生产甲、乙两种棉纱分别为x吨、y吨,利润总额为z元,则
Z=600x+900y作出可行域,可知直线Z=600x+900y通过点M时利润最大。解方程组得点M的坐标x=350/3≈117y=200/3≈67答:应生产甲、乙两种棉纱分别为117吨、67吨,能使利润总额达到最大。线性规划的实际应用 例2 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,能使总运费最少?煤矿调运方案问题 线性规划的实际应用 例2 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,能使总运费最少?煤矿调运方案问题 解:设甲煤矿运往东车站x万吨,乙煤矿运往东车站y万吨,则约束条件为:
目标函数为:
z=[x+1.5(200-x)]+[0.8y+1.6(300-y)]
=780-0.5x-0.8y (万元)煤矿调运方案问题答案:当 x=0,y=280时,即甲煤矿运往东车站0吨,西车站200吨;乙煤矿运往东车站280吨,西车站20吨.总运费最少 556万元。线性规划的应用已知:-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围。解法1:由待定系数法: 设 a+3b=m(a+b)+n(a-2 b)
=(m+n)a+(m-2n)b
∴m+n=1,m-2n=3
m=5/3 ,n=-2/3
∴ a+3b=5/3×(a+b)-2/3×(a-2 b)
∵-1≤a+b≤1,1≤a-2 b≤3
∴-11/3≤a+3 b≤1解法2:∵-1≤a+b≤1,1≤a-2 b≤3
∴-2≤2a+2 b≤2,
-3≤2 b-a≤-1
∴-1/3≤a≤5/3
-4/3≤b≤0
∴-13/3≤a+3 b≤5/3想一想线性规划的应用
已知:-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围。解法3 约束条件为:目标函数为:z=a+3b由图形知:-11/3≤z≤1
即 -11/3≤a+3 b≤1线性规划的实际应用小结解线性规划应用问题的一般步骤:
1、理清题意,列出表格;
2、设好变元,列出线性约束条件(不 等式组)与目标函数;
3、准确作图;
4、根据题设精度计算。线性规划的应用作业:P64 习题 7.4 3,4再见
