2025年深圳市中考备考百师助学培优课程——第14讲45度角解题策略 课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第14讲45度角解题策略 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览





文档简介
(共32张PPT)
45度角问题解决策略
罗湖区中考备考“百师助学”课程第14讲
深圳市东晓中学 洪燕
模块一:45度角问题初探
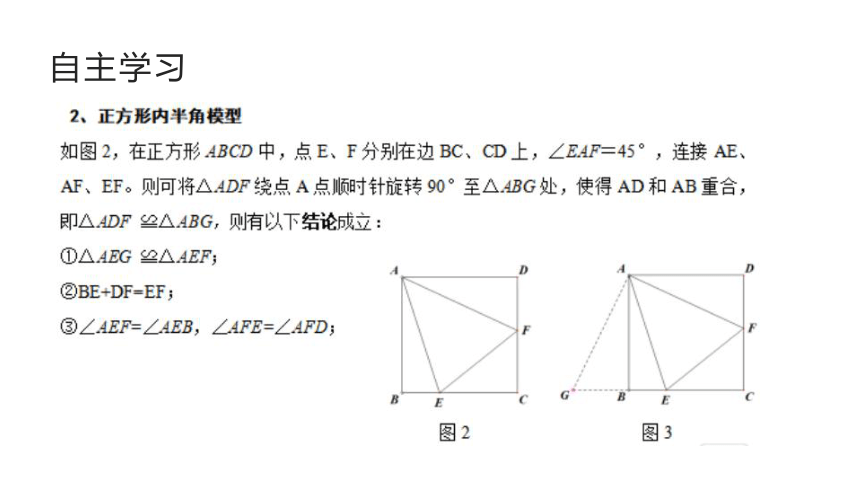
自主学习
自主学习
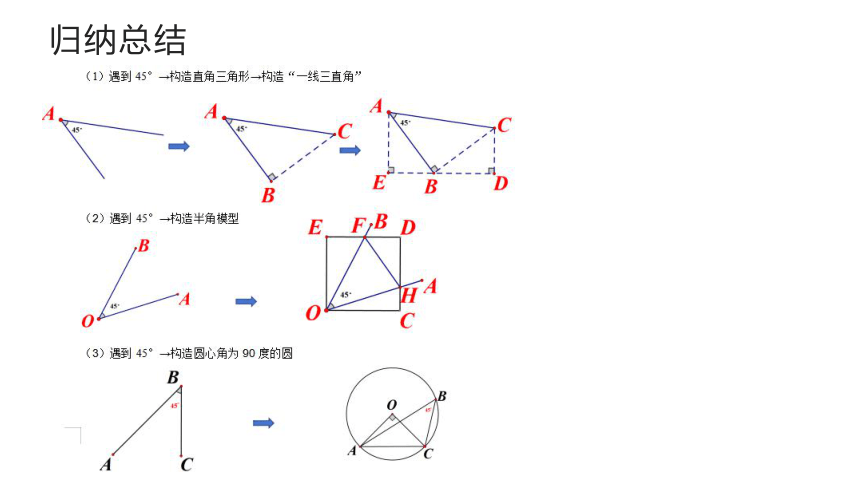
归纳总结
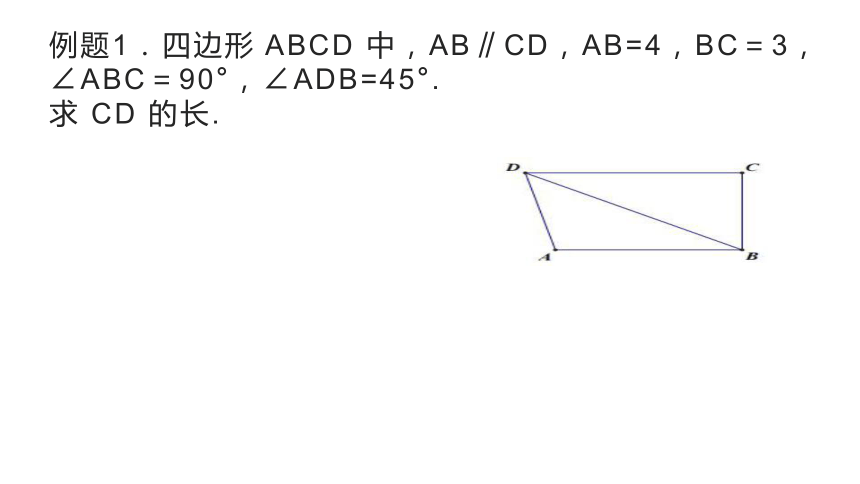
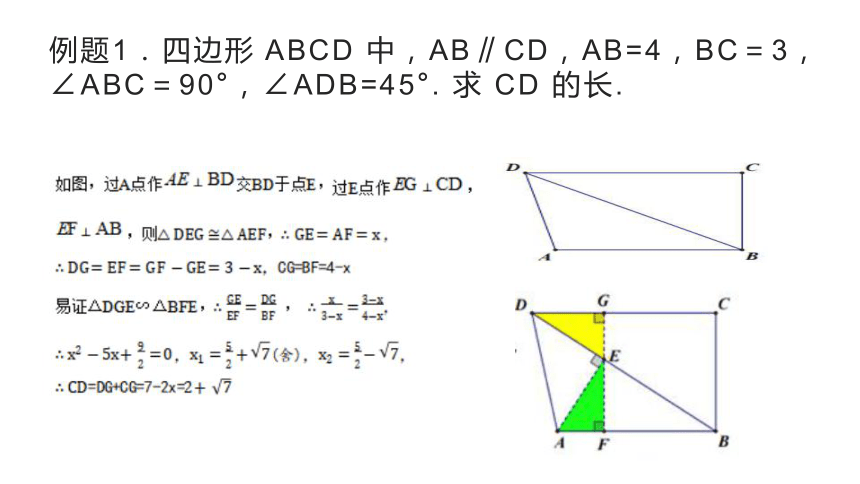
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
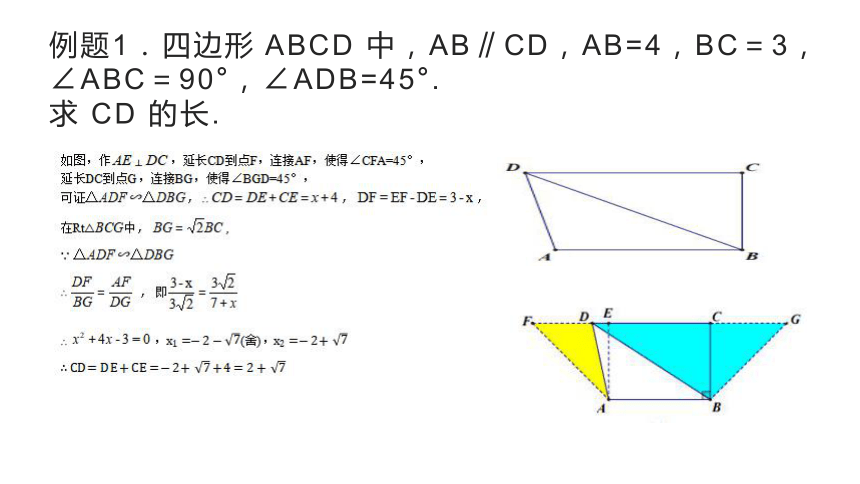
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
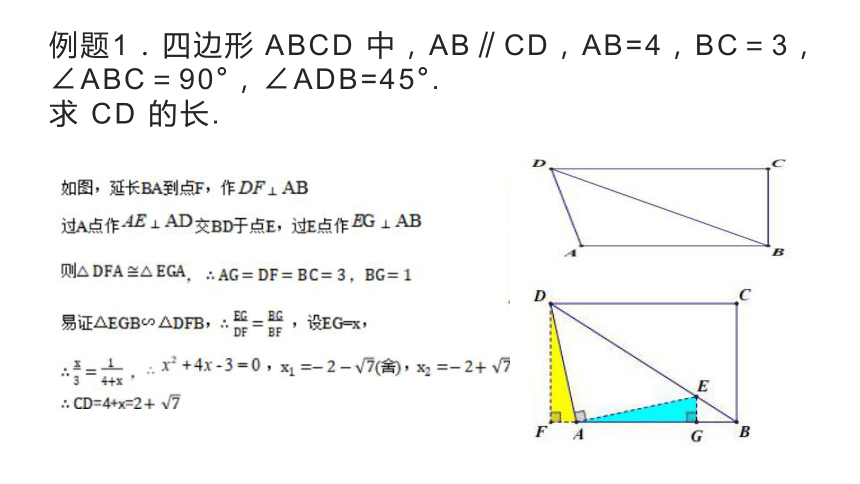
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°. 求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
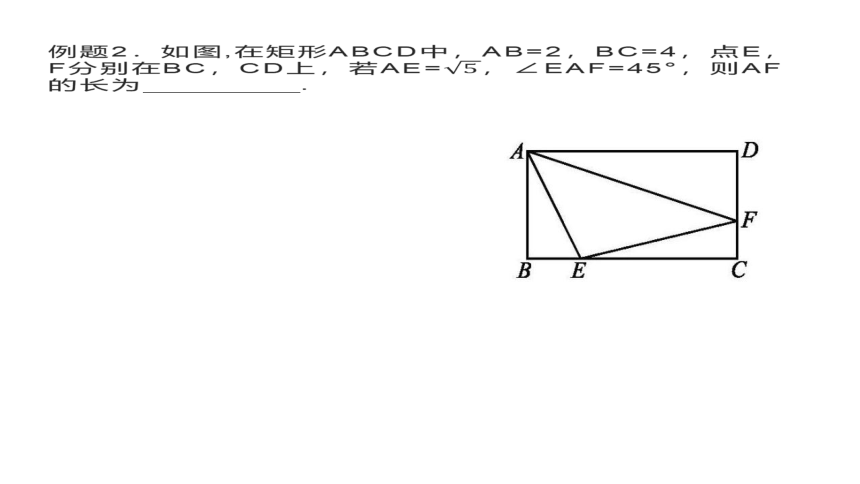
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法1:构造等腰直角三角形,列二元一次方程组求解
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法2:构造等腰直角三角形,利用全等、相似求解
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法3:利用半角模型求解(先构造半角模型,借助△ADF的中位线求出DF,再求AF)
用到一个结论:如图③,已知正方形ABMN,E,G分别是BM,MN上的点,且∠EAG=45°,那么BE+NG=EG.
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法4:构造两个等腰三角形求解
练习
练习
练习
模块二:45度角问题与一次函数、反比例函数结合
模块三: 45度角与二次函数、圆结合
感谢聆听!
45度角问题解决策略
罗湖区中考备考“百师助学”课程第14讲
深圳市东晓中学 洪燕
模块一:45度角问题初探
自主学习
自主学习
归纳总结
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°. 求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法1:构造等腰直角三角形,列二元一次方程组求解
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法2:构造等腰直角三角形,利用全等、相似求解
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法3:利用半角模型求解(先构造半角模型,借助△ADF的中位线求出DF,再求AF)
用到一个结论:如图③,已知正方形ABMN,E,G分别是BM,MN上的点,且∠EAG=45°,那么BE+NG=EG.
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE=,∠EAF=45°,则AF的长为 .
方法4:构造两个等腰三角形求解
练习
练习
练习
模块二:45度角问题与一次函数、反比例函数结合
模块三: 45度角与二次函数、圆结合
感谢聆听!
同课章节目录
