2025年深圳市中考备考百师助学培优课程——第20讲求解圆上动点相关最值问题 课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第20讲求解圆上动点相关最值问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 37.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 09:24:33 | ||
图片预览



文档简介
(共18张PPT)
MATHEMATICS SUBJECT EDUCATION AND TEACHING IN PRIMARY AND SECONDARY SCHOOLS
深圳市红桂中学 范怡静
求解圆上动点相关最值问题
CONTENT
目录
自主探究
01
小组研学
02
进阶训练
03
归纳小结
04
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
模型1
思路分析
OP 、OA长为定值,连接OP 、OA
在△APO中
OA+OP当A、P、O共线时,AP取得最值
方法归纳:连接AO并延长,与圆分别交于点P1、点P2。APmax=OA+OP,APmin=OA-OP
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
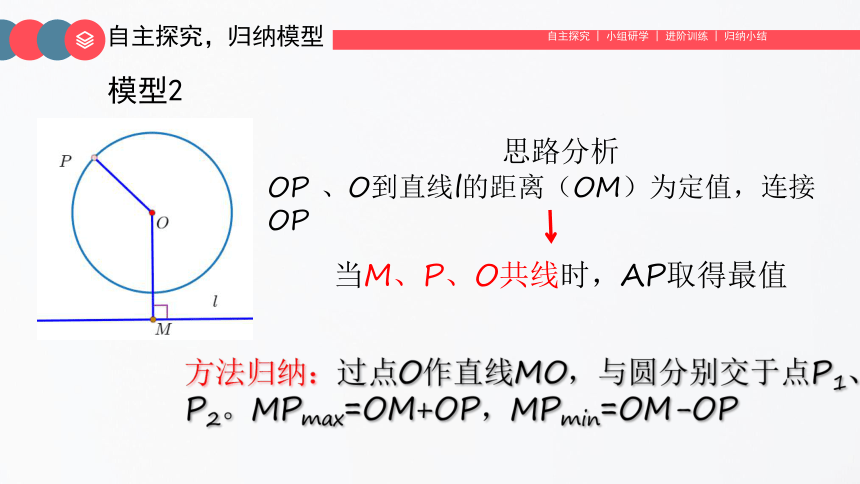
模型2
思路分析
OP 、O到直线l的距离(OM)为定值,连接OP
当M、P、O共线时,AP取得最值
方法归纳:过点O作直线MO,与圆分别交于点P1、P2。MPmax=OM+OP,MPmin=OM-OP
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
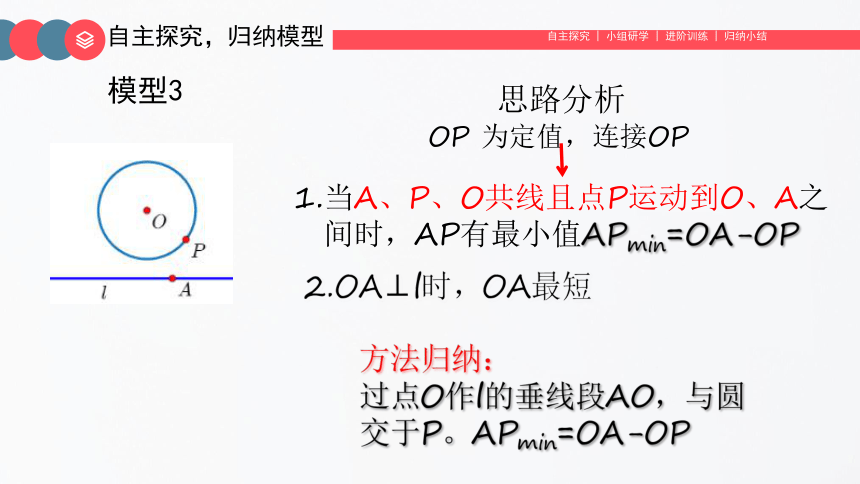
模型3
思路分析
OP 为定值,连接OP
1.当A、P、O共线且点P运动到O、A之间时,AP有最小值APmin=OA-OP
方法归纳:
过点O作l的垂线段AO,与圆交于P。APmin=OA-OP
2.OA⊥l时,OA最短
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
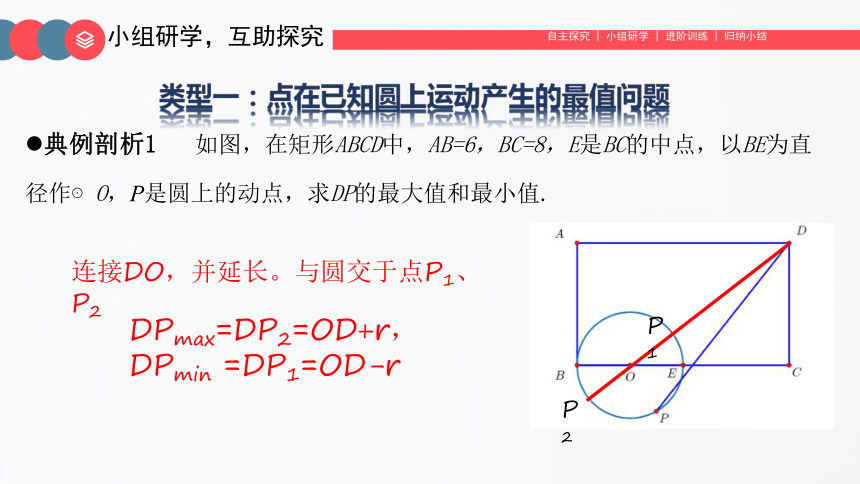
典例剖析1 如图,在矩形ABCD中,AB=6,BC=8,E是BC的中点,以BE为直径作⊙O,P是圆上的动点,求DP的最大值和最小值.
P1
P2
连接DO,并延长。与圆交于点P1、P2
DPmax=DP2=OD+r,
DPmin =DP1=OD-r
类型一:点在已知圆上运动产生的最值问题
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
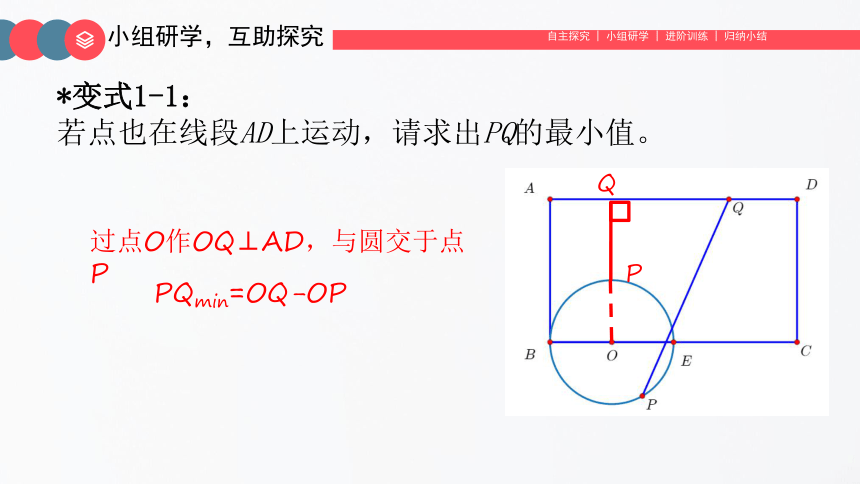
*变式1-1:
若点也在线段AD上运动,请求出PQ的最小值。
Q
P
过点O作OQ⊥AD,与圆交于点P
PQmin=OQ-OP
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
变式1-2:
连接AC、PA、PC,求△APC面积的最小值。并在图中画出取得最小值的情况。
P
F
方法点拨:
S△APC= ×AC×h(点P到线段AC的距离)
面积最小的情况。即求h最小的情况
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
1. 如图,⊙O的半径为10,圆心O到直线l的距离为14,点A是⊙O上一点,过点A的切线与直线l交于点 B,求 AB 的最小值.
AB2=OB2-OA2
当OB最小时,AB也最小
即求OB的最小值
转化
方法点拨:
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型二:点在未知轨迹上运动产生的最值问题
典例剖析2
如图,在矩形ABCD中,AB=6,BC=8,F是AB的中点,E是线段BC上的动点,点B沿着EF折叠得到点B’。求线段DB’的最小值。
方法点拨:
BF=BF'
故点B'位于以F点为圆心,
FB为半径的圆周上
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
2.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,则线段MC的最小值为 .
方法点拨:
AB=AM
故点M位于以A点为圆心,
AB为半径的圆弧上
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
典例剖析3
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=6,P是AB左侧一动点,且AP⊥BP,则线段CP长度的最大值是 .*
方法点拨:
∠ABC=90°,AB=4为定长
故点P位于以AB为直径的圆周上
示意图作法:取AB的中点O,
连接CO 并延长,交圆与点P
O
P
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
3.如图2,Rt△ABC中,AB⊥BC,AB=12,BC=8,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值.
方法点拨:
∵∠ABC=90°
∴∠PBA+∠PBC=90°
∵由题知∠PBC=∠PAB
∴∠PAB+∠PBA=90°
∴∠APB=90°
AB=12为定长
故点P位于以AB为直径的圆周上
方法迁移,进阶训练
自主探究 | 小组研学 | 进阶训练 | 归纳小结
思路点拨:O为AB中点,AB=2OP。AB取得最小值时,即OP取得最小值。
方法迁移,进阶训练
自主探究 | 小组研学 | 进阶训练 | 归纳小结
∵∠AHD=90°,AD为定长
∴点H在以AD为圆心的圆上运动
归纳小结,形成方法
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型一:点在已知圆上运动产生的最值问题
定点与圆上动点距离
定直线与圆上动点距离
直线动点与圆上动点距离
归纳小结,形成方法
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型二:点在未知轨迹上运动产生的最值问题
利用条件、借助性质还原轨迹,“无中生有”
终极宝典
动点问题终极宝典
转化对象,以静制动
MATHEMATICS SUBJECT EDUCATION AND TEACHING IN PRIMARY AND SECONDARY SCHOOLS
深圳市红桂中学 范怡静
求解圆上动点相关最值问题
CONTENT
目录
自主探究
01
小组研学
02
进阶训练
03
归纳小结
04
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
模型1
思路分析
OP 、OA长为定值,连接OP 、OA
在△APO中
OA+OP
方法归纳:连接AO并延长,与圆分别交于点P1、点P2。APmax=OA+OP,APmin=OA-OP
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
模型2
思路分析
OP 、O到直线l的距离(OM)为定值,连接OP
当M、P、O共线时,AP取得最值
方法归纳:过点O作直线MO,与圆分别交于点P1、P2。MPmax=OM+OP,MPmin=OM-OP
自主探究,归纳模型
自主探究 | 小组研学 | 进阶训练 | 归纳小结
模型3
思路分析
OP 为定值,连接OP
1.当A、P、O共线且点P运动到O、A之间时,AP有最小值APmin=OA-OP
方法归纳:
过点O作l的垂线段AO,与圆交于P。APmin=OA-OP
2.OA⊥l时,OA最短
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
典例剖析1 如图,在矩形ABCD中,AB=6,BC=8,E是BC的中点,以BE为直径作⊙O,P是圆上的动点,求DP的最大值和最小值.
P1
P2
连接DO,并延长。与圆交于点P1、P2
DPmax=DP2=OD+r,
DPmin =DP1=OD-r
类型一:点在已知圆上运动产生的最值问题
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
*变式1-1:
若点也在线段AD上运动,请求出PQ的最小值。
Q
P
过点O作OQ⊥AD,与圆交于点P
PQmin=OQ-OP
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
变式1-2:
连接AC、PA、PC,求△APC面积的最小值。并在图中画出取得最小值的情况。
P
F
方法点拨:
S△APC= ×AC×h(点P到线段AC的距离)
面积最小的情况。即求h最小的情况
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
1. 如图,⊙O的半径为10,圆心O到直线l的距离为14,点A是⊙O上一点,过点A的切线与直线l交于点 B,求 AB 的最小值.
AB2=OB2-OA2
当OB最小时,AB也最小
即求OB的最小值
转化
方法点拨:
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型二:点在未知轨迹上运动产生的最值问题
典例剖析2
如图,在矩形ABCD中,AB=6,BC=8,F是AB的中点,E是线段BC上的动点,点B沿着EF折叠得到点B’。求线段DB’的最小值。
方法点拨:
BF=BF'
故点B'位于以F点为圆心,
FB为半径的圆周上
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
2.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,则线段MC的最小值为 .
方法点拨:
AB=AM
故点M位于以A点为圆心,
AB为半径的圆弧上
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
典例剖析3
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=6,P是AB左侧一动点,且AP⊥BP,则线段CP长度的最大值是 .*
方法点拨:
∠ABC=90°,AB=4为定长
故点P位于以AB为直径的圆周上
示意图作法:取AB的中点O,
连接CO 并延长,交圆与点P
O
P
小组研学,互助探究
自主探究 | 小组研学 | 进阶训练 | 归纳小结
针对训练
3.如图2,Rt△ABC中,AB⊥BC,AB=12,BC=8,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值.
方法点拨:
∵∠ABC=90°
∴∠PBA+∠PBC=90°
∵由题知∠PBC=∠PAB
∴∠PAB+∠PBA=90°
∴∠APB=90°
AB=12为定长
故点P位于以AB为直径的圆周上
方法迁移,进阶训练
自主探究 | 小组研学 | 进阶训练 | 归纳小结
思路点拨:O为AB中点,AB=2OP。AB取得最小值时,即OP取得最小值。
方法迁移,进阶训练
自主探究 | 小组研学 | 进阶训练 | 归纳小结
∵∠AHD=90°,AD为定长
∴点H在以AD为圆心的圆上运动
归纳小结,形成方法
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型一:点在已知圆上运动产生的最值问题
定点与圆上动点距离
定直线与圆上动点距离
直线动点与圆上动点距离
归纳小结,形成方法
自主探究 | 小组研学 | 进阶训练 | 归纳小结
类型二:点在未知轨迹上运动产生的最值问题
利用条件、借助性质还原轨迹,“无中生有”
终极宝典
动点问题终极宝典
转化对象,以静制动
同课章节目录
