2025年罗湖区中考备考百师助学课程之第四讲《对角互补模型在中考数学中的应用》 教学设计
文档属性
| 名称 | 2025年罗湖区中考备考百师助学课程之第四讲《对角互补模型在中考数学中的应用》 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 09:30:48 | ||
图片预览




文档简介
《对角互补模型在中考数学中的应用教学设计》-----徐国雄
一、核心素养目标
1. 逻辑推理
学生能通过分析条件与结论的逻辑关联,识别对角互补模型中的隐藏关系(如全等三角形、相似比、圆周角定理),提升演绎推理能力。
通过“构造线段关系”或“转化角量”解决复杂几何问题,培养逻辑链条的严谨性与系统性。
2. 空间观念
借助几何画板动态演示图形旋转、点运动等变化过程,帮助学生建立二维与三维空间模型认知,强化对图形稳定属性的直观理解。
3. 数学建模
能根据题设特征判断适用模型(全等型/相似型/共圆型),并通过辅助线设计与代数化表达实现问题的数学化处理。
4. 问题解决与运算优化
灵活切换模型方法解决多步骤问题(如比例线段计算、参数取值范围问题),养成分类讨论意识。
教学重点与难点
教学重点
对角互补模型的核心条件识别。
教学难点
直角与45°、60°及一般角度下辅助线构造逻辑。
三、教学过程
模块一:全等型
模块一:典例精讲
例1 如图:已知OC平分∠AOB,,
的两边分别与OA交于点D,OB交于点E,求证:
(1)CD=CE;
(2)OD+OE=OC;
(3)
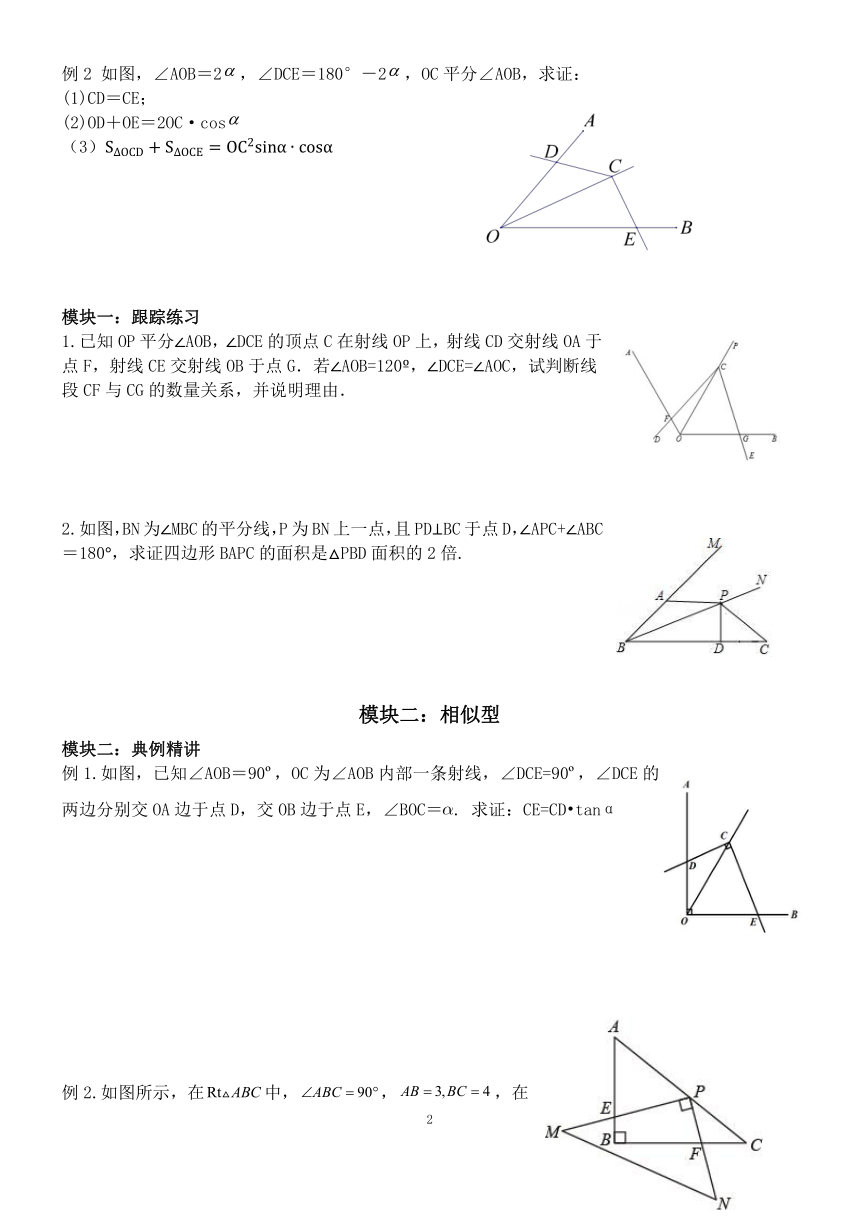
例2 如图,∠AOB=2,∠DCE=180°-2,OC平分∠AOB,求证:
(1)CD=CE;
(2)OD+OE=2OC·cos
(3)
模块一:跟踪练习
1.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.若∠AOB=120 ,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
2.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,求证四边形BAPC的面积是△PBD面积的2倍.
模块二:相似型
模块二:典例精讲
例1.如图,已知∠AOB=90 ,OC为∠AOB内部一条射线,∠DCE=90 ,∠DCE的两边分别交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan
例2.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,求的值.
模块二:跟踪练习
1.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当时,的值为 ;当时,为 .(用含n的式子表示)
2.如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为线段AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
模块三:四点共圆--综合题
模块三:典例精讲
例1 如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆.
例2 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=( )
A. B. C. D.
模块三:跟踪练习
如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
如图,在△ABC中,∠C=45°,∠B=60°,BC为+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为 .
答案解析
模块一:典例精讲
例1 如图:已知OC平分∠AOB,,
的两边分别与OA交于点D,OB交于点E,求证:
(1)CD=CE;
(2)OD+OE=OC;
(3)
答案解析:
如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N.
由角平分线的性质可得CM=CN,∠MCN=90°.
所以∠MCD=∠NCE,
从而△MCD≌△NCE(ASA),
故CD=CE.
易证四边形MONC为正方形.
所以OD+OE=OD+ON+NE=2ON=OC.
所以.
例2 如图,∠AOB=2,∠DCE=180°-2,OC平分∠AOB,求证::
CD=CE;
OD+OE=2OC·cos
(3)
答案解析:
如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N
易证△MCD≌△NCE(ASA)
∴CD=CE,OD+OE=2ON=2OC·cos
∴
模块一:跟踪练习
1.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.若∠AOB=120 ,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
答案解析:
CF=CG.理由如下:如图,
过点C作CM⊥OA,CN⊥OB,∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120 ,
∴CM=CN(角平分线上的点到角两边的距离相等),
∴∠AOC=∠BOC=60 (角平分线的性质),
∵∠DCE=∠AOC,∴∠AOC=∠BOC=∠DCE=60 ,
∴∠MCO=90 -60 =30 ,∠NCO=90 -60 =30 ,
∴∠MCN=30 +30 =60 ,∴∠MCN=∠DCE,
∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,∴∠MCF=∠NCG,
在△MCF和△NCG中,
∴△MCF≌△NCG(ASA),∴CF=CG(全等三角形对应边相等);
如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,求证四边形BAPC的面积是△PBD面积的2倍.
答案解析:
过点P作PK⊥AB,垂足为点K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,∴PK=PD,
在Rt△BPK和Rt△BPD中,,
∴Rt△BPK≌Rt△BPD(HL),∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,
∴∠KPD=∠APC,∴∠APK=∠CPD,
在△PAK和△PCD中,,
∴△PAK≌△PCD(ASA),∴AK=CD,PA=PC,
∴BK﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.
模块二:相似型
模块二:典例精讲
例1.如图,已知∠AOB=90 ,OC为∠AOB内部一条射线,∠DCE=90 ,∠DCE的两边分别交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan
答案解析:
∵CF⊥OA,CG⊥OB,垂足分别为F,G;
∴∠EGC=∠DFC=90°,
∵∠AOB=90°,
∴四边形OGCF为矩形,
∴∠GCF=90°,CF=OG,
∴∠FCD+∠DCG=90°,
∵∠DCE=90°,
∴∠GCE+∠DCG=90°,
∴∠GCE=∠FCD,
∴△ECG∽△DCF,
∴,
∵CF=OG,
∴,
∵在Rt△COG中,,
∴CE=CD·
例2.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,求的值.
答案解析:
∵在中,,,
∴AC= ,
过P作PH⊥BC于H,PQ⊥AB于Q,则∠PQB=∠PHB=∠B=90°,
∴四边形PQBH是矩形,
∴PH=BQ,∠QPH=90°=∠MPN,PQ∥BC,
∴∠EPH+∠QPE=∠EPH+∠HPF=90°,
∴∠QPE=∠HPF,
∴△PQE∽△PHF,
∴,
又PE=2PF,
∴PQ=2PH=2BQ,
∵PQ∥BC,
∴△AQP∽△ABC,
∴,
设BQ=x,则AQ=3﹣x,PQ=2x,
∴,
解得:,AP=3
模块二:跟踪练习
1.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当时,的值为 ;当时,为 .(用含n的式子表示)
答案解析:作OD⊥AC于D,OE⊥BC于E,如图,
∵∠ACB=90°,
∴OD∥BC,OE∥AC,
∴△AOD∽△ABC,△BOE∽△BAC,
∴=,=,
∵,
∴=,=,
∴=,=,
∴=,
在Rt△ABC中,tanB=tan30°==,即=,
∴=,
∵∠POQ=90°,
而∠DOE=90°,
∴∠DOP=∠QOE,
∴Rt△DOP∽Rt△EOQ,
∴==,
当n=2时,即时,=.
故答案为,.
2.如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为线段AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
答案解析:
(1)∵∠A=90°,AB=12,AC=16,
∴根据勾股定理得到,BC==20,
∴CD=BC=10,
∵DE⊥BC,
∴∠A=∠CDE=90°,∠C=∠C,
∴△CDE∽△CAB,
∴DE:AB=CE:CB=CD:CA,
即DE:12=CE:20=10:16,
∴DE=,CE=;
(2)∵△CDE∽△CAB,
∴∠B=∠DEC,
∵∠PDQ=90°,
∴∠QDC+∠PDB=90°,
∵∠QDC+∠EDQ=90°,
∴∠EDQ=∠PDB,
∴△PBD∽△QED,
∴=,即=,
∴EQ=,
∴CQ=CE﹣EQ=﹣=11;
(3)∵线段PQ与线段DE的交点为点F,
∴点P在边AB上,
∵△BPD∽△EQD,
∴====,
若设BP=x,则EQ=x,CQ=﹣x,
∵=,==,
∴∠QPD=∠C,
∵∠PDE=∠CDQ,
∴△PDF∽△CDQ,
∵△PDF为等腰三角形,
∴△CDQ为等腰三角形,
①当CQ=CD时,可得:﹣x=10,
解得:x=;
②当QC=QD时,过点Q作QM⊥CB于M,如图3所示,
∴CM=CD=5,
∵cos∠C====,
∴CQ=,
∴﹣x=,
解得:x=;
∴综上所述,BP=或.
模块三:四点共圆--综合题
模块三:典例精讲
例1 如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆.
答案解析:
过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,
若C在圆外,如图1,设BC交圆O于C′,
根据圆内接四边形的性质得∠A+∠DC′B=180°,
∵∠A+∠C=180°,
∴∠DC′B=∠C,
这与三角形外角定理矛盾,故C不可能在圆外;
类似地(如图2)点C不可能在圆内;
∴C在圆O上,也即A,B,C,D四点共圆.
例2 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=( )
A. B. C. D.
答案解析:
如图,连接BF,取BF的中点O,连接OE,OC.
∵四边形ABCD是矩形,EF⊥BE,
∴四边形EFCB对角互补,
∴B,C,F,E四点共圆,
∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5,
∵OB=OF,
∴OE=OB=OF=OC,
∴B,C,F,E四点在以O为圆心的圆上,
∴∠EBF=∠ECF,
∴tan∠EBF=tan∠ACD,
∴==,
模块三:跟踪练习
1.如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
答案解析:
如图取BE的中点K.连接AK、OK.
∵四边形ABCD是矩形,
∴∠BAE=90°,
∵EO⊥BD,
∴∠BOE=90°,
∴四边形ABOE对角互补,
∴A、B、O、E四点共圆,
∵BK=KE,
∴KA=KB=KO=KE,
∴∠ABE=∠AOE=20°
2.如图,在△ABC中,∠C=45°,∠B=60°,BC为+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为 .
答案解析:
连接CP,如图:
∵PD⊥BC于点D,PE⊥AC于点E,
∴∠PDC=∠PEC=90°,
∴∠PDC+∠PEC=180°,
∴C、D、P、E四点共圆,圆心为O,且直径为CP,
∵BC=+1,∠ACB=45°是定值,
∴直径CP最小时,∠DCE所对的弦DE最小,
即CP⊥AB时,DE最小,
连接OD、OE,
∵∠B=60°,CP⊥AB,BC=+1,
∴∠BCP=30°,
∴BP=BC=,CP=BP=,
∴OD=OE=CP=,
又∵∠ACB=45°,
∴∠DOE=2∠ACB=90°,
∴△ODE是等腰直角三角形,
∴DE=OD=;
即DE的最小值为;
故答案为:.
教学反思
1. 模型融合教学适配性
实际课堂中,学生常混淆共圆模型与全等构造的适用边界,后续需加强典型案例对比分析。
2. 可视化工具的应用效能
几何画板的动态展示有效提升认知参与度,但需控制演示节奏,预留记录与复现机会,确保知识内化而非替代思考。
3. 分层教学策略优化
发现部分学生对相似比的字母式转化存在理解障碍,后续拟采用表格对比法梳理常见比例关系模板(如射影定理类比),降低陌生感。
(北京)股份有限公司(北京)股份有限公司
(北京)股份有限公司(北京)股份有限公司
2
一、核心素养目标
1. 逻辑推理
学生能通过分析条件与结论的逻辑关联,识别对角互补模型中的隐藏关系(如全等三角形、相似比、圆周角定理),提升演绎推理能力。
通过“构造线段关系”或“转化角量”解决复杂几何问题,培养逻辑链条的严谨性与系统性。
2. 空间观念
借助几何画板动态演示图形旋转、点运动等变化过程,帮助学生建立二维与三维空间模型认知,强化对图形稳定属性的直观理解。
3. 数学建模
能根据题设特征判断适用模型(全等型/相似型/共圆型),并通过辅助线设计与代数化表达实现问题的数学化处理。
4. 问题解决与运算优化
灵活切换模型方法解决多步骤问题(如比例线段计算、参数取值范围问题),养成分类讨论意识。
教学重点与难点
教学重点
对角互补模型的核心条件识别。
教学难点
直角与45°、60°及一般角度下辅助线构造逻辑。
三、教学过程
模块一:全等型
模块一:典例精讲
例1 如图:已知OC平分∠AOB,,
的两边分别与OA交于点D,OB交于点E,求证:
(1)CD=CE;
(2)OD+OE=OC;
(3)
例2 如图,∠AOB=2,∠DCE=180°-2,OC平分∠AOB,求证:
(1)CD=CE;
(2)OD+OE=2OC·cos
(3)
模块一:跟踪练习
1.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.若∠AOB=120 ,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
2.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,求证四边形BAPC的面积是△PBD面积的2倍.
模块二:相似型
模块二:典例精讲
例1.如图,已知∠AOB=90 ,OC为∠AOB内部一条射线,∠DCE=90 ,∠DCE的两边分别交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan
例2.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,求的值.
模块二:跟踪练习
1.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当时,的值为 ;当时,为 .(用含n的式子表示)
2.如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为线段AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
模块三:四点共圆--综合题
模块三:典例精讲
例1 如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆.
例2 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=( )
A. B. C. D.
模块三:跟踪练习
如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
如图,在△ABC中,∠C=45°,∠B=60°,BC为+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为 .
答案解析
模块一:典例精讲
例1 如图:已知OC平分∠AOB,,
的两边分别与OA交于点D,OB交于点E,求证:
(1)CD=CE;
(2)OD+OE=OC;
(3)
答案解析:
如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N.
由角平分线的性质可得CM=CN,∠MCN=90°.
所以∠MCD=∠NCE,
从而△MCD≌△NCE(ASA),
故CD=CE.
易证四边形MONC为正方形.
所以OD+OE=OD+ON+NE=2ON=OC.
所以.
例2 如图,∠AOB=2,∠DCE=180°-2,OC平分∠AOB,求证::
CD=CE;
OD+OE=2OC·cos
(3)
答案解析:
如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N
易证△MCD≌△NCE(ASA)
∴CD=CE,OD+OE=2ON=2OC·cos
∴
模块一:跟踪练习
1.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.若∠AOB=120 ,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
答案解析:
CF=CG.理由如下:如图,
过点C作CM⊥OA,CN⊥OB,∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120 ,
∴CM=CN(角平分线上的点到角两边的距离相等),
∴∠AOC=∠BOC=60 (角平分线的性质),
∵∠DCE=∠AOC,∴∠AOC=∠BOC=∠DCE=60 ,
∴∠MCO=90 -60 =30 ,∠NCO=90 -60 =30 ,
∴∠MCN=30 +30 =60 ,∴∠MCN=∠DCE,
∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,∴∠MCF=∠NCG,
在△MCF和△NCG中,
∴△MCF≌△NCG(ASA),∴CF=CG(全等三角形对应边相等);
如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,求证四边形BAPC的面积是△PBD面积的2倍.
答案解析:
过点P作PK⊥AB,垂足为点K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,∴PK=PD,
在Rt△BPK和Rt△BPD中,,
∴Rt△BPK≌Rt△BPD(HL),∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,
∴∠KPD=∠APC,∴∠APK=∠CPD,
在△PAK和△PCD中,,
∴△PAK≌△PCD(ASA),∴AK=CD,PA=PC,
∴BK﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.
模块二:相似型
模块二:典例精讲
例1.如图,已知∠AOB=90 ,OC为∠AOB内部一条射线,∠DCE=90 ,∠DCE的两边分别交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan
答案解析:
∵CF⊥OA,CG⊥OB,垂足分别为F,G;
∴∠EGC=∠DFC=90°,
∵∠AOB=90°,
∴四边形OGCF为矩形,
∴∠GCF=90°,CF=OG,
∴∠FCD+∠DCG=90°,
∵∠DCE=90°,
∴∠GCE+∠DCG=90°,
∴∠GCE=∠FCD,
∴△ECG∽△DCF,
∴,
∵CF=OG,
∴,
∵在Rt△COG中,,
∴CE=CD·
例2.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,求的值.
答案解析:
∵在中,,,
∴AC= ,
过P作PH⊥BC于H,PQ⊥AB于Q,则∠PQB=∠PHB=∠B=90°,
∴四边形PQBH是矩形,
∴PH=BQ,∠QPH=90°=∠MPN,PQ∥BC,
∴∠EPH+∠QPE=∠EPH+∠HPF=90°,
∴∠QPE=∠HPF,
∴△PQE∽△PHF,
∴,
又PE=2PF,
∴PQ=2PH=2BQ,
∵PQ∥BC,
∴△AQP∽△ABC,
∴,
设BQ=x,则AQ=3﹣x,PQ=2x,
∴,
解得:,AP=3
模块二:跟踪练习
1.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当时,的值为 ;当时,为 .(用含n的式子表示)
答案解析:作OD⊥AC于D,OE⊥BC于E,如图,
∵∠ACB=90°,
∴OD∥BC,OE∥AC,
∴△AOD∽△ABC,△BOE∽△BAC,
∴=,=,
∵,
∴=,=,
∴=,=,
∴=,
在Rt△ABC中,tanB=tan30°==,即=,
∴=,
∵∠POQ=90°,
而∠DOE=90°,
∴∠DOP=∠QOE,
∴Rt△DOP∽Rt△EOQ,
∴==,
当n=2时,即时,=.
故答案为,.
2.如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为线段AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
答案解析:
(1)∵∠A=90°,AB=12,AC=16,
∴根据勾股定理得到,BC==20,
∴CD=BC=10,
∵DE⊥BC,
∴∠A=∠CDE=90°,∠C=∠C,
∴△CDE∽△CAB,
∴DE:AB=CE:CB=CD:CA,
即DE:12=CE:20=10:16,
∴DE=,CE=;
(2)∵△CDE∽△CAB,
∴∠B=∠DEC,
∵∠PDQ=90°,
∴∠QDC+∠PDB=90°,
∵∠QDC+∠EDQ=90°,
∴∠EDQ=∠PDB,
∴△PBD∽△QED,
∴=,即=,
∴EQ=,
∴CQ=CE﹣EQ=﹣=11;
(3)∵线段PQ与线段DE的交点为点F,
∴点P在边AB上,
∵△BPD∽△EQD,
∴====,
若设BP=x,则EQ=x,CQ=﹣x,
∵=,==,
∴∠QPD=∠C,
∵∠PDE=∠CDQ,
∴△PDF∽△CDQ,
∵△PDF为等腰三角形,
∴△CDQ为等腰三角形,
①当CQ=CD时,可得:﹣x=10,
解得:x=;
②当QC=QD时,过点Q作QM⊥CB于M,如图3所示,
∴CM=CD=5,
∵cos∠C====,
∴CQ=,
∴﹣x=,
解得:x=;
∴综上所述,BP=或.
模块三:四点共圆--综合题
模块三:典例精讲
例1 如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆.
答案解析:
过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,
若C在圆外,如图1,设BC交圆O于C′,
根据圆内接四边形的性质得∠A+∠DC′B=180°,
∵∠A+∠C=180°,
∴∠DC′B=∠C,
这与三角形外角定理矛盾,故C不可能在圆外;
类似地(如图2)点C不可能在圆内;
∴C在圆O上,也即A,B,C,D四点共圆.
例2 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=( )
A. B. C. D.
答案解析:
如图,连接BF,取BF的中点O,连接OE,OC.
∵四边形ABCD是矩形,EF⊥BE,
∴四边形EFCB对角互补,
∴B,C,F,E四点共圆,
∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5,
∵OB=OF,
∴OE=OB=OF=OC,
∴B,C,F,E四点在以O为圆心的圆上,
∴∠EBF=∠ECF,
∴tan∠EBF=tan∠ACD,
∴==,
模块三:跟踪练习
1.如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
答案解析:
如图取BE的中点K.连接AK、OK.
∵四边形ABCD是矩形,
∴∠BAE=90°,
∵EO⊥BD,
∴∠BOE=90°,
∴四边形ABOE对角互补,
∴A、B、O、E四点共圆,
∵BK=KE,
∴KA=KB=KO=KE,
∴∠ABE=∠AOE=20°
2.如图,在△ABC中,∠C=45°,∠B=60°,BC为+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为 .
答案解析:
连接CP,如图:
∵PD⊥BC于点D,PE⊥AC于点E,
∴∠PDC=∠PEC=90°,
∴∠PDC+∠PEC=180°,
∴C、D、P、E四点共圆,圆心为O,且直径为CP,
∵BC=+1,∠ACB=45°是定值,
∴直径CP最小时,∠DCE所对的弦DE最小,
即CP⊥AB时,DE最小,
连接OD、OE,
∵∠B=60°,CP⊥AB,BC=+1,
∴∠BCP=30°,
∴BP=BC=,CP=BP=,
∴OD=OE=CP=,
又∵∠ACB=45°,
∴∠DOE=2∠ACB=90°,
∴△ODE是等腰直角三角形,
∴DE=OD=;
即DE的最小值为;
故答案为:.
教学反思
1. 模型融合教学适配性
实际课堂中,学生常混淆共圆模型与全等构造的适用边界,后续需加强典型案例对比分析。
2. 可视化工具的应用效能
几何画板的动态展示有效提升认知参与度,但需控制演示节奏,预留记录与复现机会,确保知识内化而非替代思考。
3. 分层教学策略优化
发现部分学生对相似比的字母式转化存在理解障碍,后续拟采用表格对比法梳理常见比例关系模板(如射影定理类比),降低陌生感。
(北京)股份有限公司(北京)股份有限公司
(北京)股份有限公司(北京)股份有限公司
2
同课章节目录
