1.3不共线三点确定二次函数的表达式 课件 (1)(25PPT)
文档属性
| 名称 | 1.3不共线三点确定二次函数的表达式 课件 (1)(25PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 00:00:00 | ||
图片预览








文档简介
课件25张PPT。
1.3不共线三点确定
二次函数的表达式湘教版九年级下册学习目标1.掌握二次函数解析式的三种形式;
2.学会用待定系数法求经过不共线三点确定的二次函数解析式;
3.体会数形结合的思想方法;
4.感受数学的无穷魅力,体验合作交流探索数学的乐趣.1、一次函数图象经过(2,3)和(-1,-3)
两点,求这个一次函数的解析式? 复习与思考右图为一个二次函数的图像,根据图像提供的信息,
请你写出这个二次函数的相关结论,同学们比一比,
看谁写得多.2、动脑筋,想一想(1)二次函数图像开口向上(2)顶点坐标是(1,-1),
对称轴是x=1(3)当x=1时,函数有最小值-1(4)当x>1时,y随x的增大而增大,
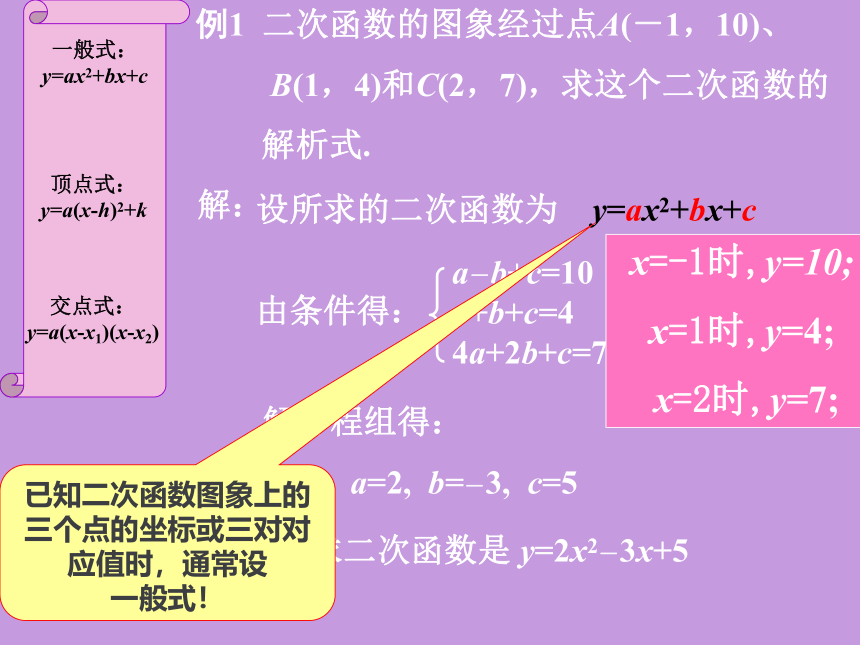
当x<1时,y随x的增大而减小(5)函数图像与x轴交于点(0,0)、(2,0)(6)函数图像经过第一、二、四象限你还能求得这个二次函数其它哪些结论?3、二次函数的解析式有哪些形式?1、一般式2、顶点式3、交点式 和 是抛物线与x轴的两个交点坐标! 顶点坐标是(h,k)例1 二次函数的图象经过点A(-1,10)、
B(1,4)和C(2,7),求这个二次函数的
解析式.一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=ax2+bx+c由条件得:a-b+c=10
a+b+c=4
4a+2b+c=7解方程组得:∴所求二次函数是a=2, b=-3, c=5y=2x2-3x+5已知二次函数图象上的三个点的坐标或三对对应值时,通常设
一般式!x=-1时,y=10;
x=1时,y=4;
x=2时,y=7;解: ∴存在二次函数为y=x2-2x-3例2、是否有一个二次函数,它的图象过
三点(0,-3), (4,5),(-1, 0)?∵二次函数的图象过点(0,-3)(4,5)(-1, 0)∴设有二次函数为 y=ax2+bx+c符合题意例2表明:若给定不共线三点的坐标,
且它们的横坐标两两不相等,
则经过这三点可以确定一个二次函数。
可以证明:二次函数的图像上任意三
个不同的点都不在一条直线上。练习1:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.解:设存在二次函数为y=ax2+bx+c由已知,这个函数的图象过(0,1),可以得到c=1又由于其图象过(2,4)、(3,10)两点,可以得到解这个方程组,得:所以,存在二次函数的关系式是练习2、是否有一个二次函数,它的图象过
三点(0,1), (2,4),(3, 10)?例3 已知抛物线的顶点为(-1,-3),与y
轴交点为(0,-5),求抛物线的解析式?一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=a(x+1)2-3∵点( 0, -5 )在抛物线上,∴a-3=-5, 得a=-2∴所求的抛物线解析式为
y=-2(x+1)2-3即 y=-2x2-4x-5
已知二次函数图象的顶点的坐标时,通常设顶点式!练习3:
已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?∵点( 0,-3)在抛物线上∴a-4=-3, ∴所求的抛物线解析式为 y=(x-1)2-4 a=1x=1,y最值=-4已知条件中的当x=1时有最值-4
也就是抛物线的顶点坐标为(1,-4),
所以设为顶点式较方便例4 已知抛物线与x轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=a(x+1)(x-1)∵点M( 0,1 )在抛物线上,∴a(0+1)(0-1)=1得 a=-1∴所求的抛物线解析式为
y=-(x+1)(x-1)即 y=-x2+1
已知二次函数图象与x轴的两个交点的横坐标时,通常设
交点式!练习4:已知抛物线与x轴两交点横坐标为1,3,且图像过(0,-3),求出对应的二次函数解析式。解:设所求的二次函数为y=a(x-1)(x-3),已知抛物线与x轴的交点
或交点横坐标时,通常
设为交点式(两根式)∵过点(0,-3),∴ a(0-1)(0-3)=-3,∴a=-1∴ y=-(x-1)(x-3),即y=-x2+4x-3例5、已知二次函数 的图像如图所示,
求其解析式。解法一: 一般式∴ 应用举例设解析式为 即:解得例5、已知二次函数 的图像如图所示,
求其解析式。解法二:顶点式∵顶点C(1,4)又∵A(-1,0)在抛物线上, ∴ a = -1 应用举例设解析式为解法三:交点式∵抛物线与x 轴的两个交点坐标
为 A (-1,0)、B(3,0)∴设解析式为y = a (x+1) (x- 3)又 C(1,4)在抛物线上∴ 4 = a (1+1) (1-3)∴ a = -1 ∴ y = - ( x+1) (x-3)例5、已知二次函数 的图像如图所示,
求其解析式。 应用举例∵对称轴 x=1.∴A(-1,0)关于 x=1的对称点B(3,0)。 你能用几种方法求出右图对应的二次函数解析式只要求列式1、观察下列条件,说出求解析式的方法⑴抛物线经过(0,-5)(5,0)两点,对称轴是直线 x = 2⑵二次函数图象经过(0,4),且当 x = 1时,函数值为3;当 x = -1时,函数值为4⑶抛物线的顶点坐标为(2,4),且经过原点⑷抛物线经过点(0,-4),且当 x = 2时,函数图象最高点的纵坐标是4当堂测试你该怎样设?已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。2、你能用几种方法求解解法一: 一般式解得已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。 解:设此抛物线的解析式为:解法二:顶点式∵过点 N(1,0)∴0 = 4a – 2
∴a = 已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。 ∵N(1,0)关于对称轴 x = -1的对称点的坐标为(-3,0) 设抛物线解析式为 把(-1,-2)代入,得
抛物线的解析式为
即解法三:交点式求二次函数解析式的一般方法: 已知图象上三点坐标或三对对应值,
通常选择一般式 已知图象的顶点坐标(或对称轴和最值)
通常选择顶点式 已知图象与x轴的两个交点的横坐标x1、x2,
通常选择交点式确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式. 课堂小结若不共线三点的横坐标两两不相等,
则经过这三点可以确定一个二次函数。
可以证明:二次函数的图像上任意三
个不同的点都不在一条直线上。谢 谢!
恳请各位同仁多多指教!
2.学会用待定系数法求经过不共线三点确定的二次函数解析式;
3.体会数形结合的思想方法;
4.感受数学的无穷魅力,体验合作交流探索数学的乐趣.1、一次函数图象经过(2,3)和(-1,-3)
两点,求这个一次函数的解析式? 复习与思考右图为一个二次函数的图像,根据图像提供的信息,
请你写出这个二次函数的相关结论,同学们比一比,
看谁写得多.2、动脑筋,想一想(1)二次函数图像开口向上(2)顶点坐标是(1,-1),
对称轴是x=1(3)当x=1时,函数有最小值-1(4)当x>1时,y随x的增大而增大,
当x<1时,y随x的增大而减小(5)函数图像与x轴交于点(0,0)、(2,0)(6)函数图像经过第一、二、四象限你还能求得这个二次函数其它哪些结论?3、二次函数的解析式有哪些形式?1、一般式2、顶点式3、交点式 和 是抛物线与x轴的两个交点坐标! 顶点坐标是(h,k)例1 二次函数的图象经过点A(-1,10)、
B(1,4)和C(2,7),求这个二次函数的
解析式.一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=ax2+bx+c由条件得:a-b+c=10
a+b+c=4
4a+2b+c=7解方程组得:∴所求二次函数是a=2, b=-3, c=5y=2x2-3x+5已知二次函数图象上的三个点的坐标或三对对应值时,通常设
一般式!x=-1时,y=10;
x=1时,y=4;
x=2时,y=7;解: ∴存在二次函数为y=x2-2x-3例2、是否有一个二次函数,它的图象过
三点(0,-3), (4,5),(-1, 0)?∵二次函数的图象过点(0,-3)(4,5)(-1, 0)∴设有二次函数为 y=ax2+bx+c符合题意例2表明:若给定不共线三点的坐标,
且它们的横坐标两两不相等,
则经过这三点可以确定一个二次函数。
可以证明:二次函数的图像上任意三
个不同的点都不在一条直线上。练习1:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.解:设存在二次函数为y=ax2+bx+c由已知,这个函数的图象过(0,1),可以得到c=1又由于其图象过(2,4)、(3,10)两点,可以得到解这个方程组,得:所以,存在二次函数的关系式是练习2、是否有一个二次函数,它的图象过
三点(0,1), (2,4),(3, 10)?例3 已知抛物线的顶点为(-1,-3),与y
轴交点为(0,-5),求抛物线的解析式?一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=a(x+1)2-3∵点( 0, -5 )在抛物线上,∴a-3=-5, 得a=-2∴所求的抛物线解析式为
y=-2(x+1)2-3即 y=-2x2-4x-5
已知二次函数图象的顶点的坐标时,通常设顶点式!练习3:
已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?∵点( 0,-3)在抛物线上∴a-4=-3, ∴所求的抛物线解析式为 y=(x-1)2-4 a=1x=1,y最值=-4已知条件中的当x=1时有最值-4
也就是抛物线的顶点坐标为(1,-4),
所以设为顶点式较方便例4 已知抛物线与x轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?一般式: y=ax2+bx+c交点式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=a(x+1)(x-1)∵点M( 0,1 )在抛物线上,∴a(0+1)(0-1)=1得 a=-1∴所求的抛物线解析式为
y=-(x+1)(x-1)即 y=-x2+1
已知二次函数图象与x轴的两个交点的横坐标时,通常设
交点式!练习4:已知抛物线与x轴两交点横坐标为1,3,且图像过(0,-3),求出对应的二次函数解析式。解:设所求的二次函数为y=a(x-1)(x-3),已知抛物线与x轴的交点
或交点横坐标时,通常
设为交点式(两根式)∵过点(0,-3),∴ a(0-1)(0-3)=-3,∴a=-1∴ y=-(x-1)(x-3),即y=-x2+4x-3例5、已知二次函数 的图像如图所示,
求其解析式。解法一: 一般式∴ 应用举例设解析式为 即:解得例5、已知二次函数 的图像如图所示,
求其解析式。解法二:顶点式∵顶点C(1,4)又∵A(-1,0)在抛物线上, ∴ a = -1 应用举例设解析式为解法三:交点式∵抛物线与x 轴的两个交点坐标
为 A (-1,0)、B(3,0)∴设解析式为y = a (x+1) (x- 3)又 C(1,4)在抛物线上∴ 4 = a (1+1) (1-3)∴ a = -1 ∴ y = - ( x+1) (x-3)例5、已知二次函数 的图像如图所示,
求其解析式。 应用举例∵对称轴 x=1.∴A(-1,0)关于 x=1的对称点B(3,0)。 你能用几种方法求出右图对应的二次函数解析式只要求列式1、观察下列条件,说出求解析式的方法⑴抛物线经过(0,-5)(5,0)两点,对称轴是直线 x = 2⑵二次函数图象经过(0,4),且当 x = 1时,函数值为3;当 x = -1时,函数值为4⑶抛物线的顶点坐标为(2,4),且经过原点⑷抛物线经过点(0,-4),且当 x = 2时,函数图象最高点的纵坐标是4当堂测试你该怎样设?已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。2、你能用几种方法求解解法一: 一般式解得已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。 解:设此抛物线的解析式为:解法二:顶点式∵过点 N(1,0)∴0 = 4a – 2
∴a = 已知抛物线顶点为M(-1,-2),且过点N(1,0),求此二次函数解析式。 ∵N(1,0)关于对称轴 x = -1的对称点的坐标为(-3,0) 设抛物线解析式为 把(-1,-2)代入,得
抛物线的解析式为
即解法三:交点式求二次函数解析式的一般方法: 已知图象上三点坐标或三对对应值,
通常选择一般式 已知图象的顶点坐标(或对称轴和最值)
通常选择顶点式 已知图象与x轴的两个交点的横坐标x1、x2,
通常选择交点式确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式. 课堂小结若不共线三点的横坐标两两不相等,
则经过这三点可以确定一个二次函数。
可以证明:二次函数的图像上任意三
个不同的点都不在一条直线上。谢 谢!
恳请各位同仁多多指教!
