1.4 二次函数与一元二次方程的联系 课件 (2)15张
文档属性
| 名称 | 1.4 二次函数与一元二次方程的联系 课件 (2)15张 |

|
|
| 格式 | zip | ||
| 文件大小 | 302.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 00:00:00 | ||
图片预览






文档简介
课件15张PPT。1.4 二次函数与一元二次方程的联系探究:画出二次函数y=x2-2x-3的图象,你能从图象中看出它与x轴的交点吗?
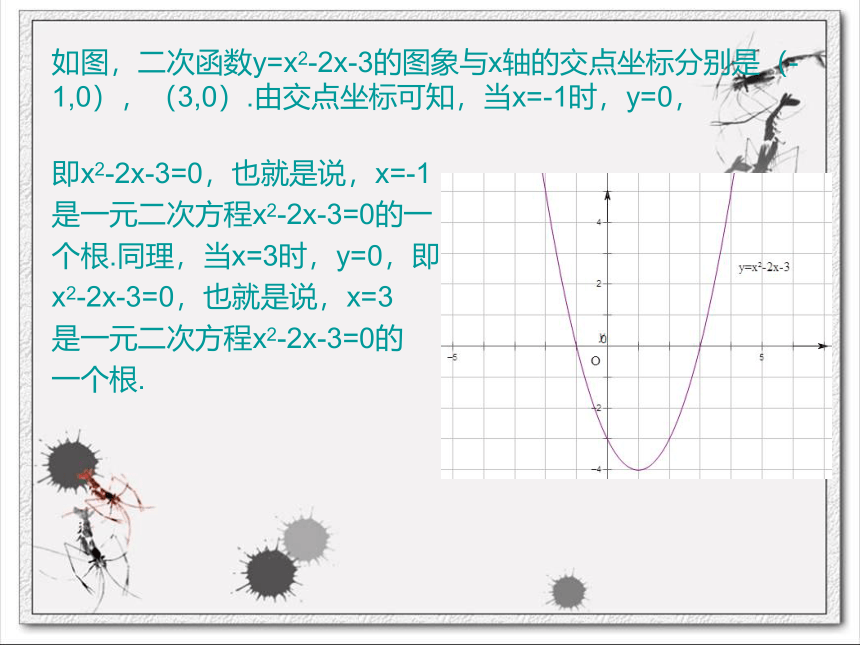
二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系?如图,二次函数y=x2-2x-3的图象与x轴的交点坐标分别是(-1,0),(3,0).由交点坐标可知,当x=-1时,y=0,即x2-2x-3=0,也就是说,x=-1
是一元二次方程x2-2x-3=0的一
个根.同理,当x=3时,y=0,即
x2-2x-3=0,也就是说,x=3
是一元二次方程x2-2x-3=0的
一个根.小结:一般地,如果二次函数y=ax2+bx+c(a≠0)的图象与x轴
有两个不同的交点(x1,0),(x2,0),那么一元二次方
程ax2+bx+c=0有两个不相等的实根x=x1,x=x2.动脑筋:观察二次函数y=x2-6x+9,y=x2-2x+2的图象(如图)
,分别说出一元二次方程x2-6x+9=0,x2-2x+2=0的根的情况.
二次函数y=x2-6x+9的图象与
x轴有重合的两个交点,其坐
标都是(3,0),而一元二次
方程x2-6x+9=0有两个相等的
实根,x1=3,x2=3.
二次函数y=x2-2x+2的图象与
x轴没有交点,而一元二次方
程x2-2x+2=0没有实数根.
小结:一般地,二次函数y=ax2+bx+c(a≠0)的图象与x轴的位置关系有三种:有两个不同的交点、有两个重合的交点、没有交点.这对应着ax2+bx+c=0(a≠0)的根三种情况:有两个不相等的实根、有两个相等的实根和没有实数根.反过来,由一元二次方程根的情况,也可以确定相应的图象与x轴的位置关系.
从上面的分析可知,我们可以利用二次函数的图象来求一元二次方程的根,由于作图或者观察的误差,由图象求得的根,一般是近似的.求一元二次方程 的解的近似值(精确到0.1) 从例1受到启发,一元二次方程 的解就是:抛物线 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.从图量得抛物线与x轴的交点的横坐标约为-0.4或2.4,因此方程 的解的近似值为-0.4或2.4描点和连线:画出图象在对称轴右边的部分.利用对称性画出图象在对称轴左边的部分,这就得到了的图象,如图例2 如图,丁丁在扔铅球时,铅球沿抛物线 运行 ,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.(1)当铅球离地面的高度为2.1m时,它离初始位置的水平
距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达到3m?为什么?解 (1)由抛物线的表达式得 即x2-6x+5=0,解得x1=1,x2=5.即当铅球离地面的高度为2.1时,它离初始位置的水平距离是1m或5m.
(2)由抛物线的表达式得
即x2-6x+9=0,解得x1=x2=3.
当铅球离地面的高度为2.5时,它离初始位置的水平距离是3m.
(3)由抛物线的表达式得
即x2-6x+14=0,因为△=(-6)2-4×1×14<0,所以方程无实数根.
所以铅球离地面的高度不能达到3m.1.求下列抛物线与x轴的交点的横坐标:它与x轴有交点,则y=0解这个方程 (x-2)(x+1)= 0∴ x1=2, x2=-1∴ 与x轴交点的横坐标为(2,0)(-1,0)解它与x轴有交点,则y=0∴ x1= x2=∴ 与x轴交点的横坐标为( ,0)解它与x轴有交点,则y=0∴ x=1∴ 与x轴交点的横坐标为( 1 ,0)解3.用图象法求一元二次方程 的解的近似值(精确到0.1)解:设二次函数y=x2+x-1
做出二次函数y=x2+x-1的图象如图所示通过观察图象可知,抛物线与x轴的交点坐标约为x1=-1.6,x2=0.6.即一元二次方程x2+x-1=0的实数根为x1≈-1.6,x2≈0.6.
结束寄语生活是数学的源泉.再见探索是数学的生命线.
二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系?如图,二次函数y=x2-2x-3的图象与x轴的交点坐标分别是(-1,0),(3,0).由交点坐标可知,当x=-1时,y=0,即x2-2x-3=0,也就是说,x=-1
是一元二次方程x2-2x-3=0的一
个根.同理,当x=3时,y=0,即
x2-2x-3=0,也就是说,x=3
是一元二次方程x2-2x-3=0的
一个根.小结:一般地,如果二次函数y=ax2+bx+c(a≠0)的图象与x轴
有两个不同的交点(x1,0),(x2,0),那么一元二次方
程ax2+bx+c=0有两个不相等的实根x=x1,x=x2.动脑筋:观察二次函数y=x2-6x+9,y=x2-2x+2的图象(如图)
,分别说出一元二次方程x2-6x+9=0,x2-2x+2=0的根的情况.
二次函数y=x2-6x+9的图象与
x轴有重合的两个交点,其坐
标都是(3,0),而一元二次
方程x2-6x+9=0有两个相等的
实根,x1=3,x2=3.
二次函数y=x2-2x+2的图象与
x轴没有交点,而一元二次方
程x2-2x+2=0没有实数根.
小结:一般地,二次函数y=ax2+bx+c(a≠0)的图象与x轴的位置关系有三种:有两个不同的交点、有两个重合的交点、没有交点.这对应着ax2+bx+c=0(a≠0)的根三种情况:有两个不相等的实根、有两个相等的实根和没有实数根.反过来,由一元二次方程根的情况,也可以确定相应的图象与x轴的位置关系.
从上面的分析可知,我们可以利用二次函数的图象来求一元二次方程的根,由于作图或者观察的误差,由图象求得的根,一般是近似的.求一元二次方程 的解的近似值(精确到0.1) 从例1受到启发,一元二次方程 的解就是:抛物线 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.从图量得抛物线与x轴的交点的横坐标约为-0.4或2.4,因此方程 的解的近似值为-0.4或2.4描点和连线:画出图象在对称轴右边的部分.利用对称性画出图象在对称轴左边的部分,这就得到了的图象,如图例2 如图,丁丁在扔铅球时,铅球沿抛物线 运行 ,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.(1)当铅球离地面的高度为2.1m时,它离初始位置的水平
距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达到3m?为什么?解 (1)由抛物线的表达式得 即x2-6x+5=0,解得x1=1,x2=5.即当铅球离地面的高度为2.1时,它离初始位置的水平距离是1m或5m.
(2)由抛物线的表达式得
即x2-6x+9=0,解得x1=x2=3.
当铅球离地面的高度为2.5时,它离初始位置的水平距离是3m.
(3)由抛物线的表达式得
即x2-6x+14=0,因为△=(-6)2-4×1×14<0,所以方程无实数根.
所以铅球离地面的高度不能达到3m.1.求下列抛物线与x轴的交点的横坐标:它与x轴有交点,则y=0解这个方程 (x-2)(x+1)= 0∴ x1=2, x2=-1∴ 与x轴交点的横坐标为(2,0)(-1,0)解它与x轴有交点,则y=0∴ x1= x2=∴ 与x轴交点的横坐标为( ,0)解它与x轴有交点,则y=0∴ x=1∴ 与x轴交点的横坐标为( 1 ,0)解3.用图象法求一元二次方程 的解的近似值(精确到0.1)解:设二次函数y=x2+x-1
做出二次函数y=x2+x-1的图象如图所示通过观察图象可知,抛物线与x轴的交点坐标约为x1=-1.6,x2=0.6.即一元二次方程x2+x-1=0的实数根为x1≈-1.6,x2≈0.6.
结束寄语生活是数学的源泉.再见探索是数学的生命线.
