2.1 圆的对称性 课件 (1)(12PPT)
文档属性
| 名称 | 2.1 圆的对称性 课件 (1)(12PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 922.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 22:05:35 | ||
图片预览

文档简介
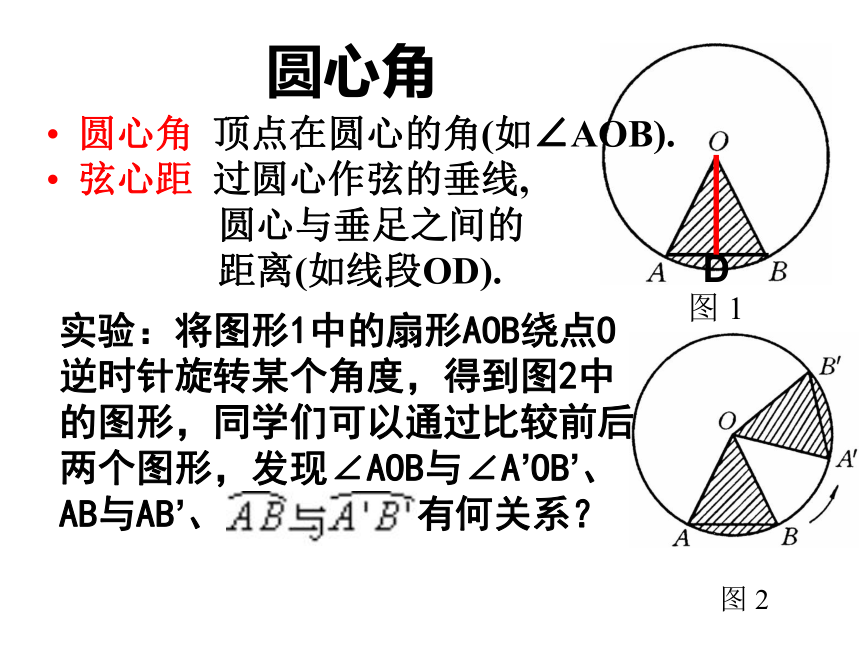
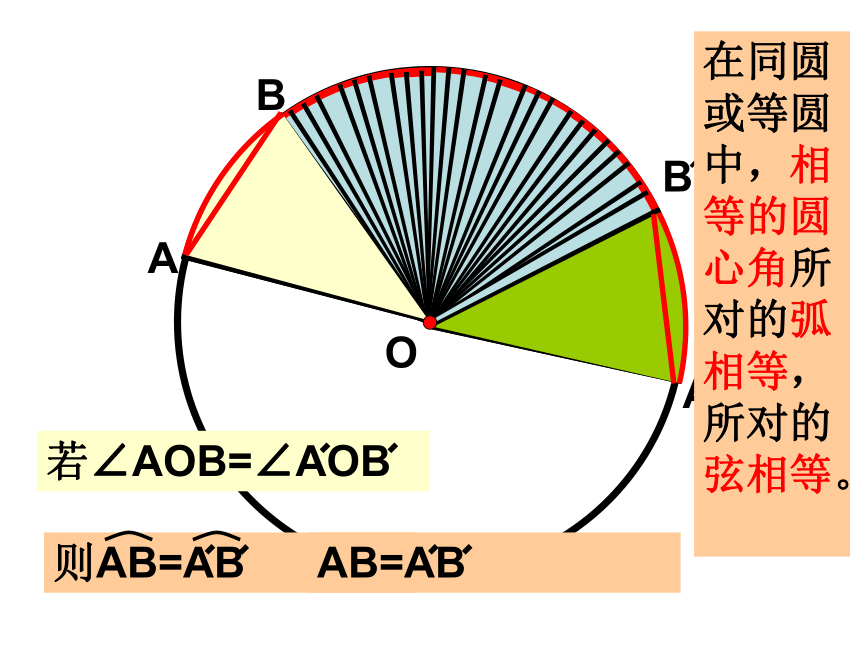
课件12张PPT。圆的对称性圆是轴对称图形,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,圆是旋转对称图形.实验:将图形1中的扇形AOB绕点O逆时针旋转某个角度,得到图2中的图形,同学们可以通过比较前后两个图形,发现∠AOB与∠A’OB’、AB与AB’、 有何关系?目标导学1:圆心角圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
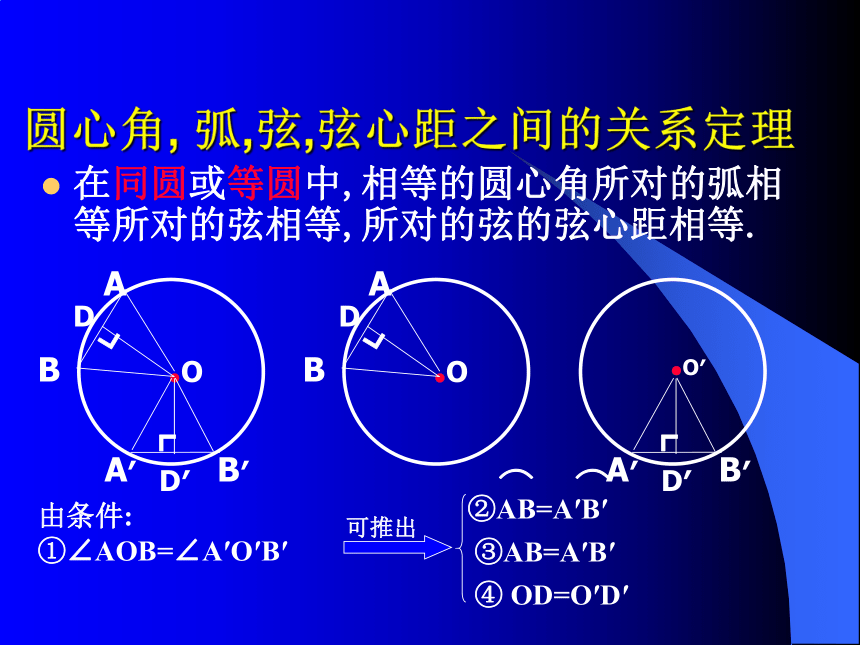
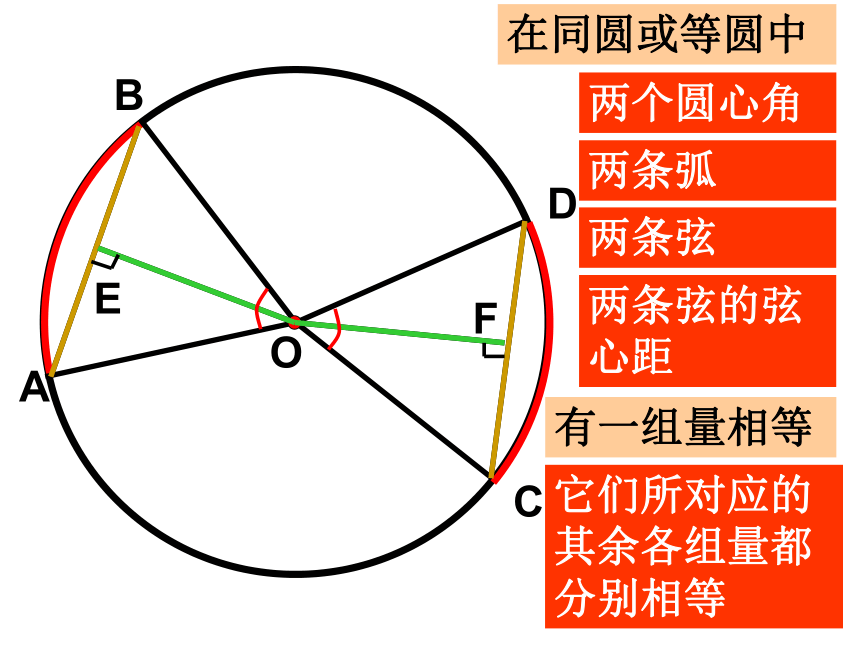
距离(如线段OD).OAB若∠AOB=∠AOB则AB=ABAB=AB在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ABODCEF在同圆或等圆中两个圆心角两条弧两条弦两条弦的弦心距有一组量相等它们所对应的其余各组量都分别相等一.判断下列说法是否正确:
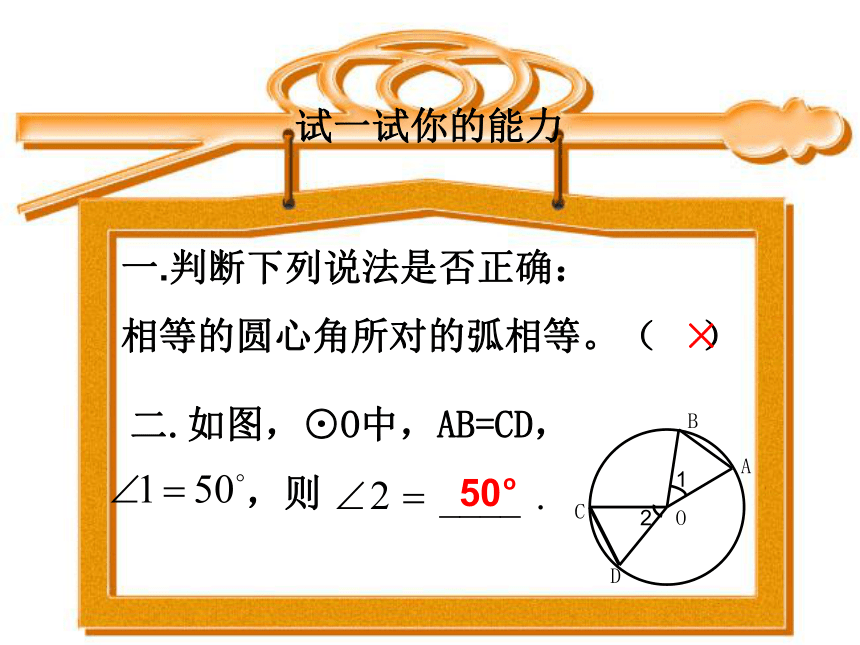
相等的圆心角所对的弧相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力×1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.你会做吗?2、如图,AB是直径,
BC=CD=DE,∠BOC=40°
则∠AOE= 。1、已知A、B是⊙O上的两点,∠AOB=120°,
C是弧AB的中点,试确定四边形OACB的形
状,并说明理由。2、在平行四边形ABCD中,以A为圆心,AB长为半径的圆分别交AD、BC于F、G,交BA的延长线于E,求证:EF=FGOPABCD例:如图,P是⊙O外一点,射线PAB,PCD分别交⊙O于A、B和C、D,已知AB=CD,求证:PO平分∠BPDFE3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM12343、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM34123、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
距离(如线段OD).OAB若∠AOB=∠AOB则AB=ABAB=AB在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ABODCEF在同圆或等圆中两个圆心角两条弧两条弦两条弦的弦心距有一组量相等它们所对应的其余各组量都分别相等一.判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力×1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.你会做吗?2、如图,AB是直径,
BC=CD=DE,∠BOC=40°
则∠AOE= 。1、已知A、B是⊙O上的两点,∠AOB=120°,
C是弧AB的中点,试确定四边形OACB的形
状,并说明理由。2、在平行四边形ABCD中,以A为圆心,AB长为半径的圆分别交AD、BC于F、G,交BA的延长线于E,求证:EF=FGOPABCD例:如图,P是⊙O外一点,射线PAB,PCD分别交⊙O于A、B和C、D,已知AB=CD,求证:PO平分∠BPDFE3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM12343、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM34123、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB
