2.1 圆的对称性 课件 (3)(30PPT)
文档属性
| 名称 | 2.1 圆的对称性 课件 (3)(30PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 00:00:00 | ||
图片预览










文档简介
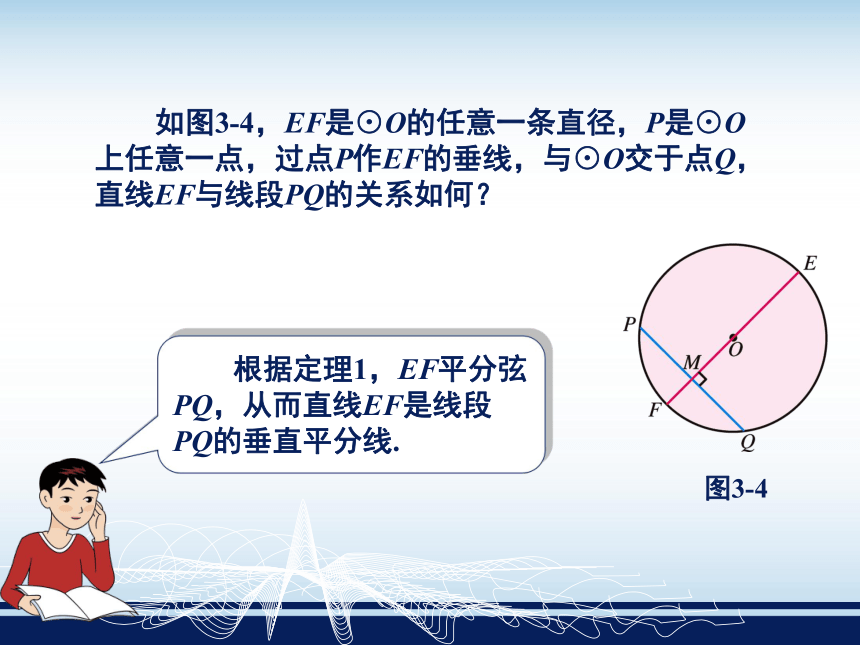
课件30张PPT。圆2.1——2.1.1 圆的对称性 图3-1是国际奥林匹克运动会旗的标志图案. 用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合.这两个圆 . 现在用一根大头针穿过这两个圆的圆心. 让硬纸板保持不动,让白纸绕圆心旋转任意角度. 观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合.这体现圆具有什么样的性质? 能够重合的两个圆叫做相等的圆,或等圆. 在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.这体现圆具有什么样的对称性? 观察圆的两部分是否互相重合. 你能讲出圆具有这种对称性的道理吗?例1 已知:如图3-3,在⊙O中,直径CD与
弦AB垂直,垂足为E.
求证:AE=BE . 证明 连结 OA,OB. 由于 OA=OB,因此△OAB是等腰三角形. 又OE是底边AB上的高,因而OE也是底边AB上的中线. 从而AE=BE.定理1 垂直于弦的直径平分这条弦. 现在你能说出道理吗? 为什么圆的任意一条直径所在的直线是它的对称轴? 如图3-4,EF是⊙O的任意一条直径,P是⊙O上任意一点,过点P作EF的垂线,与⊙O交于点Q,直线EF与线段PQ的关系如何? 根据定理1,EF平分弦PQ,从而直线EF是线段PQ的垂直平分线. 于是点P与点Q关于直线EF对称,因此,圆O关于直线EF对称. 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴. 1. 自行车的车轱辘是圆形,为什么?答:车轱辘(圆周)上的任意一点到轴
(圆心)的距离都相等(半径).
2. 下述命题是否正确?为什么?(1)平分弦(不是直径)的直径垂直于这条弦;(2)圆只有一条对称轴;答:正确.
因为平分非直径的弦的直径所在的
直线是这条弦的对称轴.答:不正确.
圆的任何一条直径所在的直线都是
圆的对称轴.(3)圆的任意一条弦是圆的对称轴;(4)圆既是中心对称图形,又是轴对称图形.答:不正确. 答:正确. 3. 已知⊙O的半径为5 cm,弦AB的长为6 cm,
求圆心到AB的距离.答:在⊙O中半径r=5 cm,AB=6 cm,
作直径垂直平分于AB,交AB于点M,
所以AM=MB=3 cm.
所以在Rt△AMO中,
AO=5cm,AM=3 cm,
所以OM=4 cm.
即圆心到AB的距离为4 cm. 圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“︵”表示,如图3-5(1),圆O上两点A,B间的小于半圆的部分叫做劣弧,记做 ;A,B间的大于半圆的部分叫做优弧,记做 ,其中M是圆上一点.
如图3-5(1),∠AOB叫做 所对的圆心角, 叫做圆心角∠AOB所对的弧.
在生活中,我们常遇到圆心角,如飞靶(图3-5(2))中有圆心角,还有手表中的时针与分针所成的角也是圆心角. 在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等. 在同一个圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗?你能讲出道理吗? 在同一个圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?你能讲出道理吗? 垂直于弦的直径平分这条弦所对的两条弧吗? 如图3-7,直径CD垂直于弦AB. 根据定理1可得,直线CD是线段AB的垂直平分线,从而点A与点B关于直线CD对称.垂直于弦的直径平分这条弦所对的两条弧.证明 作直径EF垂直于弦AB,由于AB∥CD,因此EF⊥CD.由于EF⊥AB,由于EF⊥CD, 1. 如图3-9,圆O中,AB∥CD.
求证:∠AOC=∠BOD.答∵ AB∥CD.∴ ∠AOC=∠BOD.(由例题结论得)2. 如图3-9,圆O中,AB∥CD.
求证:AC=BD.例1A
弦AB垂直,垂足为E.
求证:AE=BE . 证明 连结 OA,OB. 由于 OA=OB,因此△OAB是等腰三角形. 又OE是底边AB上的高,因而OE也是底边AB上的中线. 从而AE=BE.定理1 垂直于弦的直径平分这条弦. 现在你能说出道理吗? 为什么圆的任意一条直径所在的直线是它的对称轴? 如图3-4,EF是⊙O的任意一条直径,P是⊙O上任意一点,过点P作EF的垂线,与⊙O交于点Q,直线EF与线段PQ的关系如何? 根据定理1,EF平分弦PQ,从而直线EF是线段PQ的垂直平分线. 于是点P与点Q关于直线EF对称,因此,圆O关于直线EF对称. 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴. 1. 自行车的车轱辘是圆形,为什么?答:车轱辘(圆周)上的任意一点到轴
(圆心)的距离都相等(半径).
2. 下述命题是否正确?为什么?(1)平分弦(不是直径)的直径垂直于这条弦;(2)圆只有一条对称轴;答:正确.
因为平分非直径的弦的直径所在的
直线是这条弦的对称轴.答:不正确.
圆的任何一条直径所在的直线都是
圆的对称轴.(3)圆的任意一条弦是圆的对称轴;(4)圆既是中心对称图形,又是轴对称图形.答:不正确. 答:正确. 3. 已知⊙O的半径为5 cm,弦AB的长为6 cm,
求圆心到AB的距离.答:在⊙O中半径r=5 cm,AB=6 cm,
作直径垂直平分于AB,交AB于点M,
所以AM=MB=3 cm.
所以在Rt△AMO中,
AO=5cm,AM=3 cm,
所以OM=4 cm.
即圆心到AB的距离为4 cm. 圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“︵”表示,如图3-5(1),圆O上两点A,B间的小于半圆的部分叫做劣弧,记做 ;A,B间的大于半圆的部分叫做优弧,记做 ,其中M是圆上一点.
如图3-5(1),∠AOB叫做 所对的圆心角, 叫做圆心角∠AOB所对的弧.
在生活中,我们常遇到圆心角,如飞靶(图3-5(2))中有圆心角,还有手表中的时针与分针所成的角也是圆心角. 在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等. 在同一个圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗?你能讲出道理吗? 在同一个圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?你能讲出道理吗? 垂直于弦的直径平分这条弦所对的两条弧吗? 如图3-7,直径CD垂直于弦AB. 根据定理1可得,直线CD是线段AB的垂直平分线,从而点A与点B关于直线CD对称.垂直于弦的直径平分这条弦所对的两条弧.证明 作直径EF垂直于弦AB,由于AB∥CD,因此EF⊥CD.由于EF⊥AB,由于EF⊥CD, 1. 如图3-9,圆O中,AB∥CD.
求证:∠AOC=∠BOD.答∵ AB∥CD.∴ ∠AOC=∠BOD.(由例题结论得)2. 如图3-9,圆O中,AB∥CD.
求证:AC=BD.例1A
