2.3 垂径定理 课件 (5)(15张PPT)
文档属性
| 名称 | 2.3 垂径定理 课件 (5)(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 884.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 10:12:10 | ||
图片预览






文档简介
课件15张PPT。垂径定理问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 问题情境 把一个圆沿着它的任意一条直径对折,
重复几次,你发现了什么?由此你能得到
什么结论?可以发现:
圆是轴对称图形,任何一条
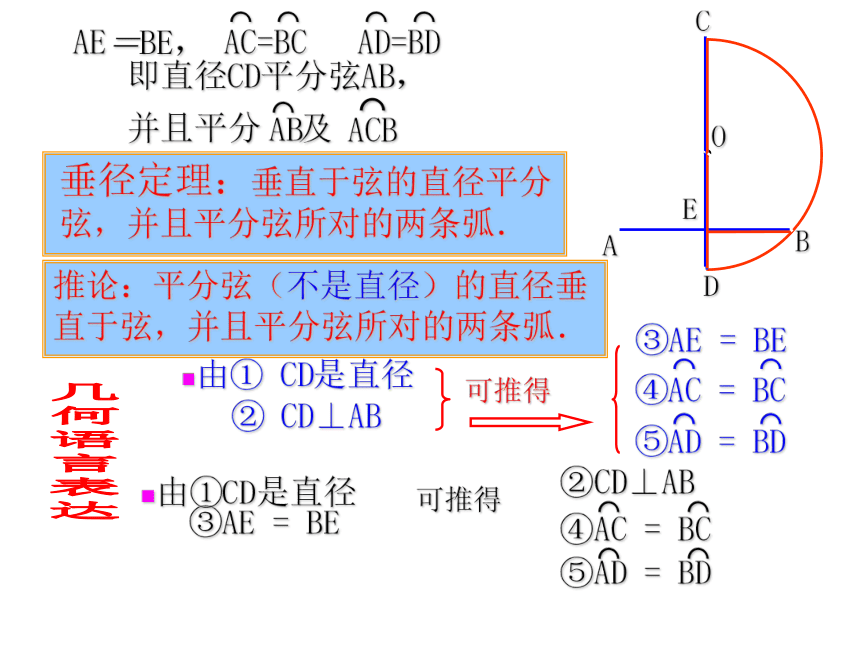
直径所在直线都是它的对称轴. 活动一·OABCDE(1)是轴对称图形.直径CD所在
的直线是它的对称轴(2)线段:AE=BE活动二·OABCDE几
何
语
言
表
达辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件?解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2 = AD2 + OD2OD = OC-CD = R-7.2在图中 AB=37.4,CD=7.2,1.如图,在⊙O中,弦AB的长为8cm,圆心O
到AB的距离为3cm,求⊙O的半径.练习答:⊙O的半径为5 cm。活动三2.如图,在⊙O中,AB、AC为互相垂直且相等的
两条弦,OD⊥AB于D,OE⊥AC于E,求证四边
形ADOE是正方形.又 ∵AC = AB∴ AE = AD∴ 四边形ADOE为正方形。巩固训练判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分 活动三练习4、弓形的弦长为6cm,弓形的高为2cm,
则这弓形所在的圆的半径为 . 活动三练习 5、已知P为⊙ O内一点,且OP=2cm,如果
⊙ O的半径是3cm,那么过P点的最短的
弦等于 .
活动三练习说一说1、本节课你学到了哪些数学知识?
2、在利用垂径定理解决问题时,你
掌握了哪些数学方法?再见
重复几次,你发现了什么?由此你能得到
什么结论?可以发现:
圆是轴对称图形,任何一条
直径所在直线都是它的对称轴. 活动一·OABCDE(1)是轴对称图形.直径CD所在
的直线是它的对称轴(2)线段:AE=BE活动二·OABCDE几
何
语
言
表
达辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件?解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2 = AD2 + OD2OD = OC-CD = R-7.2在图中 AB=37.4,CD=7.2,1.如图,在⊙O中,弦AB的长为8cm,圆心O
到AB的距离为3cm,求⊙O的半径.练习答:⊙O的半径为5 cm。活动三2.如图,在⊙O中,AB、AC为互相垂直且相等的
两条弦,OD⊥AB于D,OE⊥AC于E,求证四边
形ADOE是正方形.又 ∵AC = AB∴ AE = AD∴ 四边形ADOE为正方形。巩固训练判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分 活动三练习4、弓形的弦长为6cm,弓形的高为2cm,
则这弓形所在的圆的半径为 . 活动三练习 5、已知P为⊙ O内一点,且OP=2cm,如果
⊙ O的半径是3cm,那么过P点的最短的
弦等于 .
活动三练习说一说1、本节课你学到了哪些数学知识?
2、在利用垂径定理解决问题时,你
掌握了哪些数学方法?再见
