2.3 垂径定理 课件 (7)(29PPT)
文档属性
| 名称 | 2.3 垂径定理 课件 (7)(29PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 11:15:32 | ||
图片预览



文档简介
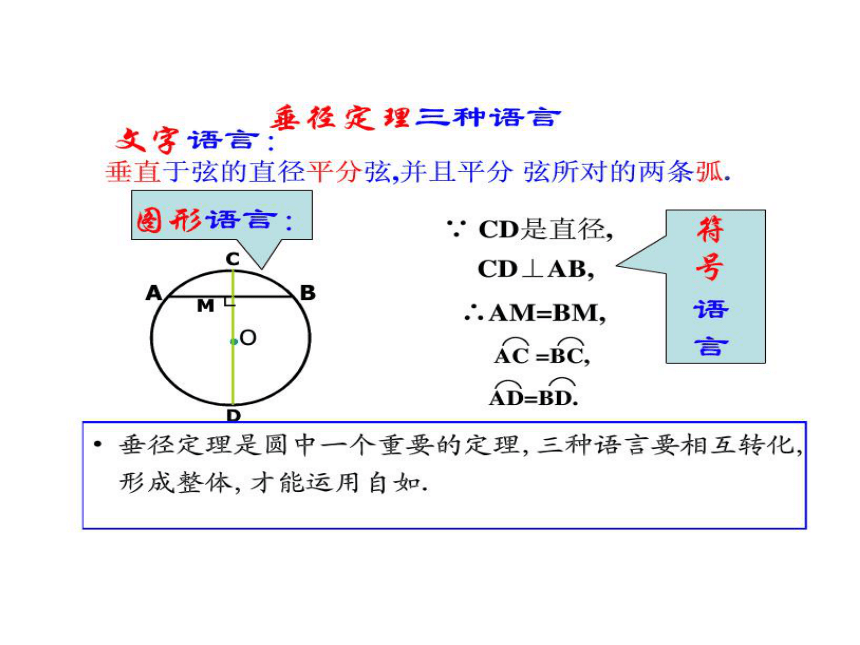
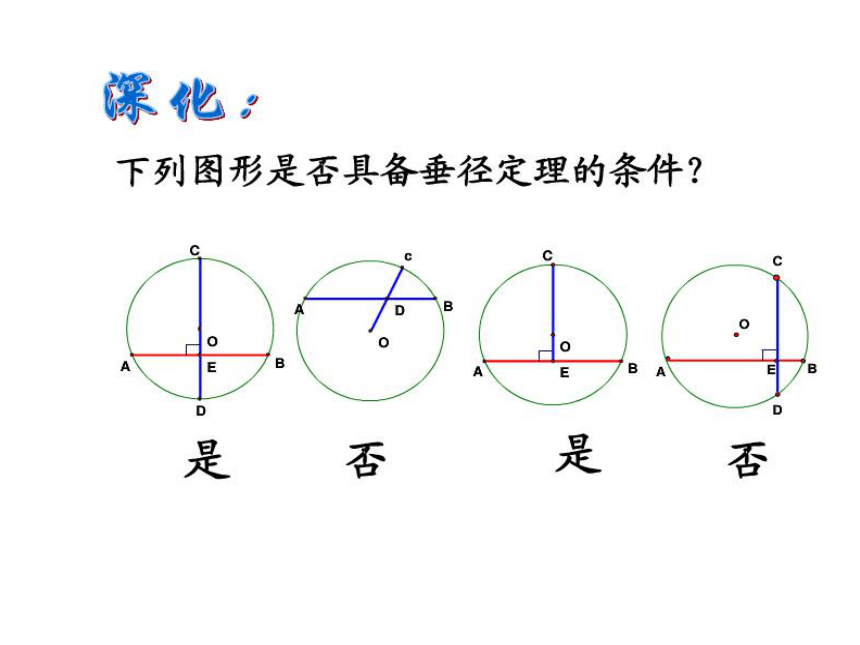
课件29张PPT。§2.3 垂径定理你熟悉下列图片吗?若已知三桥的跨度和拱高,你能求出桥拱所在圆的半径吗?┗例2、如图,AB、CD都是⊙O的弦,且AB∥CD.
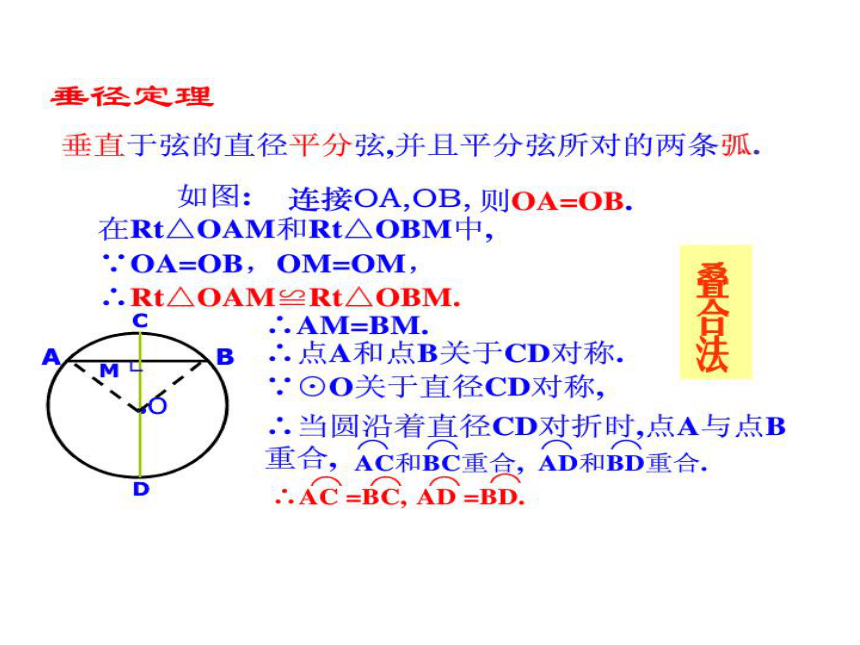
求证:AC = BD。 FE解:过点O作OE⊥CD,交CD于点E在⊙O中,OF⊥弦ABG交⊙O于点G交AB于点F,∵ OE⊥弦CDGabcd∵ a = b ,c = d∴ a – c = b - d线段加减圆弧加减 根据垂径定理可知:对于一个圆和一条直线来说,如果具备: 那么,由五个条件中的任何两个条件都可以推出其他三个结论。注意要点① 经过圆心② 垂直于弦 ③ 平分弦④ 平分弦所对的优弧⑤ 平分弦所对的劣弧(1)垂直于弦的直线平分弦,并且平分弦所对的弧。 ……………………… ( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心。 …………………… ( )(3)圆的不与直径垂直的弦必不被这条直径平分。………………………………… ( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。 …………………………… ( )(5)圆内两条非直径的弦不能互相平分。( )×√××√判断正误(2-1)强化记忆(3-1) 垂直于弦的直径平分这条弦;并且平分弦所对的两条弧。 垂径定理圆的两条平行弦所夹的弧相等。 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。1、在⊙O中,OC垂直于弦AB,AB = 8,
OA = 5,则AC = ,OC = 。┏58431、在⊙O中,OC平分弦AB,AB = 16,
OA = 10,则∠OCA = °,OC = 。1610906作业评讲 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB。
解:连接OA在⊙O中,直径CD⊥弦AB∴ AB =2AM△OMA是 △∵ CD = 20∴ AO = CO = 10∴ OM = OC – CM = 10 – 4 = 6在Rt △OMA中,AO = 10,OM = 6根据勾股定理,得:∴∴ AB = 2AM = 2 x 8 = 162、如图4,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD求证:△OCD为等腰三角形。
3、如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 4.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 :
.
图中相等的劣弧有:
.5、已知:如图,⊙O 中, AB为 弦,C 为
弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.6.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.MN已知:AB和CD是⊙O内的两条平行弦,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2)
求证:AC = BD。 FE解:过点O作OE⊥CD,交CD于点E在⊙O中,OF⊥弦ABG交⊙O于点G交AB于点F,∵ OE⊥弦CDGabcd∵ a = b ,c = d∴ a – c = b - d线段加减圆弧加减 根据垂径定理可知:对于一个圆和一条直线来说,如果具备: 那么,由五个条件中的任何两个条件都可以推出其他三个结论。注意要点① 经过圆心② 垂直于弦 ③ 平分弦④ 平分弦所对的优弧⑤ 平分弦所对的劣弧(1)垂直于弦的直线平分弦,并且平分弦所对的弧。 ……………………… ( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心。 …………………… ( )(3)圆的不与直径垂直的弦必不被这条直径平分。………………………………… ( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。 …………………………… ( )(5)圆内两条非直径的弦不能互相平分。( )×√××√判断正误(2-1)强化记忆(3-1) 垂直于弦的直径平分这条弦;并且平分弦所对的两条弧。 垂径定理圆的两条平行弦所夹的弧相等。 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。1、在⊙O中,OC垂直于弦AB,AB = 8,
OA = 5,则AC = ,OC = 。┏58431、在⊙O中,OC平分弦AB,AB = 16,
OA = 10,则∠OCA = °,OC = 。1610906作业评讲 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB。
解:连接OA在⊙O中,直径CD⊥弦AB∴ AB =2AM△OMA是 △∵ CD = 20∴ AO = CO = 10∴ OM = OC – CM = 10 – 4 = 6在Rt △OMA中,AO = 10,OM = 6根据勾股定理,得:∴∴ AB = 2AM = 2 x 8 = 162、如图4,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD求证:△OCD为等腰三角形。
3、如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 4.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 :
.
图中相等的劣弧有:
.5、已知:如图,⊙O 中, AB为 弦,C 为
弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.6.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.MN已知:AB和CD是⊙O内的两条平行弦,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2)
