2.4 过不共线三点作圆 课件 (5)(21PPT)
文档属性
| 名称 | 2.4 过不共线三点作圆 课件 (5)(21PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览








文档简介
课件21张PPT。义务教育教科书SHUXUE 九年级下册湖南教育出版社第2章 圆2.4 过不共线三点作圆教学目标:
(1)了解三角形的外接圆、三角形的外心
和圆的内接三角形的概念。
(2)理解定理“不在同一直线上的三个点
确定一个圆”。
(3)学会画三角形的外接圆。教学重点、难点: 重点:定理“不在同一直线上的三 个点确定一个圆”及圆的画法。
难点:论证“不在同一直线上的三个点确定一个圆”的推理过程。教学过程:一、复习提问:
1、什么叫圆?
2、确定一个圆的要素有哪些?
二、新授课
1、创设情境、提出问题
问题引入:(破镜重圆)现有一块打碎的圆形玻璃镜子残片,想重新去玻璃店配一块同样大小的圆形玻璃镜子,请问怎样去配制呢?
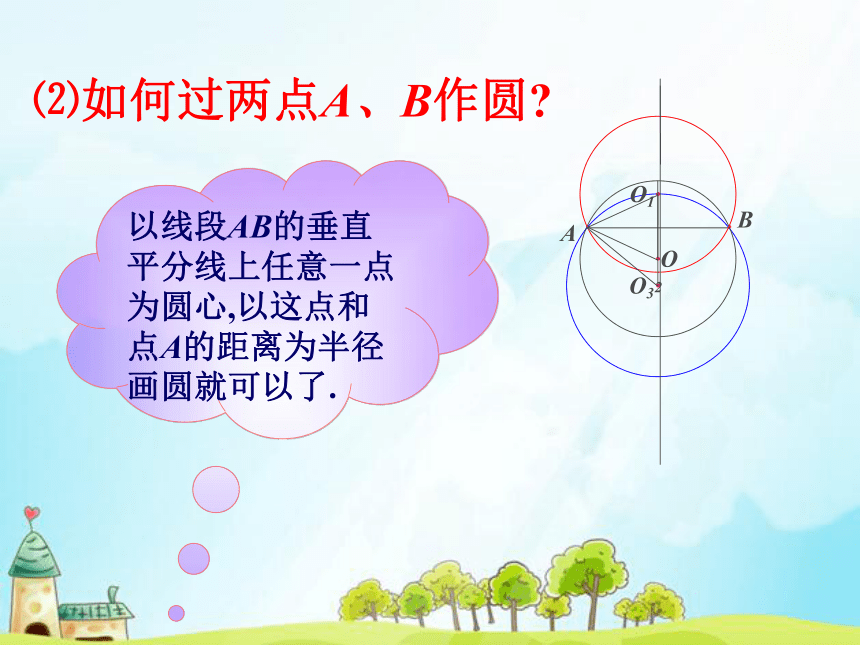
如何解决这一实际问题?下面我们共同探讨解决。探究1.如何过一点A作 一个圆? 只要以点A以外的任意一点为圆心,以这个点和点A的距离为半径画圆就可以了,如图.···O1O2O3过点A可以作多少个圆? ·A···2、过两点A、B能否作一个圆?由于两点A、B与圆心的距离相等,因此圆心在线段AB的垂直平分线上.··⑴过两点A、B的圆的圆心在哪儿?·O1O2··O3AB⑵如何过两点A、B作圆?以线段AB的垂直平分线上任意一点为圆心,以这点和点A的距离为半径画圆就可以了.···O1··O2··O3·AB⑶ 过两点A、B可以作多少个圆?过两点A、B可以作无数多个圆。如图.···O1··O2··O3·AB3.如何过不在同一直线上的三个点作圆?可以作多少个圆?设A、B、C是不在同一直线上三点.⑴过三点A、B、C的圆的圆心在哪儿?由于圆O与三点A,B,C的距离相等,因此圆心O既在线段AB的垂直平分线上,又在线段BC的垂直平分线上.则圆O就是所求作的圆.·A ·· OB
·· C⑵过不在同一直线上的三点A、B、C如何作圆?已知:不在同一直线上的三点A、B、C求作:圆O,使它经过点A、B、C.作法: ①连结AB,作线段AB和垂直平分线EF;②连结BC,作线段BC的垂平分线MN;③以EF和MN的交点O为圆心,以OB为半径作圆. 由于过不在同一直线上的三点A、B、C的圆,其圆心是线段AB的垂直平分线EF与线段BC的垂直平分线MN的交点O,半径OA,因此过不在同一直线上的三点A、B、C只能作一个圆.定理:不在同一直线上的三个点确定一个圆.⑶过不共线的三点A、B、C能作多少个圆?综上所述,我们证明了定理:它们有交点吗?由此可知,过同一直线上的三点A、B、C能作一个圆吗?4.过同直线上的三点A、B、C能作一个圆吗?线段AB的垂直平分线EF与线段BC的垂直平分线MN有什么关系?……EF∥MN 没有交点不能做圆ABC由于△ABC的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.说一说经过△ABC的三个顶点可以作一个圆吗? 可以作几个圆? 为什么? ·OCAB这个三角形叫作圆的内接三角形.从前面的讨论知道:三角形的外心是它的三条边的垂直平分线的交点.经过一个三角形各顶点的圆叫作这个三角形的外接圆。外接圆的圆心叫作这个三角形的外心··OCAB练习1.画一个三角形,作这个三角形的外接圆.·A ·· OB
·· C·BCA2.求边长为a的等边三角形的外接圆的半径.30°Rt △OBD中,有∠OBD=30° OD 应用新知(1)解决引例的问题(学生口述解决的办法)
①在残片上任取三点A、B、C,连结AB、AC
②分别作AB、AC的垂直平分线,并交于一
点O,O为圆心。
③连结OA,以OA为半径画圆即可。(2)判断 ①过两点可以作无数个圆。( )
②经过三点一定可以做一个圆。( )
③顶点都在圆上的三角形叫做圆的外接三角形。( )
④任意一个三角形一定有一个外接圆,并且只有一个外接圆。( )
⑤任意一个圆一定有一个内接三角形,并且只有一个内接三角形。( )
⑥三角形的外心就是这个三角形两边垂直平分线 的交点。( )
⑦三角形的外心到三边的距离相等。( )三、巩固与小结这节课我们主要学习了哪些具体内容?
这节课我们主要学习了哪些具体内容?
1、过一个点A能否作圆?如果能,可以作几个?
2、过两点A、B能否作圆?如果能,可以作几个? 圆心在哪里?
3、过同一平面内三个点A、B、C是否可以作圆?有几种情况呢?
4、三角形与圆的关系。
四、作业1、课本P.63 练习
2、作出下列三角形的外接圆,并比较这三个三角形的外心的位置,你得到什么结论?
(1)了解三角形的外接圆、三角形的外心
和圆的内接三角形的概念。
(2)理解定理“不在同一直线上的三个点
确定一个圆”。
(3)学会画三角形的外接圆。教学重点、难点: 重点:定理“不在同一直线上的三 个点确定一个圆”及圆的画法。
难点:论证“不在同一直线上的三个点确定一个圆”的推理过程。教学过程:一、复习提问:
1、什么叫圆?
2、确定一个圆的要素有哪些?
二、新授课
1、创设情境、提出问题
问题引入:(破镜重圆)现有一块打碎的圆形玻璃镜子残片,想重新去玻璃店配一块同样大小的圆形玻璃镜子,请问怎样去配制呢?
如何解决这一实际问题?下面我们共同探讨解决。探究1.如何过一点A作 一个圆? 只要以点A以外的任意一点为圆心,以这个点和点A的距离为半径画圆就可以了,如图.···O1O2O3过点A可以作多少个圆? ·A···2、过两点A、B能否作一个圆?由于两点A、B与圆心的距离相等,因此圆心在线段AB的垂直平分线上.··⑴过两点A、B的圆的圆心在哪儿?·O1O2··O3AB⑵如何过两点A、B作圆?以线段AB的垂直平分线上任意一点为圆心,以这点和点A的距离为半径画圆就可以了.···O1··O2··O3·AB⑶ 过两点A、B可以作多少个圆?过两点A、B可以作无数多个圆。如图.···O1··O2··O3·AB3.如何过不在同一直线上的三个点作圆?可以作多少个圆?设A、B、C是不在同一直线上三点.⑴过三点A、B、C的圆的圆心在哪儿?由于圆O与三点A,B,C的距离相等,因此圆心O既在线段AB的垂直平分线上,又在线段BC的垂直平分线上.则圆O就是所求作的圆.·A ·· OB
·· C⑵过不在同一直线上的三点A、B、C如何作圆?已知:不在同一直线上的三点A、B、C求作:圆O,使它经过点A、B、C.作法: ①连结AB,作线段AB和垂直平分线EF;②连结BC,作线段BC的垂平分线MN;③以EF和MN的交点O为圆心,以OB为半径作圆. 由于过不在同一直线上的三点A、B、C的圆,其圆心是线段AB的垂直平分线EF与线段BC的垂直平分线MN的交点O,半径OA,因此过不在同一直线上的三点A、B、C只能作一个圆.定理:不在同一直线上的三个点确定一个圆.⑶过不共线的三点A、B、C能作多少个圆?综上所述,我们证明了定理:它们有交点吗?由此可知,过同一直线上的三点A、B、C能作一个圆吗?4.过同直线上的三点A、B、C能作一个圆吗?线段AB的垂直平分线EF与线段BC的垂直平分线MN有什么关系?……EF∥MN 没有交点不能做圆ABC由于△ABC的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.说一说经过△ABC的三个顶点可以作一个圆吗? 可以作几个圆? 为什么? ·OCAB这个三角形叫作圆的内接三角形.从前面的讨论知道:三角形的外心是它的三条边的垂直平分线的交点.经过一个三角形各顶点的圆叫作这个三角形的外接圆。外接圆的圆心叫作这个三角形的外心··OCAB练习1.画一个三角形,作这个三角形的外接圆.·A ·· OB
·· C·BCA2.求边长为a的等边三角形的外接圆的半径.30°Rt △OBD中,有∠OBD=30° OD 应用新知(1)解决引例的问题(学生口述解决的办法)
①在残片上任取三点A、B、C,连结AB、AC
②分别作AB、AC的垂直平分线,并交于一
点O,O为圆心。
③连结OA,以OA为半径画圆即可。(2)判断 ①过两点可以作无数个圆。( )
②经过三点一定可以做一个圆。( )
③顶点都在圆上的三角形叫做圆的外接三角形。( )
④任意一个三角形一定有一个外接圆,并且只有一个外接圆。( )
⑤任意一个圆一定有一个内接三角形,并且只有一个内接三角形。( )
⑥三角形的外心就是这个三角形两边垂直平分线 的交点。( )
⑦三角形的外心到三边的距离相等。( )三、巩固与小结这节课我们主要学习了哪些具体内容?
这节课我们主要学习了哪些具体内容?
1、过一个点A能否作圆?如果能,可以作几个?
2、过两点A、B能否作圆?如果能,可以作几个? 圆心在哪里?
3、过同一平面内三个点A、B、C是否可以作圆?有几种情况呢?
4、三角形与圆的关系。
四、作业1、课本P.63 练习
2、作出下列三角形的外接圆,并比较这三个三角形的外心的位置,你得到什么结论?
