2.6 弧长与扇形面积 课件 (1)(20PPT)
文档属性
| 名称 | 2.6 弧长与扇形面积 课件 (1)(20PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 11:18:51 | ||
图片预览








文档简介
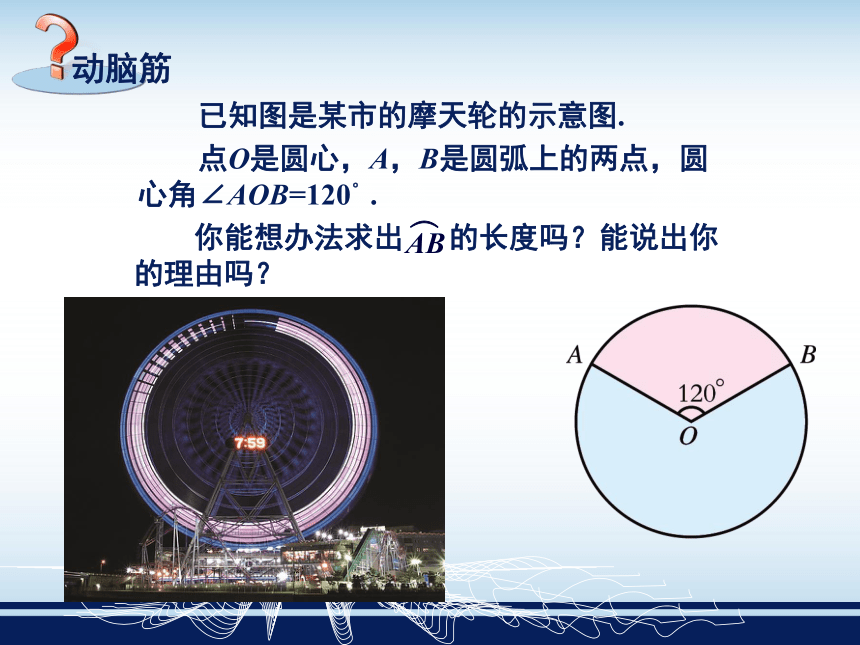
课件20张PPT。弧长和扇形的面积,圆锥的侧面展开图2.6——弧长和扇形的面积 在同一个圆中,如果圆心角相等,那么它们所对的弧相等吗? 这是根据圆的什么对称性得出的结论?相等.根据圆的旋转对称性. 已知图是某市的摩天轮的示意图. 点O是圆心,A,B是圆弧上的两点,圆心角∠AOB=120°. 你能想办法求出 的长度吗?能说出你的理由吗? 若线段OA的长r=15m,则 的长度l为多少? 我们知道圆周长的计算公式为C=2πr,其中r是圆的半径. 又由圆的性质可知,在同一个圆中,如果圆心角相等,那么它们所对的弧相等. 而一个圆的圆心角为360°,因此:1°的圆心角所对的弧长为从而,n°的圆心角所对的弧长l为
l = n · .半径为r的圆中,n°的圆心角所对的弧长l为
对于“动脑筋”栏目中提出的问题,我们就可以根据上面的弧长公式计算出
的长度l为例1 已知圆O的半径为30cm,求40°的圆心
角所对的弧长(精确到0.1cm) 举
例下图是某一圆弧管道,对于这个图案.(1)作出圆弧管道的圆心;(2)分别量出圆弧管道的外半径和内半径;(3)量出圆弧管道所对的圆心角的度数;(4)分别求出内外两个圆弧的弧长.答案:2.4cm,1.8cm.答案:155°答案:4.87cm,6.49cm. 图3-57是一个闹钟正面的内、外轮廓线. 内轮廓线由一段圆弧和一条弦AB组成,圆心为O,半径为3.2cm,圆心角∠AOB=83°,
求内轮廓线的圆弧的长度.答:
(此处是求优弧的长而非劣弧的长) 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形. 如图3-58,阴影部分是一个扇形,记做扇形OAB.如何求扇形的面积?1. 设圆O的半径为r,你能求出圆心角为1°的
扇形的面积吗?由于圆是旋转对称图形,因此圆心角为1°的扇形能够互相重合,从而圆心角为1°的扇形的面积等于圆面积的 ,
即
πr2.2. 从第1题的结论可以得出,在半径为r的
圆中,圆心角为n°的扇形的面积是
n · πr2. 半径为r的圆中,圆心角为n°的扇形的面积S为
其中l是n°的圆心角所对的弧长.例2 如图3-58,圆O的半径为1.5cm,圆心角
∠AOB=58°,求扇形OAB的面积(精确
到0.1cm2).举
例解 因为r=1.5cm,n=58,所以扇形OAB的面积为图3-59 如图3-59,在圆O中,∠AOB=120°,弦AB的长为2.6cm,求扇形OAB的面积(精确到0.1cm2).答:作OM⊥AB, 设 OA=r.图3-59r2=1.32+( r)2r≈1.50例1 如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度. ∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴OECD为矩形,∠EOD=90°,OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△BDO.∴ , ∴ ,∴r =12,∴ 的长度=结 束
l = n · .半径为r的圆中,n°的圆心角所对的弧长l为
对于“动脑筋”栏目中提出的问题,我们就可以根据上面的弧长公式计算出
的长度l为例1 已知圆O的半径为30cm,求40°的圆心
角所对的弧长(精确到0.1cm) 举
例下图是某一圆弧管道,对于这个图案.(1)作出圆弧管道的圆心;(2)分别量出圆弧管道的外半径和内半径;(3)量出圆弧管道所对的圆心角的度数;(4)分别求出内外两个圆弧的弧长.答案:2.4cm,1.8cm.答案:155°答案:4.87cm,6.49cm. 图3-57是一个闹钟正面的内、外轮廓线. 内轮廓线由一段圆弧和一条弦AB组成,圆心为O,半径为3.2cm,圆心角∠AOB=83°,
求内轮廓线的圆弧的长度.答:
(此处是求优弧的长而非劣弧的长) 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形. 如图3-58,阴影部分是一个扇形,记做扇形OAB.如何求扇形的面积?1. 设圆O的半径为r,你能求出圆心角为1°的
扇形的面积吗?由于圆是旋转对称图形,因此圆心角为1°的扇形能够互相重合,从而圆心角为1°的扇形的面积等于圆面积的 ,
即
πr2.2. 从第1题的结论可以得出,在半径为r的
圆中,圆心角为n°的扇形的面积是
n · πr2. 半径为r的圆中,圆心角为n°的扇形的面积S为
其中l是n°的圆心角所对的弧长.例2 如图3-58,圆O的半径为1.5cm,圆心角
∠AOB=58°,求扇形OAB的面积(精确
到0.1cm2).举
例解 因为r=1.5cm,n=58,所以扇形OAB的面积为图3-59 如图3-59,在圆O中,∠AOB=120°,弦AB的长为2.6cm,求扇形OAB的面积(精确到0.1cm2).答:作OM⊥AB, 设 OA=r.图3-59r2=1.32+( r)2r≈1.50例1 如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度. ∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴OECD为矩形,∠EOD=90°,OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△BDO.∴ , ∴ ,∴r =12,∴ 的长度=结 束
