2.6 弧长与扇形面积 课件 (5)(28PPT)
文档属性
| 名称 | 2.6 弧长与扇形面积 课件 (5)(28PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览




文档简介
课件28张PPT。2.6 弧长与扇形面积第二章 圆(1)已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?(2)什么叫圆心角?C=2πR,S⊙O=πR2
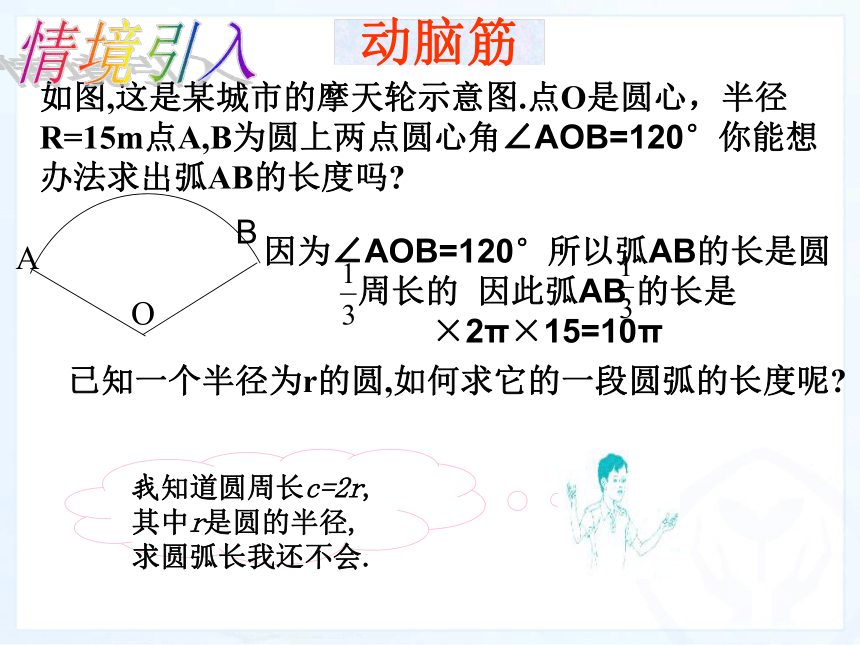
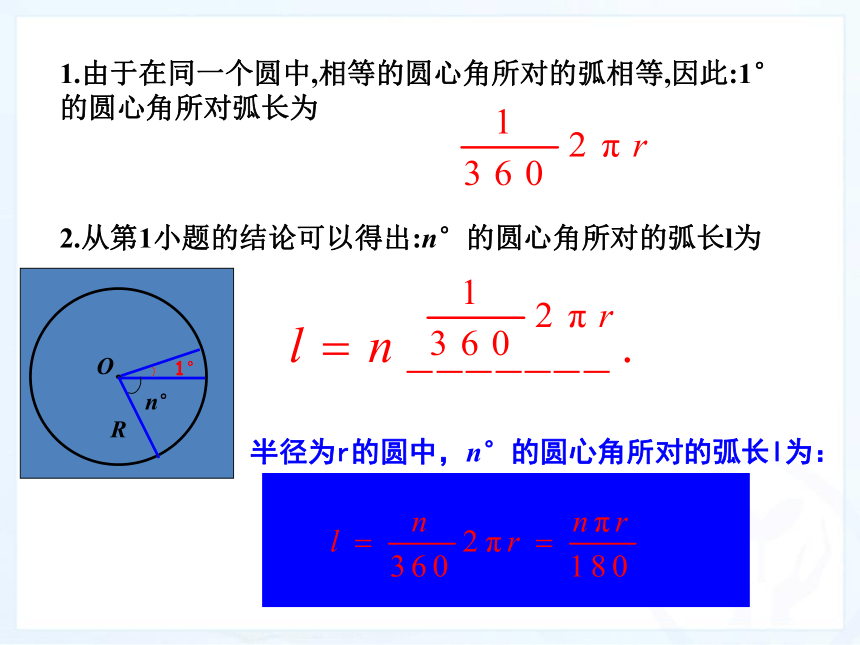
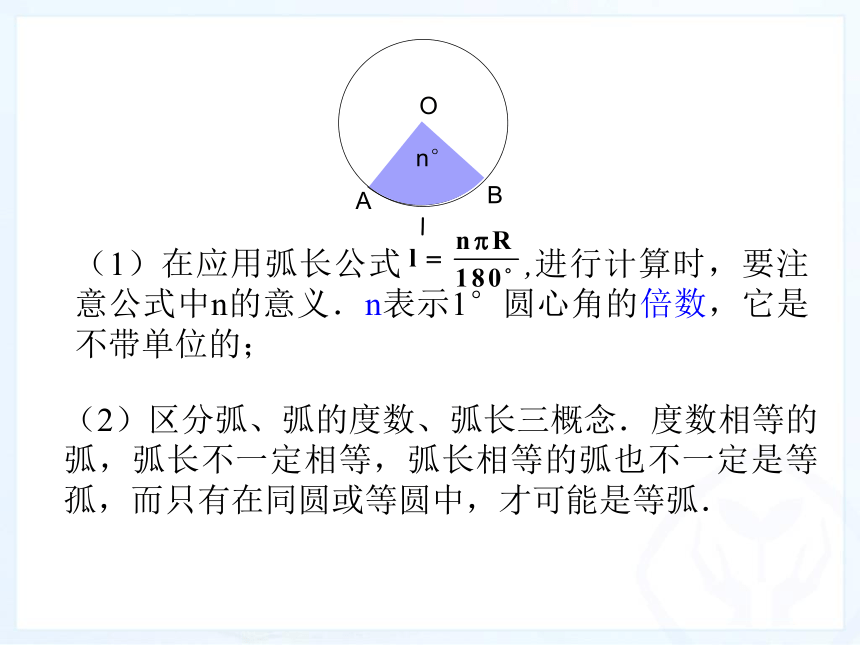
顶点在圆心,两边和圆相交所组成的角叫做圆心角知识回顾如图,这是某城市的摩天轮示意图.点O是圆心,半径R=15m点A,B为圆上两点圆心角∠AOB=120°你能想办法求出弧AB的长度吗?已知一个半径为r的圆,如何求它的一段圆弧的长度呢?我知道圆周长c=2r,其中r是圆的半径,求圆弧长我还不会.动脑筋AO因为∠AOB=120°所以弧AB的长是圆周长的 因此弧AB 的长是 ×2π×15=10πB情境引入1.由于在同一个圆中,相等的圆心角所对的弧相等,因此:1°的圆心角所对弧长为2.从第1小题的结论可以得出:n°的圆心角所对的弧长l为半径为r的圆中,n°的圆心角所对的弧长l为:1、弧长与哪些因素有关?2、在3个量l、R、n中,只要已知其中两个量就可以求第三个量,那么请将公式变形求出R和n。(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.(1)在应用弧长公式 ,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;已知圆O的半径为30cm,求40°的圆心角所对的弧长
(精确到0.1cm)
解:例140°的圆心角所对的弧长20.9cm开心练一练:
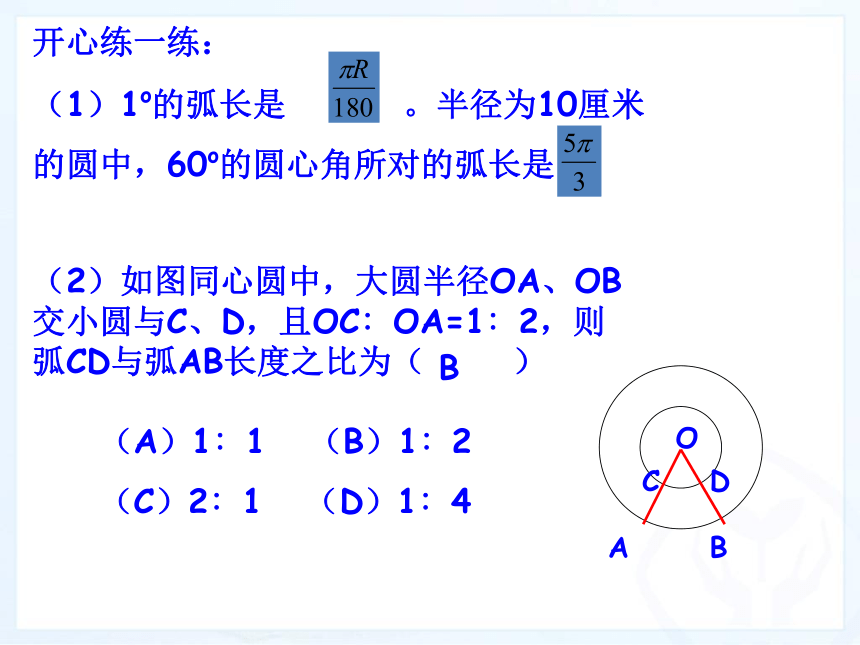
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )OABCD(A)1∶1 (B)1∶2
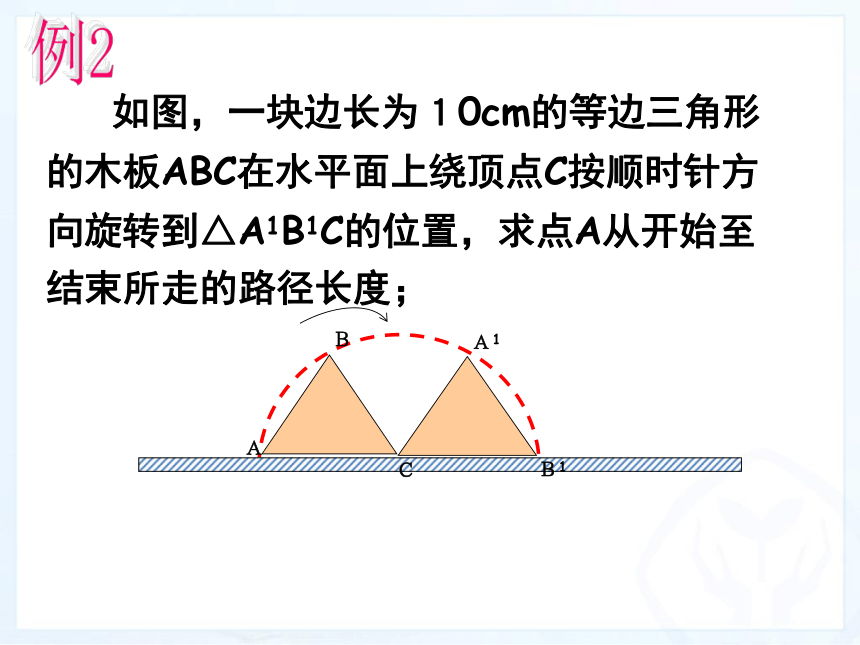
(C)2∶1 (D)1∶4B 如图,一块边长为10cm的等边三角形的木板ABC在水平面上绕顶点C按顺时针方向旋转到△A1B1C的位置,求点A从开始至结束所走的路径长度;ABCA1B1例21.已知弧所对的圆心角为900,半径是4,则弧长为 。
2. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 。
3、已知一条弧的弧长为4π ,那么这条弧所对的圆周角为450 ,这条弧所在的半径 。
4. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 2π1600B8什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。OBA圆心角如 何 求 扇 形 的 面 积 ?设 问 :扇形面积的大小到底和哪些因素有关呢?想 一 想 :1. 圆心角是3600的扇形面积是多少?2. 圆心角是1800的扇形面积是多少?3. 圆心角是900的扇形面积是多少?4. 圆心角是2700的扇形面积是多少? 结 论 :(当圆半径一定时)扇形的面积随着圆心角的增大而增大。扇形的周长是
2R+L S弧长公式与扇形的面积公式之间的联系:(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
例3:已知扇形AOB的半径1.5cm,∠AOB=58o,求扇形OAB的面积(结果精确到0.1cm2)3.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(精确到0.01cm)ABDCE弓形的面积 = S扇+ S△1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=____.
2、已知半径为2的扇形,面积为_____,则它的圆心角的度数为_____.
随堂练习例4.这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中OA=20cm,OC长为12cm,弧CD长为9πcm,求贴纸部分的面积 D解:设∠AOB=n°∵OC长为12cm,弧CD长为9πcm∴ 9π= ×12 解得n=135°即圆心角∠COD=135°S扇形AOB=S扇形COD=S扇面ACDB=S扇形AOB-S扇形COD=150π-54π=96πcm2答:贴纸部分的面积为96πcm2
拓展提高:如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 。如图,半圆的直径AB=2,弦CD∥AB,连AC.AD,∠CAD=30o,求阴影部分的面积。略解:连接OC.OD分析:所求阴影部分是非常规
图形,可转化为常规图形来解决.∠COD=60o如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0, ),OC与⊙D相交于点C,∠OCA=30°,求图中阴影部分的面积如图,Rt△ABC中,∠ABC=90°,AB=BC=2,以BC为直径的圆交AC于点D, 则图中阴影部分的面积为______ 1、正方形的边长为a,求阴影部分的面积随堂练习2、正方形的边长为a,求阴影部分的面积
3.等边三角形的边长为a,求阴影部分的面积
4.已知:下图中等腰直角三角形ABC的直角边长均为2,求三个图中的阴影部分的面积。 1.知识点:弧长、扇形面积的计算公式2、不规则图形的面积的求法:用规则的图形的面积来表示; 3、数学思想转化的应用:
①转化思想;②整体思想。知识梳理 5.已知:直角扇形OAB的半径为2,以OA为直径为半圆和以OB为直径的圆相交于M、N两部分,则扇形OAB的面积为 ,半圆的面积为 ,M与N的面积哪个大? 如果说学习上有捷径,那也一定是勤奋。
结束语
顶点在圆心,两边和圆相交所组成的角叫做圆心角知识回顾如图,这是某城市的摩天轮示意图.点O是圆心,半径R=15m点A,B为圆上两点圆心角∠AOB=120°你能想办法求出弧AB的长度吗?已知一个半径为r的圆,如何求它的一段圆弧的长度呢?我知道圆周长c=2r,其中r是圆的半径,求圆弧长我还不会.动脑筋AO因为∠AOB=120°所以弧AB的长是圆周长的 因此弧AB 的长是 ×2π×15=10πB情境引入1.由于在同一个圆中,相等的圆心角所对的弧相等,因此:1°的圆心角所对弧长为2.从第1小题的结论可以得出:n°的圆心角所对的弧长l为半径为r的圆中,n°的圆心角所对的弧长l为:1、弧长与哪些因素有关?2、在3个量l、R、n中,只要已知其中两个量就可以求第三个量,那么请将公式变形求出R和n。(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.(1)在应用弧长公式 ,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;已知圆O的半径为30cm,求40°的圆心角所对的弧长
(精确到0.1cm)
解:例140°的圆心角所对的弧长20.9cm开心练一练:
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )OABCD(A)1∶1 (B)1∶2
(C)2∶1 (D)1∶4B 如图,一块边长为10cm的等边三角形的木板ABC在水平面上绕顶点C按顺时针方向旋转到△A1B1C的位置,求点A从开始至结束所走的路径长度;ABCA1B1例21.已知弧所对的圆心角为900,半径是4,则弧长为 。
2. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 。
3、已知一条弧的弧长为4π ,那么这条弧所对的圆周角为450 ,这条弧所在的半径 。
4. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 2π1600B8什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。OBA圆心角如 何 求 扇 形 的 面 积 ?设 问 :扇形面积的大小到底和哪些因素有关呢?想 一 想 :1. 圆心角是3600的扇形面积是多少?2. 圆心角是1800的扇形面积是多少?3. 圆心角是900的扇形面积是多少?4. 圆心角是2700的扇形面积是多少? 结 论 :(当圆半径一定时)扇形的面积随着圆心角的增大而增大。扇形的周长是
2R+L S弧长公式与扇形的面积公式之间的联系:(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
例3:已知扇形AOB的半径1.5cm,∠AOB=58o,求扇形OAB的面积(结果精确到0.1cm2)3.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(精确到0.01cm)ABDCE弓形的面积 = S扇+ S△1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=____.
2、已知半径为2的扇形,面积为_____,则它的圆心角的度数为_____.
随堂练习例4.这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中OA=20cm,OC长为12cm,弧CD长为9πcm,求贴纸部分的面积 D解:设∠AOB=n°∵OC长为12cm,弧CD长为9πcm∴ 9π= ×12 解得n=135°即圆心角∠COD=135°S扇形AOB=S扇形COD=S扇面ACDB=S扇形AOB-S扇形COD=150π-54π=96πcm2答:贴纸部分的面积为96πcm2
拓展提高:如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 。如图,半圆的直径AB=2,弦CD∥AB,连AC.AD,∠CAD=30o,求阴影部分的面积。略解:连接OC.OD分析:所求阴影部分是非常规
图形,可转化为常规图形来解决.∠COD=60o如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0, ),OC与⊙D相交于点C,∠OCA=30°,求图中阴影部分的面积如图,Rt△ABC中,∠ABC=90°,AB=BC=2,以BC为直径的圆交AC于点D, 则图中阴影部分的面积为______ 1、正方形的边长为a,求阴影部分的面积随堂练习2、正方形的边长为a,求阴影部分的面积
3.等边三角形的边长为a,求阴影部分的面积
4.已知:下图中等腰直角三角形ABC的直角边长均为2,求三个图中的阴影部分的面积。 1.知识点:弧长、扇形面积的计算公式2、不规则图形的面积的求法:用规则的图形的面积来表示; 3、数学思想转化的应用:
①转化思想;②整体思想。知识梳理 5.已知:直角扇形OAB的半径为2,以OA为直径为半圆和以OB为直径的圆相交于M、N两部分,则扇形OAB的面积为 ,半圆的面积为 ,M与N的面积哪个大? 如果说学习上有捷径,那也一定是勤奋。
结束语
