2.6 弧长与扇形面积 课件 (6)(18PPT)
文档属性
| 名称 | 2.6 弧长与扇形面积 课件 (6)(18PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览





文档简介
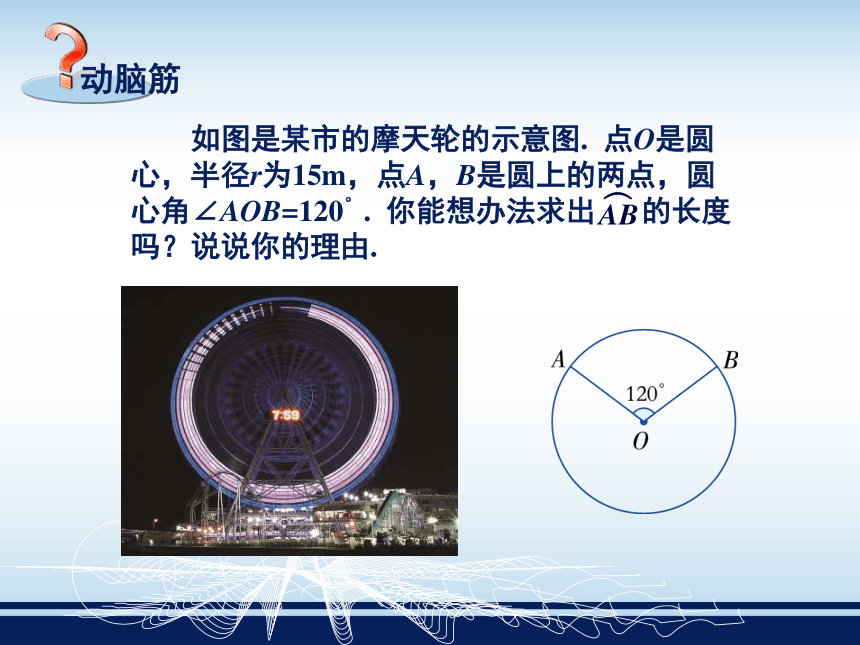
课件18张PPT。弧长与扇形面积(一)2.6 如图是某市的摩天轮的示意图. 点O是圆
心,半径r为15m,点A,B是圆上的两点,圆
心角∠AOB=120°. 你能想办法求出 的长度
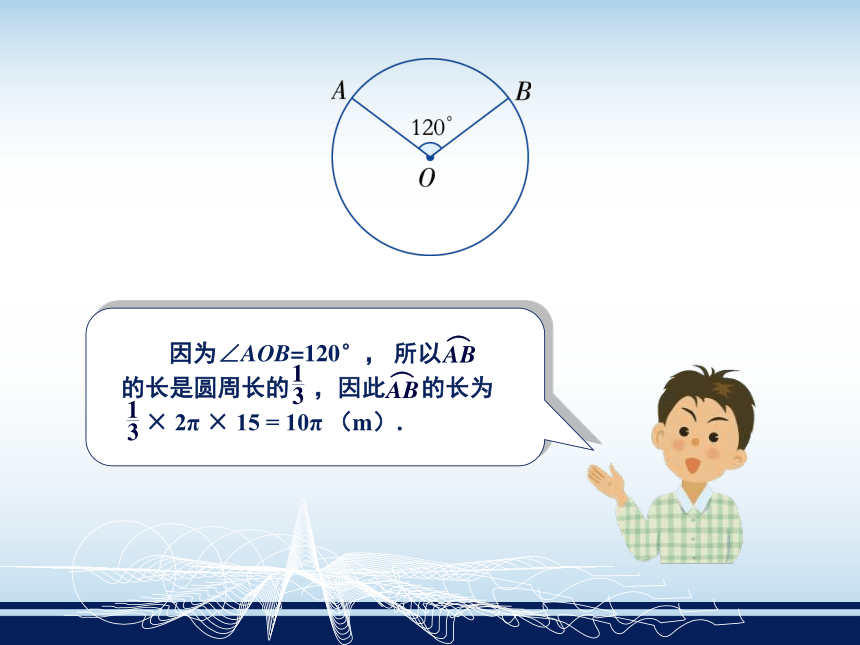
吗?说说你的理由. 我们知道圆周长的计算公式为C=2πr,
其中r是圆的半径,即360°的圆心角所对
的弧长就是圆周长C.如果∠AOB=n°,你能求出 的长吗? 又由圆的性质可知,在同一个圆中,如果圆心角相等,那么它们所对的弧相等. 而一个圆的圆心角为360°,因此:1°的圆心角所对的弧长为从而,n°的圆心角所对的弧长l为
l = n · .半径为r的圆中,n°的圆心角所对的弧长l为
由此得出以下结论:例1 已知圆O的半径为30cm,求40°的圆心
角所对的弧长(精确到0.1cm) 举
例如图所示,一个边长为10cm的等边三角形木板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A′B′C的位置,求顶点A从开始到结束所经过的路程为多少.举
例例2 解 由图可知,由于∠A′CB′ =60°,则等边
三角形木板绕点C按顺时针方向旋转了120°,
即∠ACA′ =120°,这说明顶点A经过的
路程长等于 的长. ∵ 等边三角形ABC的边长为10cm,∴ 所在圆的半径为10cm. ∴答:顶点A从开始到结束时所经过的
路程为 cm. 如图是一个闹钟正面的内、外轮廓线. 内
轮廓线由一段圆弧和一条弦AB组成,圆心
为O,半径为3.2cm,圆心角∠AOB=83°,
求内轮廓线的圆弧的长度.1.例 如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度. 连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴四边形OECD为矩形,
∠EOD=90°, OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△ODB.∴ , ∴ ,∴ r =12,∴ 的长度=课堂小结:这节课我们学习了什么?弧长公式:半径为r的圆中,n°的圆心角所对的弧长l为
作业:课本81页第1题结 束
心,半径r为15m,点A,B是圆上的两点,圆
心角∠AOB=120°. 你能想办法求出 的长度
吗?说说你的理由. 我们知道圆周长的计算公式为C=2πr,
其中r是圆的半径,即360°的圆心角所对
的弧长就是圆周长C.如果∠AOB=n°,你能求出 的长吗? 又由圆的性质可知,在同一个圆中,如果圆心角相等,那么它们所对的弧相等. 而一个圆的圆心角为360°,因此:1°的圆心角所对的弧长为从而,n°的圆心角所对的弧长l为
l = n · .半径为r的圆中,n°的圆心角所对的弧长l为
由此得出以下结论:例1 已知圆O的半径为30cm,求40°的圆心
角所对的弧长(精确到0.1cm) 举
例如图所示,一个边长为10cm的等边三角形木板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A′B′C的位置,求顶点A从开始到结束所经过的路程为多少.举
例例2 解 由图可知,由于∠A′CB′ =60°,则等边
三角形木板绕点C按顺时针方向旋转了120°,
即∠ACA′ =120°,这说明顶点A经过的
路程长等于 的长. ∵ 等边三角形ABC的边长为10cm,∴ 所在圆的半径为10cm. ∴答:顶点A从开始到结束时所经过的
路程为 cm. 如图是一个闹钟正面的内、外轮廓线. 内
轮廓线由一段圆弧和一条弦AB组成,圆心
为O,半径为3.2cm,圆心角∠AOB=83°,
求内轮廓线的圆弧的长度.1.例 如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度. 连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴四边形OECD为矩形,
∠EOD=90°, OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△ODB.∴ , ∴ ,∴ r =12,∴ 的长度=课堂小结:这节课我们学习了什么?弧长公式:半径为r的圆中,n°的圆心角所对的弧长l为
作业:课本81页第1题结 束
