2.7正多边形与圆 课件 (1)(14PPT)
文档属性
| 名称 | 2.7正多边形与圆 课件 (1)(14PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览


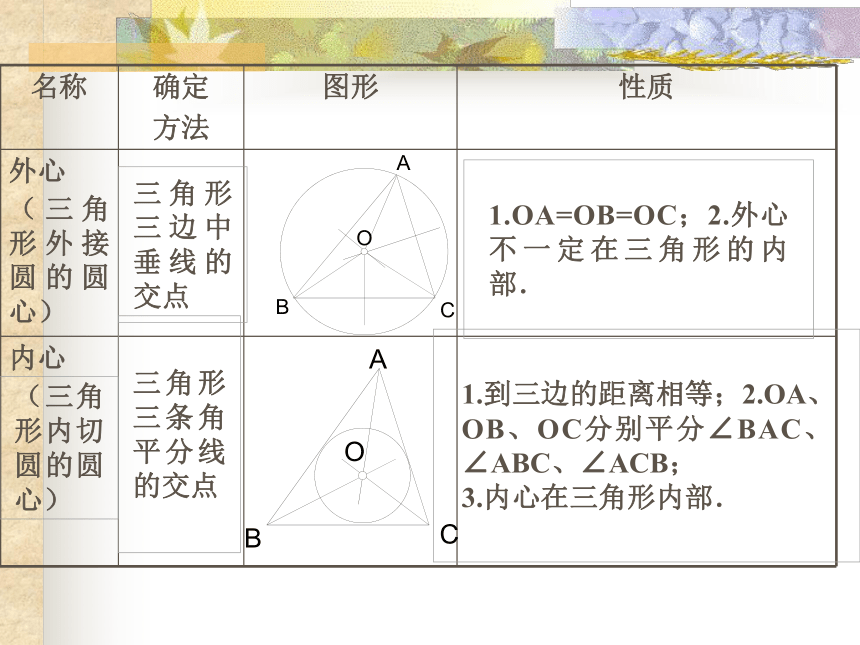
文档简介
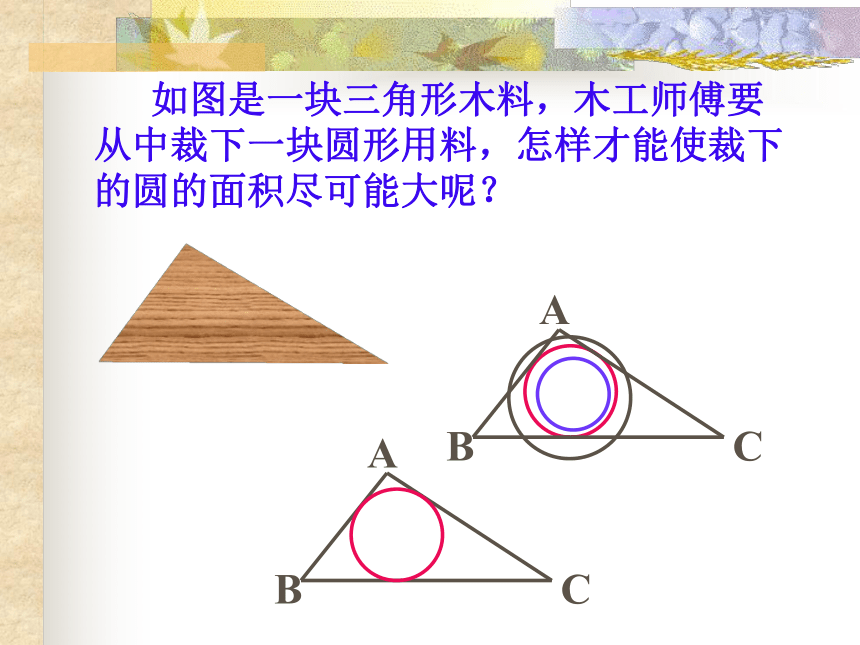
课件14张PPT。三角形的内切圆议一议:
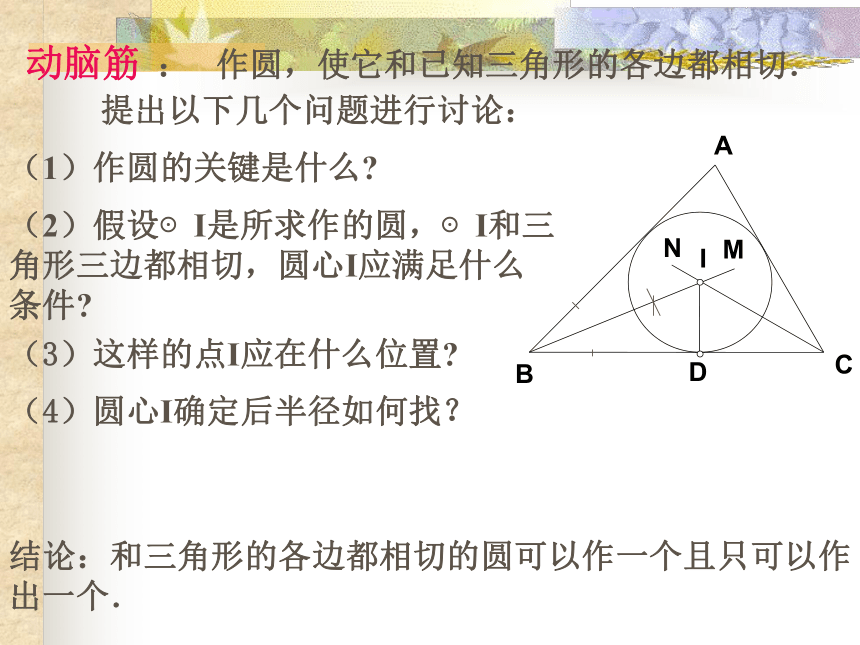
想在三角形硬板上剪下一个面积最大的圆形纸板,应当怎样剪? 动脑筋 : 作圆,使它和已知三角形的各边都相切.(1)作圆的关键是什么? 提出以下几个问题进行讨论:(2)假设⊙I是所求作的圆,⊙I和三
角形三边都相切,圆心I应满足什么
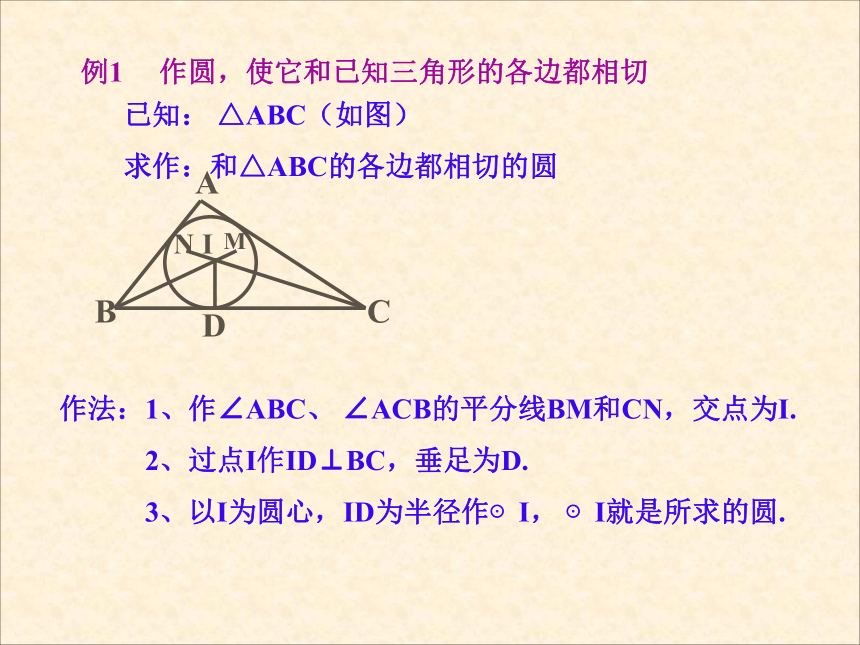
条件?(3)这样的点I应在什么位置? (4)圆心I确定后半径如何找?结论:和三角形的各边都相切的圆可以作一个且只可以作出一个.ABCIMND例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆. 回顾与小结:
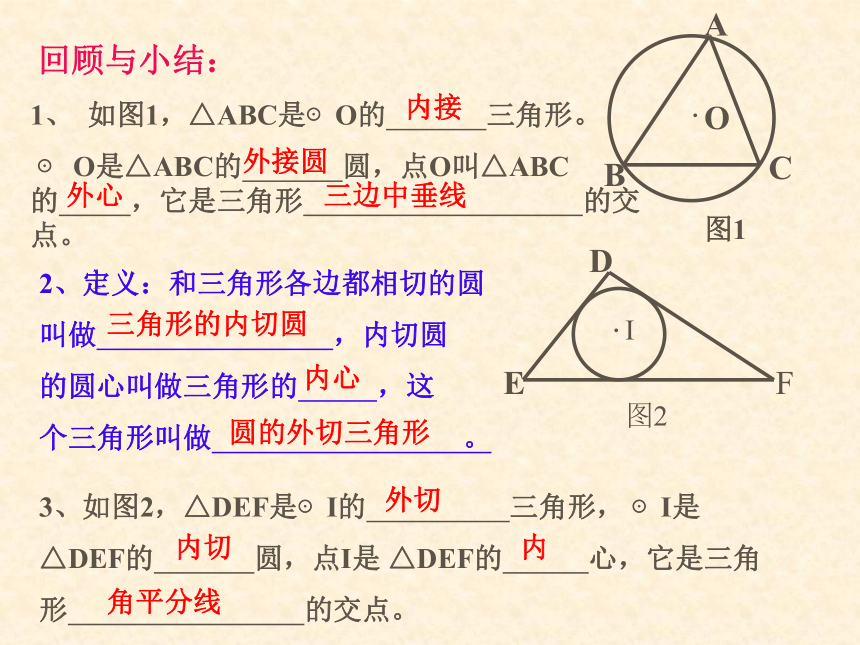
1、 如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形 的交点。13、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。2、定义:和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。三角形的内切圆内心圆的外切三角形外切内切内角平分线内接外接圆外心三边中垂线三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上; 1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:(三角形外接圆的圆心)巩固练习:
判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆(错)
错错对对 对总结:
定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆圆的外切多边形内切外切如上图,四边形DEFG是⊙O的 四
边形,⊙O是四边形DEFG的 圆,
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
13020(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
练习:
填空:如图, △ABC的顶点在⊙O上, △ABC的各边与
⊙I都相切,则△ABC是⊙I的 三角形;
△ABC是⊙O的 三角形; ⊙I叫△ABC的 圆;
⊙O叫△ABC的 圆,点I是△ABC的 心,点O是
△ABC的 心
I外切内接内切外接..O内外 课堂小结:
1、本节课从实际问题入手,探索得出三角形内切圆的作法 .
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,并介绍了多边形的
内切圆、圆的外切多边形的概念。
3、学习 时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4、利用三角形内心的性质解题时,要注意整体思想的运
用,在解决实际问题时,要注意把实际问题转化为数学问题。
谢谢, 再见 !
想在三角形硬板上剪下一个面积最大的圆形纸板,应当怎样剪? 动脑筋 : 作圆,使它和已知三角形的各边都相切.(1)作圆的关键是什么? 提出以下几个问题进行讨论:(2)假设⊙I是所求作的圆,⊙I和三
角形三边都相切,圆心I应满足什么
条件?(3)这样的点I应在什么位置? (4)圆心I确定后半径如何找?结论:和三角形的各边都相切的圆可以作一个且只可以作出一个.ABCIMND例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆. 回顾与小结:
1、 如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形 的交点。13、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。2、定义:和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。三角形的内切圆内心圆的外切三角形外切内切内角平分线内接外接圆外心三边中垂线三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上; 1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:(三角形外接圆的圆心)巩固练习:
判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆(错)
错错对对 对总结:
定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆圆的外切多边形内切外切如上图,四边形DEFG是⊙O的 四
边形,⊙O是四边形DEFG的 圆,
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
13020(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
练习:
填空:如图, △ABC的顶点在⊙O上, △ABC的各边与
⊙I都相切,则△ABC是⊙I的 三角形;
△ABC是⊙O的 三角形; ⊙I叫△ABC的 圆;
⊙O叫△ABC的 圆,点I是△ABC的 心,点O是
△ABC的 心
I外切内接内切外接..O内外 课堂小结:
1、本节课从实际问题入手,探索得出三角形内切圆的作法 .
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,并介绍了多边形的
内切圆、圆的外切多边形的概念。
3、学习 时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4、利用三角形内心的性质解题时,要注意整体思想的运
用,在解决实际问题时,要注意把实际问题转化为数学问题。
谢谢, 再见 !
