第二十八章锐角三角函数同步强化练习(含解析)
文档属性
| 名称 | 第二十八章锐角三角函数同步强化练习(含解析) | 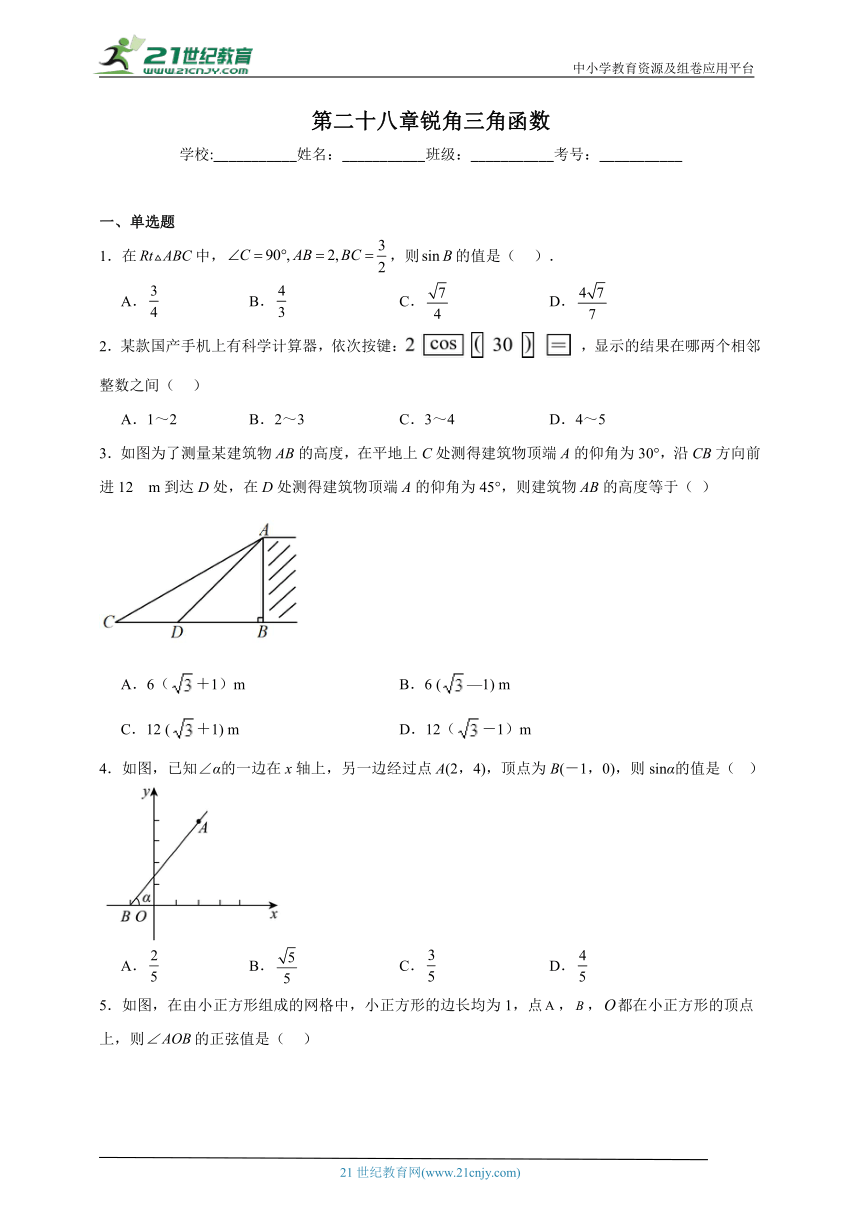 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:35:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十八章锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,则的值是( ).
A. B. C. D.
2.某款国产手机上有科学计算器,依次按键: ,显示的结果在哪两个相邻整数之间( )
A.1~2 B.2~3 C.3~4 D.4~5
3.如图为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12 m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A.6(+1)m B.6 (—1) m
C.12 (+1) m D.12(-1)m
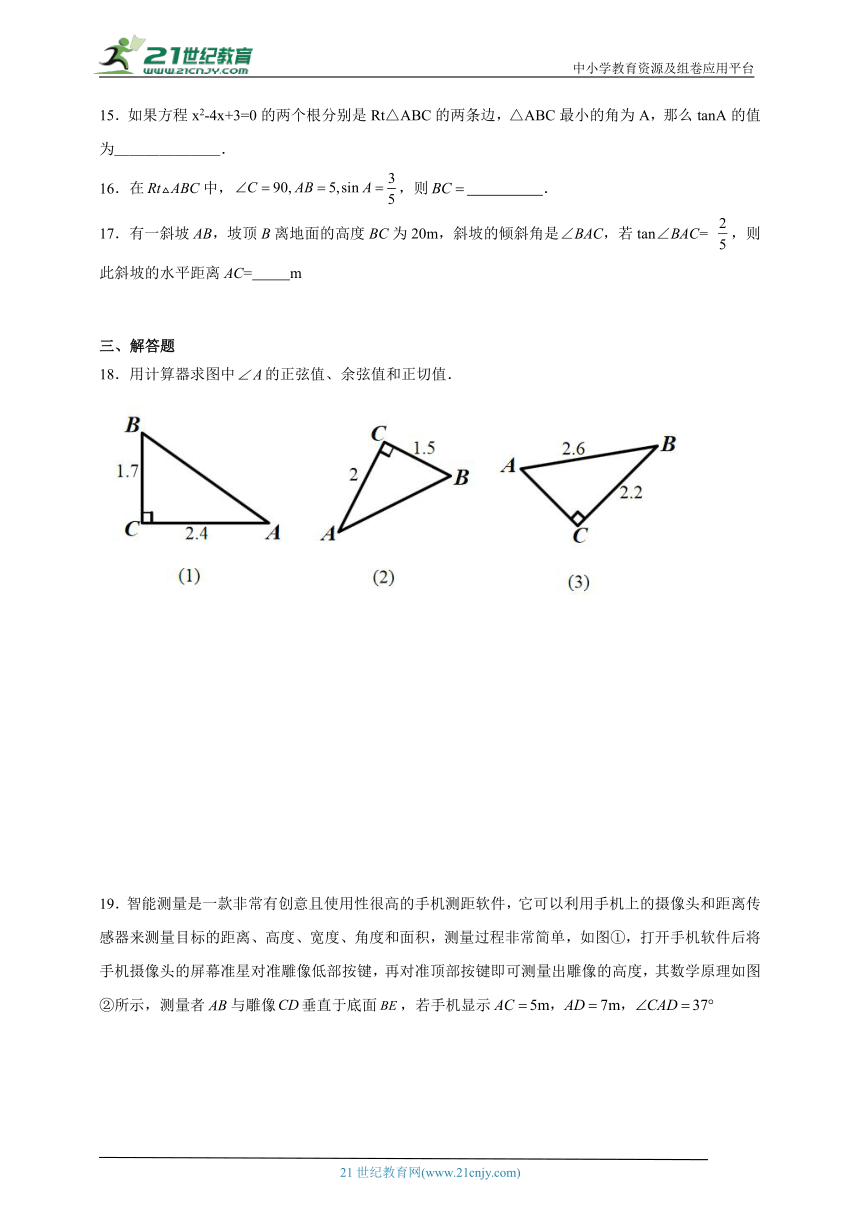
4.如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为B(-1,0),则sinα的值是( )
A. B. C. D.
5.如图,在由小正方形组成的网格中,小正方形的边长均为1,点,,都在小正方形的顶点上,则的正弦值是( )
A. B. C. D.
6.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口,4小时后货船在小岛的正东方向,则货船的航行速度是( )
A.7海里/时 B.7海里/时 C.7海里/时 D.28海里/时
7.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
8.如图,小明想测量斜坡旁一棵垂直于地面的树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,斜坡顶点到地面的垂直高度,则树的高度是( )
A.20 B.30 C.30 D.40
9.sin30°的值为( )
A. B. C. D.
10.如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示出的值,正确的是( )
A. B. C. D.
11.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.100米
12.如图,在等腰中,,,是上一点,若,则的长为( ).
A.2 B. C. D.1
二、填空题
13.如图,已知在中,,将绕点B顺时针旋转,点分别落在点处,联结,如果,那么边的长 .
14.用计算器求的值,按键顺序是 .
15.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为_______.
16.在中,,则 .
17.有一斜坡AB,坡顶B离地面的高度BC为20m,斜坡的倾斜角是∠BAC,若tan∠BAC= ,则此斜坡的水平距离AC= m
三、解答题
18.用计算器求图中的正弦值、余弦值和正切值.
19.智能测量是一款非常有创意且使用性很高的手机测距软件,它可以利用手机上的摄像头和距离传感器来测量目标的距离、高度、宽度、角度和面积,测量过程非常简单,如图①,打开手机软件后将手机摄像头的屏幕准星对准雕像低部按键,再对准顶部按键即可测量出雕像的高度,其数学原理如图②所示,测量者与雕像垂直于底面,若手机显示
(1)求雕像的高度;
(2)求测量者离雕像底部的距离的长.
(结果保留1位小数,参考数据,)
20.已知:如图,是的直径,弦于点E,G是弧上一动点且不与点A,C重合,的延长线交于点F,连结.,.
(1)求半径长.
(2)求扇形的面积.
21.在直角三角形ABC中,∠C=90°,,∠B的平分线BD交AC于D,BD=16.求AB的长.
22.如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=,求tan∠FBE的值.
23.某阶梯的形状如图所示,其中线段,部分的坡角为,部分的坡角为,.如果每个台阶的高不超过,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足时,按一个台阶计算)
24.如图(1)(2),图(1)是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图(2).
已知铁环的半径为5个单位(每个单位为),设铁环中心为D,铁环钩与铁环相切点为M,铁环与地面接触点为A,,且.
(1)求点M离地面的高度 (单位:厘米);
(2)设人站立点C与点A的水平距离等于11个单位,求铁环钩的长度(单位:厘米).
《第二十八章锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D B A B C A B
题号 11 12
答案 D A
1.C
【分析】首先根据勾股定理求得AC的长,然后根据正弦的定义即可求解.
【详解】解:根据勾股定理可得:AC==,
∴sinB==.
故选:C.
【点睛】本题主要考查了求一个角的正弦值,求出AC的长,正确理解正弦的定义是解题关键.
2.A
【分析】用计算器计算得得出答案.
【详解】解:使用计算器计算得,
,
∴显示的结果在1~2之间.
故选:A.
【点睛】本题考查计算器的使用,正确地操作和计算是得出正确答案的前提.
3.A
【详解】根据题意可得:BC=
∴AB=6(+1).
故选A.
4.D
【详解】如图:过点A作垂线AC⊥x轴于点C.
则AC=4,BC=3,故由勾股定理得AB=5.
sinB==.故选D.
5.B
【分析】过点作于点.先利用勾股定理求出、的长,再利用的面积求出的长,最后在直角中求出的正弦值.本题考查了解直角三角形,构造直角三角形,利用的面积求出边上的高是解决本题的关键.
【详解】解:过点作于点.
,
.
,
.
.
.
故选:B.
6.A
【详解】试题解析:设货船的航行速度为海里/时,小时后货船在点处,作于点.
由题意海里,海里,
在中,
所以
在中,
所以
所以
解得:
故选A.
7.B
【详解】∵α是锐角,
∴cosα>0,
∵cosα<,
∴0又∵cos90°=0,cos45°=,
∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα<,
∴0又∵tan0°=0,tan60°=,
0<α<60°;
故45°<α<60°.
故选B.
【点睛】本题主要考查了余弦函数、正切函数的增减性与特殊角的余弦函数、正切函数值,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键
8.C
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
【详解】在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=(m),
∴AB=BC sin60°=20×=30(m).
故选C.
【点睛】此题考查了解直角三角形的应用-仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.
9.A
【分析】直接利用特殊角的三角函数值写出答案即可.
【详解】解:sin30°=,
故选:A.
【点睛】本题考查特殊角的三角函数值.熟记特殊角的三角函数值是解决此题的关键.
10.B
【分析】由同角的余角相等可得,在三个直角三角形中由正弦函数的定义即可确定答案.
【详解】,,
,
,
;
故正确的是B选项;
故选:B.
【点睛】本题考查了正弦函数的定义,同角的余角相等,掌握正弦函数的定义是关键.
11.D
【分析】在热气球C处测得地面B点的俯角分别为45°,BD=CD=100米,再在Rt△ACD中求出AD的长,据此即可求出AB的长.
【详解】∵在热气球C处测得地面B点的俯角分别为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角分别为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选D.
【点睛】本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
12.A
【详解】如图,作DE⊥AB于E.
∵tan∠DBA= = ,
∴BE=5DE.
∵△ABC为等腰直角三角形,
∴∠A=45°,
∴AE=DE.
∴BE=5AE,
又∵AC=6,
∴AB=6 ,
∴AE+BE=AE+5AE=6 ,
∴AE= ,
∴在等腰直角△ADE中,
由勾股定理,得AE=,AD=2.
故选:A.
【点睛】本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解.
13.
【分析】由旋转变换易证,,,,由,得;设,由三角函数得,;在中,运用勾股定理求解得,所以.
【详解】如图,由旋转知,,,,为等边三角形,
∴, ,,
∴,
∵
∴
设,则,
中,
∴,解得(负值舍去),
故答案为:
【点睛】本题主要考查旋转变换、全等三角形的性质、等边三角形的性质、勾股定理及特殊角三角函数;能够灵活运用相关知识导出线段间的数量关系是解题的关键.
14.MODE,tan,35,=.
【分析】根据计算器中对应的已知一个角的正切值求这个角的算法求解即可.
【详解】解:先按MODE,选择模式;再键tan,35,最后按=;可得到这个角的函数值.
故答案为:MODE,tan,35,=
【点睛】本题考查计算器—三角函数,要求同学们能熟练应用计算器,会用计算器进行计算.
15.或
【详解】解方程x2-4x+3=0得,x1=1,x2=3,
①当3是直角边时,∵△ABC最小的角为A,∴tanA=;
②当3是斜边时,根据勾股定理,∠A的邻边=,∴tanA=;
所以tanA的值为或.
16.3
【分析】根据, ,,解直角三角形即可得到答案.
【详解】解:如图:在中,,
,,
,
故答案为:3.
【点睛】本题主要考查了解直角三角形,解题的关键在于能够熟练掌握相关知识进行求解.
17.50
【分析】根据正切三角函数计算求值即可.
【详解】解:由题意作图如下,
Rt△ABC中,∠C=90°,BC=20m,tan∠A=,
∴AC=BC÷tan∠A=20×=50m,
故答案为:50.
【点睛】本题考查了正切三角函数,掌握正切的概念是解题关键.
18.图(1),,;图(2),,;图(3),,
【分析】根据勾股定理求得另外一边的长度,在利用三角函数的定义求解即可.
【详解】解:由图(1)得,,
由勾股定理得:
,,
由图(2)得:,
由勾股定理得:
,,
由图(3)得:,
由勾股定理得:
,,
【点睛】此题考查了三角函数的定义,涉及了勾股定理,解题的关键是熟练掌握三角函数的有关定义.
19.(1)雕像的高度是
(2)测量者离雕像底部的距离为
【分析】(1)过点C作于F,在中,求出的长,在中,求出的长即可;
(2)过A作于G,求出,在中求出的长.
【详解】(1)过点C作于F
在中,
∴
在中,
答:雕像的高度是.
(2)过A作于G,则四边形为矩形
在中,由于
∴
在中,
∴
∴
答:测量者离雕像底部的距离为.
【点睛】本题考查了解直角三角形的应用仰角俯角问题,将解直角三角形与实际问题结合,需要构造合适的直角三角形.
20.(1)4
(2)
【分析】(1)连接.设的半径为R.在中,根据,构建方程即可解决问题;
(2)连接,根据可得,再由垂径定理可得,根据扇形的面积公式求解即可.
【详解】(1)解:如图,连接.设的半径为R.
∵,
∴,
在中,
∵,
∴,
解得.
(2)解:如图,连接,
∵,
∴,
∵,
∴
∴,
∴扇形的面积.
【点睛】本题考查的是特殊角的三角函数、圆周角定理的推论和垂径定理的应用,掌握圆周角定理的推论、垂径定理和勾股定理是解题的关键,学会添加常用辅助线.
21..
【分析】首先根据锐角三角形函数值的知识求出∠B的度数,进而求出BC的长度,在直角三角形中,利用30°的角所对的直角边等于斜边的一半求出AB的长.
【详解】在直角三角形ABC中,∠C=90°,
∵cosA=,
∴∠A=30°,
∴∠B=60°,
∵BD是∠B的平分线,
∴∠DBC=30°,
在直角三角形DBC中
cos30°=,
∴BC=16×=8,
在直角三角形ACB中,
∵∠A=30°,
∴30°的角所对的直角边等于斜边的一半,
∴AB=16.
【点睛】本题主要考查了解直角三角形的知识,解答本题的关键是掌握锐角三角形函数的定义以及含30°角直角三角形的性质,此题难度不大.
22.(1)证明见解析
(2)
【分析】(1)根据矩形的性质可知沿折叠为,得出,再根据三角形的内角和为180°,可知 得出 即可证明.
(2)已知 设 得出 由(1)中可得 .
【详解】(1)证明:∵四边形ABCD是矩形,
∴
∵△BCE沿BE折叠为△BFE,
,
又∵
∴∠ABF=∠DFE,
∴△ABF∽△DFE.
(2)在中,
∴设
∵沿折叠为,
又
.
【点睛】本题考查了矩形的性质,折叠的性质,三角形相似的判定和性质,正弦函数,正切函数,熟练掌握事件相似的相似和判定,灵活运用三角函数是解题的关键.
23.至少有13个台阶
【分析】根据含30度的直角三角形三边的关系和等腰直角三角形的性质得到BD和CE的长,即可解决问题.
【详解】解:∵AB部分的坡角为45°,AD=1.5m,
∴BD=AD=1.5m,
∴AB= m,
∵AB=BC,
∴BC= m,
∵BC部分的坡角为30°,
∴EC=BC=m,
∴BD+CE=(m),
∵每个台阶的高不超过20cm,
∴至少有台阶的数量为()×100÷20≈13.
【点睛】本题考查了坡度的概念:斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值,即斜坡的坡度等于斜坡的坡角的正弦.也考查了含30度的直角三角形三边的关系和等腰直角三角形的性质.
24.(1);(2)
【分析】本题考查了三角函数的应用、勾股定理:
(1)过M作平行的直线,与分别相交于,根据的三角函数得出和的长度,从而求出的长度;
(2)根据,,得出与的关系,然后根据的勾股定理得出的长度.
【详解】解:(1)过M作平行的直线,与分别相交于,
在中,,
所以(单位),
(单位)
所以铁环钩离地面的高度为;
(2)因为,,
所以,
即得,
在中,(单位),
由勾股定理,
即,
解得(单位),
即,
所以铁环钩的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十八章锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,则的值是( ).
A. B. C. D.
2.某款国产手机上有科学计算器,依次按键: ,显示的结果在哪两个相邻整数之间( )
A.1~2 B.2~3 C.3~4 D.4~5
3.如图为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12 m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A.6(+1)m B.6 (—1) m
C.12 (+1) m D.12(-1)m
4.如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为B(-1,0),则sinα的值是( )
A. B. C. D.
5.如图,在由小正方形组成的网格中,小正方形的边长均为1,点,,都在小正方形的顶点上,则的正弦值是( )
A. B. C. D.
6.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口,4小时后货船在小岛的正东方向,则货船的航行速度是( )
A.7海里/时 B.7海里/时 C.7海里/时 D.28海里/时
7.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
8.如图,小明想测量斜坡旁一棵垂直于地面的树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,斜坡顶点到地面的垂直高度,则树的高度是( )
A.20 B.30 C.30 D.40
9.sin30°的值为( )
A. B. C. D.
10.如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示出的值,正确的是( )
A. B. C. D.
11.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.100米
12.如图,在等腰中,,,是上一点,若,则的长为( ).
A.2 B. C. D.1
二、填空题
13.如图,已知在中,,将绕点B顺时针旋转,点分别落在点处,联结,如果,那么边的长 .
14.用计算器求的值,按键顺序是 .
15.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为_______.
16.在中,,则 .
17.有一斜坡AB,坡顶B离地面的高度BC为20m,斜坡的倾斜角是∠BAC,若tan∠BAC= ,则此斜坡的水平距离AC= m
三、解答题
18.用计算器求图中的正弦值、余弦值和正切值.
19.智能测量是一款非常有创意且使用性很高的手机测距软件,它可以利用手机上的摄像头和距离传感器来测量目标的距离、高度、宽度、角度和面积,测量过程非常简单,如图①,打开手机软件后将手机摄像头的屏幕准星对准雕像低部按键,再对准顶部按键即可测量出雕像的高度,其数学原理如图②所示,测量者与雕像垂直于底面,若手机显示
(1)求雕像的高度;
(2)求测量者离雕像底部的距离的长.
(结果保留1位小数,参考数据,)
20.已知:如图,是的直径,弦于点E,G是弧上一动点且不与点A,C重合,的延长线交于点F,连结.,.
(1)求半径长.
(2)求扇形的面积.
21.在直角三角形ABC中,∠C=90°,,∠B的平分线BD交AC于D,BD=16.求AB的长.
22.如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=,求tan∠FBE的值.
23.某阶梯的形状如图所示,其中线段,部分的坡角为,部分的坡角为,.如果每个台阶的高不超过,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足时,按一个台阶计算)
24.如图(1)(2),图(1)是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图(2).
已知铁环的半径为5个单位(每个单位为),设铁环中心为D,铁环钩与铁环相切点为M,铁环与地面接触点为A,,且.
(1)求点M离地面的高度 (单位:厘米);
(2)设人站立点C与点A的水平距离等于11个单位,求铁环钩的长度(单位:厘米).
《第二十八章锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D B A B C A B
题号 11 12
答案 D A
1.C
【分析】首先根据勾股定理求得AC的长,然后根据正弦的定义即可求解.
【详解】解:根据勾股定理可得:AC==,
∴sinB==.
故选:C.
【点睛】本题主要考查了求一个角的正弦值,求出AC的长,正确理解正弦的定义是解题关键.
2.A
【分析】用计算器计算得得出答案.
【详解】解:使用计算器计算得,
,
∴显示的结果在1~2之间.
故选:A.
【点睛】本题考查计算器的使用,正确地操作和计算是得出正确答案的前提.
3.A
【详解】根据题意可得:BC=
∴AB=6(+1).
故选A.
4.D
【详解】如图:过点A作垂线AC⊥x轴于点C.
则AC=4,BC=3,故由勾股定理得AB=5.
sinB==.故选D.
5.B
【分析】过点作于点.先利用勾股定理求出、的长,再利用的面积求出的长,最后在直角中求出的正弦值.本题考查了解直角三角形,构造直角三角形,利用的面积求出边上的高是解决本题的关键.
【详解】解:过点作于点.
,
.
,
.
.
.
故选:B.
6.A
【详解】试题解析:设货船的航行速度为海里/时,小时后货船在点处,作于点.
由题意海里,海里,
在中,
所以
在中,
所以
所以
解得:
故选A.
7.B
【详解】∵α是锐角,
∴cosα>0,
∵cosα<,
∴0
∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα<,
∴0
0<α<60°;
故45°<α<60°.
故选B.
【点睛】本题主要考查了余弦函数、正切函数的增减性与特殊角的余弦函数、正切函数值,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键
8.C
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
【详解】在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=(m),
∴AB=BC sin60°=20×=30(m).
故选C.
【点睛】此题考查了解直角三角形的应用-仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.
9.A
【分析】直接利用特殊角的三角函数值写出答案即可.
【详解】解:sin30°=,
故选:A.
【点睛】本题考查特殊角的三角函数值.熟记特殊角的三角函数值是解决此题的关键.
10.B
【分析】由同角的余角相等可得,在三个直角三角形中由正弦函数的定义即可确定答案.
【详解】,,
,
,
;
故正确的是B选项;
故选:B.
【点睛】本题考查了正弦函数的定义,同角的余角相等,掌握正弦函数的定义是关键.
11.D
【分析】在热气球C处测得地面B点的俯角分别为45°,BD=CD=100米,再在Rt△ACD中求出AD的长,据此即可求出AB的长.
【详解】∵在热气球C处测得地面B点的俯角分别为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角分别为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选D.
【点睛】本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
12.A
【详解】如图,作DE⊥AB于E.
∵tan∠DBA= = ,
∴BE=5DE.
∵△ABC为等腰直角三角形,
∴∠A=45°,
∴AE=DE.
∴BE=5AE,
又∵AC=6,
∴AB=6 ,
∴AE+BE=AE+5AE=6 ,
∴AE= ,
∴在等腰直角△ADE中,
由勾股定理,得AE=,AD=2.
故选:A.
【点睛】本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解.
13.
【分析】由旋转变换易证,,,,由,得;设,由三角函数得,;在中,运用勾股定理求解得,所以.
【详解】如图,由旋转知,,,,为等边三角形,
∴, ,,
∴,
∵
∴
设,则,
中,
∴,解得(负值舍去),
故答案为:
【点睛】本题主要考查旋转变换、全等三角形的性质、等边三角形的性质、勾股定理及特殊角三角函数;能够灵活运用相关知识导出线段间的数量关系是解题的关键.
14.MODE,tan,35,=.
【分析】根据计算器中对应的已知一个角的正切值求这个角的算法求解即可.
【详解】解:先按MODE,选择模式;再键tan,35,最后按=;可得到这个角的函数值.
故答案为:MODE,tan,35,=
【点睛】本题考查计算器—三角函数,要求同学们能熟练应用计算器,会用计算器进行计算.
15.或
【详解】解方程x2-4x+3=0得,x1=1,x2=3,
①当3是直角边时,∵△ABC最小的角为A,∴tanA=;
②当3是斜边时,根据勾股定理,∠A的邻边=,∴tanA=;
所以tanA的值为或.
16.3
【分析】根据, ,,解直角三角形即可得到答案.
【详解】解:如图:在中,,
,,
,
故答案为:3.
【点睛】本题主要考查了解直角三角形,解题的关键在于能够熟练掌握相关知识进行求解.
17.50
【分析】根据正切三角函数计算求值即可.
【详解】解:由题意作图如下,
Rt△ABC中,∠C=90°,BC=20m,tan∠A=,
∴AC=BC÷tan∠A=20×=50m,
故答案为:50.
【点睛】本题考查了正切三角函数,掌握正切的概念是解题关键.
18.图(1),,;图(2),,;图(3),,
【分析】根据勾股定理求得另外一边的长度,在利用三角函数的定义求解即可.
【详解】解:由图(1)得,,
由勾股定理得:
,,
由图(2)得:,
由勾股定理得:
,,
由图(3)得:,
由勾股定理得:
,,
【点睛】此题考查了三角函数的定义,涉及了勾股定理,解题的关键是熟练掌握三角函数的有关定义.
19.(1)雕像的高度是
(2)测量者离雕像底部的距离为
【分析】(1)过点C作于F,在中,求出的长,在中,求出的长即可;
(2)过A作于G,求出,在中求出的长.
【详解】(1)过点C作于F
在中,
∴
在中,
答:雕像的高度是.
(2)过A作于G,则四边形为矩形
在中,由于
∴
在中,
∴
∴
答:测量者离雕像底部的距离为.
【点睛】本题考查了解直角三角形的应用仰角俯角问题,将解直角三角形与实际问题结合,需要构造合适的直角三角形.
20.(1)4
(2)
【分析】(1)连接.设的半径为R.在中,根据,构建方程即可解决问题;
(2)连接,根据可得,再由垂径定理可得,根据扇形的面积公式求解即可.
【详解】(1)解:如图,连接.设的半径为R.
∵,
∴,
在中,
∵,
∴,
解得.
(2)解:如图,连接,
∵,
∴,
∵,
∴
∴,
∴扇形的面积.
【点睛】本题考查的是特殊角的三角函数、圆周角定理的推论和垂径定理的应用,掌握圆周角定理的推论、垂径定理和勾股定理是解题的关键,学会添加常用辅助线.
21..
【分析】首先根据锐角三角形函数值的知识求出∠B的度数,进而求出BC的长度,在直角三角形中,利用30°的角所对的直角边等于斜边的一半求出AB的长.
【详解】在直角三角形ABC中,∠C=90°,
∵cosA=,
∴∠A=30°,
∴∠B=60°,
∵BD是∠B的平分线,
∴∠DBC=30°,
在直角三角形DBC中
cos30°=,
∴BC=16×=8,
在直角三角形ACB中,
∵∠A=30°,
∴30°的角所对的直角边等于斜边的一半,
∴AB=16.
【点睛】本题主要考查了解直角三角形的知识,解答本题的关键是掌握锐角三角形函数的定义以及含30°角直角三角形的性质,此题难度不大.
22.(1)证明见解析
(2)
【分析】(1)根据矩形的性质可知沿折叠为,得出,再根据三角形的内角和为180°,可知 得出 即可证明.
(2)已知 设 得出 由(1)中可得 .
【详解】(1)证明:∵四边形ABCD是矩形,
∴
∵△BCE沿BE折叠为△BFE,
,
又∵
∴∠ABF=∠DFE,
∴△ABF∽△DFE.
(2)在中,
∴设
∵沿折叠为,
又
.
【点睛】本题考查了矩形的性质,折叠的性质,三角形相似的判定和性质,正弦函数,正切函数,熟练掌握事件相似的相似和判定,灵活运用三角函数是解题的关键.
23.至少有13个台阶
【分析】根据含30度的直角三角形三边的关系和等腰直角三角形的性质得到BD和CE的长,即可解决问题.
【详解】解:∵AB部分的坡角为45°,AD=1.5m,
∴BD=AD=1.5m,
∴AB= m,
∵AB=BC,
∴BC= m,
∵BC部分的坡角为30°,
∴EC=BC=m,
∴BD+CE=(m),
∵每个台阶的高不超过20cm,
∴至少有台阶的数量为()×100÷20≈13.
【点睛】本题考查了坡度的概念:斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值,即斜坡的坡度等于斜坡的坡角的正弦.也考查了含30度的直角三角形三边的关系和等腰直角三角形的性质.
24.(1);(2)
【分析】本题考查了三角函数的应用、勾股定理:
(1)过M作平行的直线,与分别相交于,根据的三角函数得出和的长度,从而求出的长度;
(2)根据,,得出与的关系,然后根据的勾股定理得出的长度.
【详解】解:(1)过M作平行的直线,与分别相交于,
在中,,
所以(单位),
(单位)
所以铁环钩离地面的高度为;
(2)因为,,
所以,
即得,
在中,(单位),
由勾股定理,
即,
解得(单位),
即,
所以铁环钩的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
