28.1锐角三角函数同步强化练习(含解析)
文档属性
| 名称 | 28.1锐角三角函数同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,则的长为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,则cosA=( )
A. B. C. D.
4.如图,在的正方形网格中,的顶点都在格点上,则的正弦值是( )
A. B. C. D.
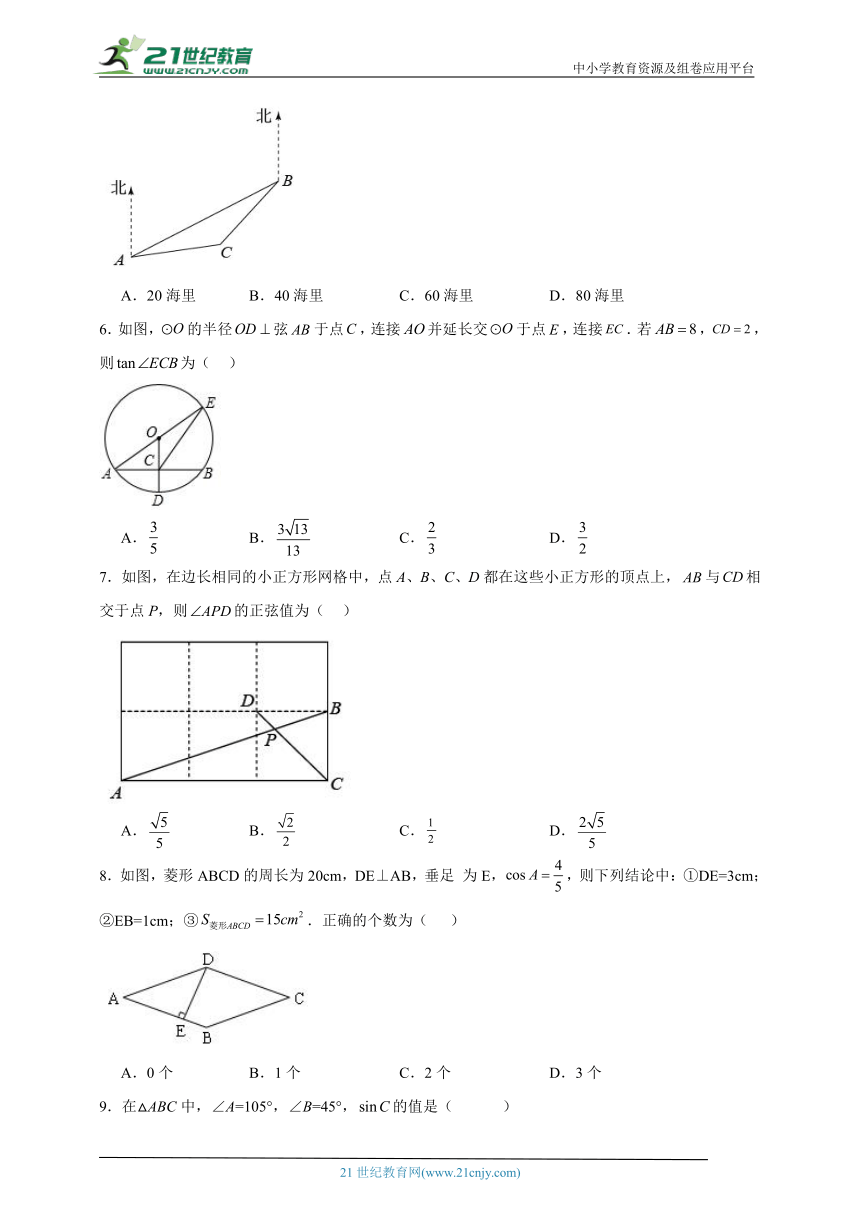
5.从观测点A测得海岛B在其北偏东60°方向上,测得海岛C在其北偏东80°方向上,若一艘小船从海岛B出发沿南偏西40°方向以每小时40海里的速度,行驶2小时到C海岛,则C海岛到观测点A的距离是( )
A.20海里 B.40海里 C.60海里 D.80海里
6.如图,的半径弦于点,连接并延长交于点,连接.若,,则为( )
A. B. C. D.
7.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,与相交于点P,则的正弦值为( )
A. B. C. D.
8.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足 为E,,则下列结论中:①DE=3cm;②EB=1cm;③.正确的个数为( )
A.0个 B.1个 C.2个 D.3个
9.在△ABC中,∠A=105°,∠B=45°,的值是( )
A. B. C.1 D.
10.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ= D.tanα=1
11.“新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A、B、C、D、E、F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)
A.200 B.250 C.300 D.540
12.数字,,π,,cos45°,中是无理数的个数有( )个.
A.1 B.2 C.3 D.4
二、填空题
13.计算= .
14.如图,在矩形ABCD中,对角线AC、BD相交于O,DE⊥AC于E,∠EDC:∠EDA=1:2,且AC=10,则DE的长度是
15.中,,,,则 .
16.等腰三角形的面积为24,底边长4,则底角的正切值为 .
17.求值: .
三、解答题
18.如图,在梯形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB、CD于点E、F,连接CE、AF.
(1)求证:四边形AECF是菱形;
(2)若EF=4,tan∠OAE=,求四边形AECF的面积.
19.如图,PB为的切线,B为切点,过B作OP的垂线BA,垂足为C,交于点A,连接PA,AO.并延长AO交于点E,与PB的延长线交于点D.
(1)求证:PA是的切线;
(2)若=,且OC=4,求PA的长和tan D的值.
20.阅读下列材料,并完成相应的任务.
初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系(如图):
.
一般地,当、为任意角时,与的值可以用下面的公式求得:
;
.
例如:.
根据上述材料内容,解决下列问题:
(1)计算:_______;
(2)在中,,请你求出和的长.
21.如图,在中,,为边上一点,以为圆心,长为半径的与边相切于点,交于点.
(1)求证:;
(2)连接,若,,求线段的长.
22.在Rt中,,,求的值.
23.求下列各式的值;
(1);
(2).
24.综合与实践
如下图,在边长为1的正方形网格中,连接格点、和、,和相交于点,求的值.
方法归纳:求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点,,可得,则,连接,那么就变换到中.
数学思考
(1)上图中______;
(2)如下图,,,,四点均在边长为1的正方形网格的格点上,与相交于点,求的值.
深入探究
(3)如下图,,,,,五点均在边长为1的正方形网格的格点上,交的延长线于点,求的值.
《28.1锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D D D D A C
题号 11 12
答案 B C
1.C
【分析】根据角的正弦值与三角形边的关系结合勾股定理即可求解.
【详解】∵在Rt△ABC中,∠C=90°,,,
∴,
设,则,
∵,即,
解得:,
∴,
故选:C.
【点睛】本题考查了锐角三角函数的定义以及勾股定理,熟记锐角三角函数的定义是解题的关键.
2.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【详解】解:∵∠C=90°,
∴=,
故选:A.
【点睛】此题主要考查了锐角三角函数的定义,关键是掌握余切定义.
3.B
【分析】过点D作DE⊥AB于E,设AB=AC=a,BC=b.根据等边对等角,三角形内角和定理求出∠ABC和∠C,根据角平分线的定义求出∠ABD和∠CBD,根据三角形外角的性质求出∠BDC,根据等角对等边确定AD=BD=BC,并用b表示出AD的长度,进而表示出DC的长度,根据该等腰三角形的性质用a来表示AE的长度,根据相似三角形的判定定理和性质列出比例式,并用a表示b,进而用a表示AD的长度,最后根据余弦的定义即可求解.
【详解】解:如下图所示,过点D作DE⊥AB于E,设AB=AC=a,BC=b.
∵AB=AC,∠A=36°,
∴.
∵BD平分∠ABC,
∴.
∴∠A=∠CBD=∠ABD,∠BDC=∠A+∠ABD=72°.
∴∠BDC=∠C,AD=BD.
∴AD=BD=BC=b.
∴.
∵DE⊥AB,
∴.
∵∠ACB=∠BCD,
∴.
∴.
∴.
∴用a表示b得,(舍).
∴.
∴.
∴.
故选:B.
【点睛】本题考查三角形内角和定理,角平分线的定义,等边对等角,等角对等边,三角形外角的性质,等腰三角形三线合一的性质,相似三角形的判定定理和性质,余弦的定义,综合应用这些知识点是解题关键.
4.B
【分析】先根据勾股定理的逆定理判断出的形状,再由锐角三角函数的定义即可得出结论.
【详解】解:,,,
,
为直角三角形,且,
则,
故选:B.
【点睛】本题考查的是勾股定理的逆定理以及锐角三角函数的定义,熟知在一个三角形中,如果两条边长的平方之和等于第三边长的平方,那么这个三角形是直角三角形是解答此题的关键.
5.D
【分析】利用平行线性质得出:∠ABD=∠EAB=60°,进而得出∠ABC=∠BAC=20°,得出BC=AC,进而得出答案.
【详解】解:由题意可得出:∠EAC=80°,∠EAB=60°,∠DBC=40°,BC=40×2=80(海里),
∴∠BAC=80°-60°=20°,∠BCA=60°,
∵AE∥BD,
∴∠ABD=∠EAB=60°,
∵∠DBC=40°,
∴∠ABC=60°-40°=20°,
∴∠ABC=∠BAC=20°,
∴BC=AC=80(海里).
∴C海岛到观测点A的距离是80海里.
故选D
.
【点睛】本题主要考查了解直角三角形的应用,利用方向角得出BC=AC是解题的关键.
6.D
【分析】根据垂径定理得到,设AO=x,则,在Rt△ACO中根据勾股定理得到,解得x=5,则OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中,由三角函数的定义求出即可.
【详解】连接,如图:
∵,∴,设,则,在中,∵,
∴,解得,
∴,∵是直径,∴,
∵是的中位线,∴,
∴.
故选:D.
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、三角函数;由勾股定理求出半径是解决问题的关键.
7.D
【分析】取格点,连接、,设网格中每个小正方形的边长为1,先证得,求得,再根据题意证得即可求解.
【详解】解:取格点,连接、,设网格中每个小正方形的边长为1,
则,,,
∵,,
∴,
∴,
在中,,
由题意知,,
∴,
∴,
∴,
故选:
【点睛】本题考查了网格问题中解直角三角形,构造直角三角形是解题的关键.
8.D
【详解】∵四边形ABCD是菱形,其周长=20cm,
∴AB=AD=5cm,
∵DE⊥AB于点E,
∴∠AED=90°,
∴cosA=,
∴AE=4cm,
∴BE=AB-AE=1cm,DE=cm,
∴S菱形ABCD=AB·DE=5×3=15cm2.
综上所述,题中所给三个结论都是正确的.
故选D.
9.A
【分析】先求出∠C=30°,再求出的值即可.
【详解】解:△ABC中,∵∠A=105°,∠B=45°,
∴∠C=180°-105°-45°=30°,
∴
故选:A
【点睛】本题主要考查三角形内角和公式,正弦定理,解决本题的关键是熟练掌握特殊角的三角函数值.
10.C
【详解】试题分析:由图可分别求得BD=AD=2,AB=2,CD=1,AC=,利用锐角三角函数定义在Rt△ABD和Rt△ACD中计算即可判断.
解:由图可得BD=AD=2,CD=1,
所以AB==2,AC==,
在Rt△ABD中,sinα==,cosα==,tanα==1,
在Rt△ACD中,sinβ==,cosβ==,tanC==2,
则sinα=cosα,故A正确;tanC=2,故B正确;sinβ≠cosβ,故C错误;tanα=1,故D正确.
故选C.
11.B
【分析】根据坡度的概念和俯角的概念解答即可.
【详解】解:由题意得,∠EAC=45°,EC=100米,
∴AC=EC=100米,
∵BE的坡度为1:3,
∴BC=3EC=300米,
∴AB=300+100=400米,
设DF=x米,
∵BE的坡度为1:3,
∴BD=3DF=3x米,
∵∠DAF=12°,tan12°≈0.2,
∴AD=5DF=5x米,
则8x=400,
解得x=50,
∴AD=250米.
故选B.
【点睛】本题考查的是解直角三角形、熟记锐角三角函数的定义、根据题意列出方程是解题的关键.
12.C
【详解】∵,cos45°=,
∴数字,,π,,cos45°,中属于无理数的有:,π,cos45°,共3个.
故选C.
13.3
【分析】根据特殊角的正切函数值、二次根式的乘法即可得.
【详解】,
故答案为:3.
【点睛】本题考查了特殊角的正切函数值、二次根式的乘法,熟记特殊角的正切值是解题关键.
14.
【分析】由题意得,,有,由,求出的值,由,求出的值即可.
【详解】解:∵四边形ABCD是矩形,
∴,
∵,
∴,
∴
∵
解得
∵
解得
故答案为:.
【点睛】本题考查了矩形的性质,特殊角的三角函数值.解题的关键在于根据特殊角的三角函数值求线段长.
15.6.5
【分析】直接利用锐角三角函数关系进而得出AB的值.
【详解】解:∵△ABC中,∠C=90°,BC=2.5,=,
∴,
∴AB=6.5.
故答案为6.5.
【点睛】锐角三角形正弦(sin)等于对边比斜边;=,正确掌握边角关系是解题关键.
16.6
【详解】试题分析:等腰三角形的面积为24,底边为4,设高为h,根据题意可得,h=12
所以,底角的正切值==6,故答案为6.
考点:1.等腰三角形的性质;2.锐角三角形函数
17.
【分析】根据特殊角的三角函数值直接得出答案即可.
【详解】tan60°的值为.
故答案为.
【点睛】本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.
18.(1)证明详见解析;(2)20.
【详解】试题分析:(1)运用“对角线互相垂直平分的四边形是菱形”判定,已知EF⊥AC,AO=OC,只需要证明OE=OF即可,用全等三角形得出;
(2)菱形的面积可以用对角线积的一半来表示,由已知条件,解直角三角形AOE可求AC、EF的长度.
试题解析:(1)证明:方法1:
∵AB∥DC,
∴∠1=∠2.
在△CFO和△AEO中,∠1=∠2,∠FOC=∠EOA,OC=OA,
∴△CFO≌△AEO,
∴OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
方法2:证△AEO≌△CFO同方法1,
∴CF=AE,
∵CF∥AE,
∴四边形AFCE是平行四边形.
∵OA=OC,EF⊥AC,
∴EF是AC的垂直平分线,
∴AF=CF,
∴四边形AECF是菱形.
(2)解:∵四边形AECF是菱形,EF=4,
∴OE=EF=×4=2.
在Rt△AEO中,
∵tan∠OAE=,
∴OA=5,
∴AC=2AO=2×5=10.
∴=EF AC=×4×10=20.
考点:菱形的判定;全等三角形的判定与性质;解直角三角形.
19.(1)证明见解析;(2)PA =3,tan D=.
【分析】(1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
【详解】解:(1)连接OB,则OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
∵,且OC=4,
∴AC=6,∴AB=12,
在Rt△ACO中,由勾股定理得:AO=,
∴AE=2OA=4,OB=OA=2,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OCPC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP==3.
易证,
所以,
解得,
则,
在中,.
考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.
20.(1);(2),
【分析】(1)根据题干中的公式可求.
(2)根据锐角的三角函数值,求AC和BC的值
【详解】解:
(2)中,∵,
∴.
∵,
∴.
【点睛】本题考查了同角三角函数关系,合理利用题干中告知的公式是本题的关键.
21.(1)见解析;(2)
【分析】(1)运用切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,题中已知,所以,切于点B,同时切于点,即可求证;
(2)连接,可得,由(1)得,根据各个角之间的关系可得,所以,依据正切定义可得,再根据三角形相似判别及性质,对应边成比例,即可得出答案.
【详解】(1)证明:
∵,
∴,
又∵经过半径的外端点,
∴切于点,
与边相切于点,
∴.
(2)解:连接,∵为的直径,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
即,
∵,
∴,,
又∵,,
∴,
∴,
设,则,
∴,
∴(舍去),.
即线段的长为.
【点睛】题目主要考查切线长定理、圆内三角形基本性质、三角函数、相似三角形的判别及性质等知识点,难点在于对定理得熟练掌握理解和对这些知识点的融会贯通.
22.
【分析】根据锐角三角函数值解答.
【详解】解:==.
【点睛】此题考查锐角三角函数值,熟记各角度的三角函数值是解题的关键.
23.(1);(2)
【分析】结合三角函数值计算即可.
【详解】解:(1)原式;
(2)原式.
【点睛】本题主要考查三角函数值的计算,属于基础的计算题型,难度不大.解题的关键是掌握特殊的三角函数值即可.
24.(1)(2)(3)
【分析】本题考查了平行线的性质,勾股定理及逆定理,平行四边形的判定,求一般角的三角函数值;
(1)可证,从而可得,可得,由勾股定理、的长,由即可求解;
(2)取格点,连接,,可证,从而可得,由勾股定理、的长,由即可求解;
(3)取格点,连接,,可证,从而可得,判定是直角三角形,由即可求解;
根据题意构建出适合的直角三角形是解题的关键.
【详解】解:(1)、是正方形小方格的对角线,
,
,
,
由图得:
,
,
,
,
;
故答案:;
(2)如图,取格点,连接,,
由图得:
,
,
,
,
,
;
(3)如图,取格点,连接,,
,,
四边形是平行四边形,
,
,
,
,
,
,
,
,
是直角三角形,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,则的长为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,则cosA=( )
A. B. C. D.
4.如图,在的正方形网格中,的顶点都在格点上,则的正弦值是( )
A. B. C. D.
5.从观测点A测得海岛B在其北偏东60°方向上,测得海岛C在其北偏东80°方向上,若一艘小船从海岛B出发沿南偏西40°方向以每小时40海里的速度,行驶2小时到C海岛,则C海岛到观测点A的距离是( )
A.20海里 B.40海里 C.60海里 D.80海里
6.如图,的半径弦于点,连接并延长交于点,连接.若,,则为( )
A. B. C. D.
7.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,与相交于点P,则的正弦值为( )
A. B. C. D.
8.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足 为E,,则下列结论中:①DE=3cm;②EB=1cm;③.正确的个数为( )
A.0个 B.1个 C.2个 D.3个
9.在△ABC中,∠A=105°,∠B=45°,的值是( )
A. B. C.1 D.
10.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ= D.tanα=1
11.“新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A、B、C、D、E、F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)
A.200 B.250 C.300 D.540
12.数字,,π,,cos45°,中是无理数的个数有( )个.
A.1 B.2 C.3 D.4
二、填空题
13.计算= .
14.如图,在矩形ABCD中,对角线AC、BD相交于O,DE⊥AC于E,∠EDC:∠EDA=1:2,且AC=10,则DE的长度是
15.中,,,,则 .
16.等腰三角形的面积为24,底边长4,则底角的正切值为 .
17.求值: .
三、解答题
18.如图,在梯形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB、CD于点E、F,连接CE、AF.
(1)求证:四边形AECF是菱形;
(2)若EF=4,tan∠OAE=,求四边形AECF的面积.
19.如图,PB为的切线,B为切点,过B作OP的垂线BA,垂足为C,交于点A,连接PA,AO.并延长AO交于点E,与PB的延长线交于点D.
(1)求证:PA是的切线;
(2)若=,且OC=4,求PA的长和tan D的值.
20.阅读下列材料,并完成相应的任务.
初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系(如图):
.
一般地,当、为任意角时,与的值可以用下面的公式求得:
;
.
例如:.
根据上述材料内容,解决下列问题:
(1)计算:_______;
(2)在中,,请你求出和的长.
21.如图,在中,,为边上一点,以为圆心,长为半径的与边相切于点,交于点.
(1)求证:;
(2)连接,若,,求线段的长.
22.在Rt中,,,求的值.
23.求下列各式的值;
(1);
(2).
24.综合与实践
如下图,在边长为1的正方形网格中,连接格点、和、,和相交于点,求的值.
方法归纳:求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点,,可得,则,连接,那么就变换到中.
数学思考
(1)上图中______;
(2)如下图,,,,四点均在边长为1的正方形网格的格点上,与相交于点,求的值.
深入探究
(3)如下图,,,,,五点均在边长为1的正方形网格的格点上,交的延长线于点,求的值.
《28.1锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D D D D A C
题号 11 12
答案 B C
1.C
【分析】根据角的正弦值与三角形边的关系结合勾股定理即可求解.
【详解】∵在Rt△ABC中,∠C=90°,,,
∴,
设,则,
∵,即,
解得:,
∴,
故选:C.
【点睛】本题考查了锐角三角函数的定义以及勾股定理,熟记锐角三角函数的定义是解题的关键.
2.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【详解】解:∵∠C=90°,
∴=,
故选:A.
【点睛】此题主要考查了锐角三角函数的定义,关键是掌握余切定义.
3.B
【分析】过点D作DE⊥AB于E,设AB=AC=a,BC=b.根据等边对等角,三角形内角和定理求出∠ABC和∠C,根据角平分线的定义求出∠ABD和∠CBD,根据三角形外角的性质求出∠BDC,根据等角对等边确定AD=BD=BC,并用b表示出AD的长度,进而表示出DC的长度,根据该等腰三角形的性质用a来表示AE的长度,根据相似三角形的判定定理和性质列出比例式,并用a表示b,进而用a表示AD的长度,最后根据余弦的定义即可求解.
【详解】解:如下图所示,过点D作DE⊥AB于E,设AB=AC=a,BC=b.
∵AB=AC,∠A=36°,
∴.
∵BD平分∠ABC,
∴.
∴∠A=∠CBD=∠ABD,∠BDC=∠A+∠ABD=72°.
∴∠BDC=∠C,AD=BD.
∴AD=BD=BC=b.
∴.
∵DE⊥AB,
∴.
∵∠ACB=∠BCD,
∴.
∴.
∴.
∴用a表示b得,(舍).
∴.
∴.
∴.
故选:B.
【点睛】本题考查三角形内角和定理,角平分线的定义,等边对等角,等角对等边,三角形外角的性质,等腰三角形三线合一的性质,相似三角形的判定定理和性质,余弦的定义,综合应用这些知识点是解题关键.
4.B
【分析】先根据勾股定理的逆定理判断出的形状,再由锐角三角函数的定义即可得出结论.
【详解】解:,,,
,
为直角三角形,且,
则,
故选:B.
【点睛】本题考查的是勾股定理的逆定理以及锐角三角函数的定义,熟知在一个三角形中,如果两条边长的平方之和等于第三边长的平方,那么这个三角形是直角三角形是解答此题的关键.
5.D
【分析】利用平行线性质得出:∠ABD=∠EAB=60°,进而得出∠ABC=∠BAC=20°,得出BC=AC,进而得出答案.
【详解】解:由题意可得出:∠EAC=80°,∠EAB=60°,∠DBC=40°,BC=40×2=80(海里),
∴∠BAC=80°-60°=20°,∠BCA=60°,
∵AE∥BD,
∴∠ABD=∠EAB=60°,
∵∠DBC=40°,
∴∠ABC=60°-40°=20°,
∴∠ABC=∠BAC=20°,
∴BC=AC=80(海里).
∴C海岛到观测点A的距离是80海里.
故选D
.
【点睛】本题主要考查了解直角三角形的应用,利用方向角得出BC=AC是解题的关键.
6.D
【分析】根据垂径定理得到,设AO=x,则,在Rt△ACO中根据勾股定理得到,解得x=5,则OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中,由三角函数的定义求出即可.
【详解】连接,如图:
∵,∴,设,则,在中,∵,
∴,解得,
∴,∵是直径,∴,
∵是的中位线,∴,
∴.
故选:D.
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、三角函数;由勾股定理求出半径是解决问题的关键.
7.D
【分析】取格点,连接、,设网格中每个小正方形的边长为1,先证得,求得,再根据题意证得即可求解.
【详解】解:取格点,连接、,设网格中每个小正方形的边长为1,
则,,,
∵,,
∴,
∴,
在中,,
由题意知,,
∴,
∴,
∴,
故选:
【点睛】本题考查了网格问题中解直角三角形,构造直角三角形是解题的关键.
8.D
【详解】∵四边形ABCD是菱形,其周长=20cm,
∴AB=AD=5cm,
∵DE⊥AB于点E,
∴∠AED=90°,
∴cosA=,
∴AE=4cm,
∴BE=AB-AE=1cm,DE=cm,
∴S菱形ABCD=AB·DE=5×3=15cm2.
综上所述,题中所给三个结论都是正确的.
故选D.
9.A
【分析】先求出∠C=30°,再求出的值即可.
【详解】解:△ABC中,∵∠A=105°,∠B=45°,
∴∠C=180°-105°-45°=30°,
∴
故选:A
【点睛】本题主要考查三角形内角和公式,正弦定理,解决本题的关键是熟练掌握特殊角的三角函数值.
10.C
【详解】试题分析:由图可分别求得BD=AD=2,AB=2,CD=1,AC=,利用锐角三角函数定义在Rt△ABD和Rt△ACD中计算即可判断.
解:由图可得BD=AD=2,CD=1,
所以AB==2,AC==,
在Rt△ABD中,sinα==,cosα==,tanα==1,
在Rt△ACD中,sinβ==,cosβ==,tanC==2,
则sinα=cosα,故A正确;tanC=2,故B正确;sinβ≠cosβ,故C错误;tanα=1,故D正确.
故选C.
11.B
【分析】根据坡度的概念和俯角的概念解答即可.
【详解】解:由题意得,∠EAC=45°,EC=100米,
∴AC=EC=100米,
∵BE的坡度为1:3,
∴BC=3EC=300米,
∴AB=300+100=400米,
设DF=x米,
∵BE的坡度为1:3,
∴BD=3DF=3x米,
∵∠DAF=12°,tan12°≈0.2,
∴AD=5DF=5x米,
则8x=400,
解得x=50,
∴AD=250米.
故选B.
【点睛】本题考查的是解直角三角形、熟记锐角三角函数的定义、根据题意列出方程是解题的关键.
12.C
【详解】∵,cos45°=,
∴数字,,π,,cos45°,中属于无理数的有:,π,cos45°,共3个.
故选C.
13.3
【分析】根据特殊角的正切函数值、二次根式的乘法即可得.
【详解】,
故答案为:3.
【点睛】本题考查了特殊角的正切函数值、二次根式的乘法,熟记特殊角的正切值是解题关键.
14.
【分析】由题意得,,有,由,求出的值,由,求出的值即可.
【详解】解:∵四边形ABCD是矩形,
∴,
∵,
∴,
∴
∵
解得
∵
解得
故答案为:.
【点睛】本题考查了矩形的性质,特殊角的三角函数值.解题的关键在于根据特殊角的三角函数值求线段长.
15.6.5
【分析】直接利用锐角三角函数关系进而得出AB的值.
【详解】解:∵△ABC中,∠C=90°,BC=2.5,=,
∴,
∴AB=6.5.
故答案为6.5.
【点睛】锐角三角形正弦(sin)等于对边比斜边;=,正确掌握边角关系是解题关键.
16.6
【详解】试题分析:等腰三角形的面积为24,底边为4,设高为h,根据题意可得,h=12
所以,底角的正切值==6,故答案为6.
考点:1.等腰三角形的性质;2.锐角三角形函数
17.
【分析】根据特殊角的三角函数值直接得出答案即可.
【详解】tan60°的值为.
故答案为.
【点睛】本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.
18.(1)证明详见解析;(2)20.
【详解】试题分析:(1)运用“对角线互相垂直平分的四边形是菱形”判定,已知EF⊥AC,AO=OC,只需要证明OE=OF即可,用全等三角形得出;
(2)菱形的面积可以用对角线积的一半来表示,由已知条件,解直角三角形AOE可求AC、EF的长度.
试题解析:(1)证明:方法1:
∵AB∥DC,
∴∠1=∠2.
在△CFO和△AEO中,∠1=∠2,∠FOC=∠EOA,OC=OA,
∴△CFO≌△AEO,
∴OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
方法2:证△AEO≌△CFO同方法1,
∴CF=AE,
∵CF∥AE,
∴四边形AFCE是平行四边形.
∵OA=OC,EF⊥AC,
∴EF是AC的垂直平分线,
∴AF=CF,
∴四边形AECF是菱形.
(2)解:∵四边形AECF是菱形,EF=4,
∴OE=EF=×4=2.
在Rt△AEO中,
∵tan∠OAE=,
∴OA=5,
∴AC=2AO=2×5=10.
∴=EF AC=×4×10=20.
考点:菱形的判定;全等三角形的判定与性质;解直角三角形.
19.(1)证明见解析;(2)PA =3,tan D=.
【分析】(1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
【详解】解:(1)连接OB,则OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
∵,且OC=4,
∴AC=6,∴AB=12,
在Rt△ACO中,由勾股定理得:AO=,
∴AE=2OA=4,OB=OA=2,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OCPC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP==3.
易证,
所以,
解得,
则,
在中,.
考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.
20.(1);(2),
【分析】(1)根据题干中的公式可求.
(2)根据锐角的三角函数值,求AC和BC的值
【详解】解:
(2)中,∵,
∴.
∵,
∴.
【点睛】本题考查了同角三角函数关系,合理利用题干中告知的公式是本题的关键.
21.(1)见解析;(2)
【分析】(1)运用切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,题中已知,所以,切于点B,同时切于点,即可求证;
(2)连接,可得,由(1)得,根据各个角之间的关系可得,所以,依据正切定义可得,再根据三角形相似判别及性质,对应边成比例,即可得出答案.
【详解】(1)证明:
∵,
∴,
又∵经过半径的外端点,
∴切于点,
与边相切于点,
∴.
(2)解:连接,∵为的直径,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
即,
∵,
∴,,
又∵,,
∴,
∴,
设,则,
∴,
∴(舍去),.
即线段的长为.
【点睛】题目主要考查切线长定理、圆内三角形基本性质、三角函数、相似三角形的判别及性质等知识点,难点在于对定理得熟练掌握理解和对这些知识点的融会贯通.
22.
【分析】根据锐角三角函数值解答.
【详解】解:==.
【点睛】此题考查锐角三角函数值,熟记各角度的三角函数值是解题的关键.
23.(1);(2)
【分析】结合三角函数值计算即可.
【详解】解:(1)原式;
(2)原式.
【点睛】本题主要考查三角函数值的计算,属于基础的计算题型,难度不大.解题的关键是掌握特殊的三角函数值即可.
24.(1)(2)(3)
【分析】本题考查了平行线的性质,勾股定理及逆定理,平行四边形的判定,求一般角的三角函数值;
(1)可证,从而可得,可得,由勾股定理、的长,由即可求解;
(2)取格点,连接,,可证,从而可得,由勾股定理、的长,由即可求解;
(3)取格点,连接,,可证,从而可得,判定是直角三角形,由即可求解;
根据题意构建出适合的直角三角形是解题的关键.
【详解】解:(1)、是正方形小方格的对角线,
,
,
,
由图得:
,
,
,
,
;
故答案:;
(2)如图,取格点,连接,,
由图得:
,
,
,
,
,
;
(3)如图,取格点,连接,,
,,
四边形是平行四边形,
,
,
,
,
,
,
,
,
是直角三角形,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
