28.2解直角三角形及其应用同步强化练习(含解析)
文档属性
| 名称 | 28.2解直角三角形及其应用同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
28.2解直角三角形及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A.
B.
C.
D.
2.某校积极开展综合实践活动,一次九年级数学小组发现校园里有一棵被强台风摧折的大树,其残留的树桩DC的影子的一端E刚好与倒地的树梢重合,于是他们马上利用其测量旁边钟楼AB的高度.如图是根据测量活动场景抽象出的平面图形.活动中测得的数据如下:
①大树被摧折倒下的部分DE=10m;
②tan∠CDE=;
③点E到钟楼底部的距离EB=7m;
④钟楼AB的影长BF=(20+8)m;
⑤从D点看钟楼顶端A点的仰角为60°.
(点C,E,B,F在一条直线上).
请你选择几个需要的数据,用你喜欢的方法求钟楼AB的高度,则AB=( )
A.15m B.(15+6)m C.(12+6)m D.15m
3.如图,四边形ABCD为菱形,O为对角线AC的中点,,,则菱形的周长为( )
A.8 B.4 C. D.
4.在△ABC中,∠C=90°,AC=1,BC=,则∠B的度数是( )
A.30° B.45° C.60° D.90°
5.如图,港口A在观测站O的正东方向,OA=4km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.4km B.2km C.2km D.(+1)km
6.在△ABC中,∠C=90°,tanA=,△ABC的周长为60,那么△ABC的面积为( )
A.60 B.30 C.240 D.120
7.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
A.南偏东,千米 B.北偏西,千米
C.南偏东,100千米 D.北偏西,100千米
8.如图,一架无人机航拍过程中在C处测得地面上A,B两个目标点的俯角分别为30°和60°.若A,B两个目标点之间的距离是120米,则此时无人机与目标点A之间的距离(即AC的长)为( )
A.120米 B.米
C.60米 D.米
9.在Rt△ABC中,∠C=90°,cosA=,则sinA的值是( )
A. B. C. D.
10.如图,用三角支架固定空调外机,已知,,米,则点O到墙面距离为( )
A.米 B.米 C.米 D.米
11.若把一个直角三角形的两条直角边都扩大倍,(是大于的自然数),则两个锐角的三角函数值( )
A.都变大为原来的倍 B.都缩小为原来的
C.不变化 D.各个函数值变化不一致
12.如图,菱形的一边在轴上,,,将菱形绕原点逆时针方向旋转75°,得到菱形,则顶点的对应点的坐标是( )
A. B. C. D.
二、填空题
13.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆的长 .
14.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .
15.如图,和分别是的直径和弦,且,交于点,若,则 .
16.如图,从地面上的点看一山坡上的电线杆,测得杆顶端点的仰角是,向前走到达点,测得杆顶端点和杆底端点的仰角分别是和.则该电线杆的高度是 (结果可保留根号).
17.如图,某商场自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,则该扶梯的坡度是 .
三、解答题
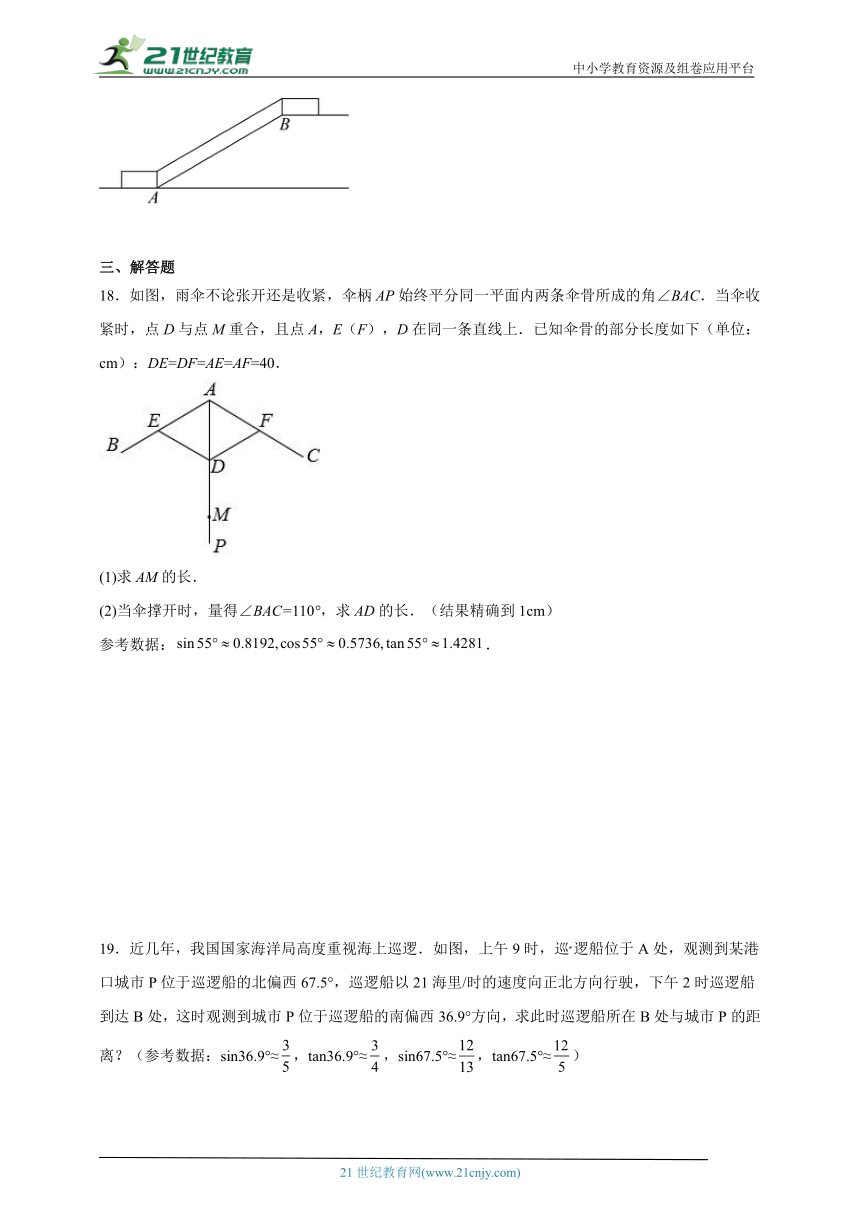
18.如图,雨伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时,点D与点M重合,且点A,E(F),D在同一条直线上.已知伞骨的部分长度如下(单位:cm):DE=DF=AE=AF=40.
(1)求AM的长.
(2)当伞撑开时,量得∠BAC=110°,求AD的长.(结果精确到1cm)
参考数据:.
19.近几年,我国国家海洋局高度重视海上巡逻.如图,上午9时,巡逻船位于A处,观测到某港口城市P位于巡逻船的北偏西67.5°,巡逻船以21海里/时的速度向正北方向行驶,下午2时巡逻船到达B处,这时观测到城市P位于巡逻船的南偏西36.9°方向,求此时巡逻船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
20.如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米米、坡角为的斜坡通道改造成坡角为的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长结果精确到米参考数据:.
21.如图,某货船以20海里/小时的速度将一批重要的物资由A处运往正西方向的B处,经16小时的航行到达,到达后便接到气象部门通知,一台风中心正由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.在B处的货船是否会受到台风的侵袭?说明理由.
22.某学校A位于工地O的正西方向,且,一辆货车从O处出发,以的速度沿北偏西方向行驶.已知货车的噪声污染半径为,那么学校是否在该货车噪声污染范围内?若在,则学校受该货车噪声污染的时间有几秒?(结果精确到)
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
24.如图,Rt△ABC中,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE.使,连接CE.则:
(1)求证:;
(2)若,求证:.
《28.2解直角三角形及其应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A C D B B A B
题号 11 12
答案 C D
1.D
【分析】连接OC、OA、BD,作OH⊥AC于H.首先求出AC的长,利用三角形的中位线定理即可解决问题.
【详解】解:连接OC、OA、BD,作OH⊥AC于H.
∵∠AOC=2∠ABC=120°,
∵OA=OC,OH⊥AC,
∴∠COH=∠AOH=60°,CH=AH,
∴CH=AH=OC sin60°=,
∴AC=,
∵CN=DN,DM=AM,
∴MN=,
∵CP=PB,AN=DN,
∴PN=,
当BD是直径时,PN的值最大,最大值为2,
∴PM+MN的最大值为.
故答案选:D.
【点睛】本题考查圆周角定理、三角形的中位线的定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
2.B
【分析】过D作DG⊥AB于G,则DG=BC,BG=CD,先求出CE=8(m),BG=CD=6(m),则DG=BC=CE+BE=15(m),再求出AG=DG=15,即可求解.
【详解】解:选择:①大树被摧折倒下的部分DE=10m;②tan∠CDE=;③点E到钟楼底部的距离EB=7m;⑤从D点看钟楼顶端A点的仰角为60°.理由如下:
过D作DG⊥AB于G,如图所示:
则DG=BC,BG=CD,
∵DE=10m,tan∠CDE==,
∴CE=8(m),BG=CD=6(m),
∴DG=BC=CE+BE=8+7=15(m),
在Rt△ADG中,∠ADG=60°,tan∠ADG==,
∴AG=DG=15,
∴AB=AG+BG=(15+6)m,
故选:B.
【点睛】本题考查解直角三角形的实际应用,熟练掌握三角函数的应用,利用特殊角,添加合适的辅助线构造直角三角形是本题的解题关键.
3.A
【分析】如图所示,连接BD,利用菱形的性质得到AC⊥BD,然后解直角△OAB求出AB的长即可得到答案.
【详解】解:如图所示,连接BD,
∵四边形ABCD是菱形,O是AC的中点,
∴AB=BC=CD=AD,O为BD中点,且AC⊥BD,
∵∠BAC=30°,
∴,
∴菱形的周长为AB+BC+CD+AD=8,
故选:A.
【点睛】本题主要考查了菱形的性质,解直角三角形,熟知菱形的性质是解题的关键.
4.A
【分析】根据题意可知在Rt△ABC中,∠C=90°,AC=1,BC=,从而算出tanB=;
接下来结合特殊角的三角函数值,求出∠B的度数,进而得到答案.
【详解】∵在Rt△ABC中,∠C=90°,AC=1,BC=,
∴tanB=,
∴∠B=30°.
故选A.
【点睛】本题是解直角三角形的问题,需要根据锐角三角函数的定义及特殊角的三角函数值进行解答.
5.C
【详解】试题分析:过点A作AD⊥OB,则AD=OA=2km,根据题意可得:△ABD为等腰直角三角形,则AB=2km.
考点:三角函数的应用
6.D
【分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.
【详解】如图所示,
由tanA=,
设BC=12x,AC=5x,根据勾股定理得:AB=13x,
由题意得:12x+5x+13x=60,
解得:x=2,
∴BC=24,AC=10,
则△ABC面积为120,
故选D.
【点睛】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.
7.B
【分析】根据题意得出AO=BO以及∠BOA=90°,进而得出第二艘快艇航行的方向和距离.
【详解】
解:∵第一艘快艇沿北偏西70°方向,第二艘快艇沿南偏西20°方向,
∴∠BOA=90°,
∵BO=AO=50km,
∴AB= km,∠B=∠OAB=45°,
∵第二艘快艇沿南偏西20°方向,
∴∠1=∠CAO=20°,
∴∠2=45° 20°=25°,
∴第二艘快艇航行的方向和距离分别是:北偏西25°,千米.
故答案选:B.
【点睛】本题主要考查了勾股定理以及方向角,正确把握方向角的定义是解题关键.
8.B
【分析】设CE=x米,根据正切的定义用x分别表示出AE、BE,根据题意列方程,解方程得到答案.
【详解】解:设CE=x米,
在Rt△ACE中,tan∠CAE=,
则AE=,
在Rt△BCE中,tan∠CBE=,
则BE=,
由题意得,,
解得,x=60,即CE=60,
则AC=2CE=120(米)
故选B.
【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
9.A
【分析】根据cosA=设AC=4x,则AB=5x,利用勾股定理求出BC的长,再根据公式求出sinA的值.
【详解】解:在Rt△ABC中,∠C=90°,cosA==,
设AC=4x,则AB=5x,
∴,
∴sinA=,
故选:A.
【点睛】此题考查解直角三角形,勾股定理,熟记各三角函数的计算公式是解题的关键.
10.B
【分析】利用,即可得出结果.
【详解】解:∵,,米,
∴,
∴米;
故选B.
【点睛】本题考查解直角三角形的应用.正确的识图,熟练掌握锐角三角函数的定义,是解题的关键.
11.C
【分析】若把一个直角三角形的两条直角边都扩大n倍,根据相似三角形的判定,可知这两个直角三角形相似,再由相似三角形的性质,得出对应角相等,根据锐角三角函数的定义,可知两个锐角的三角函数值不变.
【详解】解:若把一个直角三角形的两条直角边都扩大n倍,则这两个直角三角形相似,得到对应角相等,故两个锐角的三角函数值不变.
故选:C.
【点睛】本题主要考查了相似三角形的判定、性质以及锐角三角函数的定义.
12.D
【分析】如图所示,连接AC交OB于D,过点作⊥y轴于E,先解直角三角形求出,再由旋转的性质,,则,由此求解即可.
【详解】解:如图所示,连接AC交OB于D,过点作⊥y轴于E,
∵四边形OABC是菱形,∠OAB=120°,
∴∠AOC=60°,∠ODA=90°,OA=OC=2,CD=AD,OB=2OD,
∴,
∴,
由旋转的性质可知,,,
∴,
∴,,
∴点的坐标为,
故选D.
【点睛】本题主要考查了坐标与图形,旋转的性质,菱形的性质,解直角三角形,正确作出辅助线构造直角三角形是解题的关键.
13.
【分析】根据题意作出合适的辅助线,然后利用锐角三角函数即可表示出AB的长.
【详解】解:作AD⊥BC于点D,
则,
,
解得:米,
故答案为:.
【点睛】本题考查解直角三角形的应用、轴对称图形,解答本题的关键是明确题意,利用数形结合的思想解答.
14.
【分析】作BC⊥地面于点C,根据坡度的概念、勾股定理列式计算即可.
【详解】解:作BC⊥地面于点C,
设BC=x米,
∵传送带和地面所成斜坡AB的坡度为1:2,
∴AC=2x米,
由勾股定理得,AC2+BC2=AB2,即(2x)2+x2=52,
解得,x=(负值舍去),即BC=米,
故答案为:.
【点睛】本题考查的是解直角三角形的应用 坡度坡角问题,掌握坡度坡角的概念是解题的关键.
15.5
【分析】在中,已知了的长和的度数,求得的长,也就得到了直径的值,连接,同理可在中求出的长,由 即可得解.
【详解】解:连接
在中, ,
则,, ,
∵是的直径,
∴,
在中,,,
,
.
故答案为.
【点睛】此题主要考查了解直角三角形和圆周角定理的应用,熟练掌握以上知识点是解题的关键.
16.
【分析】延长交直线于点,设米,在和中,根据三角函数利用表示出和,根据即可列出方程求得的值,再在中,利用三角函数求得的长,则的长度即可求解.
【详解】延长交直线于点,设米,
在中,
∵,
∴米,
在中,
∵,米,
∴米.
∵米,
∴,
∴米,
∴米.
在中,
∵,,
∴米,
∴米.
【点睛】本题考查了仰角的定义,以及三角函数,正确求得的长度是解本题的关键.
17.
【分析】根据题意和勾股定理可以求得的长,从而可以解答本题.
【详解】如图所示,过点B作,
∵自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,
∴,
该扶梯的坡度是.
故答案为:.
【点睛】本题考查解直角三角形的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数和数形结合的思想解答.
18.(1)AM= 80cm
(2)AD≈46cm
【分析】(1)当伞收紧时,点D与点M重合,AM=AF+DF计算即可;
(2)过点E作EH⊥AD于点H,利用菱形对角线平分的性质,求得∠DAE,解直角三角形AEH即可解答;
【详解】(1)解:由题意得, AM=AE+DE=80cm
(2)解: 如图,过点E作EH⊥AD于点H,
由题意,在△AED中,EA=ED,则AD=2AH,
DE=DF=AE=AF=40cm,则AEDF是菱形,
∴=55°
在 Rt△AEH中,
∴AH=40 cos 55°,
AD=2AH ≈2×0.5736×40≈46cm
【点睛】本题考查了等腰三角形的性质,菱形的判定和性质,余弦三角函数;掌握用三角函数解直角三角形是解题关键.
19.100海里
【分析】过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.
【详解】解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,
∴AC=,
在Rt△PCB中,∵tan∠B=,
∴BC=,
∵AC+BC=AB=21×5,
∴,解得x=60,
∵,
∴(海里).
∴巡逻船所在B处与城市P的距离为100海里.
【点睛】本题考查了方向角问题,注意结合实际问题,利用解直角三角形的相关知识求解是解此题的关键,注意数形结合思想的应用.
20.31.8米
【详解】试题分析:先根据锐角三角函数的定义求出BC的长,在Rt△BDC中利用锐角三角函数的定义即可得出结论.
试题解析:∵BC⊥DC,∠BAC=20°30′,AB=20米,
∴sin∠BAC=,
∴BC=AB sin∠BAC=20×sin20°30′.
在Rt△BDC中,
∵∠BDC=12°30′,sin∠BDC=,即sin12°30′=,
∴BD=≈31.8(米).
答:改造后的斜坡通道BD的长约为31.8米.
21.B处的货船会受到影响.
【分析】本题实际上是求B到AC的距离,作BD⊥AC垂足为D.那么只要求出BD的长,就能判断出货船是否受影响,直角三角形ABD中,AB可以根据路程=速度×时间来求出.又已知了∠BAC的度数,因此BD就不难求出了.
【详解】
AB=16×20=320(海里),
作BD⊥AC垂足为D.
∵∠BAC=30°,∴sin30°=,BD=AB·sin30°=160.
∵160<200,∴B处的货船会受到影响.
【点睛】本题考查的是三角函数,熟练掌握特殊角度的三角函数值是解题的关键.
22.在噪声污染范围内,约.
【分析】问教室A是否在拖拉机的噪声污染范围内,其实就是问A到OM的距离是否大于污染半径130m,如果大于则不受影响,反正则受影响.如果过A作AB⊥OM于B,那么AB就是所求的线段.直角三角形AOB中,∠AOB的度数容易求得,又已知了OA的值,那么AB便可求出了.然后进行判断即可,算出学校从刚开始受到噪声污染到污染刚好消失这段时间内货车行驶的路程,再除以货车的速度就是学校受污染的时间.
【详解】解:如图,过点A作AB⊥OM于点B,
∵∠MON=53°,
∴∠AOM=90° 53°=37°.
在Rt△ABO中,
∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin37°≈120(m).
∵120m<130m.
∴教室A在拖拉机的噪声污染范围内.
设货车在C点时刚好对学校产生污染,在D点时污染刚好消失,如图所示,
如图,假设AD=AC=130m,
∵,
∴B为CD的中点,即BC=DB,
∴BC==50m,
∴BD=2BC=100m,
∴t===20s.
即:学校受噪声污染的时间为20秒.
【点睛】本题主要考查了解直角三角形的知识,解题的关键是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.
23.(1);(2)
【分析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=,然后根据BC=BD+DC即可求解.
(2)先由三角形的中线的定义求出CE的值,则DE=CE﹣CD,然后在Rt△ADE中根据正切函数的定义即可求解.
【详解】解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴.
∴.
∴.
(2)∵AE是BC边上的中线,∴CE=BC=.
∴DE=CE﹣CD=.
∴.
【点睛】本题考查了三角形的高、中线的定义,勾股定理,解直角三角形,难度中等,分别解Rt△ADC与Rt△ADB,得出DC=1,AB=3是解题的关键.
24.(1)见解析
(2)见解析
【分析】(1)由直角三角形斜边中线的性质可知,即得出,再结合题意,即得出,从而证明;
(2)过点E作于点H,由,即得出,,从而得出,得出.根据平行线的性质得出,从而得出.又易证,得出,即可证明.
【详解】(1)∵,点D是边BC的中点,
∴,
∴.
∵,
∴,
∴;
(2)如图,过点E作于点H,
∵,
∴,
∵,
∴,
∴.
∵,
∴,
∴.
又∵,DE=DE,
∴,
∴,
∴,即.
【点睛】本题考查直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定和性质,解直角三角形以及全等三角形的判定和性质.正确作出辅助线是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.2解直角三角形及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A.
B.
C.
D.
2.某校积极开展综合实践活动,一次九年级数学小组发现校园里有一棵被强台风摧折的大树,其残留的树桩DC的影子的一端E刚好与倒地的树梢重合,于是他们马上利用其测量旁边钟楼AB的高度.如图是根据测量活动场景抽象出的平面图形.活动中测得的数据如下:
①大树被摧折倒下的部分DE=10m;
②tan∠CDE=;
③点E到钟楼底部的距离EB=7m;
④钟楼AB的影长BF=(20+8)m;
⑤从D点看钟楼顶端A点的仰角为60°.
(点C,E,B,F在一条直线上).
请你选择几个需要的数据,用你喜欢的方法求钟楼AB的高度,则AB=( )
A.15m B.(15+6)m C.(12+6)m D.15m
3.如图,四边形ABCD为菱形,O为对角线AC的中点,,,则菱形的周长为( )
A.8 B.4 C. D.
4.在△ABC中,∠C=90°,AC=1,BC=,则∠B的度数是( )
A.30° B.45° C.60° D.90°
5.如图,港口A在观测站O的正东方向,OA=4km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.4km B.2km C.2km D.(+1)km
6.在△ABC中,∠C=90°,tanA=,△ABC的周长为60,那么△ABC的面积为( )
A.60 B.30 C.240 D.120
7.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
A.南偏东,千米 B.北偏西,千米
C.南偏东,100千米 D.北偏西,100千米
8.如图,一架无人机航拍过程中在C处测得地面上A,B两个目标点的俯角分别为30°和60°.若A,B两个目标点之间的距离是120米,则此时无人机与目标点A之间的距离(即AC的长)为( )
A.120米 B.米
C.60米 D.米
9.在Rt△ABC中,∠C=90°,cosA=,则sinA的值是( )
A. B. C. D.
10.如图,用三角支架固定空调外机,已知,,米,则点O到墙面距离为( )
A.米 B.米 C.米 D.米
11.若把一个直角三角形的两条直角边都扩大倍,(是大于的自然数),则两个锐角的三角函数值( )
A.都变大为原来的倍 B.都缩小为原来的
C.不变化 D.各个函数值变化不一致
12.如图,菱形的一边在轴上,,,将菱形绕原点逆时针方向旋转75°,得到菱形,则顶点的对应点的坐标是( )
A. B. C. D.
二、填空题
13.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆的长 .
14.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .
15.如图,和分别是的直径和弦,且,交于点,若,则 .
16.如图,从地面上的点看一山坡上的电线杆,测得杆顶端点的仰角是,向前走到达点,测得杆顶端点和杆底端点的仰角分别是和.则该电线杆的高度是 (结果可保留根号).
17.如图,某商场自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,则该扶梯的坡度是 .
三、解答题
18.如图,雨伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时,点D与点M重合,且点A,E(F),D在同一条直线上.已知伞骨的部分长度如下(单位:cm):DE=DF=AE=AF=40.
(1)求AM的长.
(2)当伞撑开时,量得∠BAC=110°,求AD的长.(结果精确到1cm)
参考数据:.
19.近几年,我国国家海洋局高度重视海上巡逻.如图,上午9时,巡逻船位于A处,观测到某港口城市P位于巡逻船的北偏西67.5°,巡逻船以21海里/时的速度向正北方向行驶,下午2时巡逻船到达B处,这时观测到城市P位于巡逻船的南偏西36.9°方向,求此时巡逻船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
20.如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米米、坡角为的斜坡通道改造成坡角为的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长结果精确到米参考数据:.
21.如图,某货船以20海里/小时的速度将一批重要的物资由A处运往正西方向的B处,经16小时的航行到达,到达后便接到气象部门通知,一台风中心正由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.在B处的货船是否会受到台风的侵袭?说明理由.
22.某学校A位于工地O的正西方向,且,一辆货车从O处出发,以的速度沿北偏西方向行驶.已知货车的噪声污染半径为,那么学校是否在该货车噪声污染范围内?若在,则学校受该货车噪声污染的时间有几秒?(结果精确到)
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
24.如图,Rt△ABC中,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE.使,连接CE.则:
(1)求证:;
(2)若,求证:.
《28.2解直角三角形及其应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A C D B B A B
题号 11 12
答案 C D
1.D
【分析】连接OC、OA、BD,作OH⊥AC于H.首先求出AC的长,利用三角形的中位线定理即可解决问题.
【详解】解:连接OC、OA、BD,作OH⊥AC于H.
∵∠AOC=2∠ABC=120°,
∵OA=OC,OH⊥AC,
∴∠COH=∠AOH=60°,CH=AH,
∴CH=AH=OC sin60°=,
∴AC=,
∵CN=DN,DM=AM,
∴MN=,
∵CP=PB,AN=DN,
∴PN=,
当BD是直径时,PN的值最大,最大值为2,
∴PM+MN的最大值为.
故答案选:D.
【点睛】本题考查圆周角定理、三角形的中位线的定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
2.B
【分析】过D作DG⊥AB于G,则DG=BC,BG=CD,先求出CE=8(m),BG=CD=6(m),则DG=BC=CE+BE=15(m),再求出AG=DG=15,即可求解.
【详解】解:选择:①大树被摧折倒下的部分DE=10m;②tan∠CDE=;③点E到钟楼底部的距离EB=7m;⑤从D点看钟楼顶端A点的仰角为60°.理由如下:
过D作DG⊥AB于G,如图所示:
则DG=BC,BG=CD,
∵DE=10m,tan∠CDE==,
∴CE=8(m),BG=CD=6(m),
∴DG=BC=CE+BE=8+7=15(m),
在Rt△ADG中,∠ADG=60°,tan∠ADG==,
∴AG=DG=15,
∴AB=AG+BG=(15+6)m,
故选:B.
【点睛】本题考查解直角三角形的实际应用,熟练掌握三角函数的应用,利用特殊角,添加合适的辅助线构造直角三角形是本题的解题关键.
3.A
【分析】如图所示,连接BD,利用菱形的性质得到AC⊥BD,然后解直角△OAB求出AB的长即可得到答案.
【详解】解:如图所示,连接BD,
∵四边形ABCD是菱形,O是AC的中点,
∴AB=BC=CD=AD,O为BD中点,且AC⊥BD,
∵∠BAC=30°,
∴,
∴菱形的周长为AB+BC+CD+AD=8,
故选:A.
【点睛】本题主要考查了菱形的性质,解直角三角形,熟知菱形的性质是解题的关键.
4.A
【分析】根据题意可知在Rt△ABC中,∠C=90°,AC=1,BC=,从而算出tanB=;
接下来结合特殊角的三角函数值,求出∠B的度数,进而得到答案.
【详解】∵在Rt△ABC中,∠C=90°,AC=1,BC=,
∴tanB=,
∴∠B=30°.
故选A.
【点睛】本题是解直角三角形的问题,需要根据锐角三角函数的定义及特殊角的三角函数值进行解答.
5.C
【详解】试题分析:过点A作AD⊥OB,则AD=OA=2km,根据题意可得:△ABD为等腰直角三角形,则AB=2km.
考点:三角函数的应用
6.D
【分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.
【详解】如图所示,
由tanA=,
设BC=12x,AC=5x,根据勾股定理得:AB=13x,
由题意得:12x+5x+13x=60,
解得:x=2,
∴BC=24,AC=10,
则△ABC面积为120,
故选D.
【点睛】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.
7.B
【分析】根据题意得出AO=BO以及∠BOA=90°,进而得出第二艘快艇航行的方向和距离.
【详解】
解:∵第一艘快艇沿北偏西70°方向,第二艘快艇沿南偏西20°方向,
∴∠BOA=90°,
∵BO=AO=50km,
∴AB= km,∠B=∠OAB=45°,
∵第二艘快艇沿南偏西20°方向,
∴∠1=∠CAO=20°,
∴∠2=45° 20°=25°,
∴第二艘快艇航行的方向和距离分别是:北偏西25°,千米.
故答案选:B.
【点睛】本题主要考查了勾股定理以及方向角,正确把握方向角的定义是解题关键.
8.B
【分析】设CE=x米,根据正切的定义用x分别表示出AE、BE,根据题意列方程,解方程得到答案.
【详解】解:设CE=x米,
在Rt△ACE中,tan∠CAE=,
则AE=,
在Rt△BCE中,tan∠CBE=,
则BE=,
由题意得,,
解得,x=60,即CE=60,
则AC=2CE=120(米)
故选B.
【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
9.A
【分析】根据cosA=设AC=4x,则AB=5x,利用勾股定理求出BC的长,再根据公式求出sinA的值.
【详解】解:在Rt△ABC中,∠C=90°,cosA==,
设AC=4x,则AB=5x,
∴,
∴sinA=,
故选:A.
【点睛】此题考查解直角三角形,勾股定理,熟记各三角函数的计算公式是解题的关键.
10.B
【分析】利用,即可得出结果.
【详解】解:∵,,米,
∴,
∴米;
故选B.
【点睛】本题考查解直角三角形的应用.正确的识图,熟练掌握锐角三角函数的定义,是解题的关键.
11.C
【分析】若把一个直角三角形的两条直角边都扩大n倍,根据相似三角形的判定,可知这两个直角三角形相似,再由相似三角形的性质,得出对应角相等,根据锐角三角函数的定义,可知两个锐角的三角函数值不变.
【详解】解:若把一个直角三角形的两条直角边都扩大n倍,则这两个直角三角形相似,得到对应角相等,故两个锐角的三角函数值不变.
故选:C.
【点睛】本题主要考查了相似三角形的判定、性质以及锐角三角函数的定义.
12.D
【分析】如图所示,连接AC交OB于D,过点作⊥y轴于E,先解直角三角形求出,再由旋转的性质,,则,由此求解即可.
【详解】解:如图所示,连接AC交OB于D,过点作⊥y轴于E,
∵四边形OABC是菱形,∠OAB=120°,
∴∠AOC=60°,∠ODA=90°,OA=OC=2,CD=AD,OB=2OD,
∴,
∴,
由旋转的性质可知,,,
∴,
∴,,
∴点的坐标为,
故选D.
【点睛】本题主要考查了坐标与图形,旋转的性质,菱形的性质,解直角三角形,正确作出辅助线构造直角三角形是解题的关键.
13.
【分析】根据题意作出合适的辅助线,然后利用锐角三角函数即可表示出AB的长.
【详解】解:作AD⊥BC于点D,
则,
,
解得:米,
故答案为:.
【点睛】本题考查解直角三角形的应用、轴对称图形,解答本题的关键是明确题意,利用数形结合的思想解答.
14.
【分析】作BC⊥地面于点C,根据坡度的概念、勾股定理列式计算即可.
【详解】解:作BC⊥地面于点C,
设BC=x米,
∵传送带和地面所成斜坡AB的坡度为1:2,
∴AC=2x米,
由勾股定理得,AC2+BC2=AB2,即(2x)2+x2=52,
解得,x=(负值舍去),即BC=米,
故答案为:.
【点睛】本题考查的是解直角三角形的应用 坡度坡角问题,掌握坡度坡角的概念是解题的关键.
15.5
【分析】在中,已知了的长和的度数,求得的长,也就得到了直径的值,连接,同理可在中求出的长,由 即可得解.
【详解】解:连接
在中, ,
则,, ,
∵是的直径,
∴,
在中,,,
,
.
故答案为.
【点睛】此题主要考查了解直角三角形和圆周角定理的应用,熟练掌握以上知识点是解题的关键.
16.
【分析】延长交直线于点,设米,在和中,根据三角函数利用表示出和,根据即可列出方程求得的值,再在中,利用三角函数求得的长,则的长度即可求解.
【详解】延长交直线于点,设米,
在中,
∵,
∴米,
在中,
∵,米,
∴米.
∵米,
∴,
∴米,
∴米.
在中,
∵,,
∴米,
∴米.
【点睛】本题考查了仰角的定义,以及三角函数,正确求得的长度是解本题的关键.
17.
【分析】根据题意和勾股定理可以求得的长,从而可以解答本题.
【详解】如图所示,过点B作,
∵自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,
∴,
该扶梯的坡度是.
故答案为:.
【点睛】本题考查解直角三角形的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数和数形结合的思想解答.
18.(1)AM= 80cm
(2)AD≈46cm
【分析】(1)当伞收紧时,点D与点M重合,AM=AF+DF计算即可;
(2)过点E作EH⊥AD于点H,利用菱形对角线平分的性质,求得∠DAE,解直角三角形AEH即可解答;
【详解】(1)解:由题意得, AM=AE+DE=80cm
(2)解: 如图,过点E作EH⊥AD于点H,
由题意,在△AED中,EA=ED,则AD=2AH,
DE=DF=AE=AF=40cm,则AEDF是菱形,
∴=55°
在 Rt△AEH中,
∴AH=40 cos 55°,
AD=2AH ≈2×0.5736×40≈46cm
【点睛】本题考查了等腰三角形的性质,菱形的判定和性质,余弦三角函数;掌握用三角函数解直角三角形是解题关键.
19.100海里
【分析】过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.
【详解】解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,
∴AC=,
在Rt△PCB中,∵tan∠B=,
∴BC=,
∵AC+BC=AB=21×5,
∴,解得x=60,
∵,
∴(海里).
∴巡逻船所在B处与城市P的距离为100海里.
【点睛】本题考查了方向角问题,注意结合实际问题,利用解直角三角形的相关知识求解是解此题的关键,注意数形结合思想的应用.
20.31.8米
【详解】试题分析:先根据锐角三角函数的定义求出BC的长,在Rt△BDC中利用锐角三角函数的定义即可得出结论.
试题解析:∵BC⊥DC,∠BAC=20°30′,AB=20米,
∴sin∠BAC=,
∴BC=AB sin∠BAC=20×sin20°30′.
在Rt△BDC中,
∵∠BDC=12°30′,sin∠BDC=,即sin12°30′=,
∴BD=≈31.8(米).
答:改造后的斜坡通道BD的长约为31.8米.
21.B处的货船会受到影响.
【分析】本题实际上是求B到AC的距离,作BD⊥AC垂足为D.那么只要求出BD的长,就能判断出货船是否受影响,直角三角形ABD中,AB可以根据路程=速度×时间来求出.又已知了∠BAC的度数,因此BD就不难求出了.
【详解】
AB=16×20=320(海里),
作BD⊥AC垂足为D.
∵∠BAC=30°,∴sin30°=,BD=AB·sin30°=160.
∵160<200,∴B处的货船会受到影响.
【点睛】本题考查的是三角函数,熟练掌握特殊角度的三角函数值是解题的关键.
22.在噪声污染范围内,约.
【分析】问教室A是否在拖拉机的噪声污染范围内,其实就是问A到OM的距离是否大于污染半径130m,如果大于则不受影响,反正则受影响.如果过A作AB⊥OM于B,那么AB就是所求的线段.直角三角形AOB中,∠AOB的度数容易求得,又已知了OA的值,那么AB便可求出了.然后进行判断即可,算出学校从刚开始受到噪声污染到污染刚好消失这段时间内货车行驶的路程,再除以货车的速度就是学校受污染的时间.
【详解】解:如图,过点A作AB⊥OM于点B,
∵∠MON=53°,
∴∠AOM=90° 53°=37°.
在Rt△ABO中,
∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin37°≈120(m).
∵120m<130m.
∴教室A在拖拉机的噪声污染范围内.
设货车在C点时刚好对学校产生污染,在D点时污染刚好消失,如图所示,
如图,假设AD=AC=130m,
∵,
∴B为CD的中点,即BC=DB,
∴BC==50m,
∴BD=2BC=100m,
∴t===20s.
即:学校受噪声污染的时间为20秒.
【点睛】本题主要考查了解直角三角形的知识,解题的关键是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.
23.(1);(2)
【分析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=,然后根据BC=BD+DC即可求解.
(2)先由三角形的中线的定义求出CE的值,则DE=CE﹣CD,然后在Rt△ADE中根据正切函数的定义即可求解.
【详解】解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴.
∴.
∴.
(2)∵AE是BC边上的中线,∴CE=BC=.
∴DE=CE﹣CD=.
∴.
【点睛】本题考查了三角形的高、中线的定义,勾股定理,解直角三角形,难度中等,分别解Rt△ADC与Rt△ADB,得出DC=1,AB=3是解题的关键.
24.(1)见解析
(2)见解析
【分析】(1)由直角三角形斜边中线的性质可知,即得出,再结合题意,即得出,从而证明;
(2)过点E作于点H,由,即得出,,从而得出,得出.根据平行线的性质得出,从而得出.又易证,得出,即可证明.
【详解】(1)∵,点D是边BC的中点,
∴,
∴.
∵,
∴,
∴;
(2)如图,过点E作于点H,
∵,
∴,
∵,
∴,
∴.
∵,
∴,
∴.
又∵,DE=DE,
∴,
∴,
∴,即.
【点睛】本题考查直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定和性质,解直角三角形以及全等三角形的判定和性质.正确作出辅助线是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
