29.2三视图同步强化练习(含解析)
文档属性
| 名称 | 29.2三视图同步强化练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 957.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:40:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
29.2三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列几何体中,主视图与俯视图不相同的是( )
A. B. C. D.
2.一个几何体的三视图如图所示,这个几何体是( )
A. B.
C. D.
3.由4个相同的小正方体搭建了一个积木,从正面、左面看搭建的积木的形状图如图所示,则这个积木不可能是下面四个立体图形中的( )
A. B. C. D.
4.如图是一根钢管的直观图,则它的三视图是( )
A.A B.B C.C D.D
5.如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图( )
A. B. C. D.
6.某几何体的三视图如图所示,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
7.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
8.如图是由5个大小相同的正方体摆成的立方体图形,它的俯视图是( )
A. B. C. D.
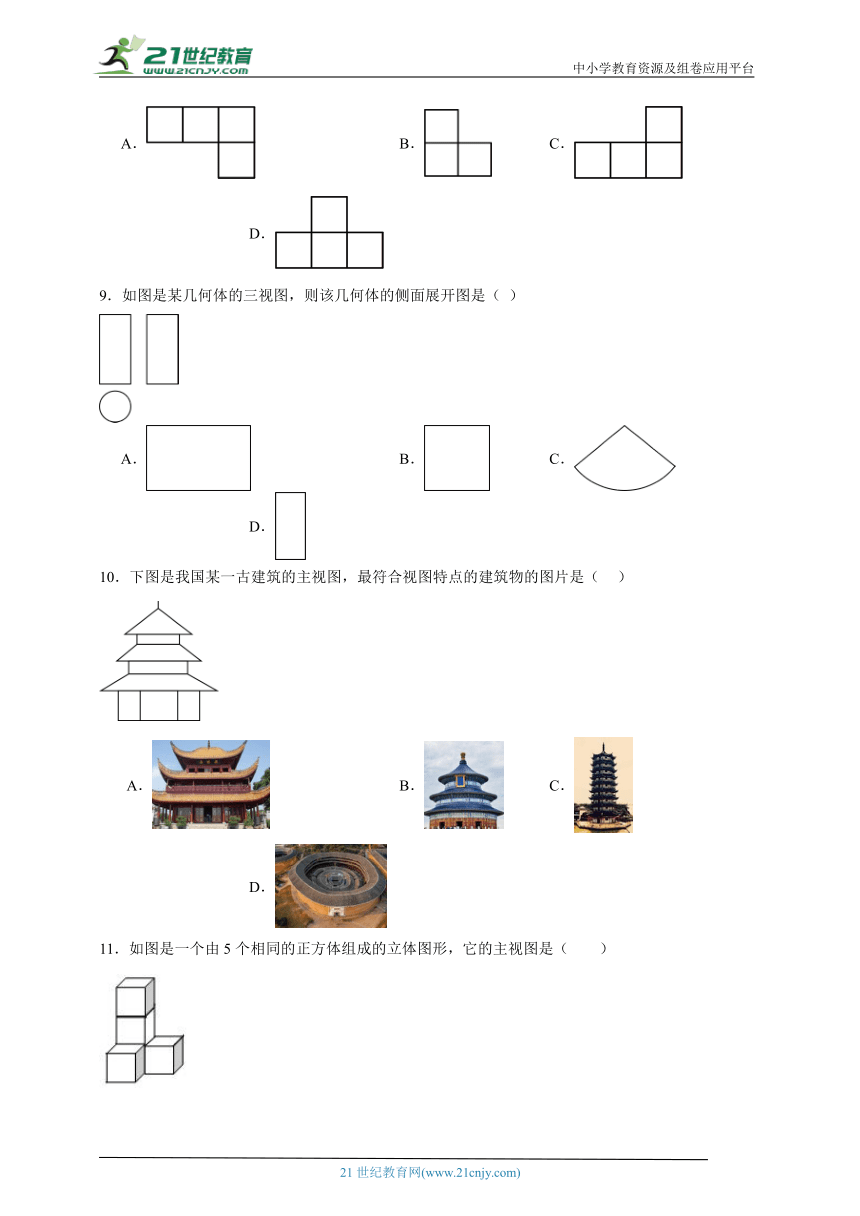
9.如图是某几何体的三视图,则该几何体的侧面展开图是( )
A. B. C. D.
10.下图是我国某一古建筑的主视图,最符合视图特点的建筑物的图片是( )
A. B. C. D.
11.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
12.为迎接端午节,超市用一些装有同种饮料的正方体纸箱做造型,其俯视图如图所示,其中正方形中的数字表示该位置上的正方体纸箱的个数,那么该造型的左视图是( )
A. B. C. D.
二、填空题
13.如图为由一些边长为1 cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是 cm2.
14.如图所示,桌面上放着一个圆柱和一个正方体.请你说出下面的三幅图的三视图.
, , .
15.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的主视图、左视图和俯视图中,随机抽取一个视图,则抽取的视图是轴对称图形的概率为
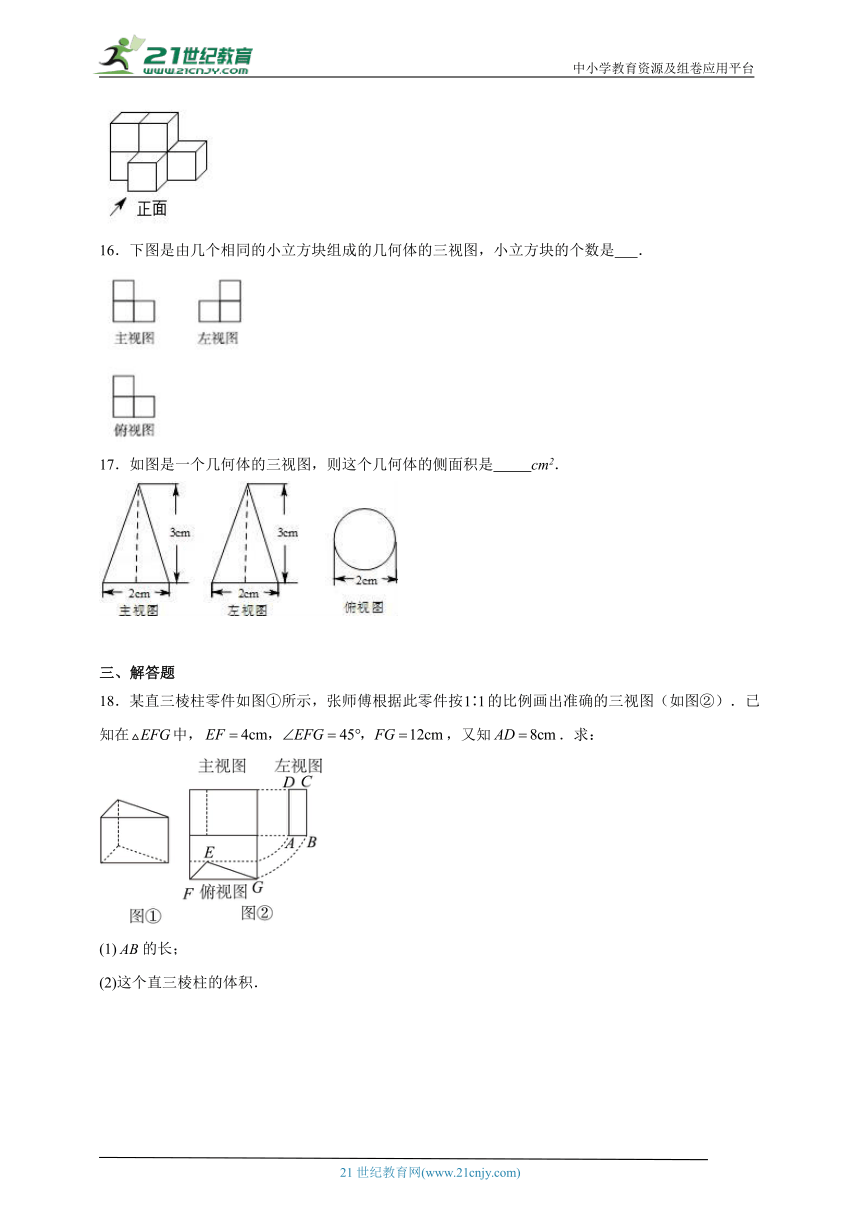
16.下图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是 .
17.如图是一个几何体的三视图,则这个几何体的侧面积是 cm2.
三、解答题
18.某直三棱柱零件如图①所示,张师傅根据此零件按的比例画出准确的三视图(如图②).已知在中,,又知.求:
(1)的长;
(2)这个直三棱柱的体积.
19.如图是由一些棱长均为1个单位长度的小正方体组合成的简单几何体.
(1)画该几何体的主视图、左视图:
(2)若给该几何体露在外面的面(不含底图)都喷上红漆,则需要喷漆的面积是 ;
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,则最多可以再添加 块小正方体.
20.某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:)
21.如果一个几何体从正面看、左面看、上面看看到的平面图形都是正方形,那么这个几何体可能是什么形状?
22.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将从正面、左面和上面看到的形状图画了出来(如图所示),则这堆正方体货箱共有多少箱?
23.如图是空心圆柱的两种视图,哪个有错误?为什么?
24.根据要求画出下列立体图形的视图.
《29.2三视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D A D A A A B
题号 11 12
答案 B B
1.B
【详解】分析:根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形进行分析.
详解:四棱锥的主视图与俯视图不同.
故选B.
点睛:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表示在三视图中.
2.A
【分析】本题考查了几何体的三视图,熟练掌握该知识点是解题的关键.根据三视图进行判断即可.
【详解】解:由三视图(主视图、左视图、俯视图)可知这个几何体的形状如下:
故选:A.
3.D
【分析】根据主视图即可判断出D为错误选项.
【详解】由D选项的主视图与图形的主视图不符
即可判断D为错误选项;
故选D.
【点睛】本题考查由三视图判断几何体,熟练掌握几何体的三视图的相关知识是解题关键.
4.D
【详解】根据左视图,正视图,俯视图的画法分别画出图形,钢管的左视图和正视图都是一个矩形,并且中间一个小矩形,小矩形的边是虚线,它的俯视图是两个圆,都是实线.
点睛:本题考查简单组合体的三视图的画法,主要培养学生的空间想象能力和动手操作能力.
5.A
【分析】根据三视图的特点,左视图从图形的左边向右看,看到一个正方形的面,在面上有一条实线,得到结果.
【详解】左视图从图形的左边向右看,看到一个正方形的面,在面上有一条实线,故选A.
【点睛】本题考查了三视图的定义,熟练掌握该定义可求解.
6.D
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形和圆心可判断出这个几何体应该是圆锥,
故选:D.
【点睛】本题考查由三视图判断几何体.
7.A
【详解】分析】直接利用左视图以及俯视图进而分析得出答案.
详解:由左视图可得,第2层上至少一个小立方体,
第1层一共有5个小立方体,故小正方体的个数最少为:6个,故小正方体的个数不可能是5个.
故选A.
点睛:此题主要考查了由三视图判断几何体,正确想象出最少时几何体的形状是解题关键.
8.A
【分析】找到从上面看所得到的图形即可.
【详解】解:从物体上面看,它的俯视图是
故选:A.
【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.
9.A
【详解】试题分析:根据几何体的三视图可以得到该几何体是圆柱,圆柱的侧面展开图是矩形,且高度=主视图的高,宽度=俯视图的周长.
故选A.
考点:1、由三视图判断几何体;2、几何体的展开图
10.B
【分析】依次观察各建筑物的图片即可作出判断,注意所有的看到的棱都应表现在主视图中.
【详解】解:最符合视图特点的建筑物的图片是选项B所示图片.
故选:B.
【点睛】本题考查三视图的知识,主视图是从物体的正面看得到的视图.
11.B
【分析】根据简单几何体的三视图即可判断.
【详解】由图形可知,主视图为
故选B.
【点睛】此题主要考查三视图的判断,解题的关键是熟知三视图的判断方法.
12.B
【分析】本题考查几何体的三视图画法.由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,1;据此可画出图形.
【详解】解:如图所示:
故选:B.
13.18 cm2
【分析】该几何体露在外面的部分是两个正视图,两个侧视图,一个俯视图面积的和,进而求得答案.
【详解】该几何体露在外面的部分是两个正视图,两个侧视图,一个俯视图面积和,
即.
【点睛】本题考查了几何体三视图和空间想象能力,熟练掌握三视图定义和充分发挥空间想象力是解题关键.
14. 俯视图 主视图 左视图
【详解】第一幅图是从上面看到的图形,是俯视图;第二幅图是从正面看到的图形,是主视图;第三幅图是从左面看到的图形,是左视图.
15.
【分析】分别画出这个几何体的三视图,然后根据轴对称图形的定义结合概率计算公式求解即可.
【详解】解:如图所示,该几何体的三视图为:
由三视图可知只有从上面看和从左面看的图形是轴对称图形,
∴抽取的视图是轴对称图形的概率为,
故答案为:.
【点睛】本题主要考查了简单几何组合体的三视图,轴对称图形的定义,简单的概率计算,正确画出三视图是解题的关键.
16.4个.
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从左视图可看出每一行小正方体的层数和个数,从而算出总的个数.
【详解】解:从俯视图上看,此几何体的下面有3个小正方体,
从左视图和主视图上看,最.上面有1个小正方体,
故组成这个几何体的小立方块的个数是:3+1=4.
故答案为: 4.
【点睛】此题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
17.
【详解】试题分析:由几何体的主视图和左视图都是等腰三角形,俯视图是圆,可以判断这个工件的几何体是圆锥.由等腰三角形的高为3,底面半径为1,可计算弧长,再根据圆锥侧面面积S=πrl计算.
试题解析:如图:
∵AO=3,CO=1,
∴AC=.
⊙O周长为2π.
∴此工件侧面积为.
考点:1.圆锥的计算;2.由三视图判断几何体.
18.(1)厘米
(2)立方厘米
【分析】本题考查了等腰直角三角形的判定与性质、勾股定理、三棱柱的三视图及三棱柱的体积计算:
(1)过点E作于点H,则根据题意可得出,然后由勾股定理计算即可得出答案;
(2)根据三棱柱的体积等于底面积乘以棱柱的高进行计算即可.
【详解】(1)解:过点E作于点H,如图.
在中,,
∴.
∴.
∴由勾股定理,得,
∴.
由图形可知.
(2)解:直三棱柱的体积.
19.(1)见详解;
(2)27;
(3)3.
【分析】(1)根据三视图的概念求解可得;
(2)将主视图、左视图分别乘2的面积,加上俯视图的面积即可得解;
(3)若使该几何体主视图和左视图不变,只可在底层添加方块,可以添加3块小正方体.
【详解】(1)如图所示:
(2)解:(7×2+4×2)×(1×1)+5×(1×1)
=14+8+5
=27
故答案为:27.
(3)若使该几何体主视图和左视图不变,可在最底层从右数第一至三列的第一行各添加一个,添加3块小正方体.
故答案为:3.
【点睛】本题主要考查了画三视图,解题的关键是掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都化成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方体的数目及位置.
20.每顶帐篷的表面积为96000πcm2.
【分析】根据三视图得到每顶帐篷由圆锥的侧面和圆柱的侧面组成,且圆锥的母线长为240cm,底面圆的半径为150cm,圆锥的高为200cm,由于圆锥的侧面展开图为一扇形,圆柱的侧面展开图为矩形,则根据扇形的面积公式和矩形的面积公式分别进行计算,然后求它们的和积.
【详解】解:根据三视图得圆锥的母线长为240cm,底面圆的半径为150cm,圆锥的高为200cm.
所以圆锥的侧面积= 2π 150 240=36000π,
圆柱的侧面积=2π 150 200=60000π,
所以每顶帐篷的表面积=36000π+60000π=96000π(cm2).
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.
21.正方体或正方体内部挖去一部分
【分析】由题意可知这个几何体不透明时,可能表面是正方体,而中间缺一部分.
【详解】由三视图是三个正方形可知,原立体图形应是四棱柱或挖去一部分的四棱柱.
因为正方形四边相等,四个角均为直角,可确定这个几何体是正方体.
【点睛】本题考查了正方体的三视图,从视图反过来考虑几何体,要注意考虑多种可能性,结合实物,亲自变换角度去观察,才能提高空间想象能力.
22.9箱
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】由题意可知,一共有三层正方体,
由俯视图可确定第一层有7个正方体
由主视图可知,第二层有1个正方体,第三层有1个正方体
即7+1+1=9(个)
故共有9箱正方体货箱.
【点睛】本题考查由三视图判断几何体,熟练掌握几何体的三视图的相关知识是解题关键.
23.(1)(2)是错误的,(3)是正确的,理由见解析.
【分析】分别找到从正面,从上面看所得到的图形即可,注意所有的棱都应表现在主视图和俯视图中.
【详解】如图所示,空心圆柱体的主视图是圆环;
俯视图是矩形,且有两条竖着的虚线.
∴(1)(2)是错误的,(3)是正确的
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
24.答案见解析.
【分析】根据主视图是从正面看到的图形,左视图是从左面看到的图形,俯视图是从上面看到的图形,即可得到结果.
【详解】解:如图所示:
【点睛】本题考查几何体的三视图,作图能力是学生必须具备的基本能力,因为此类问题在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
29.2三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列几何体中,主视图与俯视图不相同的是( )
A. B. C. D.
2.一个几何体的三视图如图所示,这个几何体是( )
A. B.
C. D.
3.由4个相同的小正方体搭建了一个积木,从正面、左面看搭建的积木的形状图如图所示,则这个积木不可能是下面四个立体图形中的( )
A. B. C. D.
4.如图是一根钢管的直观图,则它的三视图是( )
A.A B.B C.C D.D
5.如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图( )
A. B. C. D.
6.某几何体的三视图如图所示,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
7.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
8.如图是由5个大小相同的正方体摆成的立方体图形,它的俯视图是( )
A. B. C. D.
9.如图是某几何体的三视图,则该几何体的侧面展开图是( )
A. B. C. D.
10.下图是我国某一古建筑的主视图,最符合视图特点的建筑物的图片是( )
A. B. C. D.
11.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
12.为迎接端午节,超市用一些装有同种饮料的正方体纸箱做造型,其俯视图如图所示,其中正方形中的数字表示该位置上的正方体纸箱的个数,那么该造型的左视图是( )
A. B. C. D.
二、填空题
13.如图为由一些边长为1 cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是 cm2.
14.如图所示,桌面上放着一个圆柱和一个正方体.请你说出下面的三幅图的三视图.
, , .
15.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的主视图、左视图和俯视图中,随机抽取一个视图,则抽取的视图是轴对称图形的概率为
16.下图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是 .
17.如图是一个几何体的三视图,则这个几何体的侧面积是 cm2.
三、解答题
18.某直三棱柱零件如图①所示,张师傅根据此零件按的比例画出准确的三视图(如图②).已知在中,,又知.求:
(1)的长;
(2)这个直三棱柱的体积.
19.如图是由一些棱长均为1个单位长度的小正方体组合成的简单几何体.
(1)画该几何体的主视图、左视图:
(2)若给该几何体露在外面的面(不含底图)都喷上红漆,则需要喷漆的面积是 ;
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,则最多可以再添加 块小正方体.
20.某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:)
21.如果一个几何体从正面看、左面看、上面看看到的平面图形都是正方形,那么这个几何体可能是什么形状?
22.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将从正面、左面和上面看到的形状图画了出来(如图所示),则这堆正方体货箱共有多少箱?
23.如图是空心圆柱的两种视图,哪个有错误?为什么?
24.根据要求画出下列立体图形的视图.
《29.2三视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D A D A A A B
题号 11 12
答案 B B
1.B
【详解】分析:根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形进行分析.
详解:四棱锥的主视图与俯视图不同.
故选B.
点睛:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表示在三视图中.
2.A
【分析】本题考查了几何体的三视图,熟练掌握该知识点是解题的关键.根据三视图进行判断即可.
【详解】解:由三视图(主视图、左视图、俯视图)可知这个几何体的形状如下:
故选:A.
3.D
【分析】根据主视图即可判断出D为错误选项.
【详解】由D选项的主视图与图形的主视图不符
即可判断D为错误选项;
故选D.
【点睛】本题考查由三视图判断几何体,熟练掌握几何体的三视图的相关知识是解题关键.
4.D
【详解】根据左视图,正视图,俯视图的画法分别画出图形,钢管的左视图和正视图都是一个矩形,并且中间一个小矩形,小矩形的边是虚线,它的俯视图是两个圆,都是实线.
点睛:本题考查简单组合体的三视图的画法,主要培养学生的空间想象能力和动手操作能力.
5.A
【分析】根据三视图的特点,左视图从图形的左边向右看,看到一个正方形的面,在面上有一条实线,得到结果.
【详解】左视图从图形的左边向右看,看到一个正方形的面,在面上有一条实线,故选A.
【点睛】本题考查了三视图的定义,熟练掌握该定义可求解.
6.D
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形和圆心可判断出这个几何体应该是圆锥,
故选:D.
【点睛】本题考查由三视图判断几何体.
7.A
【详解】分析】直接利用左视图以及俯视图进而分析得出答案.
详解:由左视图可得,第2层上至少一个小立方体,
第1层一共有5个小立方体,故小正方体的个数最少为:6个,故小正方体的个数不可能是5个.
故选A.
点睛:此题主要考查了由三视图判断几何体,正确想象出最少时几何体的形状是解题关键.
8.A
【分析】找到从上面看所得到的图形即可.
【详解】解:从物体上面看,它的俯视图是
故选:A.
【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.
9.A
【详解】试题分析:根据几何体的三视图可以得到该几何体是圆柱,圆柱的侧面展开图是矩形,且高度=主视图的高,宽度=俯视图的周长.
故选A.
考点:1、由三视图判断几何体;2、几何体的展开图
10.B
【分析】依次观察各建筑物的图片即可作出判断,注意所有的看到的棱都应表现在主视图中.
【详解】解:最符合视图特点的建筑物的图片是选项B所示图片.
故选:B.
【点睛】本题考查三视图的知识,主视图是从物体的正面看得到的视图.
11.B
【分析】根据简单几何体的三视图即可判断.
【详解】由图形可知,主视图为
故选B.
【点睛】此题主要考查三视图的判断,解题的关键是熟知三视图的判断方法.
12.B
【分析】本题考查几何体的三视图画法.由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,1;据此可画出图形.
【详解】解:如图所示:
故选:B.
13.18 cm2
【分析】该几何体露在外面的部分是两个正视图,两个侧视图,一个俯视图面积的和,进而求得答案.
【详解】该几何体露在外面的部分是两个正视图,两个侧视图,一个俯视图面积和,
即.
【点睛】本题考查了几何体三视图和空间想象能力,熟练掌握三视图定义和充分发挥空间想象力是解题关键.
14. 俯视图 主视图 左视图
【详解】第一幅图是从上面看到的图形,是俯视图;第二幅图是从正面看到的图形,是主视图;第三幅图是从左面看到的图形,是左视图.
15.
【分析】分别画出这个几何体的三视图,然后根据轴对称图形的定义结合概率计算公式求解即可.
【详解】解:如图所示,该几何体的三视图为:
由三视图可知只有从上面看和从左面看的图形是轴对称图形,
∴抽取的视图是轴对称图形的概率为,
故答案为:.
【点睛】本题主要考查了简单几何组合体的三视图,轴对称图形的定义,简单的概率计算,正确画出三视图是解题的关键.
16.4个.
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从左视图可看出每一行小正方体的层数和个数,从而算出总的个数.
【详解】解:从俯视图上看,此几何体的下面有3个小正方体,
从左视图和主视图上看,最.上面有1个小正方体,
故组成这个几何体的小立方块的个数是:3+1=4.
故答案为: 4.
【点睛】此题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
17.
【详解】试题分析:由几何体的主视图和左视图都是等腰三角形,俯视图是圆,可以判断这个工件的几何体是圆锥.由等腰三角形的高为3,底面半径为1,可计算弧长,再根据圆锥侧面面积S=πrl计算.
试题解析:如图:
∵AO=3,CO=1,
∴AC=.
⊙O周长为2π.
∴此工件侧面积为.
考点:1.圆锥的计算;2.由三视图判断几何体.
18.(1)厘米
(2)立方厘米
【分析】本题考查了等腰直角三角形的判定与性质、勾股定理、三棱柱的三视图及三棱柱的体积计算:
(1)过点E作于点H,则根据题意可得出,然后由勾股定理计算即可得出答案;
(2)根据三棱柱的体积等于底面积乘以棱柱的高进行计算即可.
【详解】(1)解:过点E作于点H,如图.
在中,,
∴.
∴.
∴由勾股定理,得,
∴.
由图形可知.
(2)解:直三棱柱的体积.
19.(1)见详解;
(2)27;
(3)3.
【分析】(1)根据三视图的概念求解可得;
(2)将主视图、左视图分别乘2的面积,加上俯视图的面积即可得解;
(3)若使该几何体主视图和左视图不变,只可在底层添加方块,可以添加3块小正方体.
【详解】(1)如图所示:
(2)解:(7×2+4×2)×(1×1)+5×(1×1)
=14+8+5
=27
故答案为:27.
(3)若使该几何体主视图和左视图不变,可在最底层从右数第一至三列的第一行各添加一个,添加3块小正方体.
故答案为:3.
【点睛】本题主要考查了画三视图,解题的关键是掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都化成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方体的数目及位置.
20.每顶帐篷的表面积为96000πcm2.
【分析】根据三视图得到每顶帐篷由圆锥的侧面和圆柱的侧面组成,且圆锥的母线长为240cm,底面圆的半径为150cm,圆锥的高为200cm,由于圆锥的侧面展开图为一扇形,圆柱的侧面展开图为矩形,则根据扇形的面积公式和矩形的面积公式分别进行计算,然后求它们的和积.
【详解】解:根据三视图得圆锥的母线长为240cm,底面圆的半径为150cm,圆锥的高为200cm.
所以圆锥的侧面积= 2π 150 240=36000π,
圆柱的侧面积=2π 150 200=60000π,
所以每顶帐篷的表面积=36000π+60000π=96000π(cm2).
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.
21.正方体或正方体内部挖去一部分
【分析】由题意可知这个几何体不透明时,可能表面是正方体,而中间缺一部分.
【详解】由三视图是三个正方形可知,原立体图形应是四棱柱或挖去一部分的四棱柱.
因为正方形四边相等,四个角均为直角,可确定这个几何体是正方体.
【点睛】本题考查了正方体的三视图,从视图反过来考虑几何体,要注意考虑多种可能性,结合实物,亲自变换角度去观察,才能提高空间想象能力.
22.9箱
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】由题意可知,一共有三层正方体,
由俯视图可确定第一层有7个正方体
由主视图可知,第二层有1个正方体,第三层有1个正方体
即7+1+1=9(个)
故共有9箱正方体货箱.
【点睛】本题考查由三视图判断几何体,熟练掌握几何体的三视图的相关知识是解题关键.
23.(1)(2)是错误的,(3)是正确的,理由见解析.
【分析】分别找到从正面,从上面看所得到的图形即可,注意所有的棱都应表现在主视图和俯视图中.
【详解】如图所示,空心圆柱体的主视图是圆环;
俯视图是矩形,且有两条竖着的虚线.
∴(1)(2)是错误的,(3)是正确的
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
24.答案见解析.
【分析】根据主视图是从正面看到的图形,左视图是从左面看到的图形,俯视图是从上面看到的图形,即可得到结果.
【详解】解:如图所示:
【点睛】本题考查几何体的三视图,作图能力是学生必须具备的基本能力,因为此类问题在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
