3.9弧长及扇形的面积同步强化练习(含解析)
文档属性
| 名称 | 3.9弧长及扇形的面积同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
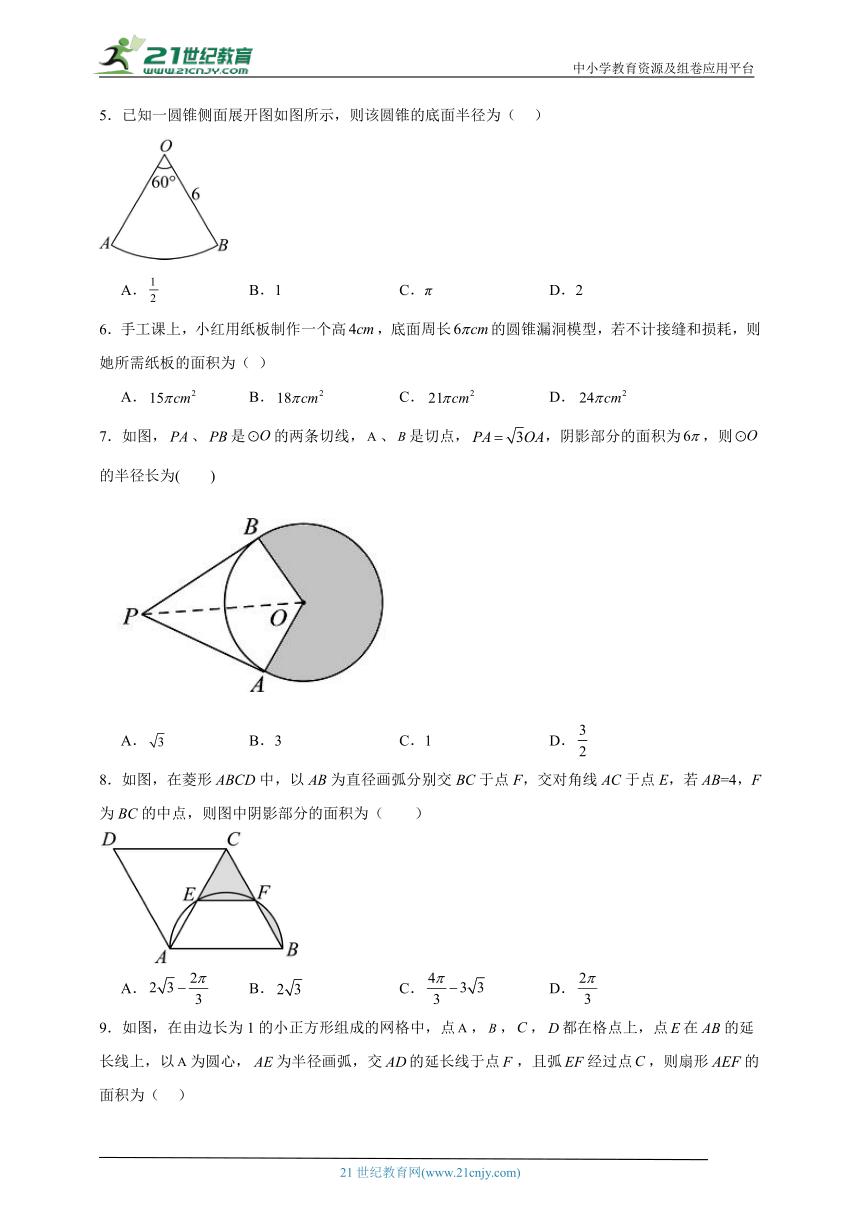
1.一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm B.10πcm C.5cm D.5πcm
2.若扇形的圆心角为45°,半径为6,则扇形的弧长为( )
A. B. C. D.
3.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B. C. D.
4.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
5.已知一圆锥侧面展开图如图所示,则该圆锥的底面半径为( )
A. B.1 C.π D.2
6.手工课上,小红用纸板制作一个高,底面周长的圆锥漏洞模型,若不计接缝和损耗,则她所需纸板的面积为( )
A. B. C. D.
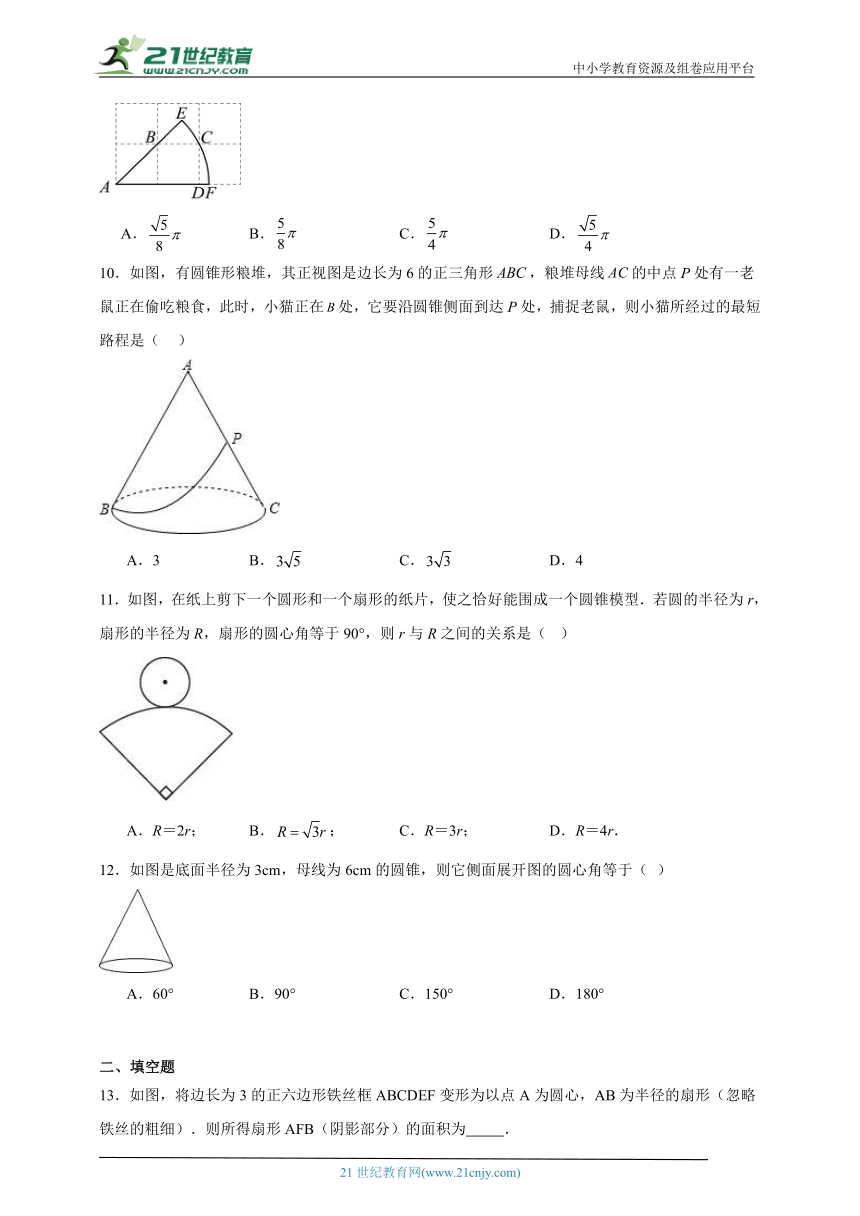
7.如图,、是的两条切线,、是切点,,阴影部分的面积为,则的半径长为( )
A. B.3 C.1 D.
8.如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,在由边长为1的小正方形组成的网格中,点,,,都在格点上,点在的延长线上,以为圆心,为半径画弧,交的延长线于点,且弧经过点,则扇形的面积为( )
A. B. C. D.
10.如图,有圆锥形粮堆,其正视图是边长为6的正三角形,粮堆母线的中点P处有一老鼠正在偷吃粮食,此时,小猫正在处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是( )
A.3 B. C. D.4
11.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
A.R=2r; B.; C.R=3r; D.R=4r.
12.如图是底面半径为3cm,母线为6cm的圆锥,则它侧面展开图的圆心角等于( )
A.60° B.90° C.150° D.180°
二、填空题
13.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
14.圆锥的母线长为,底面圆的周长为,那么这个圆锥的侧面展开图的圆心角的度数是 .
15.如图,点A,B,C,在半径为6的圆上,∠ACB=45°,则图中阴影部分的面积为 (结果保留).
16.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300π cm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.
17.已知圆锥的底面半径长为5,侧面展开后所得的扇形的圆心角为120°,则该圆锥的母线长等于 .
三、解答题
18.如图,中,.
(1)将绕点逆时针旋转,画出旋转后的三角形;
(2)若,,求点在旋转过程中所经过的路径长(结果保留).
19.如图,正三角形的边长为分别为的中点,以三点为圆心,长为半径作圆,求图中阴影部分的面积.
20.如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接.
(1)求证:;
(2)若⊙O的半径为3,,求的长(结果保留π).
21.如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,=1.4,=1.7).
22.如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕点O顺时针旋转180°,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C在旋转过程中经过的路径长.
23.如图:带阴影部分的半圆的面积是多少?(取3)
24.在数学实验课上,小莹将含角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如下示意图
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗?请说明理由.
《3.9弧长及扇形的面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A B A B D B B
题号 11 12
答案 D D
1.B
【分析】重物上升的高度等于A点绕圆心转东180度的弧长,然后根据弧长公式计算即可.
【详解】解:根据题意得,重物上升的高度= =10π(cm).
故选:B.
【点睛】本题考查了弧长的计算:弧长公式为 (弧长为l,圆心角度数为n,圆的半径为R).也考查了旋转的性质.
2.C
【分析】把已知数据代入弧长公式,计算即可.
【详解】解:该扇形的弧长=,
故选:C.
【点睛】本题考查的是弧长的计算,掌握弧长公式:是解题的关键.
3.D
【分析】先证明△ABD为等腰直角三角形得到∠ABD=45°,BD=AB,再证明△CBD为等边三角形得到BC=BD=AB,利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,从而得到下面圆锥的侧面积.
【详解】∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=AB,
∵∠ABC=105°,
∴∠CBD=60°,
而CB=CD,
∴△CBD为等边三角形,
∴BC=BD=AB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,
∴下面圆锥的侧面积=×1=.
故选D.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了等腰直角三角形和等边三角形的性质.
4.A
【分析】由底面圆的半径=5米,根据勾股定理求出母线长,利用圆锥的侧面面积公式,以及利用矩形的面积公式求得圆柱的侧面面积,最后求和.
【详解】解:∵底面半径=5米,圆锥高为2米,圆柱高为3米,
∴圆锥的母线长=米,
∴圆锥的侧面积=,
圆柱的侧面积=底面圆周长×圆柱高,
即,
故需要的毛毡:米,
故选:A.
【点睛】此题主要考查勾股定理,圆周长公式,圆锥侧面积,圆柱侧面积等,分别得出圆锥与圆柱侧面积是解题关键.
5.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据这个扇形的弧长等于圆锥底面的周长列方程即可.
【详解】解:依题意,
解得:
故选:B.
6.A
【分析】首先求得扇形的底面半径长,然后利用勾股定理求得圆锥的母线长,最后利用扇形的面积公式即可求解.
【详解】解:设底面半径是r,则,
解得:r=3,
则母线长是:,
则她所需纸板的面积是:.
所以A选项是正确的.
【点睛】本题主要考查圆锥的基本知识,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
7.B
【分析】连接,根据切线的性质得到,根据已知条件得到,根据扇形的面积公式即可得到结论.
【详解】解:连接,
∵、是的两条切线,
∴,
∵,
∴,
∴,
∵阴影部分的面积为,
∴
∴
故选:B.
【点睛】本题考查了切线的性质,扇形的面积公式,三角函数的定义,熟练掌握切线的性质是解题的关键.
8.D
【分析】取AB的中点O,连接AF,OF,先证明△ABC是等边三角形,再把问题转化为S阴=S扇形OBF,由此即可解决问题.
【详解】解:如图,取AB的中点O,连接AF,OF.
∵AB是直径,
∴∠AFB=90°,
∴AF⊥BF,∵CF=BF,
∴AC=AB,
∵四边形ABCD是菱形,
∴AB=BC=AC,
∴△ABC是等边三角形,
∴AE=EC,
易证△CEF≌△BOF,
∴S阴=S扇形OBF==,
故选D.
【点睛】考查扇形的面积,菱形的性质,等边三角形的判定和性质等知识,解题的关键是学会用转化的思想思考问题.
9.B
【分析】连接AC,根据网格的特点求出r=AC的长度,再得到扇形的圆心角度数,根据扇形面积公式即可求解.
【详解】连接AC,则r=AC=
扇形的圆心角度数为∠BAD=45°,
∴扇形的面积==
故选B.
【点睛】此题主要考查扇形面积求解,解题的关键是熟知勾股定理及扇形面积公式.
10.B
【分析】求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为的等边三角形可知,展开图是半径是6的半圆.点是半圆的一个端点,而点是平分半圆的半径的中点,根据勾股定理就可求出两点和在展开图中的距离,就是这只小猫经过的最短距离.
【详解】
解:圆锥的底面周长是,则,
,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中,,度.
在圆锥侧面展开图中.
故小猫经过的最短距离是.故选:.
【点睛】
本题考查的是平面展开最短路线问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.
11.D
【详解】解:扇形的弧长是:,
圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:
∴即:R=4r,
r与R之间的关系是R=4r.
故选D.
12.D
【分析】圆锥的底面周长,就是圆锥的侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图的角度,把相关数值代入即可求解.
【详解】∵底面半径为3cm
所以圆锥的底面周长为6πcm;
设圆心角的度数是n度.则
,
解得:n=180.
故选D.
【点睛】此题主要考查了圆锥的有关计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
13.18
【详解】解:∵正六边形ABCDEF的边长为3,
∴AB=BC=CD=DE=EF=FA=3,
∴弧BAF的长=3×6﹣3﹣3═12,
∴扇形AFB(阴影部分)的面积=×12×3=18.
故答案为18.
【点睛】本题考查正多边形和圆;扇形面积的计算.
14.°
【分析】根据圆锥的侧面展开图扇形的弧长等于圆锥底面的周长列式计算即可.
【详解】解:设这个圆锥的侧面展开图的圆心角为n°,
根据题意得,6=,
解得,n=120,
∴这个圆锥的侧面展开图的圆心角度数为120°,
故答案为:120°.
【点睛】本题考查的是圆锥的计算,掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键.
15.9π-18/-18+9π
【分析】根据圆周角定理求出∠BOA,根据扇形面积公式计算即可.
【详解】解:连接OA、OB,
由圆周角定理得,∠BOA=2∠ACB=90°,
∴△BOA为等腰直角三角形,
则图中阴影部分的面积= -×6×6=9π-18,
故答案为:9π-18.
【点睛】本题考查的是扇形面积计算、圆周角定理,掌握扇形面积公式是解题的关键.
16.20
【详解】【分析】根据扇形面积公式先求出半径AB,再根据BD=2AD,求出BD.
【详解】由已得,
解得r=30,即AB=30cm
因为,BD=2AD,BD+AD=AB
所以,BD=20cm,
故答案为:20
【点睛】本题考核知识点:扇形面积.解题关键点:熟记扇形面积公式.
17.15
【分析】根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得.
【详解】解:设圆锥的母线长为R,
由题意得,
解得:R=15.
故答案为:15.
【点睛】主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
18.(1)见解析
(2)
【分析】本题考查了旋转作图,勾股定理,弧长的计算,熟练掌握以上知识点是解题的关键.
(1)分别作出、点绕点逆时针旋转的对应点,依次连接即可;
(2)根据勾股定理求得,再根据弧长公式计算即可.
【详解】(1)解:分别作出、点绕点逆时针旋转的对应点、,依次连接,
如图所示,即为所求:
(2)解:如(1)图,
,,
故点在旋转过程中所经过的路径长.
19.a2-
【分析】如图,连接证明 再求解 再求解的面积与扇形面积,从而可得答案.
【详解】解:如图,连接
正三角形的边长为分别为的中点,
S△ABC=a=a2,
S扇形FBD=×π()2=×=,
∴S阴影= S△ABC-3S扇形FBD=a2-3×=a2-.
【点睛】本题考查的是等边三角形的性质,圆的基本性质,扇形面积的计算,掌握等边三角形面积的计算与扇形面积的计算是解题的关键.
20.(1)证明见解析;
(2)
【分析】(1)根据已知条件可证明四边形是平行四边形,由平行四边形的性质可得,等量代换可得,即可得出答案;
(2)连接,由(1)中结论可计算出的度数,根据圆周角定理可计算出的度数,再根据弧长计算公式计算即可得出答案.
【详解】(1)证明:∵,,
∴四边形为平行四边形,
∴,
∵,
∴,
∴.
(2)解:连接,如图,
由(1)得,
∵,
∴,
∴的长.
【点睛】本题主要考查了等腰三角形的判定与性质,平行四边形的判定与性质,圆的性质与弧长公式,考查化归与转化思想,推理能力,几何直观等数学素养.
21.(1)证明见解析;(2)26.5.
【分析】(1)根据平行线的性质和等腰三角形的性质可得∠CDA=∠DAO,∠DAO=∠ADO,即可证得结论;
(2)易证∠CDA=∠BAD=∠CAD,可得,再证明∠DOB=60°,即可得△BOD是等边三角形,由此即可解决问题.
【详解】解:(1)∵CD∥AB,
∴∠CDA=∠BAD,
又∵OA=OD,
∴∠ADO=∠BAD,
∴∠ADO=∠CDA,
∴DA平分∠CDO.
(2)如图,连接BD,
∵AB是直径,
∴∠ADB=90°,
∵AC=CD,
∴∠CAD=∠CDA,
又∵CD∥AB,
∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,
∴,
又∵∠AOB=180°,
∴∠DOB=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=AB=6,
∵,
∴AC=BD=6,
∵BE切⊙O于B,
∴BE⊥AB,
∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,
∴BE⊥CE,
∴DE=BD=3,BE=BD×cos∠DBE=6×=3,
∴的长==2π,
∴图中阴影部分周长之和为2π+6+2π+3+3=4π+9+3=4×3.1+9+3×1.7=26.5.
【点睛】本题考查切线的性质;弧长的计算.
22.(1)详见解析;(2)π
【分析】(1)连接BO、CO、并延长相同单位找到对应点,顺次连接即可.
(2)点C旋转过程所经过的路径是一段弧线,根据弧长公式即可计算.
【详解】(1)旋转后的图形如图所示.
(2)如图,连接OC.
由题意可知,点C的旋转路径是以O为圆心,OC的长为半径的半圆.
∵OC,∴点C在旋转过程中经过的路径长为l.
【点睛】本题综合考查了旋转变换作图和弧长公式的计算方法.
23.37.5
【分析】先根据勾股定理求出半圆的直径,再根据圆的面积公式求出半圆的面积即可.
【详解】根据勾股定理,求出半圆的直径==10,
则半圆的半径为5,
所以半圆的面积为π×52=37.5.
故答案为37.5.
【点睛】本题主要考查了勾股定理与圆的面积公式,求出圆直径的长度是解答的关键.
24.不认同,理由见详解
【分析】根据圆锥的侧面面积公式进行比较即可得到答案.
【详解】解:甲圆锥的底面半径为BC,母线为AB,,
乙圆锥的底面半径为AC,母线为AB,,
∵,
∴,
故不认同小亮的说法.
【点睛】本题考查圆锥的侧面面积,解题的关键是熟知圆锥侧面面积的计算公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm B.10πcm C.5cm D.5πcm
2.若扇形的圆心角为45°,半径为6,则扇形的弧长为( )
A. B. C. D.
3.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B. C. D.
4.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
5.已知一圆锥侧面展开图如图所示,则该圆锥的底面半径为( )
A. B.1 C.π D.2
6.手工课上,小红用纸板制作一个高,底面周长的圆锥漏洞模型,若不计接缝和损耗,则她所需纸板的面积为( )
A. B. C. D.
7.如图,、是的两条切线,、是切点,,阴影部分的面积为,则的半径长为( )
A. B.3 C.1 D.
8.如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,在由边长为1的小正方形组成的网格中,点,,,都在格点上,点在的延长线上,以为圆心,为半径画弧,交的延长线于点,且弧经过点,则扇形的面积为( )
A. B. C. D.
10.如图,有圆锥形粮堆,其正视图是边长为6的正三角形,粮堆母线的中点P处有一老鼠正在偷吃粮食,此时,小猫正在处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是( )
A.3 B. C. D.4
11.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
A.R=2r; B.; C.R=3r; D.R=4r.
12.如图是底面半径为3cm,母线为6cm的圆锥,则它侧面展开图的圆心角等于( )
A.60° B.90° C.150° D.180°
二、填空题
13.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
14.圆锥的母线长为,底面圆的周长为,那么这个圆锥的侧面展开图的圆心角的度数是 .
15.如图,点A,B,C,在半径为6的圆上,∠ACB=45°,则图中阴影部分的面积为 (结果保留).
16.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300π cm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.
17.已知圆锥的底面半径长为5,侧面展开后所得的扇形的圆心角为120°,则该圆锥的母线长等于 .
三、解答题
18.如图,中,.
(1)将绕点逆时针旋转,画出旋转后的三角形;
(2)若,,求点在旋转过程中所经过的路径长(结果保留).
19.如图,正三角形的边长为分别为的中点,以三点为圆心,长为半径作圆,求图中阴影部分的面积.
20.如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接.
(1)求证:;
(2)若⊙O的半径为3,,求的长(结果保留π).
21.如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,=1.4,=1.7).
22.如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕点O顺时针旋转180°,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C在旋转过程中经过的路径长.
23.如图:带阴影部分的半圆的面积是多少?(取3)
24.在数学实验课上,小莹将含角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如下示意图
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗?请说明理由.
《3.9弧长及扇形的面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A B A B D B B
题号 11 12
答案 D D
1.B
【分析】重物上升的高度等于A点绕圆心转东180度的弧长,然后根据弧长公式计算即可.
【详解】解:根据题意得,重物上升的高度= =10π(cm).
故选:B.
【点睛】本题考查了弧长的计算:弧长公式为 (弧长为l,圆心角度数为n,圆的半径为R).也考查了旋转的性质.
2.C
【分析】把已知数据代入弧长公式,计算即可.
【详解】解:该扇形的弧长=,
故选:C.
【点睛】本题考查的是弧长的计算,掌握弧长公式:是解题的关键.
3.D
【分析】先证明△ABD为等腰直角三角形得到∠ABD=45°,BD=AB,再证明△CBD为等边三角形得到BC=BD=AB,利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,从而得到下面圆锥的侧面积.
【详解】∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=AB,
∵∠ABC=105°,
∴∠CBD=60°,
而CB=CD,
∴△CBD为等边三角形,
∴BC=BD=AB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,
∴下面圆锥的侧面积=×1=.
故选D.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了等腰直角三角形和等边三角形的性质.
4.A
【分析】由底面圆的半径=5米,根据勾股定理求出母线长,利用圆锥的侧面面积公式,以及利用矩形的面积公式求得圆柱的侧面面积,最后求和.
【详解】解:∵底面半径=5米,圆锥高为2米,圆柱高为3米,
∴圆锥的母线长=米,
∴圆锥的侧面积=,
圆柱的侧面积=底面圆周长×圆柱高,
即,
故需要的毛毡:米,
故选:A.
【点睛】此题主要考查勾股定理,圆周长公式,圆锥侧面积,圆柱侧面积等,分别得出圆锥与圆柱侧面积是解题关键.
5.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据这个扇形的弧长等于圆锥底面的周长列方程即可.
【详解】解:依题意,
解得:
故选:B.
6.A
【分析】首先求得扇形的底面半径长,然后利用勾股定理求得圆锥的母线长,最后利用扇形的面积公式即可求解.
【详解】解:设底面半径是r,则,
解得:r=3,
则母线长是:,
则她所需纸板的面积是:.
所以A选项是正确的.
【点睛】本题主要考查圆锥的基本知识,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
7.B
【分析】连接,根据切线的性质得到,根据已知条件得到,根据扇形的面积公式即可得到结论.
【详解】解:连接,
∵、是的两条切线,
∴,
∵,
∴,
∴,
∵阴影部分的面积为,
∴
∴
故选:B.
【点睛】本题考查了切线的性质,扇形的面积公式,三角函数的定义,熟练掌握切线的性质是解题的关键.
8.D
【分析】取AB的中点O,连接AF,OF,先证明△ABC是等边三角形,再把问题转化为S阴=S扇形OBF,由此即可解决问题.
【详解】解:如图,取AB的中点O,连接AF,OF.
∵AB是直径,
∴∠AFB=90°,
∴AF⊥BF,∵CF=BF,
∴AC=AB,
∵四边形ABCD是菱形,
∴AB=BC=AC,
∴△ABC是等边三角形,
∴AE=EC,
易证△CEF≌△BOF,
∴S阴=S扇形OBF==,
故选D.
【点睛】考查扇形的面积,菱形的性质,等边三角形的判定和性质等知识,解题的关键是学会用转化的思想思考问题.
9.B
【分析】连接AC,根据网格的特点求出r=AC的长度,再得到扇形的圆心角度数,根据扇形面积公式即可求解.
【详解】连接AC,则r=AC=
扇形的圆心角度数为∠BAD=45°,
∴扇形的面积==
故选B.
【点睛】此题主要考查扇形面积求解,解题的关键是熟知勾股定理及扇形面积公式.
10.B
【分析】求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为的等边三角形可知,展开图是半径是6的半圆.点是半圆的一个端点,而点是平分半圆的半径的中点,根据勾股定理就可求出两点和在展开图中的距离,就是这只小猫经过的最短距离.
【详解】
解:圆锥的底面周长是,则,
,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中,,度.
在圆锥侧面展开图中.
故小猫经过的最短距离是.故选:.
【点睛】
本题考查的是平面展开最短路线问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.
11.D
【详解】解:扇形的弧长是:,
圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:
∴即:R=4r,
r与R之间的关系是R=4r.
故选D.
12.D
【分析】圆锥的底面周长,就是圆锥的侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图的角度,把相关数值代入即可求解.
【详解】∵底面半径为3cm
所以圆锥的底面周长为6πcm;
设圆心角的度数是n度.则
,
解得:n=180.
故选D.
【点睛】此题主要考查了圆锥的有关计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
13.18
【详解】解:∵正六边形ABCDEF的边长为3,
∴AB=BC=CD=DE=EF=FA=3,
∴弧BAF的长=3×6﹣3﹣3═12,
∴扇形AFB(阴影部分)的面积=×12×3=18.
故答案为18.
【点睛】本题考查正多边形和圆;扇形面积的计算.
14.°
【分析】根据圆锥的侧面展开图扇形的弧长等于圆锥底面的周长列式计算即可.
【详解】解:设这个圆锥的侧面展开图的圆心角为n°,
根据题意得,6=,
解得,n=120,
∴这个圆锥的侧面展开图的圆心角度数为120°,
故答案为:120°.
【点睛】本题考查的是圆锥的计算,掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键.
15.9π-18/-18+9π
【分析】根据圆周角定理求出∠BOA,根据扇形面积公式计算即可.
【详解】解:连接OA、OB,
由圆周角定理得,∠BOA=2∠ACB=90°,
∴△BOA为等腰直角三角形,
则图中阴影部分的面积= -×6×6=9π-18,
故答案为:9π-18.
【点睛】本题考查的是扇形面积计算、圆周角定理,掌握扇形面积公式是解题的关键.
16.20
【详解】【分析】根据扇形面积公式先求出半径AB,再根据BD=2AD,求出BD.
【详解】由已得,
解得r=30,即AB=30cm
因为,BD=2AD,BD+AD=AB
所以,BD=20cm,
故答案为:20
【点睛】本题考核知识点:扇形面积.解题关键点:熟记扇形面积公式.
17.15
【分析】根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得.
【详解】解:设圆锥的母线长为R,
由题意得,
解得:R=15.
故答案为:15.
【点睛】主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
18.(1)见解析
(2)
【分析】本题考查了旋转作图,勾股定理,弧长的计算,熟练掌握以上知识点是解题的关键.
(1)分别作出、点绕点逆时针旋转的对应点,依次连接即可;
(2)根据勾股定理求得,再根据弧长公式计算即可.
【详解】(1)解:分别作出、点绕点逆时针旋转的对应点、,依次连接,
如图所示,即为所求:
(2)解:如(1)图,
,,
故点在旋转过程中所经过的路径长.
19.a2-
【分析】如图,连接证明 再求解 再求解的面积与扇形面积,从而可得答案.
【详解】解:如图,连接
正三角形的边长为分别为的中点,
S△ABC=a=a2,
S扇形FBD=×π()2=×=,
∴S阴影= S△ABC-3S扇形FBD=a2-3×=a2-.
【点睛】本题考查的是等边三角形的性质,圆的基本性质,扇形面积的计算,掌握等边三角形面积的计算与扇形面积的计算是解题的关键.
20.(1)证明见解析;
(2)
【分析】(1)根据已知条件可证明四边形是平行四边形,由平行四边形的性质可得,等量代换可得,即可得出答案;
(2)连接,由(1)中结论可计算出的度数,根据圆周角定理可计算出的度数,再根据弧长计算公式计算即可得出答案.
【详解】(1)证明:∵,,
∴四边形为平行四边形,
∴,
∵,
∴,
∴.
(2)解:连接,如图,
由(1)得,
∵,
∴,
∴的长.
【点睛】本题主要考查了等腰三角形的判定与性质,平行四边形的判定与性质,圆的性质与弧长公式,考查化归与转化思想,推理能力,几何直观等数学素养.
21.(1)证明见解析;(2)26.5.
【分析】(1)根据平行线的性质和等腰三角形的性质可得∠CDA=∠DAO,∠DAO=∠ADO,即可证得结论;
(2)易证∠CDA=∠BAD=∠CAD,可得,再证明∠DOB=60°,即可得△BOD是等边三角形,由此即可解决问题.
【详解】解:(1)∵CD∥AB,
∴∠CDA=∠BAD,
又∵OA=OD,
∴∠ADO=∠BAD,
∴∠ADO=∠CDA,
∴DA平分∠CDO.
(2)如图,连接BD,
∵AB是直径,
∴∠ADB=90°,
∵AC=CD,
∴∠CAD=∠CDA,
又∵CD∥AB,
∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,
∴,
又∵∠AOB=180°,
∴∠DOB=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=AB=6,
∵,
∴AC=BD=6,
∵BE切⊙O于B,
∴BE⊥AB,
∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,
∴BE⊥CE,
∴DE=BD=3,BE=BD×cos∠DBE=6×=3,
∴的长==2π,
∴图中阴影部分周长之和为2π+6+2π+3+3=4π+9+3=4×3.1+9+3×1.7=26.5.
【点睛】本题考查切线的性质;弧长的计算.
22.(1)详见解析;(2)π
【分析】(1)连接BO、CO、并延长相同单位找到对应点,顺次连接即可.
(2)点C旋转过程所经过的路径是一段弧线,根据弧长公式即可计算.
【详解】(1)旋转后的图形如图所示.
(2)如图,连接OC.
由题意可知,点C的旋转路径是以O为圆心,OC的长为半径的半圆.
∵OC,∴点C在旋转过程中经过的路径长为l.
【点睛】本题综合考查了旋转变换作图和弧长公式的计算方法.
23.37.5
【分析】先根据勾股定理求出半圆的直径,再根据圆的面积公式求出半圆的面积即可.
【详解】根据勾股定理,求出半圆的直径==10,
则半圆的半径为5,
所以半圆的面积为π×52=37.5.
故答案为37.5.
【点睛】本题主要考查了勾股定理与圆的面积公式,求出圆直径的长度是解答的关键.
24.不认同,理由见详解
【分析】根据圆锥的侧面面积公式进行比较即可得到答案.
【详解】解:甲圆锥的底面半径为BC,母线为AB,,
乙圆锥的底面半径为AC,母线为AB,,
∵,
∴,
故不认同小亮的说法.
【点睛】本题考查圆锥的侧面面积,解题的关键是熟知圆锥侧面面积的计算公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
