第一章直角三角形的边角关系同步强化练习(含解析)
文档属性
| 名称 | 第一章直角三角形的边角关系同步强化练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 18:52:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章直角三角形的边角关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为( )
A. B. C. D.
2.如图,在菱形中,,,,则tan∠的值是( )
A. B.2 C. D.
3.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为( )
A.100米 B.110米 C.120米 D.130米
4.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1:,坝外斜坡的坡度i=1:1,则两个坡角的和为( )
A.90° B.60° C.75° D.105°
5.如图,王亮为了测量一条河流的宽度,他在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽(的长)可以表示为( )
A.米 B.米
C.米 D.米
6.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A.b=atanB B.a=ccosB C.c= D.a=bcosA
7.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
8.如图,在高为h的山顶上,测得一建筑物顶端与底部的俯角分别为30°和60°,用h表示这个建筑物的高度为( )
A.h B.h C.h D.h
9.如图,已知的边,直线的方程为,则( )
A. B. C. D.
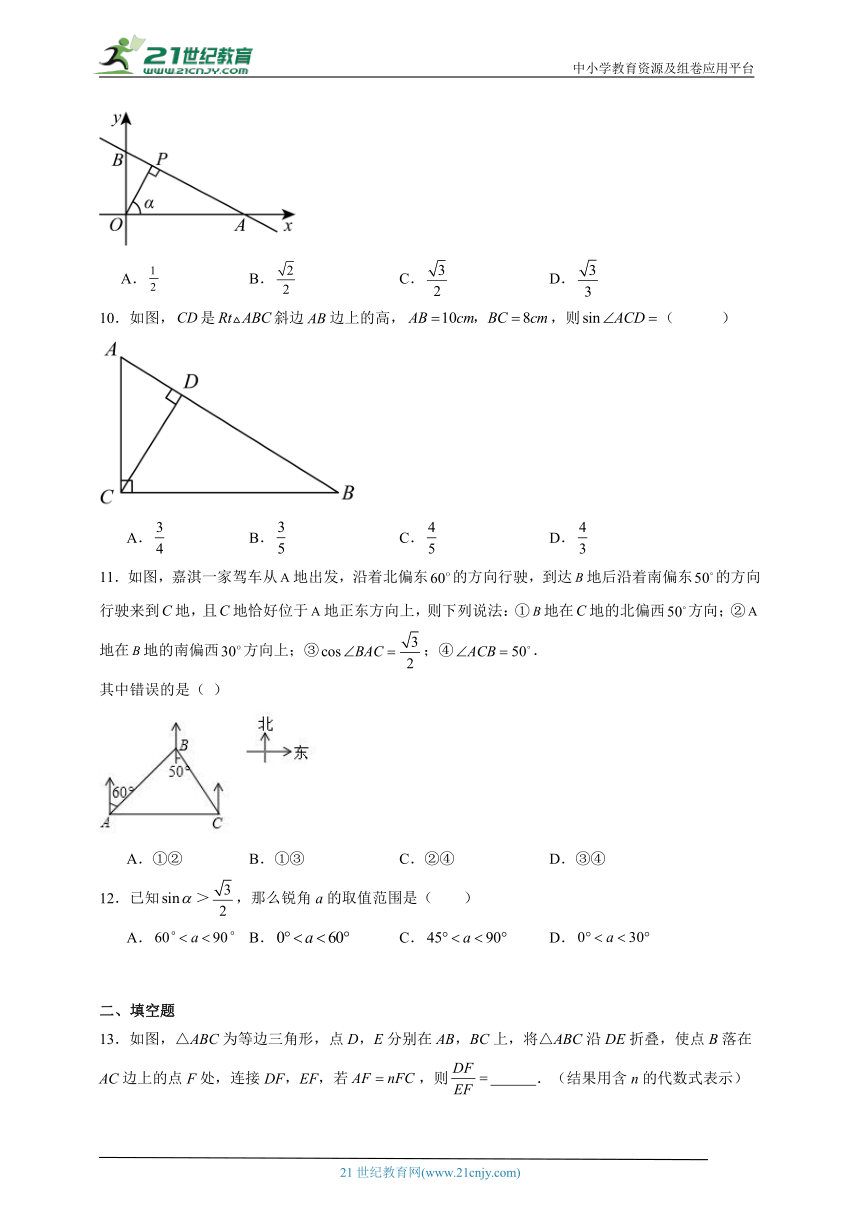
10.如图,是斜边边上的高,,则( )
A. B. C. D.
11.如图,嘉淇一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法:①地在地的北偏西方向;②地在地的南偏西方向上;③;④.
其中错误的是( )
A.①② B.①③ C.②④ D.③④
12.已知>,那么锐角a的取值范围是( )
A. B. C. D.
二、填空题
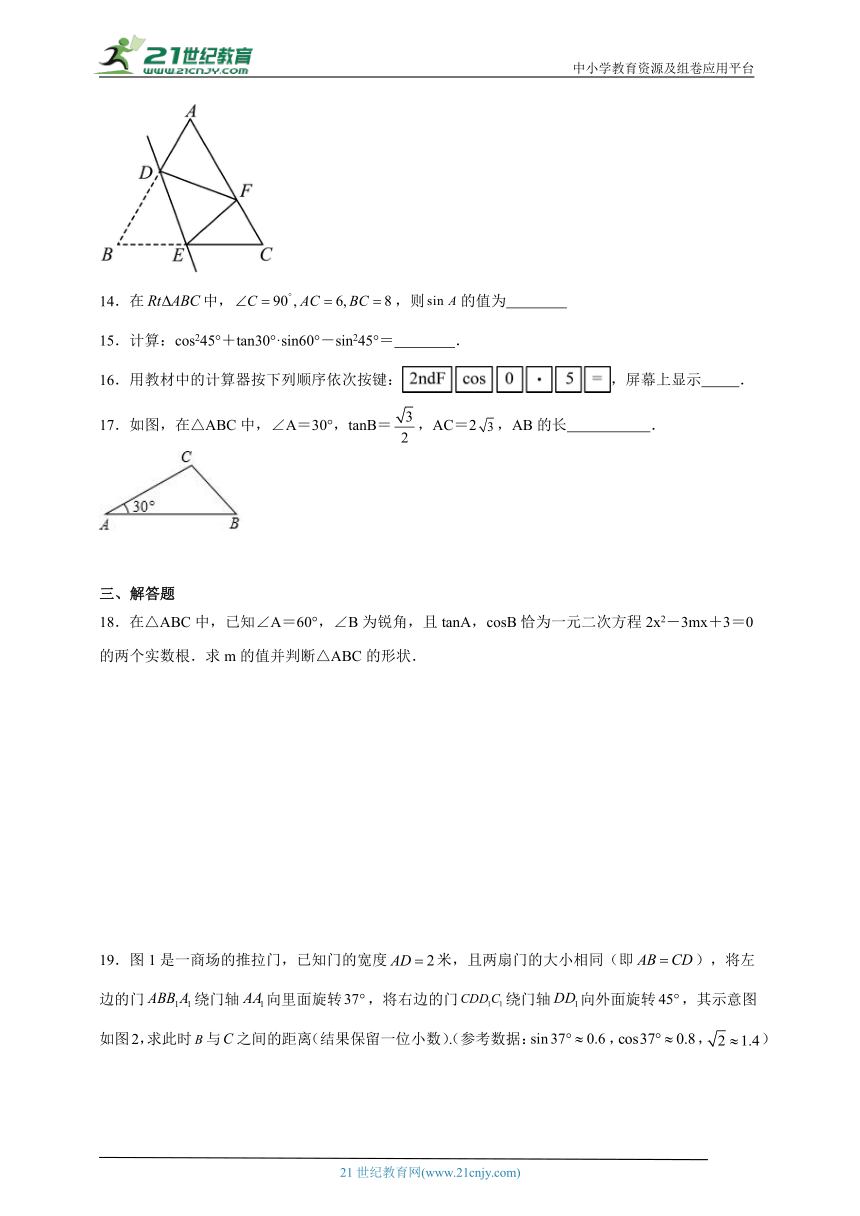
13.如图,△ABC为等边三角形,点D,E分别在AB,BC上,将△ABC沿DE折叠,使点B落在AC边上的点F处,连接DF,EF,若,则 .(结果用含n的代数式表示)
14.在中,,则的值为
15.计算:cos245°+tan30°·sin60°-sin245°= .
16.用教材中的计算器按下列顺序依次按键:,屏幕上显示 .
17.如图,在△ABC中,∠A=30°,tanB=,AC=2,AB的长 .
三、解答题
18.在△ABC中,已知∠A=60°,∠B为锐角,且tanA,cosB恰为一元二次方程2x2-3mx+3=0的两个实数根.求m的值并判断△ABC的形状.
19.图1是一商场的推拉门,已知门的宽度米,且两扇门的大小相同(即),将左边的门绕门轴向里面旋转,将右边的门绕门轴向外面旋转,其示意图如图2,求此时与之间的距离(结果保留一位小数).(参考数据:,,)
20.周末,小红和小宇相约一起去郊外劳动基地参加劳动.已知小红家B在小宇家A的北偏西方向上,.两人到达劳动基地C处后,发现小宇家A在劳动基地C的南偏西方向上,小红家B在劳动基地C的南偏西方向上.求小宇家A到劳动基地C的距离.(结果保留1位小数;参考数据:,,,)
21.计算:
(1);
(2).
22.如图,在中,,,于点D.
(1)求的值;
(2)求的长.
23.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a=8,∠B=60°;
(2)在Rt△ABC中,∠C=90°,∠A=45°,b=.
24.如图,是等腰三角形,你能根据图中所给数据求出吗?
《第一章直角三角形的边角关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D C A D A A A B
题号 11 12
答案 C A
1.C
【分析】设与交于点E.由于阴影部分的面积,又,所以关键是求.为此,连接.根据易证,得出.在直角中,由正切的定义得出.再利用三角形的面积公式求出.
【详解】解:设与交于点E,连接.
在与中,,
,
∴(),
∴.
∵,
∴,
∴.
∴.
∴阴影部分的面积.
故选:C.
【点睛】本题主要考查了正方形、旋转的性质,直角三角形的判定及性质,图形的面积以及三角函数等知识,综合性较强,有一定难度.
2.B
【详解】解:设则
又因为在菱形ABCD中,
所以
,
由勾股定理知,
故答案为:B.
3.D
【分析】直接利用坡比的定义得出AC的长,再利用勾股定理得出AB的长.
【详解】解:∵某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,
∴=,
则=,
解得:AC=120米,
故AB===130(米).
故选:D.
【点睛】此题主要考查了解直角三角形的应用,正确掌握坡比的定义是解题关键.
4.C
【详解】解:如图所示,
∵ED:AE=1:,
∴∠A=30°.
∵CF:BF=1:1,
∴∠B=45°.
∴∠A+∠B=30°+45°=75°.
故选C.
【点睛】在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是这一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.
5.A
【分析】在中,利用的长,以及的度数,进而得到的度数,根据三角函数即可求得的长.
【详解】解:在中,
∵,,
∴,
∴,
∴,
即河宽米,
故选:A.
【点睛】此题考查了解直角三角形的应用-方向角问题,掌握方向角与正切函数的定义是解题的关键.
6.D
【详解】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
7.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
【点睛】本题主要考查了勾股定理,等腰直角三角形的性质,解直角三角形,熟练解直角三角形是解题的关键.
8.A
【分析】作CE⊥AB,根据∠DAB可以求得CE的长,根据CE即可求得AE的长,根据CD=BE=AB-AE即可解题.
【详解】解:作CE⊥AB,
∵∠DAB=90°-60°=30°,tan30°=
∴CE=BD=
∵∠ACE=30°,
∴AE=CEtan30°=
∴CD=BE=AB-AE==
故答案为.
【点睛】本题考查了特殊角的三角函数值,考查了直角三角形中三角函数的运用,本题中求得BD的长是解题的关键
9.A
【分析】本题考查了三角函数的定义和一次函数、勾股定理的知识,利用等角的代换,体现了思维的灵活性.根据一次函数的性质,求出点A、B的坐标,得到、的长度,再根据三角函数的定义即可求出的值.
【详解】直线的方程为
当时,;当时,,
∴,
∴
,
∵,
∴,
∵,
∴
∴
∴,
.
故选:A.
10.B
【分析】本题考查求锐角三角函数,勾股定理,
根据勾股定理先求出,再证明,进而即可求解
【详解】解:在中,
∵在和中,
,
故选B.
11.C
【分析】根据方位角及锐角三角函数的知识可以解得正确答案.
【详解】解:由题意可得如下标有角度的方位图,
∴B地在C地的北偏西 50°方向,①正确;A地在B地的南偏西 60°方向,②错误;
cos∠BAC=,③正确;∠ACB=90°-50°=40°,④错误;
故选C.
【点睛】本题考查方位角的有关计算,正确理解方位角的有关概念及特殊角的余弦值是解题关键.
12.A
【分析】根据特殊锐角三角函数值以及锐角三角函数的增减性进行判断即可.
【详解】解:∵=,>,正弦值随着角度的增大而增大,
∴
∵α为锐角,
∴
故选:A.
【点睛】本题主要考查锐角三角函数,掌握特殊锐角三角函数值以及锐角三角函数的增减性是关键.
13.
【分析】过点D作DG⊥AF于点G,设,,运用,,,得出AD,DG的长,再通过翻折的性质及勾股定理,用n的代数式表示x,最后证明,通过相似三角形的性质得到答案.
【详解】解:如图,过点D作DG⊥AF于点G,设,,
∵△ABC为等边三角形,DG⊥AF,
∴,,
∵,
∴,.
∵,,
∴,,
∵△ABC为等边三角形,
∴,
∵,将△ABC沿DE折叠,使点B落在AC边上的点F处,
∴.
.
在中,
∵,
∴,
即,
化简得.
∵△ABC为等边三角形,
∴,
∵将△ABC沿DE折叠,使点B落在AC边上的点F处,
∴,
∴.
∵,
∴在中,有,
∵,
∴.
∵,
∴,
∴.
故答案为:.
【点睛】本题考查了解直角三角形,勾股定理以及相似三角形的判定及性质,综合性比较强,其中大胆设未知量是解题关键.
14.
【分析】根据正弦函数是对边比斜边,可得答案.
【详解】解:由题意作图如下:
由勾股定理可得AB===10,
∴,
故答案为:.
【点睛】本题考查了直角三角函数,利用正弦函数是对边比斜边是解题关键.
15./0.5
【分析】直接利用特殊角的三角函数值代入进而得出答案.
【详解】解:
= .
故答案为.
【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
16.
【分析】本题考查了计算器的基础知识,解题的关键是分析出按键中所求的问题.根据按键的显示,求的是余弦是的角的度数,按余弦的值写出度数即可.
【详解】解:∵余弦是的角的度数是,
故答案为:.
17.5
【分析】作CD⊥AB于D,据含30度的直角三角形三边的关系得到CD=,AD=3,再在Rt△BCD中根据正切的定义可计算出BD,然后把AD与BD相加即可.
【详解】解:作CD⊥AB于D,如图,
在Rt△ACD中,∠A=30°,AC=2,
∴CD=AC=,AD=CD=3,
在Rt△BCD中,tanB=,
∴,
∴BD=2,
∴AB=AD+BD=3+2=5.
【点睛】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
18.m=;△ABC是直角三角形.
【分析】先求出一元二次方程的解,再根据特殊角的三角函数值求出各角的度数,判断三角形的形状.
【详解】解:∵∠A=60°,
∴tanA=.
把x=代入方程2x2-3mx+3=0,得2()2-3m+3=0,解得m=.
把m=代入方程2x2-3mx+3=0得2x2-3mx+3=0,解得x1=,x2=.
∴cosB=,即∠B=30°.
∴∠C=180°-∠A-∠B=90°,
即△ABC是直角三角形.
【点睛】本题考查的知识点是解一元二次方程和判断三角形,解题关键是熟记特殊三角函数值.
19.1.4米.
【分析】过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,延长FC到点M,使得BE=CM,则EM=BC,在Rt△ABE、Rt△CDF中可求出AE、BE、DF、FC的长度,进而可得出EF的长度,再在Rt△MEF中利用勾股定理即可求出EM的长,此题得解.
【详解】过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,延长FC到点M,使得BE=CM,如图所示,
∵AB=CD,AB+CD=AD=2,
∴AB=CD=1,
在Rt△ABE中,AB=1,∠A=37°,
∴BE=AB sin∠A≈0.6,AE=AB cos∠A≈0.8,
在Rt△CDF中,CD=1,∠D=45°,
∴CF=CD sin∠D≈0.7,DF=CD cos∠D≈0.7,
∵BE⊥AD,CF⊥AD,
∴BE∥CM,
又∵BE=CM,
∴四边形BEMC为平行四边形,
∴BC=EM,CM=BE.
在Rt△MEF中,EF=AD﹣AE﹣DF=0.5,FM=CF+CM=1.3,
∴EM=≈1.4,
∴B与C之间的距离约为1.4米.
【点睛】本题考查了解直角三角形的应用、勾股定理以及平行四边形的判定与性质,正确添加辅助线,构造直角三角形,利用勾股定理求出BC的长度是解题的关键.
20.
【分析】本题考查了解直角三角形的应用即方向角问题,根据题目的已知条件,过点B作,垂足为D,根据题意可得:,,然后在中,利用锐角三角函数的定义求出和的长,再在中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系,进行计算即可解答.
【详解】解:过点B作,垂足为D,如下图:
由题意得: ,
,
在中,,
∴
在中:
;
∴
∴小宇家A到劳动基地C的距离约为:.
21.(1)
(2)
【分析】本题主要考查了特殊角三角函数值的混合计算,立方根和零指数幂:
(1)先计算特殊角三角函数值,立方根,再根据有理数四则混合计算法则求解即可;
(2)先计算特殊角三角函数值,零指数幂,再根据实数的运算法则求解即可.
【详解】(1)解:
;
(2)解:
.
22.(1)
(2)
【分析】(1)过点A作交于点E,由等腰三角形的性质得到,由勾股定理得到,由锐角三角函数的定义即可得到答案;
(2)过点A作交于点E,由,进一步即可得到的长.
【详解】(1)解:如图,过点A作交于点E,
∵,
∴,
∵,
∴,
在中,
∵,
∴,
∵,
∴,
∴..
在中,
∵,
∴.
(2)解:如图,同(1),过点A作交于点E,
∵,
∴,
又∵,
∴,
∴,
∵,
又∵由(1)求得,
∴.
【点睛】此题考查了等腰三角形的性质、勾股定理、锐角三角函数的定义等知识,熟练掌握等腰三角形的性质和勾股定理是解题的关键.
23.(1)∠A=30°,c=16,b=8;(2)∠B=45°,a=,c=2.
【详解】分析:
这是一组在直角三角形中,由已知边、角求未知边、角的题目,由已知条件根据直角三角形中边角间的关系进行分析解答即可.
详解:
(1)∵在Rt△ABC中,∠C=90°,a=8,∠B=60°,
∴∠A=90°-60°=30°,,;
(2)∵在Rt△ABC中,∠C=90°,∠A=45°,b=,
∴∠B=45°,,
∴.
点睛:这是一组在直角三角形中,由已知边、角求未知边、角的题目,熟悉“直角三角形中边、角间的关系”是正确解答这类题的关键.
24.
【分析】由是等腰三角形,求解 再利用锐角的正切的定义求解即可.
【详解】解: 是等腰三角形,
而
【点睛】本题考查的是等腰三角形的性质,锐角的正切的定义,掌握锐角的正切的定义是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章直角三角形的边角关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为( )
A. B. C. D.
2.如图,在菱形中,,,,则tan∠的值是( )
A. B.2 C. D.
3.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为( )
A.100米 B.110米 C.120米 D.130米
4.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1:,坝外斜坡的坡度i=1:1,则两个坡角的和为( )
A.90° B.60° C.75° D.105°
5.如图,王亮为了测量一条河流的宽度,他在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽(的长)可以表示为( )
A.米 B.米
C.米 D.米
6.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A.b=atanB B.a=ccosB C.c= D.a=bcosA
7.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
8.如图,在高为h的山顶上,测得一建筑物顶端与底部的俯角分别为30°和60°,用h表示这个建筑物的高度为( )
A.h B.h C.h D.h
9.如图,已知的边,直线的方程为,则( )
A. B. C. D.
10.如图,是斜边边上的高,,则( )
A. B. C. D.
11.如图,嘉淇一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法:①地在地的北偏西方向;②地在地的南偏西方向上;③;④.
其中错误的是( )
A.①② B.①③ C.②④ D.③④
12.已知>,那么锐角a的取值范围是( )
A. B. C. D.
二、填空题
13.如图,△ABC为等边三角形,点D,E分别在AB,BC上,将△ABC沿DE折叠,使点B落在AC边上的点F处,连接DF,EF,若,则 .(结果用含n的代数式表示)
14.在中,,则的值为
15.计算:cos245°+tan30°·sin60°-sin245°= .
16.用教材中的计算器按下列顺序依次按键:,屏幕上显示 .
17.如图,在△ABC中,∠A=30°,tanB=,AC=2,AB的长 .
三、解答题
18.在△ABC中,已知∠A=60°,∠B为锐角,且tanA,cosB恰为一元二次方程2x2-3mx+3=0的两个实数根.求m的值并判断△ABC的形状.
19.图1是一商场的推拉门,已知门的宽度米,且两扇门的大小相同(即),将左边的门绕门轴向里面旋转,将右边的门绕门轴向外面旋转,其示意图如图2,求此时与之间的距离(结果保留一位小数).(参考数据:,,)
20.周末,小红和小宇相约一起去郊外劳动基地参加劳动.已知小红家B在小宇家A的北偏西方向上,.两人到达劳动基地C处后,发现小宇家A在劳动基地C的南偏西方向上,小红家B在劳动基地C的南偏西方向上.求小宇家A到劳动基地C的距离.(结果保留1位小数;参考数据:,,,)
21.计算:
(1);
(2).
22.如图,在中,,,于点D.
(1)求的值;
(2)求的长.
23.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a=8,∠B=60°;
(2)在Rt△ABC中,∠C=90°,∠A=45°,b=.
24.如图,是等腰三角形,你能根据图中所给数据求出吗?
《第一章直角三角形的边角关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D C A D A A A B
题号 11 12
答案 C A
1.C
【分析】设与交于点E.由于阴影部分的面积,又,所以关键是求.为此,连接.根据易证,得出.在直角中,由正切的定义得出.再利用三角形的面积公式求出.
【详解】解:设与交于点E,连接.
在与中,,
,
∴(),
∴.
∵,
∴,
∴.
∴.
∴阴影部分的面积.
故选:C.
【点睛】本题主要考查了正方形、旋转的性质,直角三角形的判定及性质,图形的面积以及三角函数等知识,综合性较强,有一定难度.
2.B
【详解】解:设则
又因为在菱形ABCD中,
所以
,
由勾股定理知,
故答案为:B.
3.D
【分析】直接利用坡比的定义得出AC的长,再利用勾股定理得出AB的长.
【详解】解:∵某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,
∴=,
则=,
解得:AC=120米,
故AB===130(米).
故选:D.
【点睛】此题主要考查了解直角三角形的应用,正确掌握坡比的定义是解题关键.
4.C
【详解】解:如图所示,
∵ED:AE=1:,
∴∠A=30°.
∵CF:BF=1:1,
∴∠B=45°.
∴∠A+∠B=30°+45°=75°.
故选C.
【点睛】在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是这一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.
5.A
【分析】在中,利用的长,以及的度数,进而得到的度数,根据三角函数即可求得的长.
【详解】解:在中,
∵,,
∴,
∴,
∴,
即河宽米,
故选:A.
【点睛】此题考查了解直角三角形的应用-方向角问题,掌握方向角与正切函数的定义是解题的关键.
6.D
【详解】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
7.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
【点睛】本题主要考查了勾股定理,等腰直角三角形的性质,解直角三角形,熟练解直角三角形是解题的关键.
8.A
【分析】作CE⊥AB,根据∠DAB可以求得CE的长,根据CE即可求得AE的长,根据CD=BE=AB-AE即可解题.
【详解】解:作CE⊥AB,
∵∠DAB=90°-60°=30°,tan30°=
∴CE=BD=
∵∠ACE=30°,
∴AE=CEtan30°=
∴CD=BE=AB-AE==
故答案为.
【点睛】本题考查了特殊角的三角函数值,考查了直角三角形中三角函数的运用,本题中求得BD的长是解题的关键
9.A
【分析】本题考查了三角函数的定义和一次函数、勾股定理的知识,利用等角的代换,体现了思维的灵活性.根据一次函数的性质,求出点A、B的坐标,得到、的长度,再根据三角函数的定义即可求出的值.
【详解】直线的方程为
当时,;当时,,
∴,
∴
,
∵,
∴,
∵,
∴
∴
∴,
.
故选:A.
10.B
【分析】本题考查求锐角三角函数,勾股定理,
根据勾股定理先求出,再证明,进而即可求解
【详解】解:在中,
∵在和中,
,
故选B.
11.C
【分析】根据方位角及锐角三角函数的知识可以解得正确答案.
【详解】解:由题意可得如下标有角度的方位图,
∴B地在C地的北偏西 50°方向,①正确;A地在B地的南偏西 60°方向,②错误;
cos∠BAC=,③正确;∠ACB=90°-50°=40°,④错误;
故选C.
【点睛】本题考查方位角的有关计算,正确理解方位角的有关概念及特殊角的余弦值是解题关键.
12.A
【分析】根据特殊锐角三角函数值以及锐角三角函数的增减性进行判断即可.
【详解】解:∵=,>,正弦值随着角度的增大而增大,
∴
∵α为锐角,
∴
故选:A.
【点睛】本题主要考查锐角三角函数,掌握特殊锐角三角函数值以及锐角三角函数的增减性是关键.
13.
【分析】过点D作DG⊥AF于点G,设,,运用,,,得出AD,DG的长,再通过翻折的性质及勾股定理,用n的代数式表示x,最后证明,通过相似三角形的性质得到答案.
【详解】解:如图,过点D作DG⊥AF于点G,设,,
∵△ABC为等边三角形,DG⊥AF,
∴,,
∵,
∴,.
∵,,
∴,,
∵△ABC为等边三角形,
∴,
∵,将△ABC沿DE折叠,使点B落在AC边上的点F处,
∴.
.
在中,
∵,
∴,
即,
化简得.
∵△ABC为等边三角形,
∴,
∵将△ABC沿DE折叠,使点B落在AC边上的点F处,
∴,
∴.
∵,
∴在中,有,
∵,
∴.
∵,
∴,
∴.
故答案为:.
【点睛】本题考查了解直角三角形,勾股定理以及相似三角形的判定及性质,综合性比较强,其中大胆设未知量是解题关键.
14.
【分析】根据正弦函数是对边比斜边,可得答案.
【详解】解:由题意作图如下:
由勾股定理可得AB===10,
∴,
故答案为:.
【点睛】本题考查了直角三角函数,利用正弦函数是对边比斜边是解题关键.
15./0.5
【分析】直接利用特殊角的三角函数值代入进而得出答案.
【详解】解:
= .
故答案为.
【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
16.
【分析】本题考查了计算器的基础知识,解题的关键是分析出按键中所求的问题.根据按键的显示,求的是余弦是的角的度数,按余弦的值写出度数即可.
【详解】解:∵余弦是的角的度数是,
故答案为:.
17.5
【分析】作CD⊥AB于D,据含30度的直角三角形三边的关系得到CD=,AD=3,再在Rt△BCD中根据正切的定义可计算出BD,然后把AD与BD相加即可.
【详解】解:作CD⊥AB于D,如图,
在Rt△ACD中,∠A=30°,AC=2,
∴CD=AC=,AD=CD=3,
在Rt△BCD中,tanB=,
∴,
∴BD=2,
∴AB=AD+BD=3+2=5.
【点睛】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
18.m=;△ABC是直角三角形.
【分析】先求出一元二次方程的解,再根据特殊角的三角函数值求出各角的度数,判断三角形的形状.
【详解】解:∵∠A=60°,
∴tanA=.
把x=代入方程2x2-3mx+3=0,得2()2-3m+3=0,解得m=.
把m=代入方程2x2-3mx+3=0得2x2-3mx+3=0,解得x1=,x2=.
∴cosB=,即∠B=30°.
∴∠C=180°-∠A-∠B=90°,
即△ABC是直角三角形.
【点睛】本题考查的知识点是解一元二次方程和判断三角形,解题关键是熟记特殊三角函数值.
19.1.4米.
【分析】过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,延长FC到点M,使得BE=CM,则EM=BC,在Rt△ABE、Rt△CDF中可求出AE、BE、DF、FC的长度,进而可得出EF的长度,再在Rt△MEF中利用勾股定理即可求出EM的长,此题得解.
【详解】过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,延长FC到点M,使得BE=CM,如图所示,
∵AB=CD,AB+CD=AD=2,
∴AB=CD=1,
在Rt△ABE中,AB=1,∠A=37°,
∴BE=AB sin∠A≈0.6,AE=AB cos∠A≈0.8,
在Rt△CDF中,CD=1,∠D=45°,
∴CF=CD sin∠D≈0.7,DF=CD cos∠D≈0.7,
∵BE⊥AD,CF⊥AD,
∴BE∥CM,
又∵BE=CM,
∴四边形BEMC为平行四边形,
∴BC=EM,CM=BE.
在Rt△MEF中,EF=AD﹣AE﹣DF=0.5,FM=CF+CM=1.3,
∴EM=≈1.4,
∴B与C之间的距离约为1.4米.
【点睛】本题考查了解直角三角形的应用、勾股定理以及平行四边形的判定与性质,正确添加辅助线,构造直角三角形,利用勾股定理求出BC的长度是解题的关键.
20.
【分析】本题考查了解直角三角形的应用即方向角问题,根据题目的已知条件,过点B作,垂足为D,根据题意可得:,,然后在中,利用锐角三角函数的定义求出和的长,再在中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系,进行计算即可解答.
【详解】解:过点B作,垂足为D,如下图:
由题意得: ,
,
在中,,
∴
在中:
;
∴
∴小宇家A到劳动基地C的距离约为:.
21.(1)
(2)
【分析】本题主要考查了特殊角三角函数值的混合计算,立方根和零指数幂:
(1)先计算特殊角三角函数值,立方根,再根据有理数四则混合计算法则求解即可;
(2)先计算特殊角三角函数值,零指数幂,再根据实数的运算法则求解即可.
【详解】(1)解:
;
(2)解:
.
22.(1)
(2)
【分析】(1)过点A作交于点E,由等腰三角形的性质得到,由勾股定理得到,由锐角三角函数的定义即可得到答案;
(2)过点A作交于点E,由,进一步即可得到的长.
【详解】(1)解:如图,过点A作交于点E,
∵,
∴,
∵,
∴,
在中,
∵,
∴,
∵,
∴,
∴..
在中,
∵,
∴.
(2)解:如图,同(1),过点A作交于点E,
∵,
∴,
又∵,
∴,
∴,
∵,
又∵由(1)求得,
∴.
【点睛】此题考查了等腰三角形的性质、勾股定理、锐角三角函数的定义等知识,熟练掌握等腰三角形的性质和勾股定理是解题的关键.
23.(1)∠A=30°,c=16,b=8;(2)∠B=45°,a=,c=2.
【详解】分析:
这是一组在直角三角形中,由已知边、角求未知边、角的题目,由已知条件根据直角三角形中边角间的关系进行分析解答即可.
详解:
(1)∵在Rt△ABC中,∠C=90°,a=8,∠B=60°,
∴∠A=90°-60°=30°,,;
(2)∵在Rt△ABC中,∠C=90°,∠A=45°,b=,
∴∠B=45°,,
∴.
点睛:这是一组在直角三角形中,由已知边、角求未知边、角的题目,熟悉“直角三角形中边、角间的关系”是正确解答这类题的关键.
24.
【分析】由是等腰三角形,求解 再利用锐角的正切的定义求解即可.
【详解】解: 是等腰三角形,
而
【点睛】本题考查的是等腰三角形的性质,锐角的正切的定义,掌握锐角的正切的定义是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
