1.3三角函数的计算同步强化练习(含解析)
文档属性
| 名称 | 1.3三角函数的计算同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 704.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 18:56:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.3三角函数的计算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求,正确的按键顺序是( )
A.(2)(1)(4)(3) B.(1)(4)(2)(3)
C.(2)(4)(1)(3) D.(1)(2)(3)(4)
2.已知,运用科学计算器求锐角时(在开机状态下),按下的第一个键是( )
A. B.
C. D.
3.如图,△ABC中,∠ACB=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并用“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是( )
A.
B.
C.
D.
4.如果,那么锐角a的度数大约为( )
A. B. C. D.
5.在△ABC中,若=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
6.2cos60°的值等于( )
A.1 B. C. D.
7.一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. B. C.或 D.以上答案均不对
8.已知为锐角,且,则( )
A. B. C. D.
9.利用计算器求时,依次按键 则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
10.在中,若tanA=1,cosB=,则下列判断最确切的是( )
A.是等腰三角形 B.是等腰直角三角形
C.是直角三角形 D.是一般锐角三角形
11.利用科学计算器计算,下列按键顺序正确的是( )
A.
B.
C.
D.
12.在△ABC中,若,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
二、填空题
13.如图,在四边形中,连接,,,.若,,则 .
14.已知,则锐角 .
15.已知为锐角,且,则 .
16.用科学计算器计算:8cos31°+=
17.计算: .
三、解答题
18.计算:(1) ; (2).
19.利用计算器求下列各角(精确到1′).
(1)sinA=0.75,求∠A的度数;
(2)cosB=0.888 9,求∠B的度数;
(3)tanC=45.43,求∠C的度数;
(4)tanD=0.974 2,求∠D的度数.
20.利用计算器求下列各锐角的度数.(精确到)
(1),求;
(2),求;
(3),求;
(4),求.
21.用计算器求下列各式的值.(结果精确到)
(1);
(2);
(3).
22.计算:.
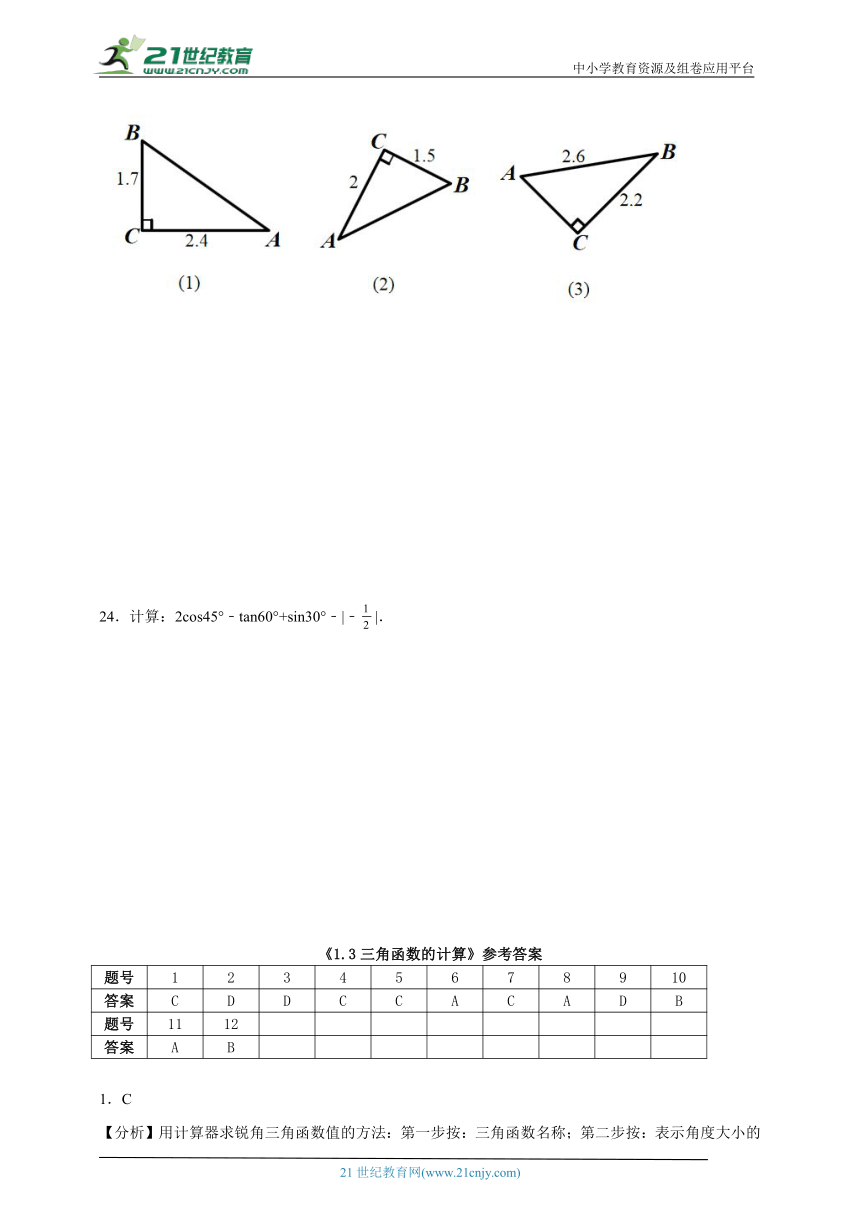
23.用计算器求图中的正弦值、余弦值和正切值.
24.计算:2cos45°﹣tan60°+sin30°﹣|﹣|.
《1.3三角函数的计算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C C A C A D B
题号 11 12
答案 A B
1.C
【分析】用计算器求锐角三角函数值的方法:第一步按:三角函数名称;第二步按:表示角度大小的数字;接下来第三步按:单位;第四步按:=;问题即可解答.
【详解】∵用计算器求的函数值的步骤为:
第一步按:sin,
第二步按:47,
第三步按:DMS,
第四步按:=,
∴正确的按键顺序是(2)(4)(1)(3),
故选C.
【点睛】本题属于计算器的应用,解此题需借助计算器的正确使用方法;
2.D
【分析】根据计算器求锐角的方法即可得结论.
【详解】∵cosA=0.2659,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,cos,0.2659,∴按下的第一个键是2ndF.
故选:D.
【点睛】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
3.D
【详解】∵tanA=,
故用计算器求锐角三角比的顺序为:
.
故选:D.
4.C
【详解】试题分析:使用2nd键,然后按tan-1 0.213即可求出∠α的度数.
∵tanα=0.213,
∴∠α≈12°.
故选C.
点睛:此题考查了使用计算器解决三角函数问题,解题关键是正确使用计算器.
5.C
【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.
【详解】解:由题意,得 cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=180°-60°-45°=75°.
故选C.
【点睛】此题主要考查了特殊角的三角函数值、非负数的性质,正确记忆特殊角的三角函数值是解题关键.
6.A
【详解】2cos60°=2×=1.
故选A.
7.C
【详解】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
8.A
【分析】利用特殊角的三角函数值求解即可.
【详解】解:∵,为锐角,
∴,
故选:A.
【点睛】本题考查根据三角函数值求角度,熟练掌握特殊角的三角函数值是解题的关键.
9.D
【分析】根据求解即可.
【详解】解:∵,
∴依次按键,则计算器上显示的值是1.
故选D.
【点睛】本题考查特殊角的三角函数值,熟悉计算器,熟知特殊角的三角函数值是解答的关键.
10.B
【分析】先根据正切值、余弦值求出、的度数,再根据三角形的内角和定理可得的度数,然后根据等腰直角三角形的定义即可得.
【详解】、是的内角,且,,
,,
,
是等腰直角三角形,
故选:B.
【点睛】本题考查了特殊角的正切值与余弦值、三角形的内角和定理、等腰直角三角形的定义,熟记特殊角的正切值与余弦值是解题关键.
11.A
【分析】简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【详解】
解:利用该型号计算器计算 ,按键顺序正确的是:
故选:A.
【点睛】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
12.B
【分析】根据得到∠B的度数,进一步求出∠C的度数,利用三角形内角和180°求出∠C度数即可判断
【详解】∵,
∴∠B与∠C均为锐角
∴∠B=60°,90°-∠C=30°
∴∠C=60°
∴∠A=180°-∠B-∠C=60°
∴该三角形为等边三角形
所以答案为B选项
【点睛】本题主要考查了特殊角的三角函数值,熟练掌握相关角度的三角函数值是解题关键
13.
【分析】过点C作BD垂线,垂足为E,设BE为x,DE为y,根据,可得为等腰直角三角形,以及可证,根据勾股定理和相似三角形的性质列方程求出x、y的值,即可求得BD的值.
【详解】解:如图:过点C作BD垂线,垂足为E,
在中,,
,
设BE为x,DE为y,
则根据勾股定理可得:,
即:,
,,
,
,
,
,即;
根据,
解得:,
则,
故答案为:.
【点睛】本题主要考查锐角三角函数,相似三角形,勾股定理等知识点,根据相似三角形性质以及勾股定理列出方程是解题的关键.
14.
【分析】利用计算器求正切值.
【详解】解:根据已知一个角的正切值求这个角的算法:先按,选择模式;再键入数字,最后按和;得到这三个角的度数.
答案为.
【点睛】本题要求同学们能熟练应用计算器,会用科学记算器进行三角函数计算.
15.
【分析】计算,并结合是个锐角,即可求解.
【详解】∵,
∴,
∴,
∵为锐角,
∴,
∴
故答案是:60°
【点睛】本题主要考查计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.
16.12.77
【详解】试题分析:8cos31°+=8×0.857+5.916=6.856+5.916=12.772≈12.77,
故答案为12.77.
点睛:熟练应用计算器,对计算器给出的结果,根据精确度的概念用四舍五入法取近似数.
17.
【分析】根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
【详解】,
故答案为.
【点睛】本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
18.(1)1;(2).
【分析】(1)先计算特殊角的正弦、余弦、余切值,再计算二次根式的乘除法与减法即可得;
(2)先计算特殊角的正弦与余弦值,再计算二次根式的除法与加减法即可得.
【详解】(1)原式,
,
;
(2)原式,
,
,
,
.
【点睛】本题考查了特殊角的三角函数值、二次根式的加减乘除运算,熟记各运算法则是解题关键.
19.(1)∠A≈48°35′(2)∠B≈27°16′(3)∠C≈88°44′(4)∠D≈44°15′
【分析】直接利用计算器计算即可.
【详解】解:(1)∵sinA=0.75,
∴∠A≈48.59°≈48°35′24″≈48°35′;
(2)∵cosB=0.888 9,
∴∠B≈27°16′12″≈27°16′;
(3)∵tanC=45.43,
∴∠C≈88°44′24″≈88°44′;
(4)∵tanD=0.974 2,
∴∠D≈44°15′6″≈44°15′.
【点睛】本题结合计算器的用法,旨在考查对基本概念的应用能力.
20.(1);(2);(3);(4)
【分析】直接利用计算器计算即可.
【详解】解:(1),∴;
(2)∵,∴;
(3)∵,∴;
(4)∵,∴.
【点睛】本题主要考查了用计算器求角度,旨在考查对基本概念的应用能力.
21.(1)
(2)
(3)
【分析】本题考查用计算器求三角函数的近似值,正确使用计算器是解题的关键.
(1)运用计算器即可计算出题中各式中的三角函数值.
(2)运用计算器即可计算出题中各式中的三角函数值.
(3)运用计算器即可计算出题中各式中的三角函数值.
【详解】(1);
(2);
(3).
22.
【分析】利用特殊角的三角函数值代入再通过实数运算法则求出即可.
【详解】原式=+
=(1﹣)×+
=﹣
=+.
【点睛】此题主要考查了特殊角的三角函数值应用,正确记忆特殊角的三角函数值是解题关键.
23.图(1),,;图(2),,;图(3),,
【分析】根据勾股定理求得另外一边的长度,在利用三角函数的定义求解即可.
【详解】解:由图(1)得,,
由勾股定理得:
,,
由图(2)得:,
由勾股定理得:
,,
由图(3)得:,
由勾股定理得:
,,
【点睛】此题考查了三角函数的定义,涉及了勾股定理,解题的关键是熟练掌握三角函数的有关定义.
24.
【分析】直接利用特殊角的三角函数值代入求出答案.
【详解】解:原式=2×﹣+﹣=﹣.
【点睛】本题考查特殊角的三角函数值.熟记特殊角的三角函数值是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3三角函数的计算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求,正确的按键顺序是( )
A.(2)(1)(4)(3) B.(1)(4)(2)(3)
C.(2)(4)(1)(3) D.(1)(2)(3)(4)
2.已知,运用科学计算器求锐角时(在开机状态下),按下的第一个键是( )
A. B.
C. D.
3.如图,△ABC中,∠ACB=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并用“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是( )
A.
B.
C.
D.
4.如果,那么锐角a的度数大约为( )
A. B. C. D.
5.在△ABC中,若=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
6.2cos60°的值等于( )
A.1 B. C. D.
7.一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. B. C.或 D.以上答案均不对
8.已知为锐角,且,则( )
A. B. C. D.
9.利用计算器求时,依次按键 则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
10.在中,若tanA=1,cosB=,则下列判断最确切的是( )
A.是等腰三角形 B.是等腰直角三角形
C.是直角三角形 D.是一般锐角三角形
11.利用科学计算器计算,下列按键顺序正确的是( )
A.
B.
C.
D.
12.在△ABC中,若,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
二、填空题
13.如图,在四边形中,连接,,,.若,,则 .
14.已知,则锐角 .
15.已知为锐角,且,则 .
16.用科学计算器计算:8cos31°+=
17.计算: .
三、解答题
18.计算:(1) ; (2).
19.利用计算器求下列各角(精确到1′).
(1)sinA=0.75,求∠A的度数;
(2)cosB=0.888 9,求∠B的度数;
(3)tanC=45.43,求∠C的度数;
(4)tanD=0.974 2,求∠D的度数.
20.利用计算器求下列各锐角的度数.(精确到)
(1),求;
(2),求;
(3),求;
(4),求.
21.用计算器求下列各式的值.(结果精确到)
(1);
(2);
(3).
22.计算:.
23.用计算器求图中的正弦值、余弦值和正切值.
24.计算:2cos45°﹣tan60°+sin30°﹣|﹣|.
《1.3三角函数的计算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C C A C A D B
题号 11 12
答案 A B
1.C
【分析】用计算器求锐角三角函数值的方法:第一步按:三角函数名称;第二步按:表示角度大小的数字;接下来第三步按:单位;第四步按:=;问题即可解答.
【详解】∵用计算器求的函数值的步骤为:
第一步按:sin,
第二步按:47,
第三步按:DMS,
第四步按:=,
∴正确的按键顺序是(2)(4)(1)(3),
故选C.
【点睛】本题属于计算器的应用,解此题需借助计算器的正确使用方法;
2.D
【分析】根据计算器求锐角的方法即可得结论.
【详解】∵cosA=0.2659,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,cos,0.2659,∴按下的第一个键是2ndF.
故选:D.
【点睛】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
3.D
【详解】∵tanA=,
故用计算器求锐角三角比的顺序为:
.
故选:D.
4.C
【详解】试题分析:使用2nd键,然后按tan-1 0.213即可求出∠α的度数.
∵tanα=0.213,
∴∠α≈12°.
故选C.
点睛:此题考查了使用计算器解决三角函数问题,解题关键是正确使用计算器.
5.C
【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.
【详解】解:由题意,得 cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=180°-60°-45°=75°.
故选C.
【点睛】此题主要考查了特殊角的三角函数值、非负数的性质,正确记忆特殊角的三角函数值是解题关键.
6.A
【详解】2cos60°=2×=1.
故选A.
7.C
【详解】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
8.A
【分析】利用特殊角的三角函数值求解即可.
【详解】解:∵,为锐角,
∴,
故选:A.
【点睛】本题考查根据三角函数值求角度,熟练掌握特殊角的三角函数值是解题的关键.
9.D
【分析】根据求解即可.
【详解】解:∵,
∴依次按键,则计算器上显示的值是1.
故选D.
【点睛】本题考查特殊角的三角函数值,熟悉计算器,熟知特殊角的三角函数值是解答的关键.
10.B
【分析】先根据正切值、余弦值求出、的度数,再根据三角形的内角和定理可得的度数,然后根据等腰直角三角形的定义即可得.
【详解】、是的内角,且,,
,,
,
是等腰直角三角形,
故选:B.
【点睛】本题考查了特殊角的正切值与余弦值、三角形的内角和定理、等腰直角三角形的定义,熟记特殊角的正切值与余弦值是解题关键.
11.A
【分析】简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【详解】
解:利用该型号计算器计算 ,按键顺序正确的是:
故选:A.
【点睛】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
12.B
【分析】根据得到∠B的度数,进一步求出∠C的度数,利用三角形内角和180°求出∠C度数即可判断
【详解】∵,
∴∠B与∠C均为锐角
∴∠B=60°,90°-∠C=30°
∴∠C=60°
∴∠A=180°-∠B-∠C=60°
∴该三角形为等边三角形
所以答案为B选项
【点睛】本题主要考查了特殊角的三角函数值,熟练掌握相关角度的三角函数值是解题关键
13.
【分析】过点C作BD垂线,垂足为E,设BE为x,DE为y,根据,可得为等腰直角三角形,以及可证,根据勾股定理和相似三角形的性质列方程求出x、y的值,即可求得BD的值.
【详解】解:如图:过点C作BD垂线,垂足为E,
在中,,
,
设BE为x,DE为y,
则根据勾股定理可得:,
即:,
,,
,
,
,
,即;
根据,
解得:,
则,
故答案为:.
【点睛】本题主要考查锐角三角函数,相似三角形,勾股定理等知识点,根据相似三角形性质以及勾股定理列出方程是解题的关键.
14.
【分析】利用计算器求正切值.
【详解】解:根据已知一个角的正切值求这个角的算法:先按,选择模式;再键入数字,最后按和;得到这三个角的度数.
答案为.
【点睛】本题要求同学们能熟练应用计算器,会用科学记算器进行三角函数计算.
15.
【分析】计算,并结合是个锐角,即可求解.
【详解】∵,
∴,
∴,
∵为锐角,
∴,
∴
故答案是:60°
【点睛】本题主要考查计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.
16.12.77
【详解】试题分析:8cos31°+=8×0.857+5.916=6.856+5.916=12.772≈12.77,
故答案为12.77.
点睛:熟练应用计算器,对计算器给出的结果,根据精确度的概念用四舍五入法取近似数.
17.
【分析】根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
【详解】,
故答案为.
【点睛】本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
18.(1)1;(2).
【分析】(1)先计算特殊角的正弦、余弦、余切值,再计算二次根式的乘除法与减法即可得;
(2)先计算特殊角的正弦与余弦值,再计算二次根式的除法与加减法即可得.
【详解】(1)原式,
,
;
(2)原式,
,
,
,
.
【点睛】本题考查了特殊角的三角函数值、二次根式的加减乘除运算,熟记各运算法则是解题关键.
19.(1)∠A≈48°35′(2)∠B≈27°16′(3)∠C≈88°44′(4)∠D≈44°15′
【分析】直接利用计算器计算即可.
【详解】解:(1)∵sinA=0.75,
∴∠A≈48.59°≈48°35′24″≈48°35′;
(2)∵cosB=0.888 9,
∴∠B≈27°16′12″≈27°16′;
(3)∵tanC=45.43,
∴∠C≈88°44′24″≈88°44′;
(4)∵tanD=0.974 2,
∴∠D≈44°15′6″≈44°15′.
【点睛】本题结合计算器的用法,旨在考查对基本概念的应用能力.
20.(1);(2);(3);(4)
【分析】直接利用计算器计算即可.
【详解】解:(1),∴;
(2)∵,∴;
(3)∵,∴;
(4)∵,∴.
【点睛】本题主要考查了用计算器求角度,旨在考查对基本概念的应用能力.
21.(1)
(2)
(3)
【分析】本题考查用计算器求三角函数的近似值,正确使用计算器是解题的关键.
(1)运用计算器即可计算出题中各式中的三角函数值.
(2)运用计算器即可计算出题中各式中的三角函数值.
(3)运用计算器即可计算出题中各式中的三角函数值.
【详解】(1);
(2);
(3).
22.
【分析】利用特殊角的三角函数值代入再通过实数运算法则求出即可.
【详解】原式=+
=(1﹣)×+
=﹣
=+.
【点睛】此题主要考查了特殊角的三角函数值应用,正确记忆特殊角的三角函数值是解题关键.
23.图(1),,;图(2),,;图(3),,
【分析】根据勾股定理求得另外一边的长度,在利用三角函数的定义求解即可.
【详解】解:由图(1)得,,
由勾股定理得:
,,
由图(2)得:,
由勾股定理得:
,,
由图(3)得:,
由勾股定理得:
,,
【点睛】此题考查了三角函数的定义,涉及了勾股定理,解题的关键是熟练掌握三角函数的有关定义.
24.
【分析】直接利用特殊角的三角函数值代入求出答案.
【详解】解:原式=2×﹣+﹣=﹣.
【点睛】本题考查特殊角的三角函数值.熟记特殊角的三角函数值是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
