1.5三角函数的应用同步强化练习(含解析)
文档属性
| 名称 | 1.5三角函数的应用同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 19:00:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.5三角函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度,钢管与地面所成角,那么钢管AB的长为( )
A. B. C. D.
2.从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30度,船离灯塔的水平距离为( )
A.米 B.米 C.21米 D.42米
3.如图,一艘轮船从位于灯塔的北偏东方向,距离灯塔北海里的小岛出发,沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,这时轮船与小岛的距离是( )
A.海里 B.海里 C.海里 D.海里
4.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时 刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.米 B.12米 C.米 D.10米
5.如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
A.60 B.30 C.15 D.45
6.“儿童放学归来早,忙趁东风放纸鸢”,小朋周末在公园草坪上放风筝,已知风筝拉线长80米且拉线与地面夹角为(如图所示,假设拉线是直的,小朋身高忽略不计),则风筝离地面的高度可以表示为( )
A. B. C. D.
7.某停车场入口栏杆如图,栏杆从水平位置AB绕点O旋转到CD的位置,已知AO=a,若栏杆的旋转角∠AOD=41°,则栏杆端点A上升的垂直距离为( )
A.asin41° B.acos41° C. D.atan41°
8.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
A.56米 B.66米 C.(56+20)米 D.(50+20)米
9.某超市从一楼到二楼有一自动扶梯,如图是自动扶梯的侧面示意图,已知自动扶梯AB的坡度为1:2.4,AB的长度为13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处侧得C点的仰角为 42°,则二楼的层高BC约为(精确到0.1米,,)( )
A.10.8米 B.8.9米 C.8.0米 D.5.8米
10.某人沿坡度i=1:的坡面向上走50米,则此人离地面的高度为( )
A.25米 B.50米 C.25米 D.50米
11.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
A.2海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里
12.在中,若,中线,,则的周长为( ).
A. B.
C. D.以上都不对
二、填空题
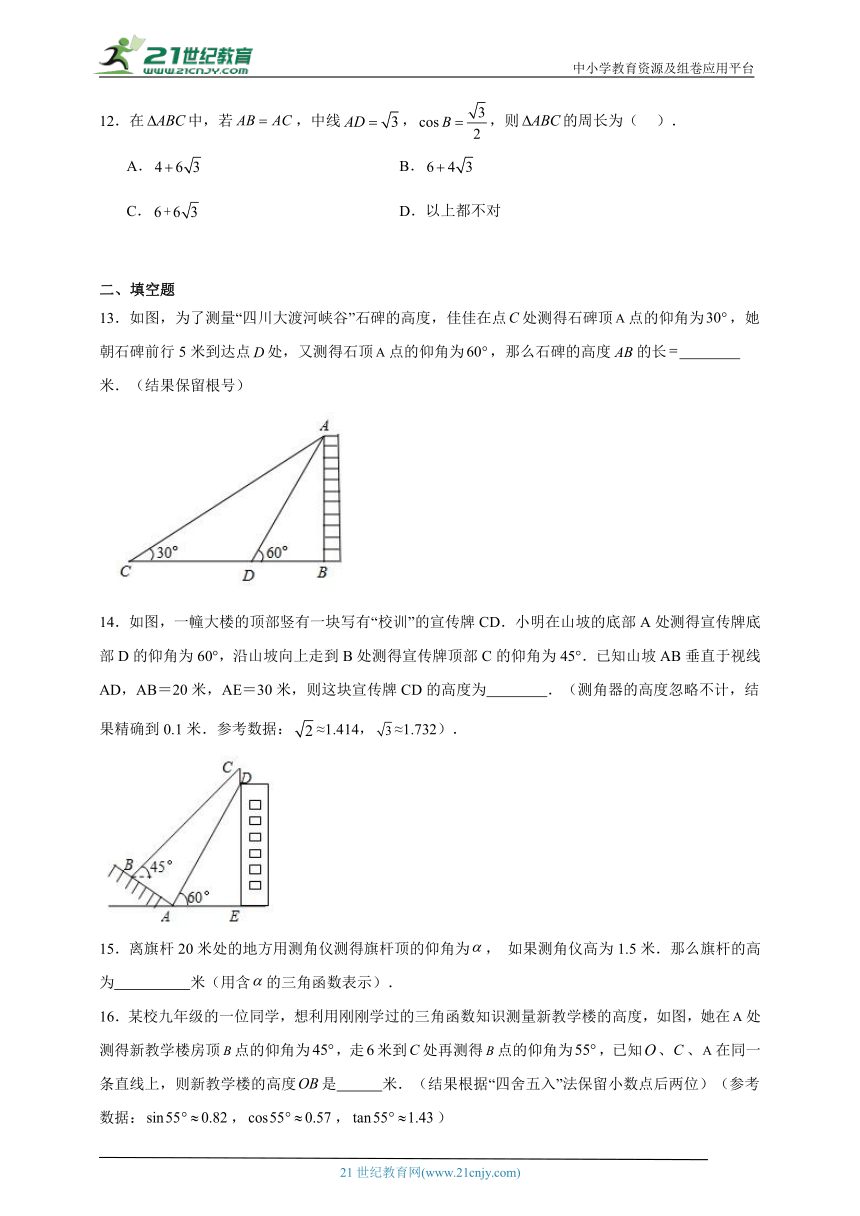
13.如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点处测得石碑顶点的仰角为,她朝石碑前行5米到达点处,又测得石顶点的仰角为,那么石碑的高度的长 米.(结果保留根号)
14.如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为 .(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732).
15.离旗杆20米处的地方用测角仪测得旗杆顶的仰角为, 如果测角仪高为1.5米.那么旗杆的高为 米(用含的三角函数表示).
16.某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在处测得新教学楼房顶点的仰角为,走米到处再测得点的仰角为,已知、、在同一条直线上,则新教学楼的高度是 米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:,,)
17.数学课外兴趣小组的同学们要测量被池塘隔开的两棵树A,B之间的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到点E处,再从点E沿着垂直于AE的方向走到点F处,C为AE上一点,其中三位同学分别测得三组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A,B两树之间的距离的有 组.
三、解答题
18.如图是引拉线固定电线杆的示意图,已知,,,求拉线的长.
19.某片绿地的形状如图所示,其中∠A=60°,AB⊥BC,AD⊥CD,AB=200m,CD=100m,求AD、BC的长.(精确到1m,≈1.732)
20.如图,两座建筑物的水平距离BC为,从A点测得D点的俯角为,测得C点的俯角为.求这两座建筑物的高度(结果保留小数点后一位).
21.如图,扶梯的坡比为:,滑梯的坡比为:,,.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,经过的总路程是多少米(要求先化简,再取近似值.结果精确到)?
22.如图,是一垂直于水平面的建筑物,一位同学从建筑物底端出发,沿水平方向向左行走11.6米到达点,再经过一段坡路,米,坡面的坡度(即),然后再沿水平方向向左行走4米到达点,在处测得建筑物顶端的仰角37°.
(1)求点到建筑物的水平距离;
(2)求建筑物的高度.(参考数据:,,,,,,,,均在同一平面内.)
23.求下列直角三角形中字母所表示的值.
24.如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.
《1.5三角函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D A B A A C D C
题号 11 12
答案 C B
1.A
【分析】根据锐角三角函数的正弦定义解题即可.
【详解】解:在中,,
,
故选:A.
【点睛】本题考查解直角三角形,涉及正弦,是重要考点,难度较易,掌握相关知识是解题关键.
2.A
【分析】在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
【详解】解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米).
故选:A.
【点睛】本题考查解直角三角形的应用-仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
3.D
【分析】过点C作CD⊥AB,则在Rt△ACD中易得AD和CD的长,再在直角△BCD中求出BD,相加可得AB的长.
【详解】解:过C作CD⊥AB于D点,
∴∠ACD=30°,∠BCD=45°,AC=60.
在Rt△ACD中,cos∠ACD,,
∴CD=AC cos∠ACD=60×=,,
在Rt△DCB中,∵∠BCD=∠B=45°,
∴CD=BD=30,
∴AB=AD+BD=30+30海里.
故选:D.
【点睛】此题主要考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
4.A
【分析】解直角三角形的应用(坡度坡角问题),锐角三角函数定义,特殊角的三角函数值,相似三角形的判定和性质.
【详解】延长AC交BF延长线于E点,则∠CFE=30°.
作CE⊥BD于E,在Rt△CFE中,∠CFE=30°,CF=4,
∴CE=2,EF=4cos30°=2,
在Rt△CED中,CE=2,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,
∴DE=4.
∴BD=BF+EF+ED=12+2.
∵△DCE∽△DAB,且CE:DE=1:2,
∴在Rt△ABD中,AB=BD=.
故选:A.
5.B
【分析】过点作,则点距离最近,解直角三角形求出即可.
【详解】:如图,过点作,则点距离最近,
由题意得:,
,
,
设速度为,则,
,
时间,
故行驶时间为时=分钟.
故选B
【点睛】本题考查了解直角三角形以及方向角的应用,从题目中提取数学模型是解题关键.
6.A
【分析】本题考查的是解直角三角形的应用—坡度坡角问题,如图,过点A作于C,根据正弦的定义解答即可.
【详解】解:如图,过点A作于C,
在中,,
则(米),
故选:A.
7.A
【分析】过点D作DF⊥AB于点F,根据锐角三角函数的定义即可求出答案.
【详解】解:过点D作DF⊥AB于点F,
则∠DFO=90°,
由题意可知:DO=AO=a,∠AOD=41°,
∵sin∠AOD=,
∴DF=asin41°.
故选:A.
【点睛】本题考查了解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义.
8.C
【分析】根据题意可得:BE=CF=20米,根据斜坡AB的坡比为1:2.5可得:AE=50米;根据∠D=30°,CF=20可得:DF=米,则AD=AE+EF+DF=(56+)米,即可求解.
【详解】解:如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
根据题意得:BE=CF=20米,EF=BC=6米,∠D=30°,
∵斜坡AB的坡度i=1:2.5,
∴,解得:AE=50米,
∵∠D=30°,
∴,
∴米,
∴米.
故选:C
【点睛】本题主要考查了解直角三角形,正确构造直角三角形是解题的关键.
9.D
【详解】试题分析:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD tan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
故选:D.
考点:解直角三角形的应用.
10.C
【分析】根据题意画出图形,由坡度可求出三角形的正切值,从而求出坡度角的度数,最后根据坡度角的度数求出AC即可.
【详解】如图,AB=50米,坡角为∠B=α,已知tanα==.
∴α=30°.
∴高AC=sinB AB=25(米).
故选:C.
【点睛】本题主要考查了解直角三角形的实际应用(坡度角问题),熟练地掌握三角函数的定义,特殊角度的三角函数值是解体的关键.
11.C
【详解】试题分析:首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP cos∠A=2cos55°海里.
解:如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,AP=2海里,
∴AB=AP cos∠A=2cos55°海里.
故选C.
考点:解直角三角形的应用-方向角问题.
12.B
【分析】根据等腰三角形的性质得出AD⊥BC,进而得出∠B的度数,再利用锐角三角函数关系求出BD的长,进而得出BC的长,即可得出答案.
【详解】
∵AB=AC,中线,
∴AD⊥BC,
∵,
∴∠B=30°,
∴AB=2AD=,
∴BD=×cos30°=3,
∴BC=3×2=6,AB=AC=,
∴△ABC的周长为:6++=6+.
故选B.
【点睛】本题主要考查了解直角三角形和等腰三角形的性质,根据已知得出AB的长是解题关键.
13.
【分析】先根据已知条件得出△ADC是等腰三角形,再利用AB=sin60°×AD计算即可
【详解】解:由题意可知:∠A=30°,∠ADB=60°
∴∠CAD=30°
∴△ADC是等腰三角形,
∴DA=DC又DC=5米
故AD=5米
在Rt△ADB中,∠ADB=60°
∴AB=sin60°×AD=米
故答案为:
【点睛】本题考查等腰三角形的性质、解直角三角形,熟练记忆特殊角的锐角三角函数值是关键
14.5.4米.
【详解】过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,∵∠AFB=90°,∠BAF=180°﹣60°﹣90°=30°,
∴BF=AB=10,AF=BF=,
∴BG=AF+AE=+30.
在Rt△BGC中,∵∠BGC=90°,∠CBG=45°,
∴CG=BG=+30.
Rt△ADE中,∵∠AED=90°,∠DAE=60°,AE=30,
∴DE=AE=,
∴CD=CG+GE﹣DE=+30+10﹣≈5.4.
故答案为5.4米.
考点:解直角三角形的应用-仰角俯角问题.
15.1.5 +20tan
【分析】由题意得,在直角三角形中,知道了已知角的邻边求对边,用正切值计算即可.
【详解】根据题意可得:旗杆比仪器高20tanα,测角仪高为1.5米,
故旗杆的高为(1.5+20tanα)米.
故答案为1.5+20tanα
【点睛】考查解直角三角形的应用,属于仰角问题,要求学生能借助仰角构造直角三角形是解题的关键.
16.
【分析】根据等腰直角三角形的性质得到,根据正切的定义列出方程,解方程求出.
【详解】解:在中,,
则,
米,
米,
在中,,
,
,
解得:,
故答案为:.
【点睛】本题考查的是解直角三角形的应用,仰角俯角问题,掌握锐角三角函数的定义是解题的关键.
17.3
【详解】【分析】(1)可利用∠ACB的正切来求AB的长;(2)可利用∠ACB和∠ADB的正切求出AB;(3)设AC=x,AD=CD+x,AB=,AB=.
【详解】此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故答案为3
【点睛】本题考查解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到解直角三角形即可求出.
18.
【分析】由于CD⊥AB,因此△ADC和△BDC都是直角三角形,在Rt△ACD中,由正弦的定义易得,代入相关数值,借助特殊角的三角函数值计算即可得到答案.
【详解】∵CD⊥AB,∠CAD=60°,
∴在Rt△ACD中,
∴AC=6(m).
答:拉线AC的长是6m.
【点睛】本题考查解直角三角形的应用. 由题意可知,本题需要借助解直角三角形的应用进行分析,能找出图中的直角三角形,并会利用三角函数列出已知角,已知边,需要的求边的关系式是解决此题的关键.
19.AD的长约为227m,BC的长约为146m.
【分析】延长AD,交BC的延长线于点E,则在与 中,根据三角函数就可求得BE,CE,AE与DE的长,就可求得AD与BC的长.
【详解】如图,延长AD,交BC的延长线于点E,
在Rt△ABE中,由AB=200m,得
在Rt△CDE中,由CD=100m,
得CE=2CD=200m,
答:AD的长约为227m,BC的长约为146m;
20.AB为,CD为.
【分析】首先分析图形:根据题意构造直角三角形,根据锐角的正切函数,即可求解.
【详解】解:过点D作DE⊥AB,
则四边形BCDE为矩形,
在Rt△ADE中,∠ADE==,DE=BC=,
∴AE=DEtan∠ADE=32.6×tan≈23.0m;
在Rt△ABC中,∠ACB==,BC=,
∴AB=BCtan=32.6×tan≈30.8m;
则DC=AB AE=30.83 23.00=7.8
∴AB为,CD为.
即两座建筑物的高度分别为,.
【点睛】本题考查解直角三角形的应用,首先构造直角三角形,再借助角边关系、三角函数的定义解题,难度一般.
21.
【分析】根据坡比分别求出、的长度,然后根据勾股定理求出、的长度,由求出的长,进而得出结果;
【详解】解:在中,(),
∴()
∴()
在中,(),;
∴()
∴()
∴()
∴
()
答:这个男孩经过的总路程约为
【点睛】本题考查了解直角三角形的应用、勾股定理、二次根式的运算等知识点;熟练根据坡比的定义以及勾股定理解直角三角形是解题的关键.
22.(1)18米;
(2)约为14.5米.
【分析】(1)延长EC交直线AB于M,则EM⊥AB,过C作CN⊥BF于N,则四边形BMCN是矩形,首先根据CD的坡度求出CN和ND,进而可得EM的值;
(2)在Rt△AEM中,根据37°的正切可得AM,再根据AB=AM+BM可得答案.
【详解】(1)解:延长EC交直线AB于M,则EM⊥AB,过C作CN⊥BF于N,
如图所示:
则四边形BMCN是矩形,
在Rt△CDN中,∵tan∠CDF=,
∴设CN=5a,则ND=12a,
∴CD==13a=2.6,
解得a=0.2,
∴CN=1米,ND=2.4米,
∴EM=EC+ND+BN=4+2.4+11.6=18(米),
答:点E到建筑物AB的水平距离是18米;
(2)解:在Rt△AEM中,
∵AM=EM tan37°≈18×0.75=13.5(米),
∴AB=AM+BM=13.5+1≈14.5(米).
答:建筑物AB的高度约为14.5米.
【点睛】本题考查的是矩形的性质、解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
23.(1),;(2),
【分析】(1) 根据特殊角60三角函数关系便可求出a,b
(2) 根据边的关系,边可以找到正切值,从而找到
【详解】(1)cos60
a=
tan60
b=4
(2)tan=
【点睛】抓特殊角的三角函数关系,这样便可以顺利找到答案了.
24.(1)30°;(2).
【详解】解:(1)连接BD,
∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°.
∵D是AC中点,∴BD是AC的垂直平分线.
∴AB=BC.∴∠A=∠C.
∵∠ABC=120°,∴∠A=∠C=30°.即∠ACB=30°.
(2)过点A作AE⊥BC于点E,
∵BC=3,∠ACB=30°,∠BDC=90°,
∴cos30°=.∴CD=.
∵AD=CD,∴AC=.
∵在Rt△AEC中,∠ACE=30°,∴.
∴点A到直线BC的距离为.
(1)根据垂直平分线的性质得出AB=BC,从而得出∠A=∠C=30°即可.
(2)根据BC=3,∠ACB=30°,∠BDC=90°,得出CD的长,从而求出AE的长度即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.5三角函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度,钢管与地面所成角,那么钢管AB的长为( )
A. B. C. D.
2.从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30度,船离灯塔的水平距离为( )
A.米 B.米 C.21米 D.42米
3.如图,一艘轮船从位于灯塔的北偏东方向,距离灯塔北海里的小岛出发,沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,这时轮船与小岛的距离是( )
A.海里 B.海里 C.海里 D.海里
4.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时 刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.米 B.12米 C.米 D.10米
5.如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
A.60 B.30 C.15 D.45
6.“儿童放学归来早,忙趁东风放纸鸢”,小朋周末在公园草坪上放风筝,已知风筝拉线长80米且拉线与地面夹角为(如图所示,假设拉线是直的,小朋身高忽略不计),则风筝离地面的高度可以表示为( )
A. B. C. D.
7.某停车场入口栏杆如图,栏杆从水平位置AB绕点O旋转到CD的位置,已知AO=a,若栏杆的旋转角∠AOD=41°,则栏杆端点A上升的垂直距离为( )
A.asin41° B.acos41° C. D.atan41°
8.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
A.56米 B.66米 C.(56+20)米 D.(50+20)米
9.某超市从一楼到二楼有一自动扶梯,如图是自动扶梯的侧面示意图,已知自动扶梯AB的坡度为1:2.4,AB的长度为13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处侧得C点的仰角为 42°,则二楼的层高BC约为(精确到0.1米,,)( )
A.10.8米 B.8.9米 C.8.0米 D.5.8米
10.某人沿坡度i=1:的坡面向上走50米,则此人离地面的高度为( )
A.25米 B.50米 C.25米 D.50米
11.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
A.2海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里
12.在中,若,中线,,则的周长为( ).
A. B.
C. D.以上都不对
二、填空题
13.如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点处测得石碑顶点的仰角为,她朝石碑前行5米到达点处,又测得石顶点的仰角为,那么石碑的高度的长 米.(结果保留根号)
14.如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为 .(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732).
15.离旗杆20米处的地方用测角仪测得旗杆顶的仰角为, 如果测角仪高为1.5米.那么旗杆的高为 米(用含的三角函数表示).
16.某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在处测得新教学楼房顶点的仰角为,走米到处再测得点的仰角为,已知、、在同一条直线上,则新教学楼的高度是 米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:,,)
17.数学课外兴趣小组的同学们要测量被池塘隔开的两棵树A,B之间的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到点E处,再从点E沿着垂直于AE的方向走到点F处,C为AE上一点,其中三位同学分别测得三组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A,B两树之间的距离的有 组.
三、解答题
18.如图是引拉线固定电线杆的示意图,已知,,,求拉线的长.
19.某片绿地的形状如图所示,其中∠A=60°,AB⊥BC,AD⊥CD,AB=200m,CD=100m,求AD、BC的长.(精确到1m,≈1.732)
20.如图,两座建筑物的水平距离BC为,从A点测得D点的俯角为,测得C点的俯角为.求这两座建筑物的高度(结果保留小数点后一位).
21.如图,扶梯的坡比为:,滑梯的坡比为:,,.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,经过的总路程是多少米(要求先化简,再取近似值.结果精确到)?
22.如图,是一垂直于水平面的建筑物,一位同学从建筑物底端出发,沿水平方向向左行走11.6米到达点,再经过一段坡路,米,坡面的坡度(即),然后再沿水平方向向左行走4米到达点,在处测得建筑物顶端的仰角37°.
(1)求点到建筑物的水平距离;
(2)求建筑物的高度.(参考数据:,,,,,,,,均在同一平面内.)
23.求下列直角三角形中字母所表示的值.
24.如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.
《1.5三角函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D A B A A C D C
题号 11 12
答案 C B
1.A
【分析】根据锐角三角函数的正弦定义解题即可.
【详解】解:在中,,
,
故选:A.
【点睛】本题考查解直角三角形,涉及正弦,是重要考点,难度较易,掌握相关知识是解题关键.
2.A
【分析】在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
【详解】解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米).
故选:A.
【点睛】本题考查解直角三角形的应用-仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
3.D
【分析】过点C作CD⊥AB,则在Rt△ACD中易得AD和CD的长,再在直角△BCD中求出BD,相加可得AB的长.
【详解】解:过C作CD⊥AB于D点,
∴∠ACD=30°,∠BCD=45°,AC=60.
在Rt△ACD中,cos∠ACD,,
∴CD=AC cos∠ACD=60×=,,
在Rt△DCB中,∵∠BCD=∠B=45°,
∴CD=BD=30,
∴AB=AD+BD=30+30海里.
故选:D.
【点睛】此题主要考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
4.A
【分析】解直角三角形的应用(坡度坡角问题),锐角三角函数定义,特殊角的三角函数值,相似三角形的判定和性质.
【详解】延长AC交BF延长线于E点,则∠CFE=30°.
作CE⊥BD于E,在Rt△CFE中,∠CFE=30°,CF=4,
∴CE=2,EF=4cos30°=2,
在Rt△CED中,CE=2,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,
∴DE=4.
∴BD=BF+EF+ED=12+2.
∵△DCE∽△DAB,且CE:DE=1:2,
∴在Rt△ABD中,AB=BD=.
故选:A.
5.B
【分析】过点作,则点距离最近,解直角三角形求出即可.
【详解】:如图,过点作,则点距离最近,
由题意得:,
,
,
设速度为,则,
,
时间,
故行驶时间为时=分钟.
故选B
【点睛】本题考查了解直角三角形以及方向角的应用,从题目中提取数学模型是解题关键.
6.A
【分析】本题考查的是解直角三角形的应用—坡度坡角问题,如图,过点A作于C,根据正弦的定义解答即可.
【详解】解:如图,过点A作于C,
在中,,
则(米),
故选:A.
7.A
【分析】过点D作DF⊥AB于点F,根据锐角三角函数的定义即可求出答案.
【详解】解:过点D作DF⊥AB于点F,
则∠DFO=90°,
由题意可知:DO=AO=a,∠AOD=41°,
∵sin∠AOD=,
∴DF=asin41°.
故选:A.
【点睛】本题考查了解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义.
8.C
【分析】根据题意可得:BE=CF=20米,根据斜坡AB的坡比为1:2.5可得:AE=50米;根据∠D=30°,CF=20可得:DF=米,则AD=AE+EF+DF=(56+)米,即可求解.
【详解】解:如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
根据题意得:BE=CF=20米,EF=BC=6米,∠D=30°,
∵斜坡AB的坡度i=1:2.5,
∴,解得:AE=50米,
∵∠D=30°,
∴,
∴米,
∴米.
故选:C
【点睛】本题主要考查了解直角三角形,正确构造直角三角形是解题的关键.
9.D
【详解】试题分析:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD tan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
故选:D.
考点:解直角三角形的应用.
10.C
【分析】根据题意画出图形,由坡度可求出三角形的正切值,从而求出坡度角的度数,最后根据坡度角的度数求出AC即可.
【详解】如图,AB=50米,坡角为∠B=α,已知tanα==.
∴α=30°.
∴高AC=sinB AB=25(米).
故选:C.
【点睛】本题主要考查了解直角三角形的实际应用(坡度角问题),熟练地掌握三角函数的定义,特殊角度的三角函数值是解体的关键.
11.C
【详解】试题分析:首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP cos∠A=2cos55°海里.
解:如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,AP=2海里,
∴AB=AP cos∠A=2cos55°海里.
故选C.
考点:解直角三角形的应用-方向角问题.
12.B
【分析】根据等腰三角形的性质得出AD⊥BC,进而得出∠B的度数,再利用锐角三角函数关系求出BD的长,进而得出BC的长,即可得出答案.
【详解】
∵AB=AC,中线,
∴AD⊥BC,
∵,
∴∠B=30°,
∴AB=2AD=,
∴BD=×cos30°=3,
∴BC=3×2=6,AB=AC=,
∴△ABC的周长为:6++=6+.
故选B.
【点睛】本题主要考查了解直角三角形和等腰三角形的性质,根据已知得出AB的长是解题关键.
13.
【分析】先根据已知条件得出△ADC是等腰三角形,再利用AB=sin60°×AD计算即可
【详解】解:由题意可知:∠A=30°,∠ADB=60°
∴∠CAD=30°
∴△ADC是等腰三角形,
∴DA=DC又DC=5米
故AD=5米
在Rt△ADB中,∠ADB=60°
∴AB=sin60°×AD=米
故答案为:
【点睛】本题考查等腰三角形的性质、解直角三角形,熟练记忆特殊角的锐角三角函数值是关键
14.5.4米.
【详解】过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,∵∠AFB=90°,∠BAF=180°﹣60°﹣90°=30°,
∴BF=AB=10,AF=BF=,
∴BG=AF+AE=+30.
在Rt△BGC中,∵∠BGC=90°,∠CBG=45°,
∴CG=BG=+30.
Rt△ADE中,∵∠AED=90°,∠DAE=60°,AE=30,
∴DE=AE=,
∴CD=CG+GE﹣DE=+30+10﹣≈5.4.
故答案为5.4米.
考点:解直角三角形的应用-仰角俯角问题.
15.1.5 +20tan
【分析】由题意得,在直角三角形中,知道了已知角的邻边求对边,用正切值计算即可.
【详解】根据题意可得:旗杆比仪器高20tanα,测角仪高为1.5米,
故旗杆的高为(1.5+20tanα)米.
故答案为1.5+20tanα
【点睛】考查解直角三角形的应用,属于仰角问题,要求学生能借助仰角构造直角三角形是解题的关键.
16.
【分析】根据等腰直角三角形的性质得到,根据正切的定义列出方程,解方程求出.
【详解】解:在中,,
则,
米,
米,
在中,,
,
,
解得:,
故答案为:.
【点睛】本题考查的是解直角三角形的应用,仰角俯角问题,掌握锐角三角函数的定义是解题的关键.
17.3
【详解】【分析】(1)可利用∠ACB的正切来求AB的长;(2)可利用∠ACB和∠ADB的正切求出AB;(3)设AC=x,AD=CD+x,AB=,AB=.
【详解】此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故答案为3
【点睛】本题考查解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到解直角三角形即可求出.
18.
【分析】由于CD⊥AB,因此△ADC和△BDC都是直角三角形,在Rt△ACD中,由正弦的定义易得,代入相关数值,借助特殊角的三角函数值计算即可得到答案.
【详解】∵CD⊥AB,∠CAD=60°,
∴在Rt△ACD中,
∴AC=6(m).
答:拉线AC的长是6m.
【点睛】本题考查解直角三角形的应用. 由题意可知,本题需要借助解直角三角形的应用进行分析,能找出图中的直角三角形,并会利用三角函数列出已知角,已知边,需要的求边的关系式是解决此题的关键.
19.AD的长约为227m,BC的长约为146m.
【分析】延长AD,交BC的延长线于点E,则在与 中,根据三角函数就可求得BE,CE,AE与DE的长,就可求得AD与BC的长.
【详解】如图,延长AD,交BC的延长线于点E,
在Rt△ABE中,由AB=200m,得
在Rt△CDE中,由CD=100m,
得CE=2CD=200m,
答:AD的长约为227m,BC的长约为146m;
20.AB为,CD为.
【分析】首先分析图形:根据题意构造直角三角形,根据锐角的正切函数,即可求解.
【详解】解:过点D作DE⊥AB,
则四边形BCDE为矩形,
在Rt△ADE中,∠ADE==,DE=BC=,
∴AE=DEtan∠ADE=32.6×tan≈23.0m;
在Rt△ABC中,∠ACB==,BC=,
∴AB=BCtan=32.6×tan≈30.8m;
则DC=AB AE=30.83 23.00=7.8
∴AB为,CD为.
即两座建筑物的高度分别为,.
【点睛】本题考查解直角三角形的应用,首先构造直角三角形,再借助角边关系、三角函数的定义解题,难度一般.
21.
【分析】根据坡比分别求出、的长度,然后根据勾股定理求出、的长度,由求出的长,进而得出结果;
【详解】解:在中,(),
∴()
∴()
在中,(),;
∴()
∴()
∴()
∴
()
答:这个男孩经过的总路程约为
【点睛】本题考查了解直角三角形的应用、勾股定理、二次根式的运算等知识点;熟练根据坡比的定义以及勾股定理解直角三角形是解题的关键.
22.(1)18米;
(2)约为14.5米.
【分析】(1)延长EC交直线AB于M,则EM⊥AB,过C作CN⊥BF于N,则四边形BMCN是矩形,首先根据CD的坡度求出CN和ND,进而可得EM的值;
(2)在Rt△AEM中,根据37°的正切可得AM,再根据AB=AM+BM可得答案.
【详解】(1)解:延长EC交直线AB于M,则EM⊥AB,过C作CN⊥BF于N,
如图所示:
则四边形BMCN是矩形,
在Rt△CDN中,∵tan∠CDF=,
∴设CN=5a,则ND=12a,
∴CD==13a=2.6,
解得a=0.2,
∴CN=1米,ND=2.4米,
∴EM=EC+ND+BN=4+2.4+11.6=18(米),
答:点E到建筑物AB的水平距离是18米;
(2)解:在Rt△AEM中,
∵AM=EM tan37°≈18×0.75=13.5(米),
∴AB=AM+BM=13.5+1≈14.5(米).
答:建筑物AB的高度约为14.5米.
【点睛】本题考查的是矩形的性质、解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
23.(1),;(2),
【分析】(1) 根据特殊角60三角函数关系便可求出a,b
(2) 根据边的关系,边可以找到正切值,从而找到
【详解】(1)cos60
a=
tan60
b=4
(2)tan=
【点睛】抓特殊角的三角函数关系,这样便可以顺利找到答案了.
24.(1)30°;(2).
【详解】解:(1)连接BD,
∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°.
∵D是AC中点,∴BD是AC的垂直平分线.
∴AB=BC.∴∠A=∠C.
∵∠ABC=120°,∴∠A=∠C=30°.即∠ACB=30°.
(2)过点A作AE⊥BC于点E,
∵BC=3,∠ACB=30°,∠BDC=90°,
∴cos30°=.∴CD=.
∵AD=CD,∴AC=.
∵在Rt△AEC中,∠ACE=30°,∴.
∴点A到直线BC的距离为.
(1)根据垂直平分线的性质得出AB=BC,从而得出∠A=∠C=30°即可.
(2)根据BC=3,∠ACB=30°,∠BDC=90°,得出CD的长,从而求出AE的长度即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
