1.6利用三角函数测高同步强化练习(含解析)
文档属性
| 名称 | 1.6利用三角函数测高同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 21:48:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
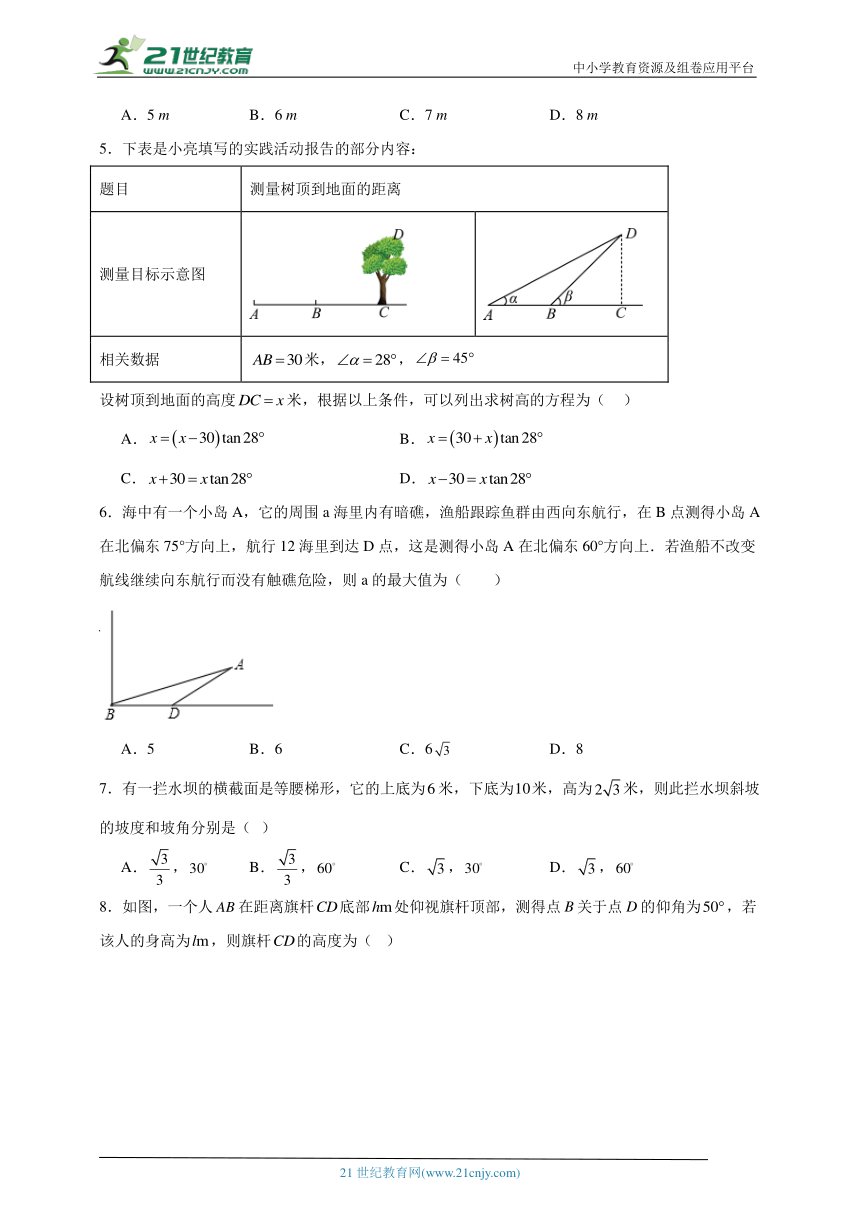
1.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.2km B.3km C.km D.3km
2.在测量过程中,常常会遇到仰角和俯角,图中是俯角的角是( )
A. B. C. D.
3.如图,点是航拍飞机在某一高度时的位置,是地平线,,,是某大型建筑物的斜面.从点观测点的偏角是( )
A. B. C. D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
5.下表是小亮填写的实践活动报告的部分内容:
题目 测量树顶到地面的距离
测量目标示意图
相关数据 米,,
设树顶到地面的高度米,根据以上条件,可以列出求树高的方程为( )
A. B.
C. D.
6.海中有一个小岛A,它的周围a海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东75°方向上,航行12海里到达D点,这是测得小岛A在北偏东60°方向上.若渔船不改变航线继续向东航行而没有触礁危险,则a的最大值为( )
A.5 B.6 C.6 D.8
7.有一拦水坝的横截面是等腰梯形,它的上底为米,下底为米,高为米,则此拦水坝斜坡的坡度和坡角分别是( )
A., B., C., D.,
8.如图,一个人在距离旗杆底部处仰视旗杆顶部,测得点B关于点D的仰角为,若该人的身高为,则旗杆的高度为( )
A. B. C. D.
9.如图,为一建筑物的最高点,在地面上的投影为,从地面上的点,用测角仪在处测得点的仰角为,测角仪高,若,则建筑物的高可表示为( )
A. B. C. D.
10.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )
A.(40+40)海里 B.(80)海里
C.(40+20)海里 D.80海里
11.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
12.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
A.
B.
C.
D.
二、填空题
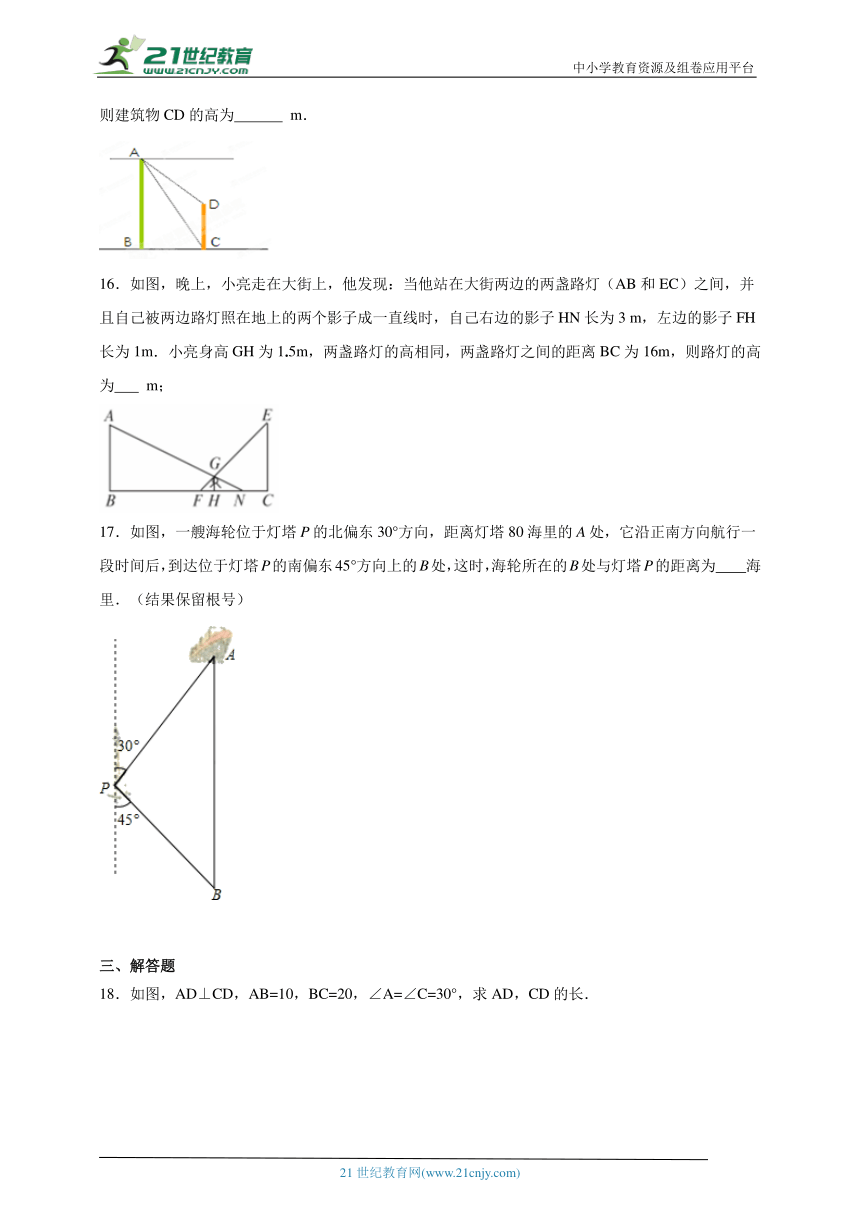
13.某市开展植树造林活动.如图,在坡度的山坡上植树,要求相邻两树间的水平距离为米,则斜坡上相邻两树间的坡面距离为 米.
14.2024年11月30日第一届河南省科技运动会在郑州举行,某参赛小组制作的“水火箭”成功发射,已知当“水火箭”上升到点时,位于地面的点到点的距离为米,仰角为,则此时“水火箭”距地面的高度可表示为 米.
15.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为 m.
16.如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和EC)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子HN长为3 m,左边的影子FH长为1m.小亮身高GH为1.5m,两盏路灯的高相同,两盏路灯之间的距离BC为16m,则路灯的高为 m;
17.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为 海里.(结果保留根号)
三、解答题
18.如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°,求AD,CD的长.
19.如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=37°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
20.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
21.为了测量某段河面的宽度,秋实同学设计了如图所示的测量方案;先在河的北岸选定一点A,再在河的南岸选定相距am的两点B,C,分别测得,.请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和α,β的三角函数表示)
22.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30 ,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45 ,请计算旗杆AB的高度(结果保留根号).
23.盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5 m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224 m到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.( 取1.73,结果精确到0.1 m)
24.如图是小明绘制的在家测量对面一幢楼房高度的示意图.图中点均在同一平面内,小明在家测量时的位置在点处,点到地面的距离m,想要测量高度的楼房是,小明在点处测得地面上一点的俯角是,楼房的最高点的仰角是,图中,,点在上,点到的距离m,请根据以上小明测得的数据,计算出楼房的高度.(结果精确到1m,参考数据:)
《1.6利用三角函数测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B B D C C A
题号 11 12
答案 C D
1.B
【详解】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B.
2.C
【分析】根据俯角的定义解答即可.本题考查了仰角,俯角,熟练掌握定义是解题的关键.
【详解】解:根据题意,是俯角的是.
故选:C.
3.B
【分析】本题考查了解直角三角形的应用的仰角俯角问题,熟练掌握俯角的定义是解题的关键.根据俯角的定义即可得到结论.
【详解】∵,是地平线,
∴从点观测点的俯角是,
故选:B.
4.C
【详解】过点C作AB的垂线CE,在Rt△AEC中,CE=BD=10, ∠CAE=30°,因为所以,AE=,
所以CD=BE=AB-AE=24-10故选C.
5.B
【分析】根据∠β=45°,得出BC=CD=x,再根据,用它的正切列方程即可.
【详解】解:∵,
∴BC=CD=x,
∵AB=30,
∴AC=x+30,
∴tan28°=,
∴x=(x+30)tan28°,
故选:B.
【点睛】本题考查解直角三角形,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.
6.B
【详解】试题分析:作AC⊥BD于点C, ∠ABD=90°-75°=15°,
∵∠ADC=90°-60°=30°, ∴∠BAD=∠ADC-∠ABD=30°-15°=15°,
∴∠ABD=∠BAD, ∴BD=AD=12(海里),
在直角△ADC中,AC=AD=×12=6(海里).故选B.
7.D
【分析】过A、D分别作AE⊥BC、DF⊥BC,那么ADEF平行四边形,所以BE=(BC-AD),而AE已知,所以坡度和坡角就可以解出.
【详解】解:如图,
过A、D分别作AE⊥BC、DF⊥BC.
∵ABCD为等腰梯形,
∴BE=(BC-AD)=2.
∴坡度==
∴坡角=∠B=60°
故选D.
【点睛】此题考查了学生对等腰梯形的性质,坡度坡角的计算等知识点的掌握情况.
8.C
【分析】本题主要考查了三角函数中正切函数的应用,通过构建直角三角形,利用正切函数求出相关线段的长度,进而得到旗杆的高度.解题的关键是理解仰角的概念,并能正确运用三角函数关系进行计算.
【详解】过点B,做,交与H,
在直角三角形中,,
根据正切函数的定义,,即,所以,
旗杆的高度等于人的身高加上的长度,即.
故选:C.
9.C
【分析】本题考查了解直角三角形的应用,过点D作于F,利用矩形的判定与性质得出,,利用锐角三角函数关系得出的长,即可得出的长.
【详解】解:过点D作于F,
由题意知:,,,
∴四边形是矩形,
∴,,
在中,,
∴.
故选:C.
10.A
【详解】试题分析:根据题意可得:△APC为等腰直角三角形,则AC=PC=40海里,根据Rt△BCP的性质可得:BC=40海里,则AB=AC+BC=(40+40)海里,故选A.
11.C
【详解】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C.
12.D
【详解】试题分析:利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
解:在Rt△AFG中,tan∠AFG=,
∴FG==,
在Rt△ACG中,tan∠ACG=,
∴CG==AG.
又∵CG﹣FG=30m,
即AG﹣=30m,
∴AG=15m,
∴AB=(15+2)m.
故选D.
考点:解直角三角形的应用-仰角俯角问题.
13.4
【分析】本题考查坡度问题,以及勾股定理,解题的关键在于熟练掌握相关知识。利用坡度求得垂直高度,进而利用勾股定理可求得相邻两树间的坡面距离.
【详解】解:坡比,,
,即,
解得,
(米),
故答案为:4.
14.
【分析】本题考查解直角三角形,熟记锐角三角函数的定义是解题关键,根据锐角的正弦函数的定义即可求解.
【详解】解:由题意得:
∴千米
故答案为:.
15.20m
【分析】延长CD交AM于点E.在Rt△ACE中,可求出CE;在Rt△ADE中,可求出DE.CD=CE-DE.
【详解】解:延长CD交AM于点E,则AE=30.
∴
同理可得
∴(米)
故答案为
【点睛】考查利用解直角三角形知识解决实际问题的能力.
16.7.5;
【详解】试题解析:设路灯的高为x米,
∵GH⊥BC,AB⊥BC,
∴GH∥AB.
∴△NGH∽△NAB.
∴①.
同理△FGH∽△FCE
②.
∴.
∴.
解得NB=15米,代入①得
,
解得x=7.5.
17.40
【分析】根据题意画出草图,再利用三角函数就可以求解出的距离.
【详解】解:作PC⊥AB于C,在Rt△PAC中,
∵PA=80,∠PAC=30°,
∴PC=40海里,
在Rt△PBC中,PC=40,∠PBC=∠BPC=45°,
∴PB=40海里,
故答案为40.
【点睛】本题主要考查三角函数的应用,通过构造直角三角形,利用三角函数来计算未知量,此类题目应当引起注意,是经常的考题模式.
18.AD=5+10,CD=10+5.
【详解】试题分析:此题可以过点B作两边的垂线,可得两个30°的直角三角形和一个矩形.根据30°的直角三角形的性质和矩形的性质就可求解.
解:如图所示,过B点分别作BE⊥AD于E,BF⊥CD于F.
由AD⊥CD知四边形BEDF为矩形.
则ED=BF,FD=BE.在Rt△AEB中,
∠AEB=90°,∠A=30°,AB=10.
∴BE=AB=5,AE=BE=5.
在Rt△CFB中,
∠CFB=90°,∠C=30°,BC=20,
∴BF=BC=10,CF=BF=10.
∴AD=AE+ED=5+10,
∴CD=CF+FD=10+5.
考点:解直角三角形.
19.(1) 36米;(2) 81米.
【详解】试题分析:(1)连接PA.在直角△PAH中利用勾股定理来求PH的长度;
(2)由题意知,隔音板的长度是PQ的长度.通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度,然后结合图形得到:PQ=PH+DQ﹣DH,把相关线段的长度代入求值即可.
试题解析:(1)如图,连接PA.
由题意知,AP=39m.
在直角△APH中,PH===36(米),
答:此时汽车与点H的距离为36米;
(2)由题意知,隔音板的长度是PQ的长度.
在Rt△ADH中,DH==20(米).
在Rt△CDQ中,DQ==65(米).
则PQ=PH+HQ=PH+DQ﹣DH=36+65﹣20=81(米).
答:高架道路旁安装的隔音板至少需要81米.
考点:解直角三角形的应用.
20.(1)1520m
(2)下山的速度是每分钟40米
【分析】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,分别解直角三角形即可.
(2)设下山的速度为x m/min,依据题意得,列分式方程求解即可.
【详解】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,
∴BF=200,CE=1000,
∵山坡AB的坡度为,
∴AF=480,
∴AB=520,
过B点作BG⊥CE于G点,
∴四边形BFEG是矩形,
∴EG=BF=200,
∴,
∵山坡BC的坡度为,
∴BG=600,
∴BC=1000,
∴山坡的长为(m) .
(2)∵∠D=30°,∠CED=90°,
∴CD=2000,
设下山的速度为x m/min,依据题意得,
,
解得,,
经检验,是原方程的根,
∴下山的速度是每分钟40米.
【点睛】本题考查了解直角三角形的坡比,坡角问题,熟练掌握化斜为直的解题方法是解题的关键.
21.河宽AD为m.
【分析】把△ABC分成两个有公共边的直角三角形,在这两个三角形中已知一边和一个锐角,满足解直角三角形的条件,可建立方程求得AD的长.
【详解】解:设.
在中,,
∴(m).
在中,,
∴(m).
∵,
∴,解得.
即河宽AD为:m.
【点睛】这两个直角三角形有公共的直角边,利用公共边的建立方程解决此类题目的基本出发点.
22.旗杆AB的高度是(8+8)米.
【分析】根据锐角三角函数可得(CD+DB)×=BD×1,解得BD,从而可以求得AB的高度.
【详解】,解:由题意可得,
CD=16米,
∵AB=CB tan30°,AB=BD tan45°,
∴CB tan30°=BD tan45°,
∴(CD+DB)×=BD×1,
解得BD=8+8,
∴AB=BD tan45°=(8+8)米,
即旗杆AB的高度是(8+8)米.
23.电视塔的高度AB约为195.3 m.
【详解】试题分析:本题主要考查三角函数,设AG=x,分别在Rt△ACG和Rt△Rt△AFG中
设AG=x,根据正切三角函数公式,用x表示出CG,FG的长度,根据DE=224m列出方程,解方程可求出x的值,从而求出AB的长.
在Rt△AFG中,∵tan∠AFG=,∴FG=,
在Rt△ACG中,∵tan∠ACG=,
∴CG==x,
∴x-=224,解得x≈193.8,
∴AB=193.8+1.5=195.3(m),
答:电视塔的高度AB约为195.3 m.
24.
【分析】本题主要考查矩形的判定和性质,含角的直角三角形,仰俯角解直角三角形的运用,掌握解直角三角形的计算是解题的关键.过点作于点,可得四边形是矩形,在中,,可得(负值舍去),,在中,运用仰俯角解直角三角形可得的值,由即可求解.
【详解】解:如图所示,过点作于点,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
∴在中,,
∴,,
∴,
解得,(负值舍去),
∴,
在中,,
∴,
∴,
∴楼房的高度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.2km B.3km C.km D.3km
2.在测量过程中,常常会遇到仰角和俯角,图中是俯角的角是( )
A. B. C. D.
3.如图,点是航拍飞机在某一高度时的位置,是地平线,,,是某大型建筑物的斜面.从点观测点的偏角是( )
A. B. C. D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
5.下表是小亮填写的实践活动报告的部分内容:
题目 测量树顶到地面的距离
测量目标示意图
相关数据 米,,
设树顶到地面的高度米,根据以上条件,可以列出求树高的方程为( )
A. B.
C. D.
6.海中有一个小岛A,它的周围a海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东75°方向上,航行12海里到达D点,这是测得小岛A在北偏东60°方向上.若渔船不改变航线继续向东航行而没有触礁危险,则a的最大值为( )
A.5 B.6 C.6 D.8
7.有一拦水坝的横截面是等腰梯形,它的上底为米,下底为米,高为米,则此拦水坝斜坡的坡度和坡角分别是( )
A., B., C., D.,
8.如图,一个人在距离旗杆底部处仰视旗杆顶部,测得点B关于点D的仰角为,若该人的身高为,则旗杆的高度为( )
A. B. C. D.
9.如图,为一建筑物的最高点,在地面上的投影为,从地面上的点,用测角仪在处测得点的仰角为,测角仪高,若,则建筑物的高可表示为( )
A. B. C. D.
10.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )
A.(40+40)海里 B.(80)海里
C.(40+20)海里 D.80海里
11.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
12.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
A.
B.
C.
D.
二、填空题
13.某市开展植树造林活动.如图,在坡度的山坡上植树,要求相邻两树间的水平距离为米,则斜坡上相邻两树间的坡面距离为 米.
14.2024年11月30日第一届河南省科技运动会在郑州举行,某参赛小组制作的“水火箭”成功发射,已知当“水火箭”上升到点时,位于地面的点到点的距离为米,仰角为,则此时“水火箭”距地面的高度可表示为 米.
15.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为 m.
16.如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和EC)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子HN长为3 m,左边的影子FH长为1m.小亮身高GH为1.5m,两盏路灯的高相同,两盏路灯之间的距离BC为16m,则路灯的高为 m;
17.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为 海里.(结果保留根号)
三、解答题
18.如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°,求AD,CD的长.
19.如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=37°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
20.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
21.为了测量某段河面的宽度,秋实同学设计了如图所示的测量方案;先在河的北岸选定一点A,再在河的南岸选定相距am的两点B,C,分别测得,.请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和α,β的三角函数表示)
22.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30 ,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45 ,请计算旗杆AB的高度(结果保留根号).
23.盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5 m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224 m到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.( 取1.73,结果精确到0.1 m)
24.如图是小明绘制的在家测量对面一幢楼房高度的示意图.图中点均在同一平面内,小明在家测量时的位置在点处,点到地面的距离m,想要测量高度的楼房是,小明在点处测得地面上一点的俯角是,楼房的最高点的仰角是,图中,,点在上,点到的距离m,请根据以上小明测得的数据,计算出楼房的高度.(结果精确到1m,参考数据:)
《1.6利用三角函数测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B B D C C A
题号 11 12
答案 C D
1.B
【详解】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B.
2.C
【分析】根据俯角的定义解答即可.本题考查了仰角,俯角,熟练掌握定义是解题的关键.
【详解】解:根据题意,是俯角的是.
故选:C.
3.B
【分析】本题考查了解直角三角形的应用的仰角俯角问题,熟练掌握俯角的定义是解题的关键.根据俯角的定义即可得到结论.
【详解】∵,是地平线,
∴从点观测点的俯角是,
故选:B.
4.C
【详解】过点C作AB的垂线CE,在Rt△AEC中,CE=BD=10, ∠CAE=30°,因为所以,AE=,
所以CD=BE=AB-AE=24-10故选C.
5.B
【分析】根据∠β=45°,得出BC=CD=x,再根据,用它的正切列方程即可.
【详解】解:∵,
∴BC=CD=x,
∵AB=30,
∴AC=x+30,
∴tan28°=,
∴x=(x+30)tan28°,
故选:B.
【点睛】本题考查解直角三角形,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.
6.B
【详解】试题分析:作AC⊥BD于点C, ∠ABD=90°-75°=15°,
∵∠ADC=90°-60°=30°, ∴∠BAD=∠ADC-∠ABD=30°-15°=15°,
∴∠ABD=∠BAD, ∴BD=AD=12(海里),
在直角△ADC中,AC=AD=×12=6(海里).故选B.
7.D
【分析】过A、D分别作AE⊥BC、DF⊥BC,那么ADEF平行四边形,所以BE=(BC-AD),而AE已知,所以坡度和坡角就可以解出.
【详解】解:如图,
过A、D分别作AE⊥BC、DF⊥BC.
∵ABCD为等腰梯形,
∴BE=(BC-AD)=2.
∴坡度==
∴坡角=∠B=60°
故选D.
【点睛】此题考查了学生对等腰梯形的性质,坡度坡角的计算等知识点的掌握情况.
8.C
【分析】本题主要考查了三角函数中正切函数的应用,通过构建直角三角形,利用正切函数求出相关线段的长度,进而得到旗杆的高度.解题的关键是理解仰角的概念,并能正确运用三角函数关系进行计算.
【详解】过点B,做,交与H,
在直角三角形中,,
根据正切函数的定义,,即,所以,
旗杆的高度等于人的身高加上的长度,即.
故选:C.
9.C
【分析】本题考查了解直角三角形的应用,过点D作于F,利用矩形的判定与性质得出,,利用锐角三角函数关系得出的长,即可得出的长.
【详解】解:过点D作于F,
由题意知:,,,
∴四边形是矩形,
∴,,
在中,,
∴.
故选:C.
10.A
【详解】试题分析:根据题意可得:△APC为等腰直角三角形,则AC=PC=40海里,根据Rt△BCP的性质可得:BC=40海里,则AB=AC+BC=(40+40)海里,故选A.
11.C
【详解】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C.
12.D
【详解】试题分析:利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
解:在Rt△AFG中,tan∠AFG=,
∴FG==,
在Rt△ACG中,tan∠ACG=,
∴CG==AG.
又∵CG﹣FG=30m,
即AG﹣=30m,
∴AG=15m,
∴AB=(15+2)m.
故选D.
考点:解直角三角形的应用-仰角俯角问题.
13.4
【分析】本题考查坡度问题,以及勾股定理,解题的关键在于熟练掌握相关知识。利用坡度求得垂直高度,进而利用勾股定理可求得相邻两树间的坡面距离.
【详解】解:坡比,,
,即,
解得,
(米),
故答案为:4.
14.
【分析】本题考查解直角三角形,熟记锐角三角函数的定义是解题关键,根据锐角的正弦函数的定义即可求解.
【详解】解:由题意得:
∴千米
故答案为:.
15.20m
【分析】延长CD交AM于点E.在Rt△ACE中,可求出CE;在Rt△ADE中,可求出DE.CD=CE-DE.
【详解】解:延长CD交AM于点E,则AE=30.
∴
同理可得
∴(米)
故答案为
【点睛】考查利用解直角三角形知识解决实际问题的能力.
16.7.5;
【详解】试题解析:设路灯的高为x米,
∵GH⊥BC,AB⊥BC,
∴GH∥AB.
∴△NGH∽△NAB.
∴①.
同理△FGH∽△FCE
②.
∴.
∴.
解得NB=15米,代入①得
,
解得x=7.5.
17.40
【分析】根据题意画出草图,再利用三角函数就可以求解出的距离.
【详解】解:作PC⊥AB于C,在Rt△PAC中,
∵PA=80,∠PAC=30°,
∴PC=40海里,
在Rt△PBC中,PC=40,∠PBC=∠BPC=45°,
∴PB=40海里,
故答案为40.
【点睛】本题主要考查三角函数的应用,通过构造直角三角形,利用三角函数来计算未知量,此类题目应当引起注意,是经常的考题模式.
18.AD=5+10,CD=10+5.
【详解】试题分析:此题可以过点B作两边的垂线,可得两个30°的直角三角形和一个矩形.根据30°的直角三角形的性质和矩形的性质就可求解.
解:如图所示,过B点分别作BE⊥AD于E,BF⊥CD于F.
由AD⊥CD知四边形BEDF为矩形.
则ED=BF,FD=BE.在Rt△AEB中,
∠AEB=90°,∠A=30°,AB=10.
∴BE=AB=5,AE=BE=5.
在Rt△CFB中,
∠CFB=90°,∠C=30°,BC=20,
∴BF=BC=10,CF=BF=10.
∴AD=AE+ED=5+10,
∴CD=CF+FD=10+5.
考点:解直角三角形.
19.(1) 36米;(2) 81米.
【详解】试题分析:(1)连接PA.在直角△PAH中利用勾股定理来求PH的长度;
(2)由题意知,隔音板的长度是PQ的长度.通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度,然后结合图形得到:PQ=PH+DQ﹣DH,把相关线段的长度代入求值即可.
试题解析:(1)如图,连接PA.
由题意知,AP=39m.
在直角△APH中,PH===36(米),
答:此时汽车与点H的距离为36米;
(2)由题意知,隔音板的长度是PQ的长度.
在Rt△ADH中,DH==20(米).
在Rt△CDQ中,DQ==65(米).
则PQ=PH+HQ=PH+DQ﹣DH=36+65﹣20=81(米).
答:高架道路旁安装的隔音板至少需要81米.
考点:解直角三角形的应用.
20.(1)1520m
(2)下山的速度是每分钟40米
【分析】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,分别解直角三角形即可.
(2)设下山的速度为x m/min,依据题意得,列分式方程求解即可.
【详解】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,
∴BF=200,CE=1000,
∵山坡AB的坡度为,
∴AF=480,
∴AB=520,
过B点作BG⊥CE于G点,
∴四边形BFEG是矩形,
∴EG=BF=200,
∴,
∵山坡BC的坡度为,
∴BG=600,
∴BC=1000,
∴山坡的长为(m) .
(2)∵∠D=30°,∠CED=90°,
∴CD=2000,
设下山的速度为x m/min,依据题意得,
,
解得,,
经检验,是原方程的根,
∴下山的速度是每分钟40米.
【点睛】本题考查了解直角三角形的坡比,坡角问题,熟练掌握化斜为直的解题方法是解题的关键.
21.河宽AD为m.
【分析】把△ABC分成两个有公共边的直角三角形,在这两个三角形中已知一边和一个锐角,满足解直角三角形的条件,可建立方程求得AD的长.
【详解】解:设.
在中,,
∴(m).
在中,,
∴(m).
∵,
∴,解得.
即河宽AD为:m.
【点睛】这两个直角三角形有公共的直角边,利用公共边的建立方程解决此类题目的基本出发点.
22.旗杆AB的高度是(8+8)米.
【分析】根据锐角三角函数可得(CD+DB)×=BD×1,解得BD,从而可以求得AB的高度.
【详解】,解:由题意可得,
CD=16米,
∵AB=CB tan30°,AB=BD tan45°,
∴CB tan30°=BD tan45°,
∴(CD+DB)×=BD×1,
解得BD=8+8,
∴AB=BD tan45°=(8+8)米,
即旗杆AB的高度是(8+8)米.
23.电视塔的高度AB约为195.3 m.
【详解】试题分析:本题主要考查三角函数,设AG=x,分别在Rt△ACG和Rt△Rt△AFG中
设AG=x,根据正切三角函数公式,用x表示出CG,FG的长度,根据DE=224m列出方程,解方程可求出x的值,从而求出AB的长.
在Rt△AFG中,∵tan∠AFG=,∴FG=,
在Rt△ACG中,∵tan∠ACG=,
∴CG==x,
∴x-=224,解得x≈193.8,
∴AB=193.8+1.5=195.3(m),
答:电视塔的高度AB约为195.3 m.
24.
【分析】本题主要考查矩形的判定和性质,含角的直角三角形,仰俯角解直角三角形的运用,掌握解直角三角形的计算是解题的关键.过点作于点,可得四边形是矩形,在中,,可得(负值舍去),,在中,运用仰俯角解直角三角形可得的值,由即可求解.
【详解】解:如图所示,过点作于点,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
∴在中,,
∴,,
∴,
解得,(负值舍去),
∴,
在中,,
∴,
∴,
∴楼房的高度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
