2.4二次函数的应用同步强化练习(含解析)
文档属性
| 名称 | 2.4二次函数的应用同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为,两侧距地面高处各有一盏灯,两灯间的水平距离为,则这个门洞内部顶端离地面的距离为( )
A. B.8 C. D.
2.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
3.在同一直角坐标系中与图象大致为
A. B. C. D.
4.如图,矩形OABC,点A的坐标为,AB=1.若抛物线与矩形OABC的边界总有两个公共点,则实数c的取值范围是( ).
A.c>8或c<-1 B.-1<c<8 C.c>1或c<-8 D.-8<c<1
5.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价,设平均每次降价的百分率为,降价后的价格为y元,原价为a元,则y与x的函数关系为( )
A. B. C. D.
6.如图所示,某大学的楼门是一抛物线形水泥建筑物,大门的地面宽度为,两侧距离地面高处各有一个挂校名横匾用的铁环,两铁环的水平距离为,则校门的高约为(精确到,水泥建筑物的厚度忽略不计)( )
A.9.2m B.9.1m C.9.0m D.8.9m
7.发射一枚炮弹,经过x秒后炮弹的高度为y米,x,y满足y=ax2+bx,其中a,b是常数,且a≠0.若此炮弹在第6秒与第14秒时的高度相等,则炮弹达到最大高度的时刻是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
8.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的图象大致是( ).
A. B. C. D.
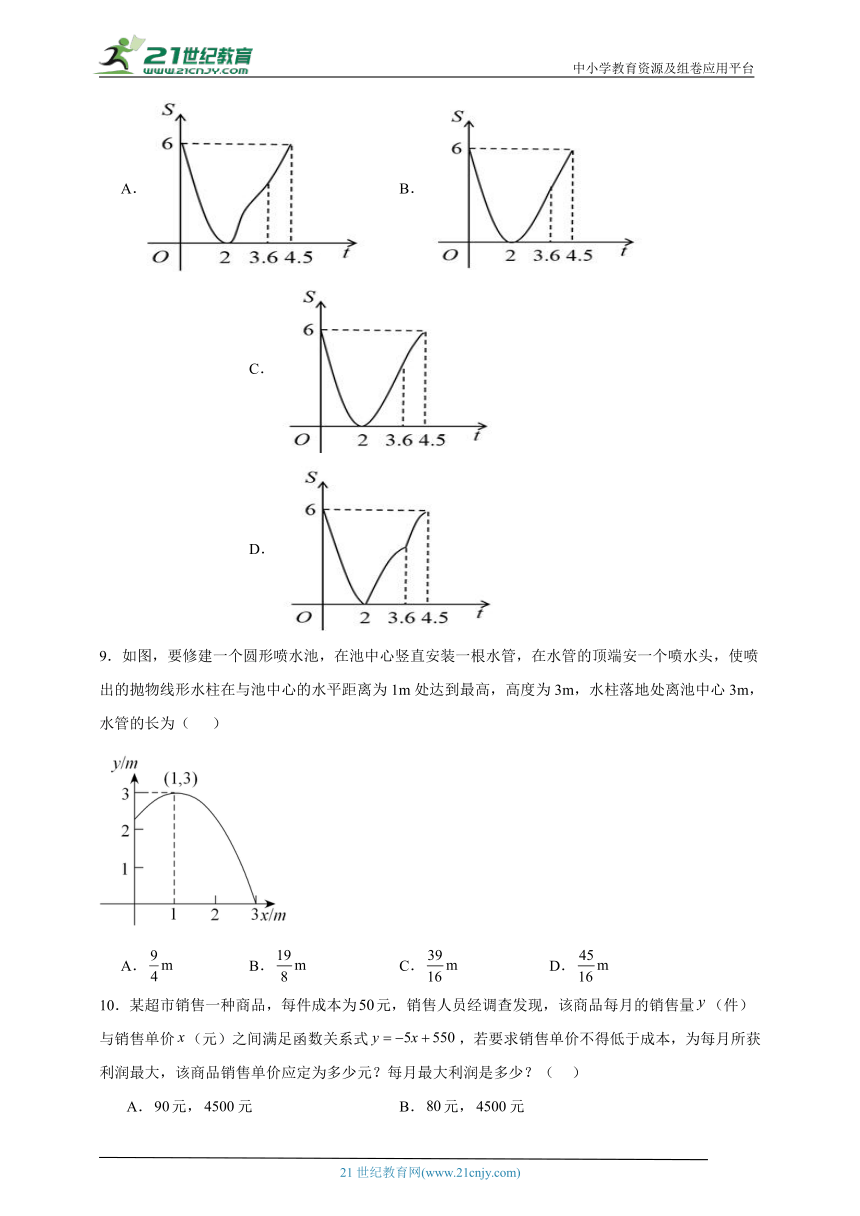
9.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
A. B. C. D.
10.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
11.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
12.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
二、填空题
13.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.若球能越过球网,又不出边界,则h的取值范围为 .
14.数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) 100 110 120 130 …
月销量(件) 200 180 160 140 …
已知该运动服的进价为每件60元,设售价为x(x≥100)元,则月销量是 件,销售该运动服的月利润为 元(用含x的式子表示).
15.如图,抛物线y=x2﹣2x﹣3交x轴于A(﹣1,0)、B(3,0),交y轴于C(0,﹣3),M是抛物线的顶点,现将抛物线沿平行于y轴的方向向上平移三个单位,则曲线CMB在平移过程中扫过的面积为 (面积单位).
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,则经过 s后,飞机停止滑行.
17.抛物线的顶点为,已知一次函数的图象经过点,则这个一次函数图象与两坐标轴所围成的三角形面积为 .
三、解答题
18.设抛物线经过A(-1,2),B(2,-1)两点,且与轴相交于点M.
(1)求和(用含的代数式表示);
(2)求抛物线上横坐标与纵坐标相等的点的坐标;
(3)在第(2)小题所求出的点中,有一个点也在抛物线上,试判断直线AM和轴的位置关系,并说明理由.
19.阅读材料:如图的三个顶点分别作出与水平线垂直的三条直线,外侧的两条平行线之间的距离叫做的“水平宽”,中间的这条直线在内部的线段的长度叫做的“铅垂高”,我们可以得到一种计算三角形面积的新方法:,即三角形的面积等于水平宽与铅垂高的乘积的一半.
解决下面的问题:
如图(2)已知抛物线过点三点,
(1)求抛物线的解析式.
(2)若为第三象限抛物线上的动点,其横坐标为,的面积为,求关于的解析式,并求的最大值.
20.如图,已知抛物线经过三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点P是直线l上的一个动点,当的周长最小时,求点P的坐标;
(3)点M也是直线l上的动点,且为等腰三角形,请直接写出所有符合条件的点M的坐标.
21.如图1,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A,B.与y轴交于点C.连接AC,BC.已知△ABC的面积为2.
(1)求抛物线的解析式;
(2)平行于x轴的直线与抛物线从左到右依次交于P,Q两点.过P,Q向x轴作垂线,垂足分别为G,H.若四边形PGHQ为正方形,求正方形的边长;
(3)如图2,平行于y轴的直线交抛物线于点M,交x轴于点N (2,0).点D是抛物线上A,M之间的一动点,且点D不与A,M重合,连接DB交MN于点E.连接AD并延长交MN于点F.在点D运动过程中,3NE+NF是否为定值?若是,求出这个定值;若不是,请说明理由.
22.如图,在平面直角坐标系中,平行四边形的边与y轴交于E点,F是的中点,B、C、D的坐标分别为.
(1)求过B、E、C三点的抛物线的解析式;
(2)试判断抛物线的顶点是否在直线上;
(3)设过F与平行的直线交y轴于Q,M是线段之间的动点,射线与抛物线交于另一点P,当的面积最大时,求P的坐标.
23.已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
24.已知某商品的销售量y(单位:件)与销售单价x(单位:元)之间有下了关系:当销售单价为20元时,卖出100件;当销售单价为15元时,卖出150个,该商品的进价为10元;
(1)求y与x的函数表达式,并指出自变量的取值范围;
(2)商家要尽快清空库存并要赚取最大利润,求此该商品的销售单价与此时的最大利润.
《2.4二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A D D B B B A B
题号 11 12
答案 D D
1.D
【分析】建立直角坐标系,得到二次函数,门洞高度即为二次函数的顶点的纵坐标.
【详解】解:如图,以地面为x轴,门洞中点为O点,画出y轴,建立直角坐标系,
由题意可知各点坐标为,,,
设抛物线解析式为把B、D两点带入解析式,
∴,解得:,
∴解析式为,则,
所以这个门洞内部顶端离地面的距离为,
故选D.
【点睛】本题考查二次函数的简单应用,能够建立直角坐标系解出二次函数解析式是本题关键.
2.C
【分析】根据已知得出直角坐标系,进而求出二次函数的解析式,再把代入抛物线的解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过顶点,则通过画图可得知为原点,
由平面直角坐标系可知,,即,
设抛物线的解析式为,
将点代入得:,解得,
则抛物线的解析式为,即,
当时,,
所以水面下降,
故选:C.
【点睛】本题主要考查了二次函数的应用,根据已知建立平面直角坐标系从而得出二次函数的解析式是解决问题的关键.
3.A
【分析】本题由一次函数图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
【详解】解:A、由抛物线可知,,,由直线可知,,,故本选项正确;
B、由抛物线可知,,,由直线可知,,,故本选项错误;
C、由抛物线可知,,,由直线可知,,,故本选项错误;
D、由抛物线可知,,,由直线可知,,,故本选项错误.
故选A.
【点睛】本题考查了一次函数和二次函数的图象解答该题时,一定要熟记一次函数、二次函数的图象的性质.
4.D
【分析】求得抛物线经过点A时的c的值,然后根据图象即可求得.
【详解】解:矩形OABC,点A的坐标为(2,0),AB=1,
∴OC=AB=1,
把A(2,0)代入y=2x2+c得,0=8+c,解得c= 8,
由图象可知, 8<c<1,故D正确.
故选:D.
【点睛】本题考查了二次函数图形与系数的关系,二次函数图象上点的坐标特征,矩形的性质,数形结合是解题的关键.
5.D
【详解】∴第一次降价后的价格是a×(1 x),
第二次降价为a×(1 x)×(1 x)=a(1 x)2
∴y=a(1 x)2.
故选D.
6.B
【分析】由题意可知,以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,抛物线过(0,0)、(8,0)、(1、4)、(7、4),运用待定系数法求出解析式后,求函数值的最大值即可.
【详解】解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,
则抛物线过O(0,0)、E(8,0)、A(1、4)、B(7、4)四点,
设该抛物线解析式为:y=ax2+bx+c,
则,
解得:.
.
故函数解析式为:y=-x2+x.
当x=4时,可得y=-≈9.1米,
故选B.
【点睛】本题考查点的坐标的求法及二次函数的实际应用关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标.
7.B
【详解】试题分析:由于炮弹在第6s与第14s时的高度相等,即x取6和14时y的值相等,根据抛物线的对称性可得到抛物线y=ax2+bx的对称轴为直线x="6+" =10,然后根据二次函数的最大值问题求解.
∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时间是10s.
故选B.
考点:二次函数的应用.
8.B
【分析】分别求出当时,时和时S关于t的函数解析式,再根据解析式判断函数图象即可.
【详解】解:由题意得:AB,
当时,点P在AC上,点Q在AB上,
则AP=AC-CP=4-2t,AQ=AB-BQ=5-2.5t,
如图,过点Q作QM⊥AC于M,
∴sin∠A=,即,
∴,
此时,
当时,点P在AB上,点Q在AC上,
则AP=2t-4,AQ=2.5t-5,
如图,过点P作PN⊥AC于N,
同理可得:,
此时,
∵二次函数的图象开口向上,对称轴为,
∴当时,函数图象为二次函数的图象的一部分,
当时,点Q与点C重合,点P在AB上,
此时,
∴当时,函数图象为直线的一部分,
故选:B.
【点睛】此题考查了动点问题的函数图象,正确表示出的面积并能够根据函数解析式选择相应的函数图象是解题的关键.
9.A
【分析】利用顶点式求得抛物线的解析式,再令x=0,求得相应的函数值,即为所求的答案.
【详解】解:由题意可知点(1,3)是抛物线的顶点,
∴设这段抛物线的解析式为y=a(x-1)2+3.
∵该抛物线过点(3,0),
∴0=a(3-1)2+3,
解得:a=-.
∴y=-(x-1)2+3.
∵当x=0时,y=-(0-1)2+3=-+3=,
∴水管应长m.
故选:A
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法及二次函数的相关性质是解题的关键.
10.B
【分析】设每月所获利润为w,按照等量关系列出二次函数,并根据二次函数的性质求得最值即可.
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
【点睛】本题考查了二次函数在实际生活中的应用,根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键.
11.D
【分析】将函数关系式转化为顶点式,然后利用开口方向和顶点坐标即可求出最多的利润.
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
【点睛】此题考查的是利用二次函数求最值,掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键.
12.D
【分析】设每件降价x元,由“每降低5元,每天可多售出10件”可知每降价1元可多售2件,根据题意可知每天的利润为(20+2x)(40-x),据此一一判断选项即可.
【详解】因为每降低5元,每天可多售出10件,所以每降价1元可多售2件,
设每件降价x元,每天的利润为y元,则每天可售(20+2x)件,每件利润为40-x,
所以每天的利润为
将整理成顶点式有,
由顶点式可知当销售单价降低15元时,每天获得利润最大,每天的最大利润为1250元,故A、B正确;
将x=10代入到解析式中解得y=1200,故C正确;
令y=1050,则,解得,即当每天的利润为1050元,则销售单价可能降低了5元,也可能降低了25元,所以D错误;
综上所述,答案选D.
【点睛】本题考查的是二次函数的实际应用,能够根据题意列出每天利润与降低单价的二次函数方程是解题的关键.
13.
【分析】把点A坐标代入y=a(x﹣6)2+h得y=(x﹣6)2+h,当x=9时,y>2.43,求出h取值范围,当x=18时,y≤0,求出h取值范围,综合即可求解.
【详解】解:点A(0,2),将点A的坐标代入抛物线表达式得:2=a(0﹣6)2+h,
解得:a=,
∴抛物线的表达式为y=(x﹣6)2+h,
由题意得:当x=9时,y=(x﹣6)2+h=(9﹣6)2+h>2.43,
解得:h>;
当x=18时,y=(x﹣6)2+h=(18﹣6)2+h≤0,
解得:h≥,
故h的取值范围是h≥.
故答案为:
【点睛】此题主要考查了二次函数的应用题,根据题意得到两个不等式并求出不等式组的解集是解题关键.
14.
【详解】分析:运用待定系数法求出月销量;根据月利润=每件的利润×月销量列出函数关系式.
详解:设月销量y与x的关系式为y=kx+b,
由题意得,,
解得.
则y=-2x+400;
由题意得,y=(x-60)(-2x+400)
=-2x2+520x-24000
点睛:本题考查的是二次函数的应用,一次函数的运用,掌握待定系数法求函数解析式是解题的关键.
15.9
【分析】由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积,求得四边形OCBD的面积即可.
【详解】解:如图所示,连接BC,OD,
由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积,
根据题意可得:OB=3,OC=3,BD=3,
所以,曲线CMB在平移过程中扫过的面积=OC×OB+ OB×BD=×3×3+×3×3=9.
故答案为:9.
【点睛】本题考查了二次函数图象与几何变换,由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积是解题的关键.
16.25
【分析】要求飞机从滑行到停止的路程,即求出函数取最大值时,t的值即可,因此将函数化为顶点式即可.
【详解】解:
所以当t=25时,该函数有最大值625
即第25秒时,飞机滑行最大距离625m停下来,
故答案为:25.
【点睛】本题主要考查了二次函数的应用,掌握二次函数求最值的方法,即公式法或配方法是解题关键.
17.1
【分析】易得顶点(2,-6),根据待定系数法,求出一次函数解析式,进而求出直线与坐标轴的交点,根据三角形的面积公式,即可求解.
【详解】∵抛物线,
∴顶点(2,-6),
∵一次函数的图象经过点,
∴,解得:k=,
∴一次函数解析式为:,
∴直线与坐标轴的交点坐标分别是:(0,3),(,0),
∴一次函数图象与两坐标轴所围成的三角形面积=.
故答案是:1.
【点睛】本题主要考查二次函数和一次函数图象与平面几何的综合,掌握一次函数图象与坐标轴的交点坐标的求法,是解题的关键.
18.(1);(2)(1,1),(-2,-2);(3)点(1,1)在抛物线时,直线AM∥轴;点(-2,-2)在抛物线时,直线AM与轴相交
【分析】(1)把A(-1,2),B(2,-1)两点分别代入抛物线y=ax2+bx+c,即可用a表示出b、c的值;(2)把(1)中所求b、c的值及x=y代入抛物线y=ax2-bx+c-1,即可求出符合条件的点的坐标;(3)把(2)中所求的两点分别代入(1)中抛物线的解析式,即可求出未知数的值,从而求出其解析式,根据其解析式可求出函数图象与y轴的交点坐标,根据其纵坐标与A点纵坐标的关系即可判断出直线AM与x轴的关系.
【详解】(1)∵抛物线y=ax2+bx+c经过A(-1,2),B(2,-1)两点,
∴,
解得.
(2)∵横坐标与纵坐标相等
∴由(1)得,抛物线y=ax2-bx+c-1的解析式是y=ax2+(a+1)x-2a=x,
即ax2+ax-2a=0,
∵a是抛物线解析式的二次项系数,
∴a≠0,
∴x2+x-2=0,
解得:x1=1,x2=-2,
∴抛物线y=ax2-bx+c-1满足条件的点的坐标是P1(1,1),P2(-2,-2).
(3)由(1)得抛物线y=ax2+bx+c的解析式是y=ax2-(a+1)x+1-2a,
①当P1(1,1)在抛物线上时,有a-(a+1)+1-2a=1,
解得a=-,
∴抛物线y=ax2+bx+c的解析式是y=-x2-x+2,它与y轴的交点是M(0,2)
∵点A(-1,2),M(0,2)两点的纵坐标相等,
∴直线AC平行于x轴.
②当P2(-2,-2)在抛物线上时,有4a+2(a+1)+1-2a=-2,
解得a=-,
∴抛物线的解析式为y=-x2+x+,它与y轴的交点是C(0,),
∵A、M两点的纵坐标不相等,
∴直线AM与x轴相交,
综上所述,当点(1,1)在抛物线y=ax2+bx+c上时,直线AM// x轴;当点(-2,-2)在抛物线y=ax2+bx+c上时,直线AM与x轴相交.
【点睛】本题考查了用代入法求函数解析式,抛物线上点的坐标特征.第(3)小题要将(2)中所求点代入解析式进行分类讨论.
19.(1);(2),4
【分析】(1)根据题意,可设出抛物线解析式,代入A、B、C点的坐标,即可得出抛物线的解析式;
(2)根据待定系数法得出直线AB的解析式为,由题意可得即可求解.
【详解】解:由题可设抛物线解析式为,
且已知抛物线过点,
将其带入可得
解得
则抛物线解析式为.
由点可得直线的解析式为,
由题意可得
.
则可得当时,
有最大值为.
【点睛】此题主要考查二次函数在给定区间上的最值、二次函数综合题、待定系数法求二次函数解析式,熟练掌握二次函数的图象和性质是解题关键.
20.(1);(2)(1,﹣2);(3)(1,﹣)或(1,)或(1,﹣1)或(1,0)
【分析】(1)根据点A、B、C的坐标,利用待定系数法求解抛物线的函数解析式即可;
(2)因为AC为定值,要使的周长最小,只需PA+PC最小即可,根据抛物线的对称性,连接BC交l于点P,此时PA+PC最小为BC的长,由点B、C坐标求出直线BC的函数解析式,利用二次函数的性质和一次函数图像上的点的坐标特征即可求得点P坐标;
(3)设点M(1,m),分AM=AC、AM=MC、AC=MC三种情况讨论求解即可.
【详解】解:(1)将点代入中,
得:,解得:,
∴抛物线的函数关系式为;
(2)因为AC为定值,要使的周长最小,只需PA+PC最小即可,
连接BC交l于点P,此时PA+PC取得最小值,如图,
设直线AB的函数解析式为y=kx+t(k≠0),
将代入,
得:,解得:,
∴直线BC的函数解析式为y=x﹣3,
∵,
∴抛物线的对称轴为直线x=1,即点P的横坐标为1,
将x=1代入y=x﹣3中,得:y=1﹣3=﹣2,
∴点P坐标为(1,﹣2);
(3)设点M(1,m),则,,
,
分三种情况讨论:
①当AM=AC时,有=10,
解得:,
∴点M的坐标为(1,﹣)或(1,);
②当AM=MC时,有=,
解得:m=﹣1,
∴点M的坐标为(1,﹣1);
③当AC=MC时,有10=,
解得:,
∴点M的坐标为(1,0)或(1,﹣6),
设直线AC的函数解析式为y=px+q,
将代入,
得:,解得:,
∴直线AC的函数解析式为y=﹣3x﹣3,
∵当x=1时,y=﹣3﹣3=﹣6,
∴点M(1,﹣6)在直线AC上,即点A、C、M不能组成三角形,
故满足题意的点M的坐标为(1,﹣)或(1,)或(1,﹣1)或(1,0).
【点睛】本题考查了待定系数法求二函数的解析式、求一次函数的解析式、轴对称中的最短路径问题、图像上点的坐标特征、两点间的距离公式以及等腰三角形的性质,解答的关键是认真审题,寻找相关联的信息,利用待定系数法、数形结合和分类讨论的思想方法进行推理、探究和计算.
21.(1);(2)或;(3)是,3NE+NF为定值4
【分析】(1)先将抛物线解析式变形,可得A和B的坐标,从而得AB=1+3=4,根据三角形ABC的面积为2可得OC的长,确定点C的坐标,根据点C的坐标,利用待定系数法即可求出二次函数的解析式;
(2)设点P的纵坐标为m,当y=m时,﹣x2+x+1=m,解方程可得P和Q两点的坐标,从而得G和H的坐标,再利用正方形的性质可得出关于m的方程,解之即可得出结论;
(3)设点D(n,﹣n2+n+1),利用待定系数法求直线AD和BD的解析式,表示FN和OK的长,直接代入计算可得结论.
【详解】(1)如图1,y=ax2﹣2ax﹣3a=a(x2﹣2x﹣3)=a(x﹣3)(x+1),
∴A(﹣1,0),B(3,0),
∴AB=4,
∵△ABC的面积为2,即,
∴OC=1,
∴C(0,1),
将C(0,1)代入y=ax2﹣2ax﹣3a,得:﹣3a=1,
∴a=﹣,
∴该二次函数的解析式为y=﹣x2+x+1;
(2)如图2,设点P的纵坐标为m,当y=m时,﹣x2+x+1=m,
解得:x1=1+,x2=1﹣,
∴点P的坐标为(1﹣,m),点Q的坐标为(1+,m),
∴点G的坐标为(1﹣,0),点H的坐标为(1+,0),
∵矩形PGHQ为正方形,
∴PQ=PG,
∴1+﹣(1﹣)=m,
解得:m1=﹣6﹣2,m2=﹣6+2,
∴当四边形PGHQ为正方形时,边长为6+2或2﹣6;
(3)如图3,设点D(n,﹣n2+n+1),延长BD交y轴于K,
∵A(﹣1,0),
设AD的解析式为:y=kx+b,
则,解得:,
∴AD的解析式为:y=(﹣)x﹣,
当x=2时,y=﹣n+2﹣n+1=﹣n+3,
∴F(2,3﹣n),
∴FN=3﹣n,
同理得直线BD的解析式为:y=(﹣)x+n+1,
∴K(0,n+1),
∴OK=n+1,
∵N(2,0),B(3,0),
∴,
∵EN∥OK,
∴,
∴OK=3EN,
∴3EN+FN=OK+FN=n+1+3﹣n=4,
∴在点D运动过程中,3NE+NF为定值4.
【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、正方形的性质、待定系数法求一次函数解析式以及平行线分线段成比例定理等知识,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用正方形的性质,找出关于m的方程;(3)利用AD和BD的解析式确定FN和OK的长,可解决问题.
22.(1);(2)顶点是在直线上,理由见解析;(3)P点坐标为(9,).
【分析】(1)先求出A点坐标,再求出直线AB的解析式,进而求得E的坐标,然后用待定系数法解答即可;
(2)先求出点F的坐标,再求出直线EF的解析式,然后根据抛物线的解析式确定顶点坐标,然后进行判定即可;
(3)设P点坐标为(p,),求出直线BP的解析式,进而求得M的坐标;再求FQ的解析式,确定Q的坐标,可得|MQ|=+6,最后根据S△PBQ= S△MBQ+ S△PMQ列出关于p的二次函数并根据二次函数的性质求最值即可.
【详解】解:(1)∵平行四边形,B、C、D的坐标分别为
∴A(3,10),
设直线AB的解析式为y=kx+b,
则 ,解得,
∴直线AB的解析式为y=2x+4,
当x=0时,y=4,则E的坐标为(0,4),
设抛物线的解析式为:y=ax2+bx+c,
,解得,
∴过B、E、C三点的抛物线的解析式为;
(2)顶点是在直线上,理由如下:
∵F是的中点,
∴F(8,10),
设直线EF的解析式为y=mx+n,
则,解得,
∴直线EF的解析式为y=x+4,
∵,
∴抛物线的顶点坐标为(3,),
∵=×3+4,
∴抛物线的顶点是否在直线上;
(3)∵,则设P点坐标为(p,),直线BP的解析式为y=dx+e,
则 ,解得,
∴直线EF的解析式为y=,
当x=0时,y=,则M点坐标为(0,),
∵AB//FQ ,
∴设FQ的解析式为y=2x+f,则10=2×8+f,解得f=-6,
∴FQ的解析式为y=2x-6 ,
∴Q的坐标为(0,-6),
∴|MQ|=+6,
∴S△PBQ= S△MBQ+ S△PMQ
=
=
=
=
∴当p=9时,的面积最大时,
∴P点坐标为(9,).
【点睛】本题主要考查了运用待定系数法求函数解析式、二次函数求最值等知识点,灵活求得所需的函数解析式成为解答本题的关键.
23.(Ⅰ)a=﹣;(Ⅱ)(i)y=﹣ x2+1;(ii)证明见解析.
【分析】(1)可用a表示出抛物线的顶点坐标,再代入直线方程可求得a的值,
(2)(i)由于k为任意非零实数,可取k=1和k=2,再联立两解析式消去y,得到的一元二次方程有两个相等的实数根可得到两个关于a、b的方程,可求得a、b的值,即可求得拋物线解析式; (ii)设出P点坐标,连接OP,过P作PQ⊥直线y=2,作PD⊥x轴于点D,可分别表示出OP和PQ,可证明其相等
【详解】解:(1)将k=1,b=1代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x.
∵y=ax2+x+1=a(x+ )2+1﹣ ,
∴抛物线的顶点为(﹣ ,1﹣ ).
∵抛物线的顶点在直线y=x上,
∴﹣ =1﹣ ,
解得:a=﹣ .
(2)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1.
∵无论非零实数k取何值,直线与抛物线都只有一个交点,
∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根,
∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0.
∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立,
∴4a+1=0且b=0,
∴a=﹣ ,b=0.
∴抛物线的解析式为y=﹣ x2+1.
(ii)证明:根据题意,画出图象如图所示:
设点P的坐标为(x,﹣ x2+1)则点Q的坐标为(x,2),D(x,0).
∴PD=|﹣ x2+1|,OD=|x|,QP=2﹣(﹣ x2+1)= x2+1.
在Rt△OPD中,依据勾股定理得:OP= = = x2+1.
∴OP=PQ
【点睛】本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、一元二次方程根的判别式、勾股定理等知识点.在(1)中求得二次函数的顶点坐标是解题的关键,在(Ⅱ)①中取k的特殊值得到关于a、b的二元一次方程组,求得a、b的值是解题的关键,在②中用P点的坐标分别表示出PD、OP的长是解题的关键.
24.(1)(,)
(2)销售单价为元,最大利润为元
【分析】本题考查了待定系数法求一次函数解析式,解二元一次方程组,二次函数的应用,正确列出等量关系是解题的关键.
(1)设y与x的函数表达式为,根据题意列出二元一次方程组求解即可得出y与x的函数表达式,再根据销售量与销售单价即可求得自变量的取值范围;
(2)根据题意列出利润的表达式,将其配方为顶点式,即可求解,需要注意的是销售单价是否满足其取值范围.
【详解】(1)解:设y与x的函数表达式为:,
由题可得,
解得:,
,,,
,,
与x的函数表达式为(,);
(2)解:由题可得:利润单个销售利润销售量,
总利润,
当时,有最大利润为元,
此该商品的销售单价为元,此时的最大利润为元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为,两侧距地面高处各有一盏灯,两灯间的水平距离为,则这个门洞内部顶端离地面的距离为( )
A. B.8 C. D.
2.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
3.在同一直角坐标系中与图象大致为
A. B. C. D.
4.如图,矩形OABC,点A的坐标为,AB=1.若抛物线与矩形OABC的边界总有两个公共点,则实数c的取值范围是( ).
A.c>8或c<-1 B.-1<c<8 C.c>1或c<-8 D.-8<c<1
5.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价,设平均每次降价的百分率为,降价后的价格为y元,原价为a元,则y与x的函数关系为( )
A. B. C. D.
6.如图所示,某大学的楼门是一抛物线形水泥建筑物,大门的地面宽度为,两侧距离地面高处各有一个挂校名横匾用的铁环,两铁环的水平距离为,则校门的高约为(精确到,水泥建筑物的厚度忽略不计)( )
A.9.2m B.9.1m C.9.0m D.8.9m
7.发射一枚炮弹,经过x秒后炮弹的高度为y米,x,y满足y=ax2+bx,其中a,b是常数,且a≠0.若此炮弹在第6秒与第14秒时的高度相等,则炮弹达到最大高度的时刻是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
8.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的图象大致是( ).
A. B. C. D.
9.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
A. B. C. D.
10.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
11.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
12.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
二、填空题
13.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.若球能越过球网,又不出边界,则h的取值范围为 .
14.数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) 100 110 120 130 …
月销量(件) 200 180 160 140 …
已知该运动服的进价为每件60元,设售价为x(x≥100)元,则月销量是 件,销售该运动服的月利润为 元(用含x的式子表示).
15.如图,抛物线y=x2﹣2x﹣3交x轴于A(﹣1,0)、B(3,0),交y轴于C(0,﹣3),M是抛物线的顶点,现将抛物线沿平行于y轴的方向向上平移三个单位,则曲线CMB在平移过程中扫过的面积为 (面积单位).
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,则经过 s后,飞机停止滑行.
17.抛物线的顶点为,已知一次函数的图象经过点,则这个一次函数图象与两坐标轴所围成的三角形面积为 .
三、解答题
18.设抛物线经过A(-1,2),B(2,-1)两点,且与轴相交于点M.
(1)求和(用含的代数式表示);
(2)求抛物线上横坐标与纵坐标相等的点的坐标;
(3)在第(2)小题所求出的点中,有一个点也在抛物线上,试判断直线AM和轴的位置关系,并说明理由.
19.阅读材料:如图的三个顶点分别作出与水平线垂直的三条直线,外侧的两条平行线之间的距离叫做的“水平宽”,中间的这条直线在内部的线段的长度叫做的“铅垂高”,我们可以得到一种计算三角形面积的新方法:,即三角形的面积等于水平宽与铅垂高的乘积的一半.
解决下面的问题:
如图(2)已知抛物线过点三点,
(1)求抛物线的解析式.
(2)若为第三象限抛物线上的动点,其横坐标为,的面积为,求关于的解析式,并求的最大值.
20.如图,已知抛物线经过三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点P是直线l上的一个动点,当的周长最小时,求点P的坐标;
(3)点M也是直线l上的动点,且为等腰三角形,请直接写出所有符合条件的点M的坐标.
21.如图1,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A,B.与y轴交于点C.连接AC,BC.已知△ABC的面积为2.
(1)求抛物线的解析式;
(2)平行于x轴的直线与抛物线从左到右依次交于P,Q两点.过P,Q向x轴作垂线,垂足分别为G,H.若四边形PGHQ为正方形,求正方形的边长;
(3)如图2,平行于y轴的直线交抛物线于点M,交x轴于点N (2,0).点D是抛物线上A,M之间的一动点,且点D不与A,M重合,连接DB交MN于点E.连接AD并延长交MN于点F.在点D运动过程中,3NE+NF是否为定值?若是,求出这个定值;若不是,请说明理由.
22.如图,在平面直角坐标系中,平行四边形的边与y轴交于E点,F是的中点,B、C、D的坐标分别为.
(1)求过B、E、C三点的抛物线的解析式;
(2)试判断抛物线的顶点是否在直线上;
(3)设过F与平行的直线交y轴于Q,M是线段之间的动点,射线与抛物线交于另一点P,当的面积最大时,求P的坐标.
23.已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
24.已知某商品的销售量y(单位:件)与销售单价x(单位:元)之间有下了关系:当销售单价为20元时,卖出100件;当销售单价为15元时,卖出150个,该商品的进价为10元;
(1)求y与x的函数表达式,并指出自变量的取值范围;
(2)商家要尽快清空库存并要赚取最大利润,求此该商品的销售单价与此时的最大利润.
《2.4二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A D D B B B A B
题号 11 12
答案 D D
1.D
【分析】建立直角坐标系,得到二次函数,门洞高度即为二次函数的顶点的纵坐标.
【详解】解:如图,以地面为x轴,门洞中点为O点,画出y轴,建立直角坐标系,
由题意可知各点坐标为,,,
设抛物线解析式为把B、D两点带入解析式,
∴,解得:,
∴解析式为,则,
所以这个门洞内部顶端离地面的距离为,
故选D.
【点睛】本题考查二次函数的简单应用,能够建立直角坐标系解出二次函数解析式是本题关键.
2.C
【分析】根据已知得出直角坐标系,进而求出二次函数的解析式,再把代入抛物线的解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过顶点,则通过画图可得知为原点,
由平面直角坐标系可知,,即,
设抛物线的解析式为,
将点代入得:,解得,
则抛物线的解析式为,即,
当时,,
所以水面下降,
故选:C.
【点睛】本题主要考查了二次函数的应用,根据已知建立平面直角坐标系从而得出二次函数的解析式是解决问题的关键.
3.A
【分析】本题由一次函数图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
【详解】解:A、由抛物线可知,,,由直线可知,,,故本选项正确;
B、由抛物线可知,,,由直线可知,,,故本选项错误;
C、由抛物线可知,,,由直线可知,,,故本选项错误;
D、由抛物线可知,,,由直线可知,,,故本选项错误.
故选A.
【点睛】本题考查了一次函数和二次函数的图象解答该题时,一定要熟记一次函数、二次函数的图象的性质.
4.D
【分析】求得抛物线经过点A时的c的值,然后根据图象即可求得.
【详解】解:矩形OABC,点A的坐标为(2,0),AB=1,
∴OC=AB=1,
把A(2,0)代入y=2x2+c得,0=8+c,解得c= 8,
由图象可知, 8<c<1,故D正确.
故选:D.
【点睛】本题考查了二次函数图形与系数的关系,二次函数图象上点的坐标特征,矩形的性质,数形结合是解题的关键.
5.D
【详解】∴第一次降价后的价格是a×(1 x),
第二次降价为a×(1 x)×(1 x)=a(1 x)2
∴y=a(1 x)2.
故选D.
6.B
【分析】由题意可知,以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,抛物线过(0,0)、(8,0)、(1、4)、(7、4),运用待定系数法求出解析式后,求函数值的最大值即可.
【详解】解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,
则抛物线过O(0,0)、E(8,0)、A(1、4)、B(7、4)四点,
设该抛物线解析式为:y=ax2+bx+c,
则,
解得:.
.
故函数解析式为:y=-x2+x.
当x=4时,可得y=-≈9.1米,
故选B.
【点睛】本题考查点的坐标的求法及二次函数的实际应用关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标.
7.B
【详解】试题分析:由于炮弹在第6s与第14s时的高度相等,即x取6和14时y的值相等,根据抛物线的对称性可得到抛物线y=ax2+bx的对称轴为直线x="6+" =10,然后根据二次函数的最大值问题求解.
∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时间是10s.
故选B.
考点:二次函数的应用.
8.B
【分析】分别求出当时,时和时S关于t的函数解析式,再根据解析式判断函数图象即可.
【详解】解:由题意得:AB,
当时,点P在AC上,点Q在AB上,
则AP=AC-CP=4-2t,AQ=AB-BQ=5-2.5t,
如图,过点Q作QM⊥AC于M,
∴sin∠A=,即,
∴,
此时,
当时,点P在AB上,点Q在AC上,
则AP=2t-4,AQ=2.5t-5,
如图,过点P作PN⊥AC于N,
同理可得:,
此时,
∵二次函数的图象开口向上,对称轴为,
∴当时,函数图象为二次函数的图象的一部分,
当时,点Q与点C重合,点P在AB上,
此时,
∴当时,函数图象为直线的一部分,
故选:B.
【点睛】此题考查了动点问题的函数图象,正确表示出的面积并能够根据函数解析式选择相应的函数图象是解题的关键.
9.A
【分析】利用顶点式求得抛物线的解析式,再令x=0,求得相应的函数值,即为所求的答案.
【详解】解:由题意可知点(1,3)是抛物线的顶点,
∴设这段抛物线的解析式为y=a(x-1)2+3.
∵该抛物线过点(3,0),
∴0=a(3-1)2+3,
解得:a=-.
∴y=-(x-1)2+3.
∵当x=0时,y=-(0-1)2+3=-+3=,
∴水管应长m.
故选:A
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法及二次函数的相关性质是解题的关键.
10.B
【分析】设每月所获利润为w,按照等量关系列出二次函数,并根据二次函数的性质求得最值即可.
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
【点睛】本题考查了二次函数在实际生活中的应用,根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键.
11.D
【分析】将函数关系式转化为顶点式,然后利用开口方向和顶点坐标即可求出最多的利润.
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
【点睛】此题考查的是利用二次函数求最值,掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键.
12.D
【分析】设每件降价x元,由“每降低5元,每天可多售出10件”可知每降价1元可多售2件,根据题意可知每天的利润为(20+2x)(40-x),据此一一判断选项即可.
【详解】因为每降低5元,每天可多售出10件,所以每降价1元可多售2件,
设每件降价x元,每天的利润为y元,则每天可售(20+2x)件,每件利润为40-x,
所以每天的利润为
将整理成顶点式有,
由顶点式可知当销售单价降低15元时,每天获得利润最大,每天的最大利润为1250元,故A、B正确;
将x=10代入到解析式中解得y=1200,故C正确;
令y=1050,则,解得,即当每天的利润为1050元,则销售单价可能降低了5元,也可能降低了25元,所以D错误;
综上所述,答案选D.
【点睛】本题考查的是二次函数的实际应用,能够根据题意列出每天利润与降低单价的二次函数方程是解题的关键.
13.
【分析】把点A坐标代入y=a(x﹣6)2+h得y=(x﹣6)2+h,当x=9时,y>2.43,求出h取值范围,当x=18时,y≤0,求出h取值范围,综合即可求解.
【详解】解:点A(0,2),将点A的坐标代入抛物线表达式得:2=a(0﹣6)2+h,
解得:a=,
∴抛物线的表达式为y=(x﹣6)2+h,
由题意得:当x=9时,y=(x﹣6)2+h=(9﹣6)2+h>2.43,
解得:h>;
当x=18时,y=(x﹣6)2+h=(18﹣6)2+h≤0,
解得:h≥,
故h的取值范围是h≥.
故答案为:
【点睛】此题主要考查了二次函数的应用题,根据题意得到两个不等式并求出不等式组的解集是解题关键.
14.
【详解】分析:运用待定系数法求出月销量;根据月利润=每件的利润×月销量列出函数关系式.
详解:设月销量y与x的关系式为y=kx+b,
由题意得,,
解得.
则y=-2x+400;
由题意得,y=(x-60)(-2x+400)
=-2x2+520x-24000
点睛:本题考查的是二次函数的应用,一次函数的运用,掌握待定系数法求函数解析式是解题的关键.
15.9
【分析】由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积,求得四边形OCBD的面积即可.
【详解】解:如图所示,连接BC,OD,
由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积,
根据题意可得:OB=3,OC=3,BD=3,
所以,曲线CMB在平移过程中扫过的面积=OC×OB+ OB×BD=×3×3+×3×3=9.
故答案为:9.
【点睛】本题考查了二次函数图象与几何变换,由图象可知曲线CMB在平移过程中扫过的面积=平行四边形OCBD的面积是解题的关键.
16.25
【分析】要求飞机从滑行到停止的路程,即求出函数取最大值时,t的值即可,因此将函数化为顶点式即可.
【详解】解:
所以当t=25时,该函数有最大值625
即第25秒时,飞机滑行最大距离625m停下来,
故答案为:25.
【点睛】本题主要考查了二次函数的应用,掌握二次函数求最值的方法,即公式法或配方法是解题关键.
17.1
【分析】易得顶点(2,-6),根据待定系数法,求出一次函数解析式,进而求出直线与坐标轴的交点,根据三角形的面积公式,即可求解.
【详解】∵抛物线,
∴顶点(2,-6),
∵一次函数的图象经过点,
∴,解得:k=,
∴一次函数解析式为:,
∴直线与坐标轴的交点坐标分别是:(0,3),(,0),
∴一次函数图象与两坐标轴所围成的三角形面积=.
故答案是:1.
【点睛】本题主要考查二次函数和一次函数图象与平面几何的综合,掌握一次函数图象与坐标轴的交点坐标的求法,是解题的关键.
18.(1);(2)(1,1),(-2,-2);(3)点(1,1)在抛物线时,直线AM∥轴;点(-2,-2)在抛物线时,直线AM与轴相交
【分析】(1)把A(-1,2),B(2,-1)两点分别代入抛物线y=ax2+bx+c,即可用a表示出b、c的值;(2)把(1)中所求b、c的值及x=y代入抛物线y=ax2-bx+c-1,即可求出符合条件的点的坐标;(3)把(2)中所求的两点分别代入(1)中抛物线的解析式,即可求出未知数的值,从而求出其解析式,根据其解析式可求出函数图象与y轴的交点坐标,根据其纵坐标与A点纵坐标的关系即可判断出直线AM与x轴的关系.
【详解】(1)∵抛物线y=ax2+bx+c经过A(-1,2),B(2,-1)两点,
∴,
解得.
(2)∵横坐标与纵坐标相等
∴由(1)得,抛物线y=ax2-bx+c-1的解析式是y=ax2+(a+1)x-2a=x,
即ax2+ax-2a=0,
∵a是抛物线解析式的二次项系数,
∴a≠0,
∴x2+x-2=0,
解得:x1=1,x2=-2,
∴抛物线y=ax2-bx+c-1满足条件的点的坐标是P1(1,1),P2(-2,-2).
(3)由(1)得抛物线y=ax2+bx+c的解析式是y=ax2-(a+1)x+1-2a,
①当P1(1,1)在抛物线上时,有a-(a+1)+1-2a=1,
解得a=-,
∴抛物线y=ax2+bx+c的解析式是y=-x2-x+2,它与y轴的交点是M(0,2)
∵点A(-1,2),M(0,2)两点的纵坐标相等,
∴直线AC平行于x轴.
②当P2(-2,-2)在抛物线上时,有4a+2(a+1)+1-2a=-2,
解得a=-,
∴抛物线的解析式为y=-x2+x+,它与y轴的交点是C(0,),
∵A、M两点的纵坐标不相等,
∴直线AM与x轴相交,
综上所述,当点(1,1)在抛物线y=ax2+bx+c上时,直线AM// x轴;当点(-2,-2)在抛物线y=ax2+bx+c上时,直线AM与x轴相交.
【点睛】本题考查了用代入法求函数解析式,抛物线上点的坐标特征.第(3)小题要将(2)中所求点代入解析式进行分类讨论.
19.(1);(2),4
【分析】(1)根据题意,可设出抛物线解析式,代入A、B、C点的坐标,即可得出抛物线的解析式;
(2)根据待定系数法得出直线AB的解析式为,由题意可得即可求解.
【详解】解:由题可设抛物线解析式为,
且已知抛物线过点,
将其带入可得
解得
则抛物线解析式为.
由点可得直线的解析式为,
由题意可得
.
则可得当时,
有最大值为.
【点睛】此题主要考查二次函数在给定区间上的最值、二次函数综合题、待定系数法求二次函数解析式,熟练掌握二次函数的图象和性质是解题关键.
20.(1);(2)(1,﹣2);(3)(1,﹣)或(1,)或(1,﹣1)或(1,0)
【分析】(1)根据点A、B、C的坐标,利用待定系数法求解抛物线的函数解析式即可;
(2)因为AC为定值,要使的周长最小,只需PA+PC最小即可,根据抛物线的对称性,连接BC交l于点P,此时PA+PC最小为BC的长,由点B、C坐标求出直线BC的函数解析式,利用二次函数的性质和一次函数图像上的点的坐标特征即可求得点P坐标;
(3)设点M(1,m),分AM=AC、AM=MC、AC=MC三种情况讨论求解即可.
【详解】解:(1)将点代入中,
得:,解得:,
∴抛物线的函数关系式为;
(2)因为AC为定值,要使的周长最小,只需PA+PC最小即可,
连接BC交l于点P,此时PA+PC取得最小值,如图,
设直线AB的函数解析式为y=kx+t(k≠0),
将代入,
得:,解得:,
∴直线BC的函数解析式为y=x﹣3,
∵,
∴抛物线的对称轴为直线x=1,即点P的横坐标为1,
将x=1代入y=x﹣3中,得:y=1﹣3=﹣2,
∴点P坐标为(1,﹣2);
(3)设点M(1,m),则,,
,
分三种情况讨论:
①当AM=AC时,有=10,
解得:,
∴点M的坐标为(1,﹣)或(1,);
②当AM=MC时,有=,
解得:m=﹣1,
∴点M的坐标为(1,﹣1);
③当AC=MC时,有10=,
解得:,
∴点M的坐标为(1,0)或(1,﹣6),
设直线AC的函数解析式为y=px+q,
将代入,
得:,解得:,
∴直线AC的函数解析式为y=﹣3x﹣3,
∵当x=1时,y=﹣3﹣3=﹣6,
∴点M(1,﹣6)在直线AC上,即点A、C、M不能组成三角形,
故满足题意的点M的坐标为(1,﹣)或(1,)或(1,﹣1)或(1,0).
【点睛】本题考查了待定系数法求二函数的解析式、求一次函数的解析式、轴对称中的最短路径问题、图像上点的坐标特征、两点间的距离公式以及等腰三角形的性质,解答的关键是认真审题,寻找相关联的信息,利用待定系数法、数形结合和分类讨论的思想方法进行推理、探究和计算.
21.(1);(2)或;(3)是,3NE+NF为定值4
【分析】(1)先将抛物线解析式变形,可得A和B的坐标,从而得AB=1+3=4,根据三角形ABC的面积为2可得OC的长,确定点C的坐标,根据点C的坐标,利用待定系数法即可求出二次函数的解析式;
(2)设点P的纵坐标为m,当y=m时,﹣x2+x+1=m,解方程可得P和Q两点的坐标,从而得G和H的坐标,再利用正方形的性质可得出关于m的方程,解之即可得出结论;
(3)设点D(n,﹣n2+n+1),利用待定系数法求直线AD和BD的解析式,表示FN和OK的长,直接代入计算可得结论.
【详解】(1)如图1,y=ax2﹣2ax﹣3a=a(x2﹣2x﹣3)=a(x﹣3)(x+1),
∴A(﹣1,0),B(3,0),
∴AB=4,
∵△ABC的面积为2,即,
∴OC=1,
∴C(0,1),
将C(0,1)代入y=ax2﹣2ax﹣3a,得:﹣3a=1,
∴a=﹣,
∴该二次函数的解析式为y=﹣x2+x+1;
(2)如图2,设点P的纵坐标为m,当y=m时,﹣x2+x+1=m,
解得:x1=1+,x2=1﹣,
∴点P的坐标为(1﹣,m),点Q的坐标为(1+,m),
∴点G的坐标为(1﹣,0),点H的坐标为(1+,0),
∵矩形PGHQ为正方形,
∴PQ=PG,
∴1+﹣(1﹣)=m,
解得:m1=﹣6﹣2,m2=﹣6+2,
∴当四边形PGHQ为正方形时,边长为6+2或2﹣6;
(3)如图3,设点D(n,﹣n2+n+1),延长BD交y轴于K,
∵A(﹣1,0),
设AD的解析式为:y=kx+b,
则,解得:,
∴AD的解析式为:y=(﹣)x﹣,
当x=2时,y=﹣n+2﹣n+1=﹣n+3,
∴F(2,3﹣n),
∴FN=3﹣n,
同理得直线BD的解析式为:y=(﹣)x+n+1,
∴K(0,n+1),
∴OK=n+1,
∵N(2,0),B(3,0),
∴,
∵EN∥OK,
∴,
∴OK=3EN,
∴3EN+FN=OK+FN=n+1+3﹣n=4,
∴在点D运动过程中,3NE+NF为定值4.
【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、正方形的性质、待定系数法求一次函数解析式以及平行线分线段成比例定理等知识,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用正方形的性质,找出关于m的方程;(3)利用AD和BD的解析式确定FN和OK的长,可解决问题.
22.(1);(2)顶点是在直线上,理由见解析;(3)P点坐标为(9,).
【分析】(1)先求出A点坐标,再求出直线AB的解析式,进而求得E的坐标,然后用待定系数法解答即可;
(2)先求出点F的坐标,再求出直线EF的解析式,然后根据抛物线的解析式确定顶点坐标,然后进行判定即可;
(3)设P点坐标为(p,),求出直线BP的解析式,进而求得M的坐标;再求FQ的解析式,确定Q的坐标,可得|MQ|=+6,最后根据S△PBQ= S△MBQ+ S△PMQ列出关于p的二次函数并根据二次函数的性质求最值即可.
【详解】解:(1)∵平行四边形,B、C、D的坐标分别为
∴A(3,10),
设直线AB的解析式为y=kx+b,
则 ,解得,
∴直线AB的解析式为y=2x+4,
当x=0时,y=4,则E的坐标为(0,4),
设抛物线的解析式为:y=ax2+bx+c,
,解得,
∴过B、E、C三点的抛物线的解析式为;
(2)顶点是在直线上,理由如下:
∵F是的中点,
∴F(8,10),
设直线EF的解析式为y=mx+n,
则,解得,
∴直线EF的解析式为y=x+4,
∵,
∴抛物线的顶点坐标为(3,),
∵=×3+4,
∴抛物线的顶点是否在直线上;
(3)∵,则设P点坐标为(p,),直线BP的解析式为y=dx+e,
则 ,解得,
∴直线EF的解析式为y=,
当x=0时,y=,则M点坐标为(0,),
∵AB//FQ ,
∴设FQ的解析式为y=2x+f,则10=2×8+f,解得f=-6,
∴FQ的解析式为y=2x-6 ,
∴Q的坐标为(0,-6),
∴|MQ|=+6,
∴S△PBQ= S△MBQ+ S△PMQ
=
=
=
=
∴当p=9时,的面积最大时,
∴P点坐标为(9,).
【点睛】本题主要考查了运用待定系数法求函数解析式、二次函数求最值等知识点,灵活求得所需的函数解析式成为解答本题的关键.
23.(Ⅰ)a=﹣;(Ⅱ)(i)y=﹣ x2+1;(ii)证明见解析.
【分析】(1)可用a表示出抛物线的顶点坐标,再代入直线方程可求得a的值,
(2)(i)由于k为任意非零实数,可取k=1和k=2,再联立两解析式消去y,得到的一元二次方程有两个相等的实数根可得到两个关于a、b的方程,可求得a、b的值,即可求得拋物线解析式; (ii)设出P点坐标,连接OP,过P作PQ⊥直线y=2,作PD⊥x轴于点D,可分别表示出OP和PQ,可证明其相等
【详解】解:(1)将k=1,b=1代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x.
∵y=ax2+x+1=a(x+ )2+1﹣ ,
∴抛物线的顶点为(﹣ ,1﹣ ).
∵抛物线的顶点在直线y=x上,
∴﹣ =1﹣ ,
解得:a=﹣ .
(2)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1.
∵无论非零实数k取何值,直线与抛物线都只有一个交点,
∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根,
∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0.
∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立,
∴4a+1=0且b=0,
∴a=﹣ ,b=0.
∴抛物线的解析式为y=﹣ x2+1.
(ii)证明:根据题意,画出图象如图所示:
设点P的坐标为(x,﹣ x2+1)则点Q的坐标为(x,2),D(x,0).
∴PD=|﹣ x2+1|,OD=|x|,QP=2﹣(﹣ x2+1)= x2+1.
在Rt△OPD中,依据勾股定理得:OP= = = x2+1.
∴OP=PQ
【点睛】本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、一元二次方程根的判别式、勾股定理等知识点.在(1)中求得二次函数的顶点坐标是解题的关键,在(Ⅱ)①中取k的特殊值得到关于a、b的二元一次方程组,求得a、b的值是解题的关键,在②中用P点的坐标分别表示出PD、OP的长是解题的关键.
24.(1)(,)
(2)销售单价为元,最大利润为元
【分析】本题考查了待定系数法求一次函数解析式,解二元一次方程组,二次函数的应用,正确列出等量关系是解题的关键.
(1)设y与x的函数表达式为,根据题意列出二元一次方程组求解即可得出y与x的函数表达式,再根据销售量与销售单价即可求得自变量的取值范围;
(2)根据题意列出利润的表达式,将其配方为顶点式,即可求解,需要注意的是销售单价是否满足其取值范围.
【详解】(1)解:设y与x的函数表达式为:,
由题可得,
解得:,
,,,
,,
与x的函数表达式为(,);
(2)解:由题可得:利润单个销售利润销售量,
总利润,
当时,有最大利润为元,
此该商品的销售单价为元,此时的最大利润为元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
