3.3垂径定理同步强化练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
3.3垂径定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
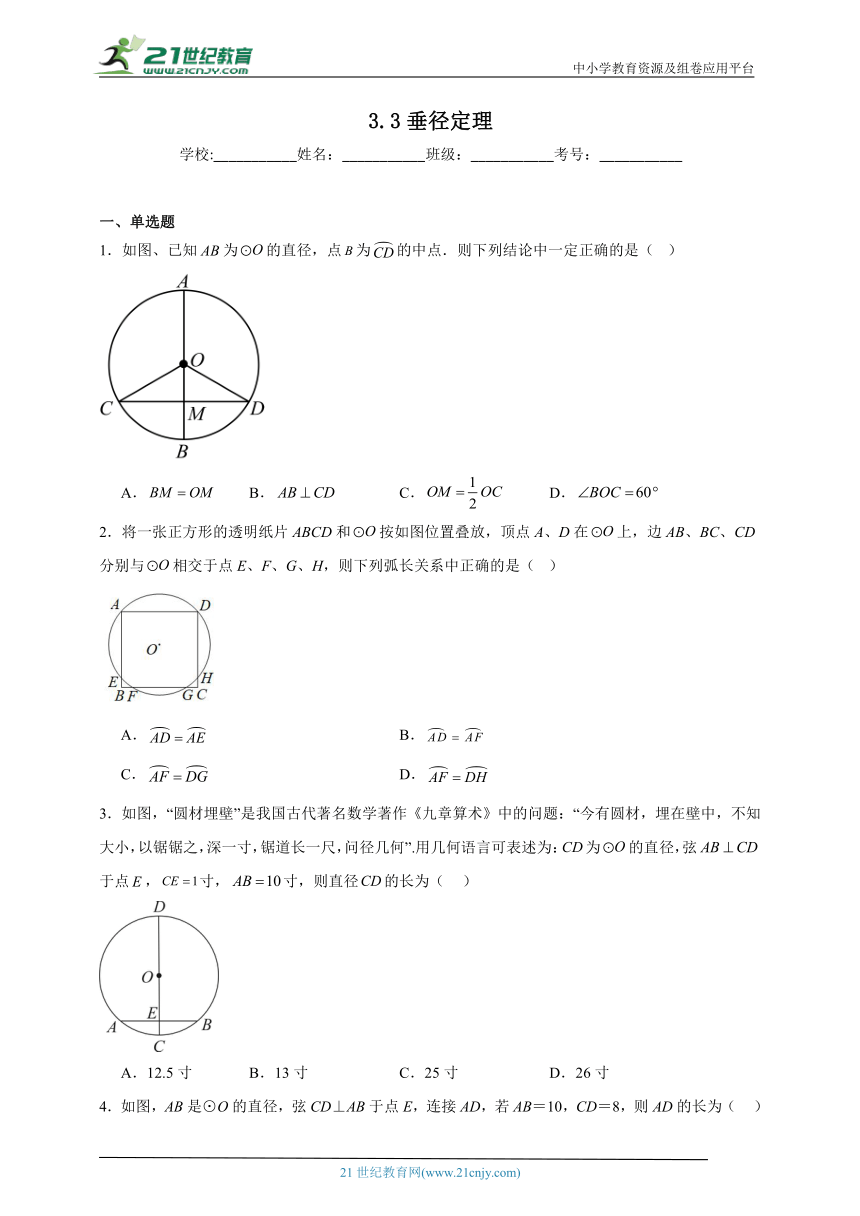
1.如图、已知为的直径,点为的中点.则下列结论中一定正确的是( )
A. B. C. D.
2.将一张正方形的透明纸片ABCD和按如图位置叠放,顶点A、D在上,边AB、BC、CD分别与相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B.
C. D.
3.如图,“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”.用几何语言可表述为:为的直径,弦于点,寸,寸,则直径的长为( )
A.12.5寸 B.13寸 C.25寸 D.26寸
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( )
A.8 B.2 C.3 D.4
5.《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,为的直径,弦于,寸,寸,求直径的长.”则
A.寸 B.寸 C.寸 D.寸
6.如图,在⊙O中,半径OC⊥AB于点E,AE=2,则下列结论正确的是( )
A. B.
C.垂直平分 D.垂直平分
7.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
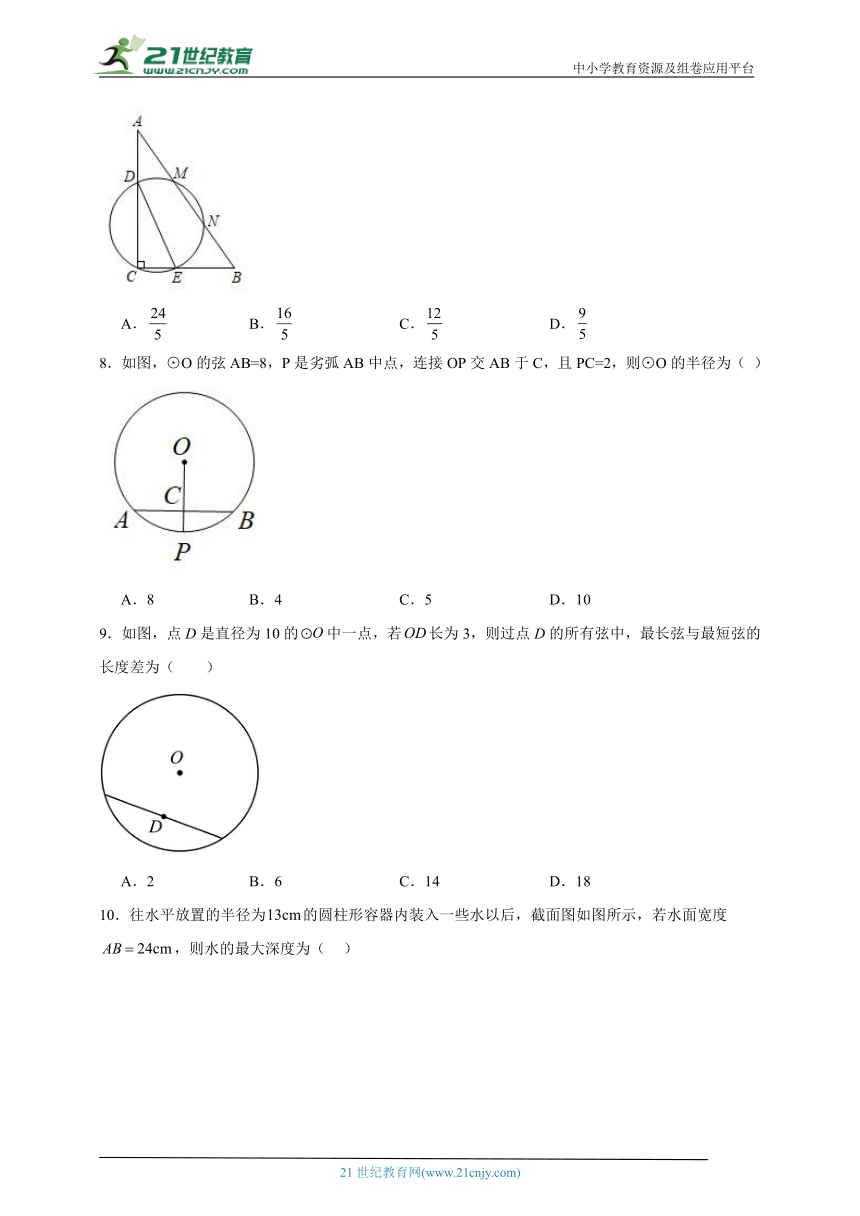
8.如图,⊙O的弦AB=8,P是劣弧AB中点,连接OP交AB于C,且PC=2,则⊙O的半径为( )
A.8 B.4 C.5 D.10
9.如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A.2 B.6 C.14 D.18
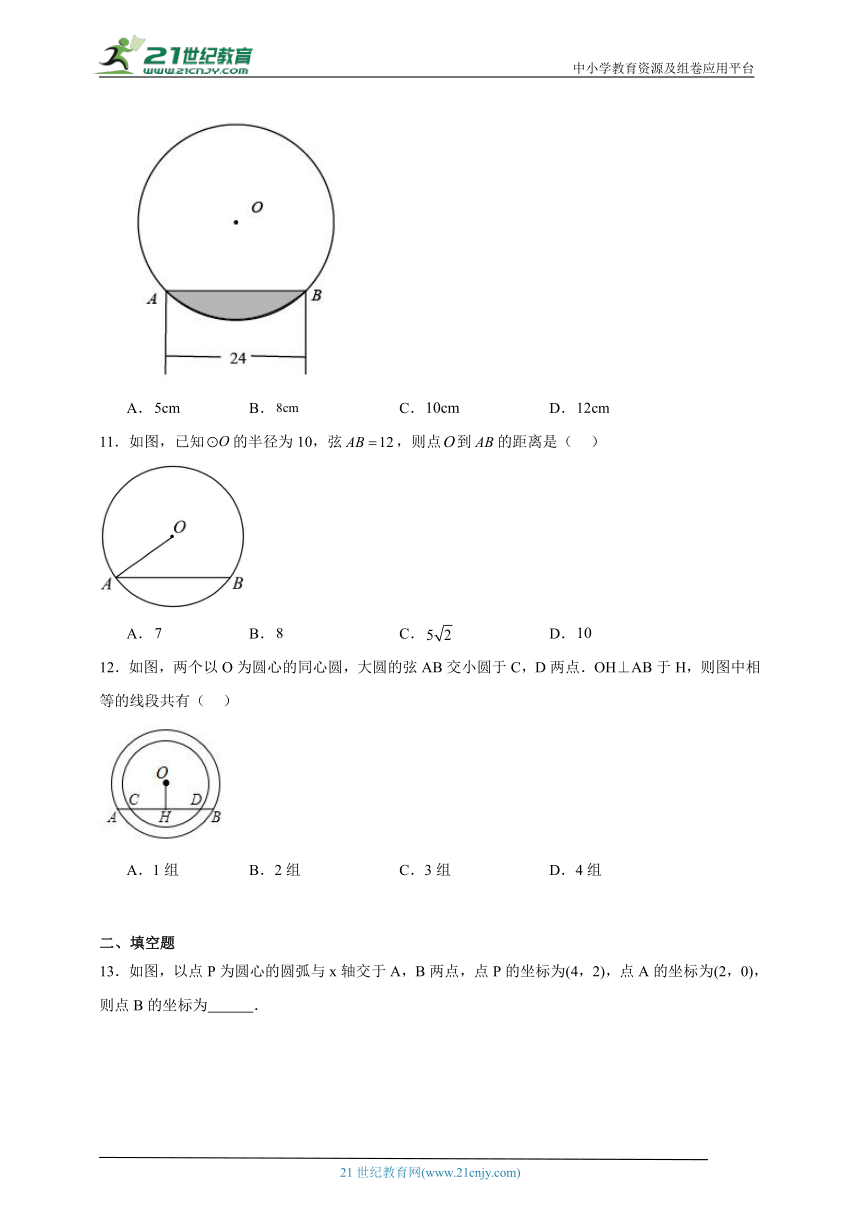
10.往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,则水的最大深度为( )
A. B. C. D.
11.如图,已知的半径为10,弦,则点到的距离是( )
A. B. C. D.
12.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组 B.2组 C.3组 D.4组
二、填空题
13.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为 .
14.如图,以O为圆心的两个同心圆,过点的直径与外圆交于C,D两点,若CE=8,ED=2,则AB长 时,外圆的弦AB与内圆相切于点E.
15.如图,半圆O的直径AB=4cm,,点C是上的一个动点(不与点B,G重合),CD⊥OG于点D,CE⊥OB于点E,点E与点F关于点O中心对称,连接DE、DF,则△DEF面积的最大值为 cm2
16.已知的半径为2,弦,是上一点,且,直线与交于点,则的长为 .
17.如图,在△ABC中,∠ACB=90°,以C为圆心,CA长为半径的圆交AB于D,若AC=6,BC=8,则AD= .
三、解答题
18.如图,点P的坐标为(4,0),⊙P的半径为5,且⊙P与x轴交于点A、B,与y 轴交于点C、D,试求出点A、B、C、D的坐标.
19.点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.
20.如图是一个管道的横截面,圆心到水面的距离是3,水面宽.
(1)求这个管道横截面的半径.
(2)求的度数.
21.已知,⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC.
求证:AC2=AEAB.
22.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
23.如图,P是⊙O外一点,PA交⊙O于点B,PD交⊙O于点C,且∠APO=∠DPO. 弦AB与CD相等吗?为什么?
24.如图,在半径为的中,弦长.求:
(1)的度数;
(2)点O到的距离.
《3.3垂径定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D C D A C A B
题号 11 12
答案 B D
1.B
【分析】本题考查了垂径定理及其推论,根据垂径定理中“知二推三”进行推理论证,即可解题.
【详解】解:为的直径,点为的中点.
,
故选:B.
2.C
【分析】连接,根据弦与弧的关系,只要比较弦长即可比较弧长的大小即可求解.
【详解】如图,连接,过点作,交于,交于,则,
四边形是正方形,
,,
,
四边形是矩形,
,
,
,
,
,
A. ,,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. ,,故该选项正确,符合题意;
D.,,故该选项不正确,不符合题意;
故选:C.
【点睛】本题考查了弦与弧的关系,掌握同圆或等圆中,等弦对等弧是解题的关键.
3.D
【分析】连接,根据垂径定理,设直径为寸,利用列方程即可.
【详解】解:连接,
设直径的长为寸,则半径寸,
∵为⊙O的直径,弦于E,寸,
∴ ,
根据勾股定理得,
解得,
(寸).
故选:D.
【点睛】本题考查了垂径定理和勾股定理;熟练掌握垂径定理,由勾股定理得出方程是解决问题的关键.
4.D
【分析】如图,连接OD,利用勾股定理求出OE,再利用勾股定理求出AD即可.
【详解】解:如图,连接OD.
∵AB⊥CD,
∴CE=ED=4,
∵∠OED=90°,OD=5,
∴OE===3,
∴AE=OA+OE=8,
∴AD===4,
故选:D.
【点睛】本题考查垂径定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.C
【分析】连接AO,根据垂径定理及勾股定理即可求出半径,即可求出CD的长.
【详解】如图,连接AO,设AO=OD=r,
故OE=r-1,
∵AB=10,∴AE=5,
由AO2=AE2+OE2,即r2=52+( r-1)2,
解得r=13,故CD=2r=26
故选C
【点睛】此题主要考查垂径定理,解题的关键是根据勾股定理进行求解.
6.D
【分析】由垂径定理和勾股定理分别对各个选项进行判断即可.
【详解】解:连接OA,
条件不足,不能求出OE和EC的长,故选项A、B不符合题意;
∵OC⊥AB于点E,
∴OC是线段AB的垂直平分线,故选项D正确,符合题意;
选项C不符合题意,
故选:D.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
7.A
【分析】由题意可知,C、O、G三点在一条直线上OG最小,MN最大,再由勾股定理求得AB,然后由三角形面积求得CF,最后由垂径定理和勾股定理即可求得MN的最大值.
【详解】解:如图,过O作OG⊥AB于G,连接OC、OM,
∵DE=6,∠ACB=90°,OD=OE,
∴OC=DE=3,
∵OM=3,
∴只有OG最小,GM才能最大,从而MN有最大值,
∴只有C、O、G三点在一条直线上OG最小,
过C作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10,
∵AC BC=AB CF,
∴CF=,
∴OG=CF OC=,
∴MG==,
∴MN=2MG=
故选:A
【点睛】本题考查了勾股定理,垂线段最短,垂径定理等知识,正确作出辅助线,得出C、O、G三点在一条直线上OG最小是解题的关键.
8.C
【详解】解:连接OA,
∵P是劣弧AB中点,
∴OP⊥AB,AC=AB=×8=4,
设⊙O的半径为x,
则OC=OP﹣PC=x﹣2,
在Rt△OAC中,
OA2=OC2+AC2,
∴x2=42+(x﹣2)2,
解得:x=5,
∴⊙O的半径为5.
故选C.
9.A
【分析】要满足最短弦,只需满足垂直于该弦,再用垂径定理和勾股定理求得最短弦,由过点D的所有弦中,最长弦是直径,即可得到答案.
【详解】解:根据题意可知,要满足最短弦,只需满足垂直于该弦,设该最短弦是,如图,于点D,
∴,,
∴,
∴,
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为,
故选:A
【点睛】此题考查了垂径定理、勾股定理等知识,熟练掌握过圆内一点的最长弦和最短弦是解题的关键.
10.B
【分析】连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出CD的长.
【详解】解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,
∵OC⊥AB,由垂径定理可知,
∴AC=CB=AB=12,
在Rt△AOC中,由勾股定理可知:
∴,
∴,
故选:B.
【点睛】本题考查了垂径定理及勾股定理的应用,属于基础题,关键是过O点作AB的垂线,由此即可求解.
11.B
【分析】过点作于点,由垂径定理可得,然后在中由勾股定理即可求出点到的距离.
【详解】解:过点作于点,如下图,
∵,,
∴,
∵的半径为10,即,
∴在中,,
即点到的距离是8.
故选:B.
【点睛】本题主要考查了垂径定理以及勾股定理的应用,理解并掌握垂径定理是解题关键.
12.D
【分析】先根据OH⊥AB于点H可知,AH=BH,CH=DH,故可得出AC=BD,AD=BC,进而可得出结论.
【详解】解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC=BD.
所以共有4组相等的线段.
故选:D.
【点睛】本题考查的是垂径定理,熟知垂直于弦的直径平分弦是解答此题的关键.
13.(6,0)
【详解】解:过点P作PM⊥AB于M,则M的坐标是(4,0)
∴MB=MA=4-2=2,
∴点B的坐标为(6,0)
14.8
【分析】连接OA,首先求得半径的长,则OE即可求解,然后在直角△OAE中,利用勾股定理即可求得AE的长,则AB即可求解.
【详解】连接OA,则圆的半径OA=,
则OE=5-2=3,
在直角△OAE中,AE=,
∴AB=2AE=8.
【点睛】本题考查了切线的性质以及垂径定理,正确求得AE的长是关键.
15.2
【分析】连接OC,设OD=x,OE=OF=y.根据S△DEF=×EF×OD=×2y×x=xy,当xy的值最大时,△DEF的面积最大;根据矩形的性质,通过判定四边形ODCE是矩形,得;根据勾股定理、完全平方公式的性质分析,可得结论.
【详解】连接OC,设OD=x,OE=OF=y.
∵
∴OG⊥AB,
∵S△DEF=×EF×OD=×2y×x=xy,
∴xy的值最大时,△DEF的面积最大,
∵CD⊥OG于点D,CE⊥OB于点E,
∴∠CEO=∠CDO=∠DOE=90°,
∴四边形ODCE是矩形,
∴
∴x2+y2=22,即x2+y2=4,
∵(x﹣y)2≥0,
∴x2+y2≥2xy,
∴2xy≤4,
∴xy≤2,
∴xy的最大值为2,
∴△DEF的面积的最大值为2 cm2
故答案为:2.
【点睛】本题考查了圆、勾股定理、中心对称、矩形、完全平方公式的知识;解题的关键是熟练掌握圆的对称性、勾股定理、完全平方公式的性质,从而完成求解.
16.1或3
【分析】根据垂径定理建立直角三角形,再运用勾股定理求得,进而分两种情况讨论即可.
【详解】如图,连接,
,由垂径定理可知,,,
则在中,,
或,
故答案为:1或3.
【点睛】本题考查了垂径定理,勾股定理计算圆周上点到弦得距离,熟练掌握基本定理,准确分类讨论是解题关键.
17.7.2.
【分析】作CE⊥AB于E,根据勾股定理求出AB,根据三角形的面积公式求出CE,根据勾股定理求出AE,根据垂径定理计算.
【详解】解:作CE⊥AB于E,
△ABC中,∠ACB=90°,
∴AB===10,
△ABC的面积=×AC×BC=×AB×CE,
∴6×8=10×CE,
解得,CE=4.8,
由勾股定理得,AE===3.6,
∵CE⊥AB,
∴AD=2AE=7.2.
故答案为:7.2.
【点睛】本题考查垂径定理,勾股定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
18.A(-1,10),B(9,0),C(0,3),D(0,-3)
【分析】先根据点P的坐标为(3,0),⊙P的半径为5结合勾股定理可得点C、点D的坐标,再根据⊙P的半径为5可得AO、PB的长,即可求得点A、点B的坐标.
【详解】解:∵点P的坐标为(3,0),⊙P的半径为5
∴OP=3,CO=DO=4
∴点C的坐标为(4,0),点D的坐标为(-4,0)
∵⊙P的半径为5
∴AO=2,PB=5
∴点A的坐标为(-2,0),OB=8
∴点B的坐标为(8,0).
【点睛】本题考查了勾股定理,垂径定理以及点的坐标,本题知识点多,综合性强,在中考中比较常见,在各种题型中均有出现,一般难度不大,需熟练掌握.
19.289或119
【分析】要求梯形的面积就要先求出梯形的高,然后利用梯形的面积公式计算;求梯形的高,先利用垂径定理和勾股定理求出圆心到梯形两底的距离,进而得到梯形的高,由此结合梯形的面积公式即可得到其面积.
【详解】
解:连接OA、OD,作OE⊥AB,OF⊥CD,垂足分别为E、F,在Rt△AOE中,OA=13,AE=12,OE==5;同理可得OF=12
分两种情况:如图1.EF=OF+OE=12+5=17
如图2.EF=OF-OE=12-5=7
因此梯形的面积为(AB+CD)EF=(24+10)EF=289或119.
故答案为289或119.
【点睛】本题考查面积计算,勾股定理,垂径定理及推论,注意本题需分情况求解梯形的面积,即分圆心在梯形的内部与外部两种情况求解.
20.(1)
(2)
【分析】(1)根据垂径定理,可知是等腰直角三角形,再根据勾股定理即可解;
(2)根据等腰直角三角形的性质即可得出答案.
【详解】(1)解:如图,连接,
是等腰直角三角形,
在中,
这个管道横截面的半径为.
(2)解:在等腰直角中,,
在等腰直角中,,
.
【点睛】本题考查了垂径定理、勾股定理、等腰直角三角形的性质,解题关键是熟练掌握垂径定理和勾股定理.
21.见解析
【分析】连接BC,根据垂径定理得到BC=AC,根据等边对等角得到∠CAB=∠CBA,∠CAB=∠ECA,证明△AEC∽△ACB,根据相似三角形的性质得到即可证明.
【详解】连接BC,
∵AB⊥CD,CD为⊙O的直径
∴BC=AC,
∴∠CAB=∠CBA
又EA=EC,
∴∠CAB=∠ECA
∴∠CBA=∠ECA
∴△AEC∽△ACB
即AC2=AEAB.
【点睛】考查垂径定理,等腰三角形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题的关键.
22.居民楼会受到噪声的影响,17.3s
【分析】过点A作AB⊥MN,利用锐角三角函数的定义求出AB的长与200m相比较即可;过点A作AD=OA=200m,求出OD的长即可得出居民楼受噪音影响的时间.
【详解】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3 s.
【点睛】本题是解直角三角形的应用,主要考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
23.AB=CD.
【分析】过O点分别作AB和CD的垂线,交点分别为E和F,连接AO和DO.由垂径定理可得OE和OF分别是AB和CD的垂直平分线;证明△PEO≌△PFO得OE=OF,再证△AEO≌△DFO得AE=DF即可.
【详解】解:AB=CD.
证明:过O点分别作AB和CD的垂线,交点分别为E和F,连接AO和DO,
∵∠OEP=∠OFP=90°,∠APO=∠DPO,PO=PO,
∴△PEO≌△PFO,
∴OE=OF,
∵OE为弦AB的垂线,OF为弦CD的垂线,
∴AE=EB,DF=CF,、
∵AO=DO,
∴△AEO≌△DFO,
∴AE=DF,
∴AB=2AE=2DF=CD,
即AB=CD.
【点睛】本题结合三角形全等综合考察了垂径定理的知识.
24.(1)60°;(2)25mm
【分析】(1)证明是等边三角形,从而可得结论;
(2)过点O作OC⊥AB,垂足为点C,利用垂径定理求解 再利用勾股定理可得答案.
【详解】解:(1)∵OA,OB是⊙O的半径,
∴OA=OB=50mm,
又∵AB=50mm,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=60°.
(2)过点O作OC⊥AB,垂足为点C,如图所示,
由垂径定理得AC=CB=AB=25mm,
在Rt△OAC中OC2=OA2-AC2=502-252=252×3,
∴OC==25(mm),
即点O到AB的距离是25mm.
【点睛】本题考查的是等边三角形的判定与性质,圆的性质,垂径定理的应用,勾股定理的应用,熟练垂径定理的运用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3垂径定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图、已知为的直径,点为的中点.则下列结论中一定正确的是( )
A. B. C. D.
2.将一张正方形的透明纸片ABCD和按如图位置叠放,顶点A、D在上,边AB、BC、CD分别与相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B.
C. D.
3.如图,“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”.用几何语言可表述为:为的直径,弦于点,寸,寸,则直径的长为( )
A.12.5寸 B.13寸 C.25寸 D.26寸
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( )
A.8 B.2 C.3 D.4
5.《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,为的直径,弦于,寸,寸,求直径的长.”则
A.寸 B.寸 C.寸 D.寸
6.如图,在⊙O中,半径OC⊥AB于点E,AE=2,则下列结论正确的是( )
A. B.
C.垂直平分 D.垂直平分
7.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
8.如图,⊙O的弦AB=8,P是劣弧AB中点,连接OP交AB于C,且PC=2,则⊙O的半径为( )
A.8 B.4 C.5 D.10
9.如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A.2 B.6 C.14 D.18
10.往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,则水的最大深度为( )
A. B. C. D.
11.如图,已知的半径为10,弦,则点到的距离是( )
A. B. C. D.
12.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )
A.1组 B.2组 C.3组 D.4组
二、填空题
13.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为 .
14.如图,以O为圆心的两个同心圆,过点的直径与外圆交于C,D两点,若CE=8,ED=2,则AB长 时,外圆的弦AB与内圆相切于点E.
15.如图,半圆O的直径AB=4cm,,点C是上的一个动点(不与点B,G重合),CD⊥OG于点D,CE⊥OB于点E,点E与点F关于点O中心对称,连接DE、DF,则△DEF面积的最大值为 cm2
16.已知的半径为2,弦,是上一点,且,直线与交于点,则的长为 .
17.如图,在△ABC中,∠ACB=90°,以C为圆心,CA长为半径的圆交AB于D,若AC=6,BC=8,则AD= .
三、解答题
18.如图,点P的坐标为(4,0),⊙P的半径为5,且⊙P与x轴交于点A、B,与y 轴交于点C、D,试求出点A、B、C、D的坐标.
19.点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.
20.如图是一个管道的横截面,圆心到水面的距离是3,水面宽.
(1)求这个管道横截面的半径.
(2)求的度数.
21.已知,⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC.
求证:AC2=AEAB.
22.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
23.如图,P是⊙O外一点,PA交⊙O于点B,PD交⊙O于点C,且∠APO=∠DPO. 弦AB与CD相等吗?为什么?
24.如图,在半径为的中,弦长.求:
(1)的度数;
(2)点O到的距离.
《3.3垂径定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D C D A C A B
题号 11 12
答案 B D
1.B
【分析】本题考查了垂径定理及其推论,根据垂径定理中“知二推三”进行推理论证,即可解题.
【详解】解:为的直径,点为的中点.
,
故选:B.
2.C
【分析】连接,根据弦与弧的关系,只要比较弦长即可比较弧长的大小即可求解.
【详解】如图,连接,过点作,交于,交于,则,
四边形是正方形,
,,
,
四边形是矩形,
,
,
,
,
,
A. ,,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. ,,故该选项正确,符合题意;
D.,,故该选项不正确,不符合题意;
故选:C.
【点睛】本题考查了弦与弧的关系,掌握同圆或等圆中,等弦对等弧是解题的关键.
3.D
【分析】连接,根据垂径定理,设直径为寸,利用列方程即可.
【详解】解:连接,
设直径的长为寸,则半径寸,
∵为⊙O的直径,弦于E,寸,
∴ ,
根据勾股定理得,
解得,
(寸).
故选:D.
【点睛】本题考查了垂径定理和勾股定理;熟练掌握垂径定理,由勾股定理得出方程是解决问题的关键.
4.D
【分析】如图,连接OD,利用勾股定理求出OE,再利用勾股定理求出AD即可.
【详解】解:如图,连接OD.
∵AB⊥CD,
∴CE=ED=4,
∵∠OED=90°,OD=5,
∴OE===3,
∴AE=OA+OE=8,
∴AD===4,
故选:D.
【点睛】本题考查垂径定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.C
【分析】连接AO,根据垂径定理及勾股定理即可求出半径,即可求出CD的长.
【详解】如图,连接AO,设AO=OD=r,
故OE=r-1,
∵AB=10,∴AE=5,
由AO2=AE2+OE2,即r2=52+( r-1)2,
解得r=13,故CD=2r=26
故选C
【点睛】此题主要考查垂径定理,解题的关键是根据勾股定理进行求解.
6.D
【分析】由垂径定理和勾股定理分别对各个选项进行判断即可.
【详解】解:连接OA,
条件不足,不能求出OE和EC的长,故选项A、B不符合题意;
∵OC⊥AB于点E,
∴OC是线段AB的垂直平分线,故选项D正确,符合题意;
选项C不符合题意,
故选:D.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
7.A
【分析】由题意可知,C、O、G三点在一条直线上OG最小,MN最大,再由勾股定理求得AB,然后由三角形面积求得CF,最后由垂径定理和勾股定理即可求得MN的最大值.
【详解】解:如图,过O作OG⊥AB于G,连接OC、OM,
∵DE=6,∠ACB=90°,OD=OE,
∴OC=DE=3,
∵OM=3,
∴只有OG最小,GM才能最大,从而MN有最大值,
∴只有C、O、G三点在一条直线上OG最小,
过C作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10,
∵AC BC=AB CF,
∴CF=,
∴OG=CF OC=,
∴MG==,
∴MN=2MG=
故选:A
【点睛】本题考查了勾股定理,垂线段最短,垂径定理等知识,正确作出辅助线,得出C、O、G三点在一条直线上OG最小是解题的关键.
8.C
【详解】解:连接OA,
∵P是劣弧AB中点,
∴OP⊥AB,AC=AB=×8=4,
设⊙O的半径为x,
则OC=OP﹣PC=x﹣2,
在Rt△OAC中,
OA2=OC2+AC2,
∴x2=42+(x﹣2)2,
解得:x=5,
∴⊙O的半径为5.
故选C.
9.A
【分析】要满足最短弦,只需满足垂直于该弦,再用垂径定理和勾股定理求得最短弦,由过点D的所有弦中,最长弦是直径,即可得到答案.
【详解】解:根据题意可知,要满足最短弦,只需满足垂直于该弦,设该最短弦是,如图,于点D,
∴,,
∴,
∴,
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为,
故选:A
【点睛】此题考查了垂径定理、勾股定理等知识,熟练掌握过圆内一点的最长弦和最短弦是解题的关键.
10.B
【分析】连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出CD的长.
【详解】解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,
∵OC⊥AB,由垂径定理可知,
∴AC=CB=AB=12,
在Rt△AOC中,由勾股定理可知:
∴,
∴,
故选:B.
【点睛】本题考查了垂径定理及勾股定理的应用,属于基础题,关键是过O点作AB的垂线,由此即可求解.
11.B
【分析】过点作于点,由垂径定理可得,然后在中由勾股定理即可求出点到的距离.
【详解】解:过点作于点,如下图,
∵,,
∴,
∵的半径为10,即,
∴在中,,
即点到的距离是8.
故选:B.
【点睛】本题主要考查了垂径定理以及勾股定理的应用,理解并掌握垂径定理是解题关键.
12.D
【分析】先根据OH⊥AB于点H可知,AH=BH,CH=DH,故可得出AC=BD,AD=BC,进而可得出结论.
【详解】解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC=BD.
所以共有4组相等的线段.
故选:D.
【点睛】本题考查的是垂径定理,熟知垂直于弦的直径平分弦是解答此题的关键.
13.(6,0)
【详解】解:过点P作PM⊥AB于M,则M的坐标是(4,0)
∴MB=MA=4-2=2,
∴点B的坐标为(6,0)
14.8
【分析】连接OA,首先求得半径的长,则OE即可求解,然后在直角△OAE中,利用勾股定理即可求得AE的长,则AB即可求解.
【详解】连接OA,则圆的半径OA=,
则OE=5-2=3,
在直角△OAE中,AE=,
∴AB=2AE=8.
【点睛】本题考查了切线的性质以及垂径定理,正确求得AE的长是关键.
15.2
【分析】连接OC,设OD=x,OE=OF=y.根据S△DEF=×EF×OD=×2y×x=xy,当xy的值最大时,△DEF的面积最大;根据矩形的性质,通过判定四边形ODCE是矩形,得;根据勾股定理、完全平方公式的性质分析,可得结论.
【详解】连接OC,设OD=x,OE=OF=y.
∵
∴OG⊥AB,
∵S△DEF=×EF×OD=×2y×x=xy,
∴xy的值最大时,△DEF的面积最大,
∵CD⊥OG于点D,CE⊥OB于点E,
∴∠CEO=∠CDO=∠DOE=90°,
∴四边形ODCE是矩形,
∴
∴x2+y2=22,即x2+y2=4,
∵(x﹣y)2≥0,
∴x2+y2≥2xy,
∴2xy≤4,
∴xy≤2,
∴xy的最大值为2,
∴△DEF的面积的最大值为2 cm2
故答案为:2.
【点睛】本题考查了圆、勾股定理、中心对称、矩形、完全平方公式的知识;解题的关键是熟练掌握圆的对称性、勾股定理、完全平方公式的性质,从而完成求解.
16.1或3
【分析】根据垂径定理建立直角三角形,再运用勾股定理求得,进而分两种情况讨论即可.
【详解】如图,连接,
,由垂径定理可知,,,
则在中,,
或,
故答案为:1或3.
【点睛】本题考查了垂径定理,勾股定理计算圆周上点到弦得距离,熟练掌握基本定理,准确分类讨论是解题关键.
17.7.2.
【分析】作CE⊥AB于E,根据勾股定理求出AB,根据三角形的面积公式求出CE,根据勾股定理求出AE,根据垂径定理计算.
【详解】解:作CE⊥AB于E,
△ABC中,∠ACB=90°,
∴AB===10,
△ABC的面积=×AC×BC=×AB×CE,
∴6×8=10×CE,
解得,CE=4.8,
由勾股定理得,AE===3.6,
∵CE⊥AB,
∴AD=2AE=7.2.
故答案为:7.2.
【点睛】本题考查垂径定理,勾股定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
18.A(-1,10),B(9,0),C(0,3),D(0,-3)
【分析】先根据点P的坐标为(3,0),⊙P的半径为5结合勾股定理可得点C、点D的坐标,再根据⊙P的半径为5可得AO、PB的长,即可求得点A、点B的坐标.
【详解】解:∵点P的坐标为(3,0),⊙P的半径为5
∴OP=3,CO=DO=4
∴点C的坐标为(4,0),点D的坐标为(-4,0)
∵⊙P的半径为5
∴AO=2,PB=5
∴点A的坐标为(-2,0),OB=8
∴点B的坐标为(8,0).
【点睛】本题考查了勾股定理,垂径定理以及点的坐标,本题知识点多,综合性强,在中考中比较常见,在各种题型中均有出现,一般难度不大,需熟练掌握.
19.289或119
【分析】要求梯形的面积就要先求出梯形的高,然后利用梯形的面积公式计算;求梯形的高,先利用垂径定理和勾股定理求出圆心到梯形两底的距离,进而得到梯形的高,由此结合梯形的面积公式即可得到其面积.
【详解】
解:连接OA、OD,作OE⊥AB,OF⊥CD,垂足分别为E、F,在Rt△AOE中,OA=13,AE=12,OE==5;同理可得OF=12
分两种情况:如图1.EF=OF+OE=12+5=17
如图2.EF=OF-OE=12-5=7
因此梯形的面积为(AB+CD)EF=(24+10)EF=289或119.
故答案为289或119.
【点睛】本题考查面积计算,勾股定理,垂径定理及推论,注意本题需分情况求解梯形的面积,即分圆心在梯形的内部与外部两种情况求解.
20.(1)
(2)
【分析】(1)根据垂径定理,可知是等腰直角三角形,再根据勾股定理即可解;
(2)根据等腰直角三角形的性质即可得出答案.
【详解】(1)解:如图,连接,
是等腰直角三角形,
在中,
这个管道横截面的半径为.
(2)解:在等腰直角中,,
在等腰直角中,,
.
【点睛】本题考查了垂径定理、勾股定理、等腰直角三角形的性质,解题关键是熟练掌握垂径定理和勾股定理.
21.见解析
【分析】连接BC,根据垂径定理得到BC=AC,根据等边对等角得到∠CAB=∠CBA,∠CAB=∠ECA,证明△AEC∽△ACB,根据相似三角形的性质得到即可证明.
【详解】连接BC,
∵AB⊥CD,CD为⊙O的直径
∴BC=AC,
∴∠CAB=∠CBA
又EA=EC,
∴∠CAB=∠ECA
∴∠CBA=∠ECA
∴△AEC∽△ACB
即AC2=AEAB.
【点睛】考查垂径定理,等腰三角形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题的关键.
22.居民楼会受到噪声的影响,17.3s
【分析】过点A作AB⊥MN,利用锐角三角函数的定义求出AB的长与200m相比较即可;过点A作AD=OA=200m,求出OD的长即可得出居民楼受噪音影响的时间.
【详解】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3 s.
【点睛】本题是解直角三角形的应用,主要考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
23.AB=CD.
【分析】过O点分别作AB和CD的垂线,交点分别为E和F,连接AO和DO.由垂径定理可得OE和OF分别是AB和CD的垂直平分线;证明△PEO≌△PFO得OE=OF,再证△AEO≌△DFO得AE=DF即可.
【详解】解:AB=CD.
证明:过O点分别作AB和CD的垂线,交点分别为E和F,连接AO和DO,
∵∠OEP=∠OFP=90°,∠APO=∠DPO,PO=PO,
∴△PEO≌△PFO,
∴OE=OF,
∵OE为弦AB的垂线,OF为弦CD的垂线,
∴AE=EB,DF=CF,、
∵AO=DO,
∴△AEO≌△DFO,
∴AE=DF,
∴AB=2AE=2DF=CD,
即AB=CD.
【点睛】本题结合三角形全等综合考察了垂径定理的知识.
24.(1)60°;(2)25mm
【分析】(1)证明是等边三角形,从而可得结论;
(2)过点O作OC⊥AB,垂足为点C,利用垂径定理求解 再利用勾股定理可得答案.
【详解】解:(1)∵OA,OB是⊙O的半径,
∴OA=OB=50mm,
又∵AB=50mm,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=60°.
(2)过点O作OC⊥AB,垂足为点C,如图所示,
由垂径定理得AC=CB=AB=25mm,
在Rt△OAC中OC2=OA2-AC2=502-252=252×3,
∴OC==25(mm),
即点O到AB的距离是25mm.
【点睛】本题考查的是等边三角形的判定与性质,圆的性质,垂径定理的应用,勾股定理的应用,熟练垂径定理的运用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
