6.3三角形的中位线同步强化练习(含解析)
文档属性
| 名称 | 6.3三角形的中位线同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 21:58:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
6.3三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,点D是上一动点,作且,连接分别是的中点,连接,则长为( )
A.6 B. C. D.
2.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.已知△ABC的各边长度分别为3cm,4cm,5cm,则连接各边中点的三角形的周长为( )
A.2cm B.7cm C.5cm D.6cm
4.如图,在中,,,、是的中位线,则四边形的周长是( )
A.5 B.7 C.8 D.10
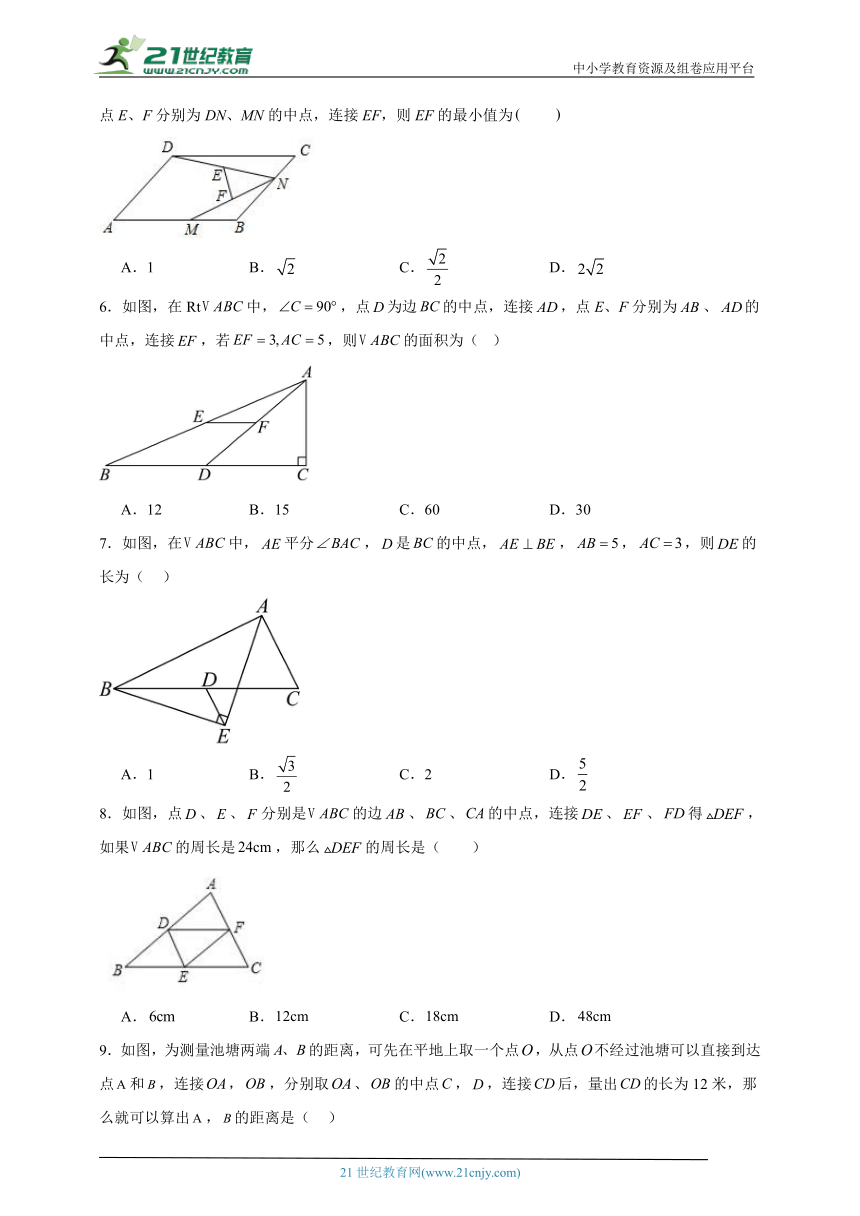
5.如图,在 ABCD中,,,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为
A.1 B. C. D.
6.如图,在Rt中,,点为边的中点,连接,点E、F分别为、的中点,连接,若,则的面积为( )
A.12 B.15 C.60 D.30
7.如图,在中,平分,是的中点,,,,则的长为( )
A.1 B. C.2 D.
8.如图,点、、分别是的边、、的中点,连接、、得,如果的周长是,那么的周长是( )
A. B. C. D.
9.如图,为测量池塘两端的距离,可先在平地上取一个点,从点不经过池塘可以直接到达点和,连接,,分别取、的中点,,连接后,量出的长为12米,那么就可以算出,的距离是( )
A.36米 B.24米 C.12米 D.6米
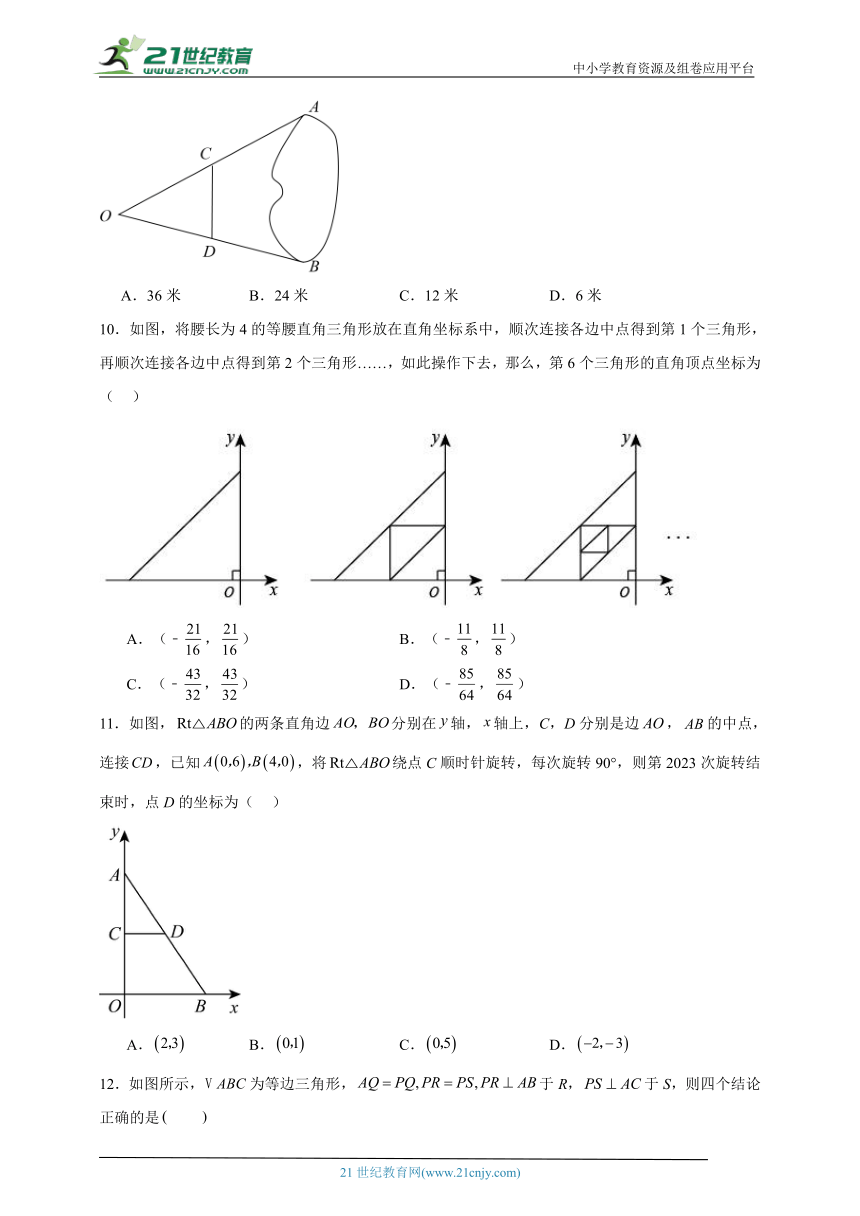
10.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )
A.(﹣,) B.(﹣,)
C.(﹣,) D.(﹣,)
11.如图,的两条直角边分别在轴,轴上,C,D分别是边,的中点,连接,已知,将绕点C顺时针旋转,每次旋转90°,则第2023次旋转结束时,点D的坐标为( )
A. B. C. D.
12.如图所示,为等边三角形,于R,于S,则四个结论正确的是
点P在的平分线上;
②;
③;
.
A.全部正确 B.仅和正确 C.仅正确 D.仅和正确
二、填空题
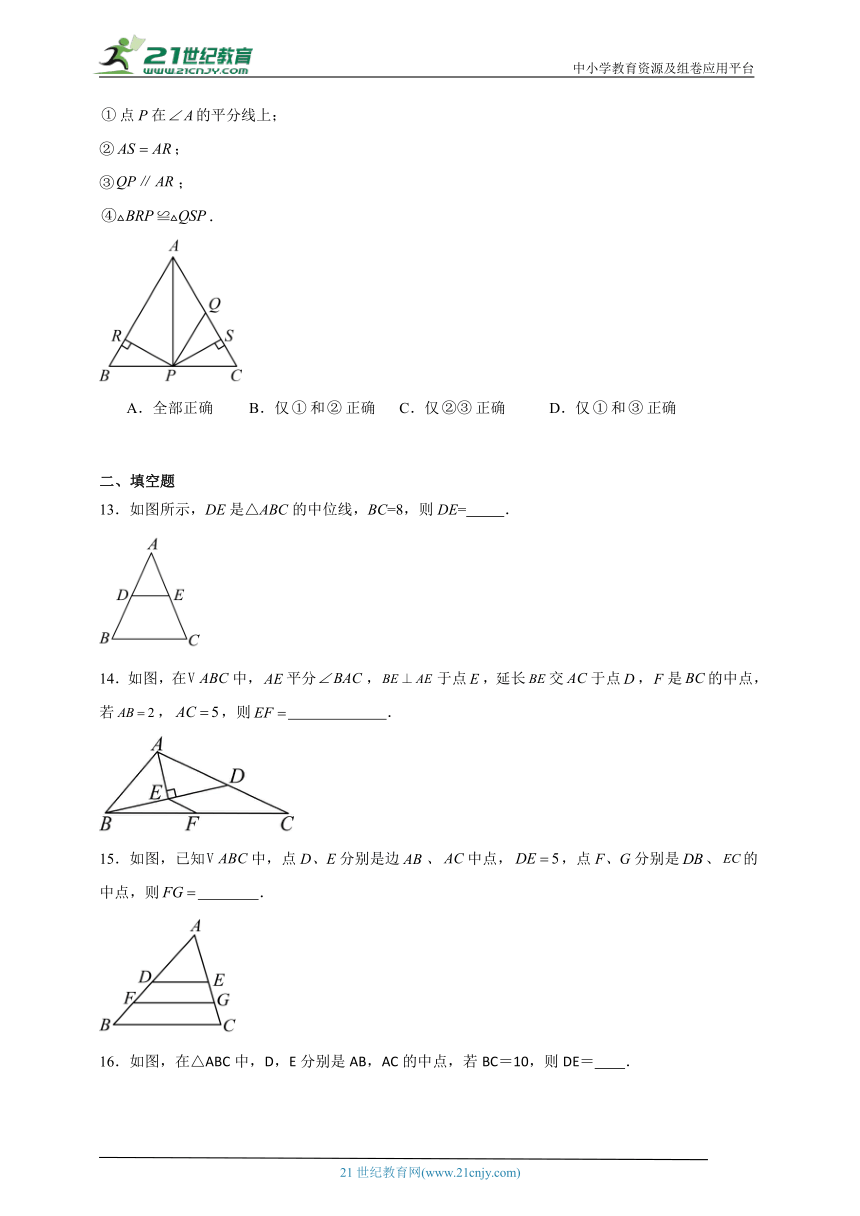
13.如图所示,DE是△ABC的中位线,BC=8,则DE= .
14.如图,在中,平分,于点,延长交于点,是的中点,若,,则 .
15.如图,已知中,点D、E分别是边、中点,,点F、G分别是、的中点,则 .
16.如图,在△ABC中,D,E分别是AB,AC的中点,若BC=10,则DE= .
17.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠FPE的度数是 .
三、解答题
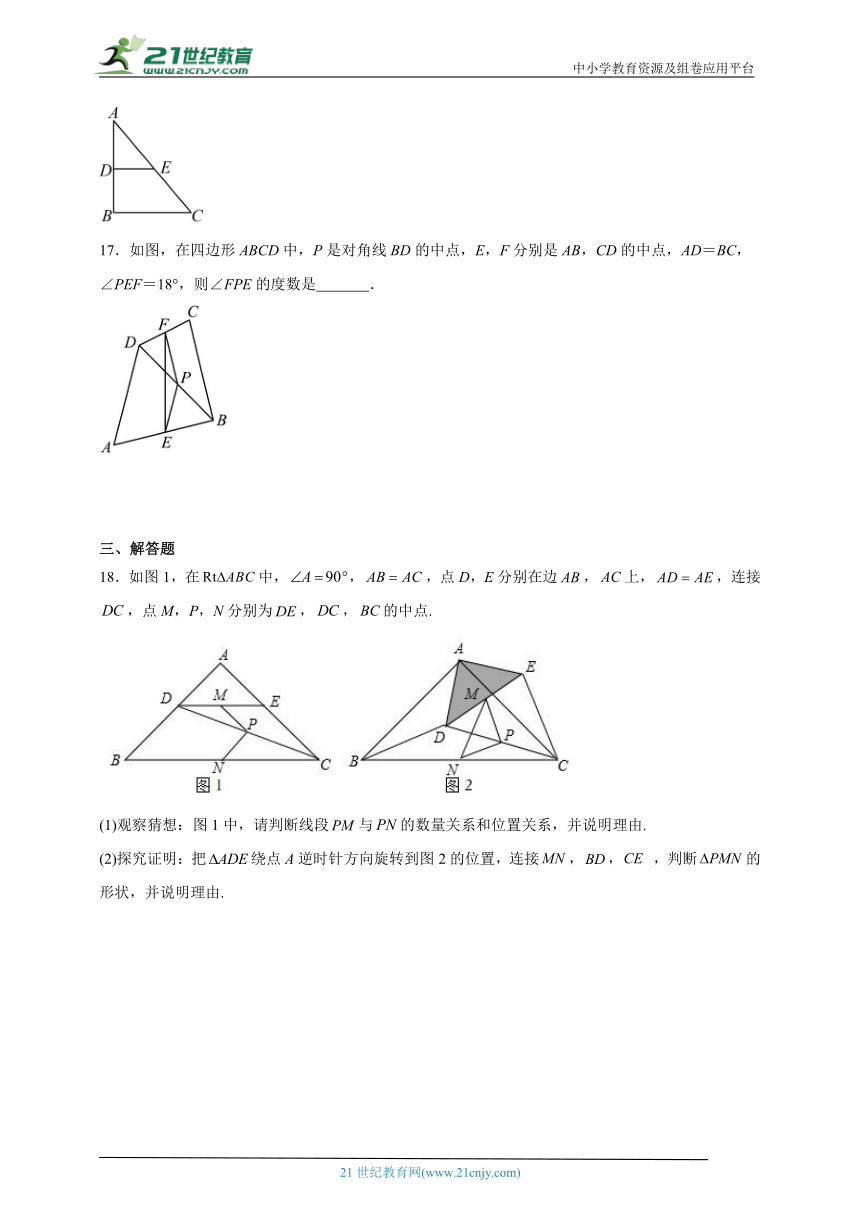
18.如图1,在中,,,点D,E分别在边,上,,连接,点M,P,N分别为,,的中点.
(1)观察猜想:图1中,请判断线段与的数量关系和位置关系,并说明理由.
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,, ,判断的形状,并说明理由.
19.如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出的中点M,N,并测出的长,如果M,N两点之间还有阻隔,你有什么解决办法?说明你的理由.
20.(1)回归课本
请用文字语言表述三角形的中位线定理:________________.
(2)回顾证法
证明三角形中位线定理的方法很多,但多数都要通过添加辅助线构图完成.下面是其中一种辅助线的添加方法.请结合图2,补全求证及证明过程.
已知:在中,点分别是的中点.
求证:________________.
证明:过点作,与的延长线交于点.
(3)实践应用
如图3,点和点被池塘隔开,在外选一点,连接,分别取的中点,测得的长度为9米,则两点间的距离为________________.
21.如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形中,最多可以有几个平行四边形,证明你的结论.
22.如图所示,点E,F,G,H分别是四边形的边的中点,求证:四边形是平行四边形.
23.如图,在梯形ABCD中,AD∥BC,E是DC的中点,EF∥AB交BC于F,若EF=4,求AB的长.
24.如图,△ABC的中线BE,CF相交于点G,已知P,Q分别是BG,CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请判断BG与GE的数量关系,并证明.
《6.3三角形的中位线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D B D A B B A
题号 11 12
答案 C A
1.C
【分析】本题考查了三角形中位线定理、勾股定理、平行线的性质;熟练掌握勾股定理,由三角形中位线定理得出是解题的关键.
由勾股定理得出,取中点,连接,证出是的中位线,是的中位线,由三角形中位线定理得出,证出,再由勾股定理求出即可.
【详解】解:∵,
,
取中点,连接,如图所示:
∵分别是的中点,
∴是的中位线,是的中位线,
∴,
∵,
∴,
∴;
故选:C.
2.B
【分析】根据直角三角形的斜边的中线等于斜边的一半,得到DF=5,由三角形中位线的性质得到DE=8,最后由线段的和差解题即可.
【详解】解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
故选:B.
【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.
3.D
【详解】如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=6cm,
故选D.
4.D
【分析】本题考查三角形中位线的性质,根据三角形中位线的性质可得四边形的各边长,进而即可求出周长.
【详解】解:∵、是的中位线,
∴,,
,,
∴.
故选:D
5.B
【分析】由已知可得,EF是三角形DMN的中位线,所以,当DM⊥AB时,DM最短,此时EF最小.
【详解】连接DM,
因为,E、F分别为DN、MN的中点,
所以,EF是三角形DMN的中位线,
所以,EF=,
当DM⊥AB时,DM最短,此时EF最小.
因为,,
所以,DM=AM,
所以,由勾股定理可得AM=2,此时 EF==.
故选B
【点睛】本题考核知识点:三角形中位线,平行四边形,勾股定理.解题关键点:巧用垂线段最短性质.
6.D
【分析】本题考查了三角形中位线的性质,中点性质,由三角形中位线的性质可得,又由中点性质可得,再根据三角形的面积公式即可求解,掌握三角形中位线的性质是解题的关键.
【详解】解:∵点分别为的中点,
∴为的中位线,
∴,
∵点为边的中点,
∴,
∵,,
∴,
故选:D.
7.A
【分析】本题考查了等腰三角形的判定与性质,三角形中位线的性质定理,关键是作辅助线得到等腰三角形.
延长交的延长线于点,证明是等腰三角形,则得的长,点E是的中点,求得的长,从而是中位线,即可求得的长.
【详解】延长交的延长线于点,如图,
,
,
平分,
,
,
是等腰三角形,
,点E是的中点,
,是的中位线,
.
故选:A.
8.B
【分析】由于D、E分别是AB、BC的中点,则DE是△ABC的中位线,那么DE=AC,同理有EF=AB,DF=BC,于是易求△DEF的周长.
【详解】、分别是的边、的中点,
,
同理,,,
.
故选B.
【点睛】本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.
9.B
【分析】根据题意可知为三角形的中位线,结合三角形中位线的性质即可获得答案.
【详解】解:如下图,连接,
∵、分别为、的中点,
∴为的中位线,
又∵米,
∴米.
故选:B.
【点睛】本题主要考查了三角形中位线的应用,理解并掌握三角形中位线的性质是解题关键.
10.A
【分析】利用等腰直角三角形的性质及三角形中位线的性质分别求出第1个到第6个三角形的直角顶点坐标即可.
【详解】由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣);
第4个三角形的直角顶点坐标:(﹣);
第5个三角形的直角顶点坐标:(﹣);
第6个三角形的直角顶点坐标:(﹣);
故选A.
【点睛】本题考查了三角形的中位线定理、等腰直角三角形的性质、中点三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
11.C
【分析】根据已知条件求出点D的坐标,探究规律,利用规律解决问题即可.
【详解】∵
∴
∵C,D分别是边,的中点,
∴,,
∴点D的坐标为,点C的坐标为
∴第1次旋转结束时,点D在C点正下方,且,点D的坐标为,
第2次旋转结束时,点D在C点左边,且,,点D的坐标为,
第3次旋转结束时,点D在C点正上方,且,点D的坐标为,
则第4次旋转结束时,点D的坐标为,
观察可知,4次一个循环,
∵,
∴第2023次旋转结束时,点D的坐标为,
故选:C.
【点睛】本题考查了坐标与图形变化-旋转、规律型-点的坐标,解决本题的关键是根据旋转的性质发现规律,总结规律.
12.A
【分析】因为为等边三角形,根据已知条件可推出,则,故(2)正确,,所以是等边三角形的顶角的平分线,故(1)正确,根据等腰三角形的三线合一的性质知,也是边上的高和中线,即点P是的中点,因为,所以点Q是的中点,所以是边对的中位线,有,故(3)正确,又可推出,故(4)正确.
【详解】∵于R,于S
∴
∵
∴
∴,故(2)正确,
∴是等边三角形的顶角的平分线,故(1)正确;
∴是边上的高和中线,即点P是的中点,
∵,
∴点Q是的中点,
∴是边对的中位线,
∴,故(3)正确;
∵
∴,故(4)正确;
∴全部正确.
故选A.
【点睛】本题利用了等边三角形的性质:三线合一,全等三角形的判定和性质,中位线的性质求解.
13.4
【详解】根据三角形的中位线定理,得:DE=BC=4
故答案为4.
14.
【分析】根据角平分线的定义结合题意,即可利用“”证明,即得出,,从而可得出,点E为中点,从而可判定为的中位线,进而可求出的长.
【详解】∵平分,
∴,.
又∵,
∴,
∴,,
∴,点E为中点.
∵F是的中点,
∴EF为的中位线,
∴.
故答案为:.
【点睛】本题考查角平分线的定义,三角形全等的判定和性质,三角形中位线的性质等知识.掌握三角形的中位线平行于三角形的第三边,并且等于第三边的一半是解题关键.
15.
【分析】本题考查了三角形的中位线及梯形的中位线,熟练掌握两个定理是解题的关键.根据三角形的中位线平行于第三边并且等于第三边的一半求出,再根据梯形的中位线平行于两底边并且等于两底和的一半求解即可.
【详解】解:点D、E分别是边、中点,
是的中位线,
,,
,
,
点F、G分别是、的中点,
是梯形的中位线,
,
故答案为:
16.5
【详解】试题分析:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴BC=2DE,∵BC=10,∴DE=5.故答案为5.
考点:三角形中位线定理.
17.144°
【分析】根据中位线定理,易证明△EPF是等腰三角形,根据等腰三角形的性质即可求解.
【详解】解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF= BC,PE= AD,
∵AD=BC,
∴PF=PE,
∵∠PEF=18°,
∴∠PEF=∠PFE=18°.
∠FPE=180°-18°-18°=144°.
故答案为:144°.
【点睛】本题考查了三角形中位线定理及等腰三角形的性质,解题关键是利用中位线性质证明△EPF是等腰三角形.
18.(1),,理由见解析;
(2)是等腰直角三角形,理由见解析
【分析】(1)利用三角形的中位线得出,,进而判断出,即可得出结论,再利用三角形的中位线得出,得出,最后用互余即可得出结论;
(2)先判断出,得出,同(1)的方法得出,,即可得出,同(1)的方法即可得出结论.
【详解】(1)解:,理由如下:
∵点P,N是,的中点,
∴,,,
∵点P,M是,的中点,
∴,,,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:是等腰直角三角形,
理由如下:由旋转知,,
在和中,
,
∴,,
∴,,
利用三角形的中位线得,,,,
∴,
∴是等腰三角形,
同(1)的方法得, ,
∴,
同(1)的方法得,,
∴,
∵,
∴
,
∵,
∴,
∴,
∴是等腰直角三角形.
【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定和性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
19.用步测出CM,CN中点D、E, 只要测量出DE长,解答见详解.
【分析】用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,利用中位线性质可得DE=,MN=,可得AB=2MN=4DE即可.
【详解】解:用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,
∵点D、E分别为CM,CN的中点,
∴DE=(三角形的中位线平行于第三边,并且等于第三边的一半),
又∵点M,N分别为的中点,
∴MN=(三角形的中位线平行于第三边,并且等于第三边的一半),
∴AB=2MN=4DE.
∴只要测量出DE长便可求AB.
【点睛】本题考查三角形中位线性质在生活中运用,掌握三角形中位线性质是解题关键.
20.(1)三角形的中位线平行于三角形的第三边,并且等于第三边的一半;(2),;详见解析;(3)18米
【分析】(1)根据三角形的中位线定理直接阐述即可;
(2)过点作,与的延长线交于点,证明,再证四边形是平行四边形,即可证明结论;
(3)直接利用三角形中位线定理求解即可.
【详解】解:(1)三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
故答案为:三角形的中位线平行于三角形的第三边,并且等于第三边的一半;
(2)求证:,.
证明:∵点分别是的中点,
∴,,
过点作,与的延长线交于点.
∴,
在和中,
.
,.
,.
四边形是平行四边形,
,,
又,
,.
故答案为:,;
(3)∵点分别是的中点,米,
∴,即:米
故答案为:18米.
【点睛】本题考查了三角形中位线定理,平行四边形的判定和性质,解题的关键是理解题意,学会添加常用辅助线,构造特殊四边形解决问题.
21.3个,证明见解析.
【详解】试题分析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,利用三角形中位线定理分别进行证明即可得.
试题解析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,证明如下:
在四边形ABCD中F,G,H,E,M,N分别是AB,BC,CD,DA,BD,AC的中点,
∴FG∥AC,EH∥AC;FG=AC,EH=AC,
∴FG∥EH,FG=EH,
∴四边形FGHE是平行四边形,
MG∥CD,EN∥CD;MG=CD,EN=CD,
∴MG∥EN,MG=EN ,
∴四边形MGNE是平行四边形,
FM∥AD,NH∥AD;FM=AD,NH=AD,
∴FM∥NH;FM=NH,
∴四边形FMHN是平行四边形,
∴最多可以有3个平行四边形.
22.见解析
【分析】连接BD,利用三角形的中位线定理证明得出,从而得到四边形是平行四边形
【详解】解:如图,连接.
∵点E,H分别是线段的中点,
∴是的中位线,
∴EH∥BD,.
同理,.
∴,
∴四边形是平行四边形.
【点睛】此题主要考查了三角形中位线定理和平行四边形的判定方法,题目比较典型,又有综合性,难度不大,解题的关键是正确的添加辅助线,把四边形的问题转化为三角形的问题.
23.8
【详解】试题分析:过D作DG∥AB交BC于G,则可得四边形ABGD是平行四边形,从而有AB=DG,
又由已知可知EF是△CDG的中位线,利用三角形中位线性质定理可得DG=2EF,从而问题得解.
试题解析:过D作DG∥AB交BC于G,∵AD∥BC,AB∥DG,
∴四边形ABGD是平行四边形,∴AB=DG,
∵EF∥AB,∴EF∥DG,∵DE=CE,∴GF=CF,
∴EF是△CDG的中位线,∴EF=DG,
∴DG=2EF=8,即AB=8.
24.(1)证明见解析;(2)BG=2GE.
【详解】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是BG的中点可得BG=2PG,利用等量代换可得答案.
试题解析:(1)∵BE、CF是△ABC的中线,∴EF是△ABC的中位线,
∴EF∥BC且EF=BC,
∵P、Q分别是BG、CG的中点,∴PQ是△BCG的中位线,
∴PQ∥BC且PQ=BC,
∴EF∥PQ且EF=PQ,
∴四边形EFPQ是平行四边形;
(2)BG=2GE,
∵四边形EFPQ是平行四边形,∴GP=GE,
∵P是BG中点,∴BG=2PG,
∴BG=2GE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在中,,点D是上一动点,作且,连接分别是的中点,连接,则长为( )
A.6 B. C. D.
2.如图,在ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.已知△ABC的各边长度分别为3cm,4cm,5cm,则连接各边中点的三角形的周长为( )
A.2cm B.7cm C.5cm D.6cm
4.如图,在中,,,、是的中位线,则四边形的周长是( )
A.5 B.7 C.8 D.10
5.如图,在 ABCD中,,,点M、N分别是边AB、BC上的动点,连接DN、MN,点E、F分别为DN、MN的中点,连接EF,则EF的最小值为
A.1 B. C. D.
6.如图,在Rt中,,点为边的中点,连接,点E、F分别为、的中点,连接,若,则的面积为( )
A.12 B.15 C.60 D.30
7.如图,在中,平分,是的中点,,,,则的长为( )
A.1 B. C.2 D.
8.如图,点、、分别是的边、、的中点,连接、、得,如果的周长是,那么的周长是( )
A. B. C. D.
9.如图,为测量池塘两端的距离,可先在平地上取一个点,从点不经过池塘可以直接到达点和,连接,,分别取、的中点,,连接后,量出的长为12米,那么就可以算出,的距离是( )
A.36米 B.24米 C.12米 D.6米
10.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )
A.(﹣,) B.(﹣,)
C.(﹣,) D.(﹣,)
11.如图,的两条直角边分别在轴,轴上,C,D分别是边,的中点,连接,已知,将绕点C顺时针旋转,每次旋转90°,则第2023次旋转结束时,点D的坐标为( )
A. B. C. D.
12.如图所示,为等边三角形,于R,于S,则四个结论正确的是
点P在的平分线上;
②;
③;
.
A.全部正确 B.仅和正确 C.仅正确 D.仅和正确
二、填空题
13.如图所示,DE是△ABC的中位线,BC=8,则DE= .
14.如图,在中,平分,于点,延长交于点,是的中点,若,,则 .
15.如图,已知中,点D、E分别是边、中点,,点F、G分别是、的中点,则 .
16.如图,在△ABC中,D,E分别是AB,AC的中点,若BC=10,则DE= .
17.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠FPE的度数是 .
三、解答题
18.如图1,在中,,,点D,E分别在边,上,,连接,点M,P,N分别为,,的中点.
(1)观察猜想:图1中,请判断线段与的数量关系和位置关系,并说明理由.
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,, ,判断的形状,并说明理由.
19.如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出的中点M,N,并测出的长,如果M,N两点之间还有阻隔,你有什么解决办法?说明你的理由.
20.(1)回归课本
请用文字语言表述三角形的中位线定理:________________.
(2)回顾证法
证明三角形中位线定理的方法很多,但多数都要通过添加辅助线构图完成.下面是其中一种辅助线的添加方法.请结合图2,补全求证及证明过程.
已知:在中,点分别是的中点.
求证:________________.
证明:过点作,与的延长线交于点.
(3)实践应用
如图3,点和点被池塘隔开,在外选一点,连接,分别取的中点,测得的长度为9米,则两点间的距离为________________.
21.如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形中,最多可以有几个平行四边形,证明你的结论.
22.如图所示,点E,F,G,H分别是四边形的边的中点,求证:四边形是平行四边形.
23.如图,在梯形ABCD中,AD∥BC,E是DC的中点,EF∥AB交BC于F,若EF=4,求AB的长.
24.如图,△ABC的中线BE,CF相交于点G,已知P,Q分别是BG,CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请判断BG与GE的数量关系,并证明.
《6.3三角形的中位线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D B D A B B A
题号 11 12
答案 C A
1.C
【分析】本题考查了三角形中位线定理、勾股定理、平行线的性质;熟练掌握勾股定理,由三角形中位线定理得出是解题的关键.
由勾股定理得出,取中点,连接,证出是的中位线,是的中位线,由三角形中位线定理得出,证出,再由勾股定理求出即可.
【详解】解:∵,
,
取中点,连接,如图所示:
∵分别是的中点,
∴是的中位线,是的中位线,
∴,
∵,
∴,
∴;
故选:C.
2.B
【分析】根据直角三角形的斜边的中线等于斜边的一半,得到DF=5,由三角形中位线的性质得到DE=8,最后由线段的和差解题即可.
【详解】解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=5,
∵BC= 16,D、E分别是AB,AC的中点,
∴DE=BC=8,
∴EF=DE-DF=3,
故选:B.
【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.
3.D
【详解】如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=6cm,
故选D.
4.D
【分析】本题考查三角形中位线的性质,根据三角形中位线的性质可得四边形的各边长,进而即可求出周长.
【详解】解:∵、是的中位线,
∴,,
,,
∴.
故选:D
5.B
【分析】由已知可得,EF是三角形DMN的中位线,所以,当DM⊥AB时,DM最短,此时EF最小.
【详解】连接DM,
因为,E、F分别为DN、MN的中点,
所以,EF是三角形DMN的中位线,
所以,EF=,
当DM⊥AB时,DM最短,此时EF最小.
因为,,
所以,DM=AM,
所以,由勾股定理可得AM=2,此时 EF==.
故选B
【点睛】本题考核知识点:三角形中位线,平行四边形,勾股定理.解题关键点:巧用垂线段最短性质.
6.D
【分析】本题考查了三角形中位线的性质,中点性质,由三角形中位线的性质可得,又由中点性质可得,再根据三角形的面积公式即可求解,掌握三角形中位线的性质是解题的关键.
【详解】解:∵点分别为的中点,
∴为的中位线,
∴,
∵点为边的中点,
∴,
∵,,
∴,
故选:D.
7.A
【分析】本题考查了等腰三角形的判定与性质,三角形中位线的性质定理,关键是作辅助线得到等腰三角形.
延长交的延长线于点,证明是等腰三角形,则得的长,点E是的中点,求得的长,从而是中位线,即可求得的长.
【详解】延长交的延长线于点,如图,
,
,
平分,
,
,
是等腰三角形,
,点E是的中点,
,是的中位线,
.
故选:A.
8.B
【分析】由于D、E分别是AB、BC的中点,则DE是△ABC的中位线,那么DE=AC,同理有EF=AB,DF=BC,于是易求△DEF的周长.
【详解】、分别是的边、的中点,
,
同理,,,
.
故选B.
【点睛】本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.
9.B
【分析】根据题意可知为三角形的中位线,结合三角形中位线的性质即可获得答案.
【详解】解:如下图,连接,
∵、分别为、的中点,
∴为的中位线,
又∵米,
∴米.
故选:B.
【点睛】本题主要考查了三角形中位线的应用,理解并掌握三角形中位线的性质是解题关键.
10.A
【分析】利用等腰直角三角形的性质及三角形中位线的性质分别求出第1个到第6个三角形的直角顶点坐标即可.
【详解】由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣);
第4个三角形的直角顶点坐标:(﹣);
第5个三角形的直角顶点坐标:(﹣);
第6个三角形的直角顶点坐标:(﹣);
故选A.
【点睛】本题考查了三角形的中位线定理、等腰直角三角形的性质、中点三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
11.C
【分析】根据已知条件求出点D的坐标,探究规律,利用规律解决问题即可.
【详解】∵
∴
∵C,D分别是边,的中点,
∴,,
∴点D的坐标为,点C的坐标为
∴第1次旋转结束时,点D在C点正下方,且,点D的坐标为,
第2次旋转结束时,点D在C点左边,且,,点D的坐标为,
第3次旋转结束时,点D在C点正上方,且,点D的坐标为,
则第4次旋转结束时,点D的坐标为,
观察可知,4次一个循环,
∵,
∴第2023次旋转结束时,点D的坐标为,
故选:C.
【点睛】本题考查了坐标与图形变化-旋转、规律型-点的坐标,解决本题的关键是根据旋转的性质发现规律,总结规律.
12.A
【分析】因为为等边三角形,根据已知条件可推出,则,故(2)正确,,所以是等边三角形的顶角的平分线,故(1)正确,根据等腰三角形的三线合一的性质知,也是边上的高和中线,即点P是的中点,因为,所以点Q是的中点,所以是边对的中位线,有,故(3)正确,又可推出,故(4)正确.
【详解】∵于R,于S
∴
∵
∴
∴,故(2)正确,
∴是等边三角形的顶角的平分线,故(1)正确;
∴是边上的高和中线,即点P是的中点,
∵,
∴点Q是的中点,
∴是边对的中位线,
∴,故(3)正确;
∵
∴,故(4)正确;
∴全部正确.
故选A.
【点睛】本题利用了等边三角形的性质:三线合一,全等三角形的判定和性质,中位线的性质求解.
13.4
【详解】根据三角形的中位线定理,得:DE=BC=4
故答案为4.
14.
【分析】根据角平分线的定义结合题意,即可利用“”证明,即得出,,从而可得出,点E为中点,从而可判定为的中位线,进而可求出的长.
【详解】∵平分,
∴,.
又∵,
∴,
∴,,
∴,点E为中点.
∵F是的中点,
∴EF为的中位线,
∴.
故答案为:.
【点睛】本题考查角平分线的定义,三角形全等的判定和性质,三角形中位线的性质等知识.掌握三角形的中位线平行于三角形的第三边,并且等于第三边的一半是解题关键.
15.
【分析】本题考查了三角形的中位线及梯形的中位线,熟练掌握两个定理是解题的关键.根据三角形的中位线平行于第三边并且等于第三边的一半求出,再根据梯形的中位线平行于两底边并且等于两底和的一半求解即可.
【详解】解:点D、E分别是边、中点,
是的中位线,
,,
,
,
点F、G分别是、的中点,
是梯形的中位线,
,
故答案为:
16.5
【详解】试题分析:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴BC=2DE,∵BC=10,∴DE=5.故答案为5.
考点:三角形中位线定理.
17.144°
【分析】根据中位线定理,易证明△EPF是等腰三角形,根据等腰三角形的性质即可求解.
【详解】解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF= BC,PE= AD,
∵AD=BC,
∴PF=PE,
∵∠PEF=18°,
∴∠PEF=∠PFE=18°.
∠FPE=180°-18°-18°=144°.
故答案为:144°.
【点睛】本题考查了三角形中位线定理及等腰三角形的性质,解题关键是利用中位线性质证明△EPF是等腰三角形.
18.(1),,理由见解析;
(2)是等腰直角三角形,理由见解析
【分析】(1)利用三角形的中位线得出,,进而判断出,即可得出结论,再利用三角形的中位线得出,得出,最后用互余即可得出结论;
(2)先判断出,得出,同(1)的方法得出,,即可得出,同(1)的方法即可得出结论.
【详解】(1)解:,理由如下:
∵点P,N是,的中点,
∴,,,
∵点P,M是,的中点,
∴,,,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:是等腰直角三角形,
理由如下:由旋转知,,
在和中,
,
∴,,
∴,,
利用三角形的中位线得,,,,
∴,
∴是等腰三角形,
同(1)的方法得, ,
∴,
同(1)的方法得,,
∴,
∵,
∴
,
∵,
∴,
∴,
∴是等腰直角三角形.
【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定和性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
19.用步测出CM,CN中点D、E, 只要测量出DE长,解答见详解.
【分析】用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,利用中位线性质可得DE=,MN=,可得AB=2MN=4DE即可.
【详解】解:用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,
∵点D、E分别为CM,CN的中点,
∴DE=(三角形的中位线平行于第三边,并且等于第三边的一半),
又∵点M,N分别为的中点,
∴MN=(三角形的中位线平行于第三边,并且等于第三边的一半),
∴AB=2MN=4DE.
∴只要测量出DE长便可求AB.
【点睛】本题考查三角形中位线性质在生活中运用,掌握三角形中位线性质是解题关键.
20.(1)三角形的中位线平行于三角形的第三边,并且等于第三边的一半;(2),;详见解析;(3)18米
【分析】(1)根据三角形的中位线定理直接阐述即可;
(2)过点作,与的延长线交于点,证明,再证四边形是平行四边形,即可证明结论;
(3)直接利用三角形中位线定理求解即可.
【详解】解:(1)三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
故答案为:三角形的中位线平行于三角形的第三边,并且等于第三边的一半;
(2)求证:,.
证明:∵点分别是的中点,
∴,,
过点作,与的延长线交于点.
∴,
在和中,
.
,.
,.
四边形是平行四边形,
,,
又,
,.
故答案为:,;
(3)∵点分别是的中点,米,
∴,即:米
故答案为:18米.
【点睛】本题考查了三角形中位线定理,平行四边形的判定和性质,解题的关键是理解题意,学会添加常用辅助线,构造特殊四边形解决问题.
21.3个,证明见解析.
【详解】试题分析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,利用三角形中位线定理分别进行证明即可得.
试题解析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,证明如下:
在四边形ABCD中F,G,H,E,M,N分别是AB,BC,CD,DA,BD,AC的中点,
∴FG∥AC,EH∥AC;FG=AC,EH=AC,
∴FG∥EH,FG=EH,
∴四边形FGHE是平行四边形,
MG∥CD,EN∥CD;MG=CD,EN=CD,
∴MG∥EN,MG=EN ,
∴四边形MGNE是平行四边形,
FM∥AD,NH∥AD;FM=AD,NH=AD,
∴FM∥NH;FM=NH,
∴四边形FMHN是平行四边形,
∴最多可以有3个平行四边形.
22.见解析
【分析】连接BD,利用三角形的中位线定理证明得出,从而得到四边形是平行四边形
【详解】解:如图,连接.
∵点E,H分别是线段的中点,
∴是的中位线,
∴EH∥BD,.
同理,.
∴,
∴四边形是平行四边形.
【点睛】此题主要考查了三角形中位线定理和平行四边形的判定方法,题目比较典型,又有综合性,难度不大,解题的关键是正确的添加辅助线,把四边形的问题转化为三角形的问题.
23.8
【详解】试题分析:过D作DG∥AB交BC于G,则可得四边形ABGD是平行四边形,从而有AB=DG,
又由已知可知EF是△CDG的中位线,利用三角形中位线性质定理可得DG=2EF,从而问题得解.
试题解析:过D作DG∥AB交BC于G,∵AD∥BC,AB∥DG,
∴四边形ABGD是平行四边形,∴AB=DG,
∵EF∥AB,∴EF∥DG,∵DE=CE,∴GF=CF,
∴EF是△CDG的中位线,∴EF=DG,
∴DG=2EF=8,即AB=8.
24.(1)证明见解析;(2)BG=2GE.
【详解】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是BG的中点可得BG=2PG,利用等量代换可得答案.
试题解析:(1)∵BE、CF是△ABC的中线,∴EF是△ABC的中位线,
∴EF∥BC且EF=BC,
∵P、Q分别是BG、CG的中点,∴PQ是△BCG的中位线,
∴PQ∥BC且PQ=BC,
∴EF∥PQ且EF=PQ,
∴四边形EFPQ是平行四边形;
(2)BG=2GE,
∵四边形EFPQ是平行四边形,∴GP=GE,
∵P是BG中点,∴BG=2PG,
∴BG=2GE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
