第三章图形的平移与旋转同步强化练习(含解析)
文档属性
| 名称 | 第三章图形的平移与旋转同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章图形的平移与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在RtABC中,BAC=,将ABC绕点A顺时针旋转后得到A(点B的对应点是点,点C的对应点是点),连接C.若C=,则B的大小是( )
A.32° B.64° C.77° D.87°
2.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )
A. B.
C. D.
3.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为( )
A. B. C. D.
4.将长方形绕着它的一边旋转一周得到的立体图形是( )
A.正方体 B.长方体 C.棱柱 D.圆柱
5.在下列生活现象中,不是平移的是( )
A.小亮荡秋千的运动 B.拉开抽屉的运动
C.站在运行的电梯上的人 D.坐在直线行驶的列车上的乘客
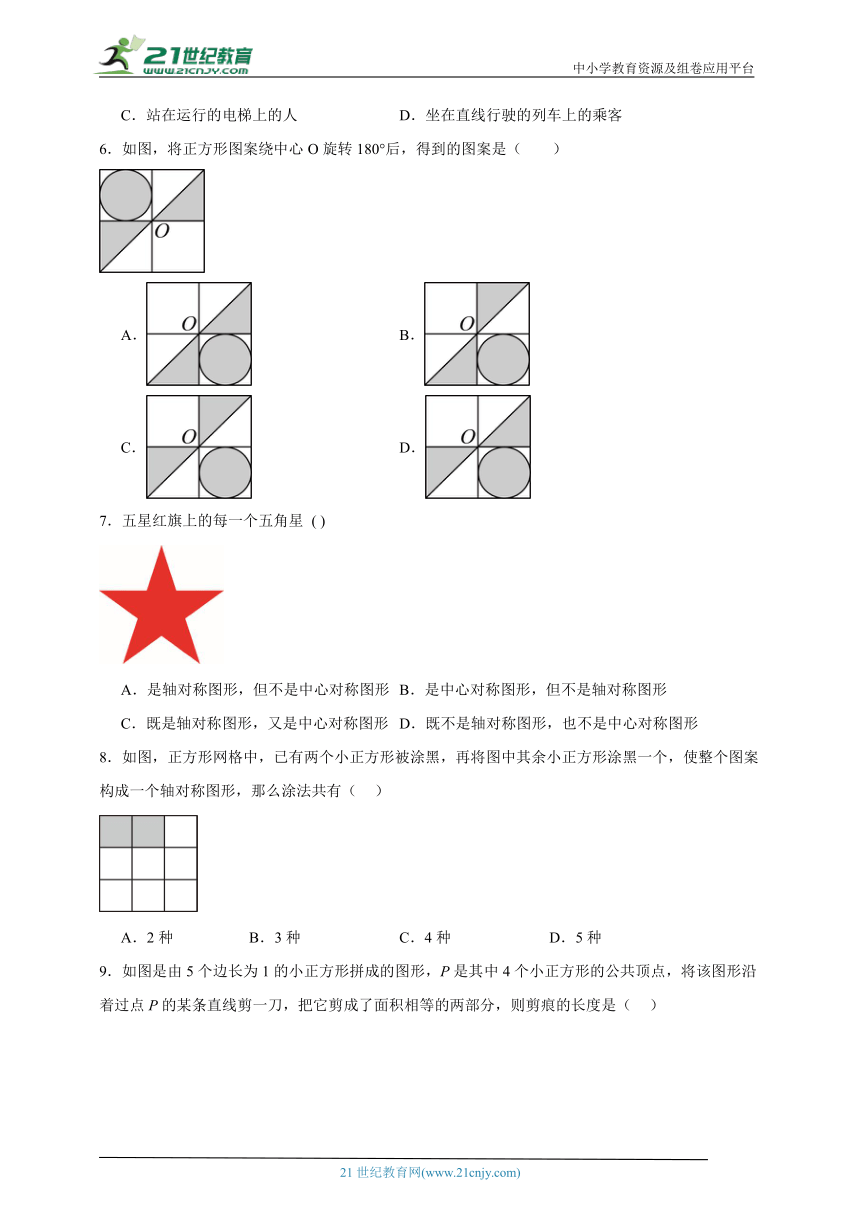
6.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
A. B.
C. D.
7.五星红旗上的每一个五角星 ( )
A.是轴对称图形,但不是中心对称图形 B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形 D.既不是轴对称图形,也不是中心对称图形
8.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.2种 B.3种 C.4种 D.5种
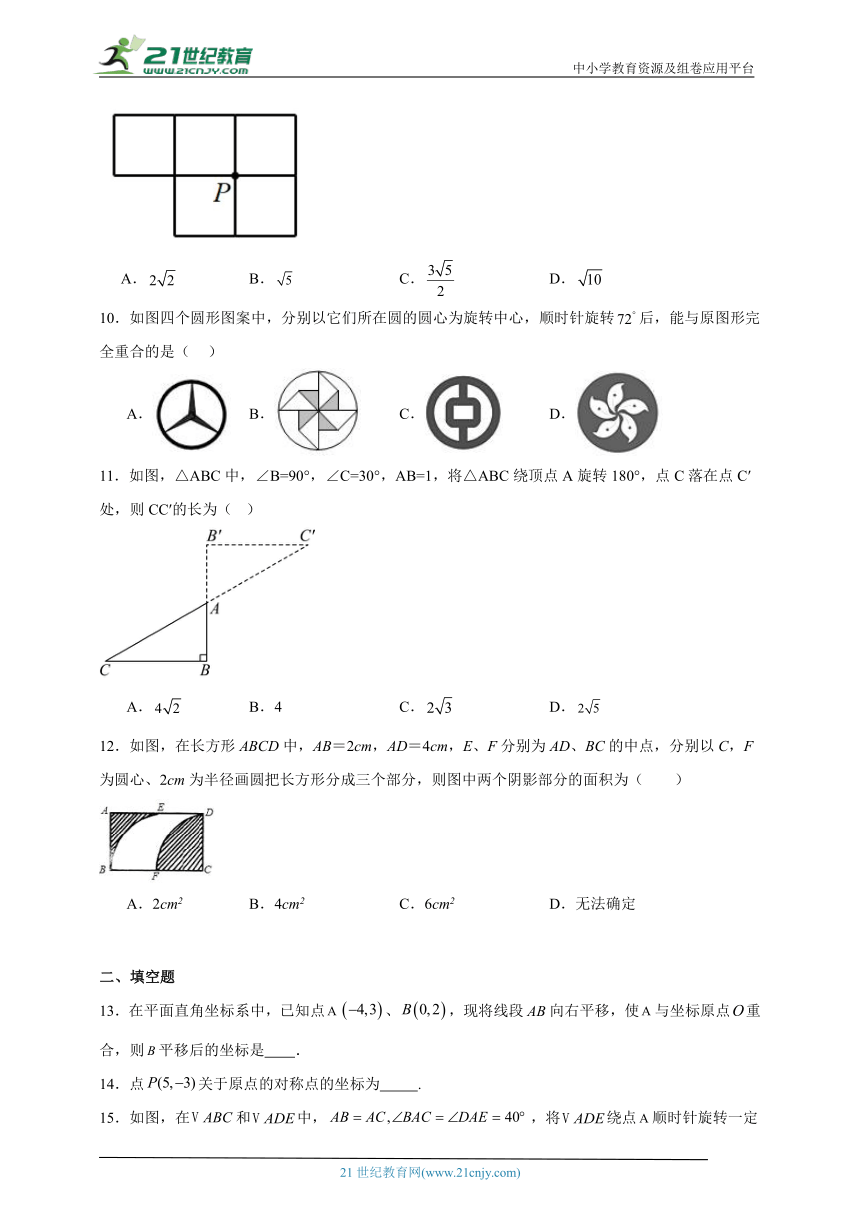
9.如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A. B. C. D.
10.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转后,能与原图形完全重合的是( )
A. B. C. D.
11.如图,△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C′处,则CC′的长为( )
A. B.4 C. D.
12.如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为( )
A.2cm2 B.4cm2 C.6cm2 D.无法确定
二、填空题
13.在平面直角坐标系中,已知点、,现将线段向右平移,使与坐标原点重合,则平移后的坐标是 .
14.点关于原点的对称点的坐标为 .
15.如图,在和中,,将绕点顺时针旋转一定角度,当时,的度数是 .
16.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为 m.
17.有五张分别印有圆、等腰三角形、矩形、菱形、正方形图案的卡片(卡片中除图案不同外,其余均相同),现将有图案的一面朝下任意摆放,从中任意抽取一张,抽到有中心对称图案的卡片的概率是 .
三、解答题
18.如图所示,△ABC平移后得到了△DEF,D在AB上,若∠A=26°,∠E=74°,求∠1,∠2,∠F,∠C的度数.
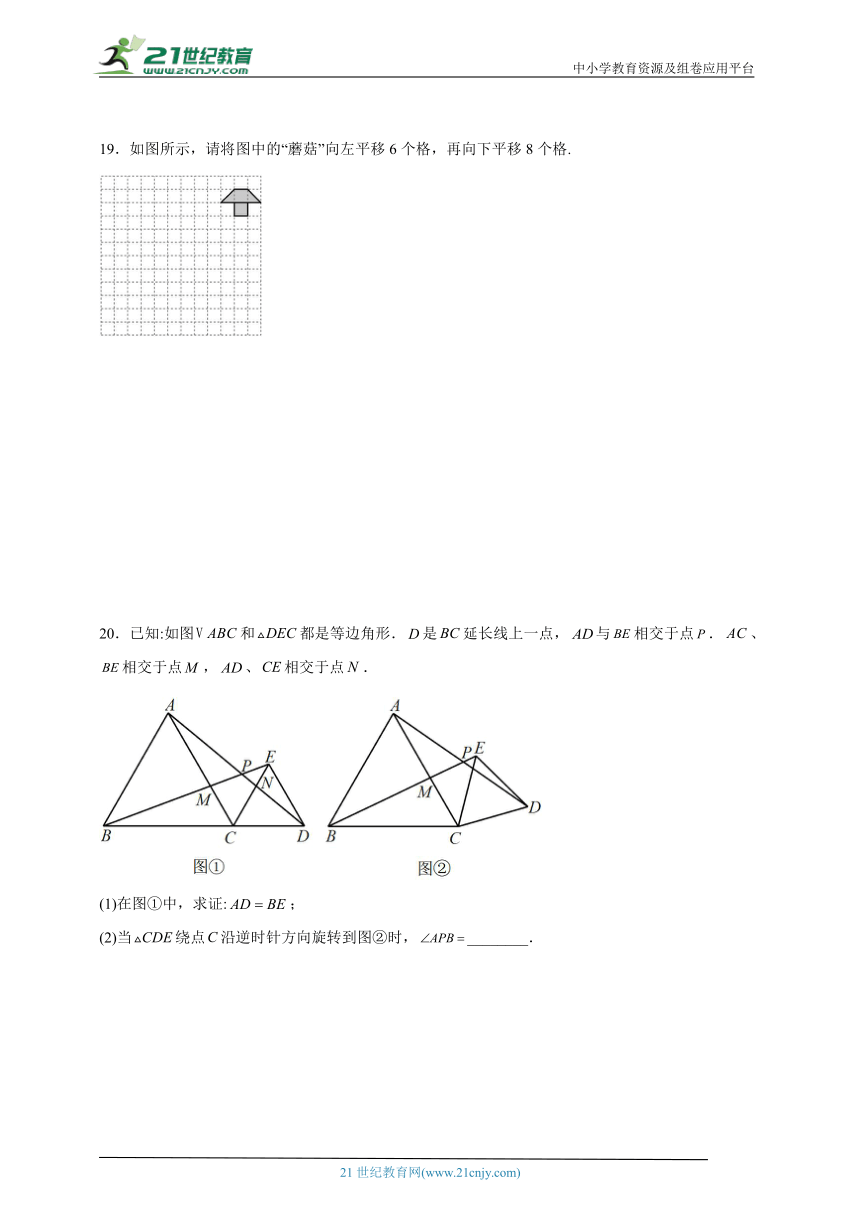
19.如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移8个格.
20.已知:如图和都是等边角形.是延长线上一点,与相交于点.、相交于点,、相交于点.
(1)在图①中,求证:;
(2)当绕点沿逆时针方向旋转到图②时,________.
21.如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
22.在如图的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上;
(1)建立适当的平面直角坐标系,使A(﹣2,﹣1),C(1,﹣1),写出B点坐标;
(2)在(1)的条件下,将△ABC向右平移4个单位再向上平移2个单位,在图中画出平移后的,并分别写出、、的坐标;
(3)求△ABC的面积.
(4)在y轴上是否存在点P,使得△ACP的面积和△ABC的面积相等,若存在,直接写出点P的坐标.
23.已知如图,正方形ABCD中,E为CD边上一点,F为BC边上一点,CE=CF.
(1)∠FDC=∠EBC,相等吗?
(2)△DCF能与△BCE重合吗?
(3)BE与DF垂直吗?
24.如图,在直角坐标系中,平行于x轴的线段上所有点的纵坐标都是,横坐标x的取值范围是,则线段上任意一点的坐标可以用“”表示.
按照类似这样的规定,回答下面的问题:
(1)怎样表示线段上任意一点的坐标?
(2)把线段向上平移2.5个单位,作出所得的线段.线段上任意一点的坐标怎样表示?
(3)把线段向左平移3个单位,作出所得的线段.线段上任意一点的坐标怎样表示?
《第三章图形的平移与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D A D A A D D
题号 11 12
答案 B B
1.C
【详解】解:根据旋转可得:,
则,
则 ,
则,
则根据旋转图形的性质可得:.
故选:C.
2.B
【详解】解:由中心对称图形的定义:“把一个图形绕一个点旋转180°后,能够与自身完全重合,这样的图形叫做中心对称图形”
根据定义,A、C、D都不是中心对称图形,只有B是中心对称图形.
故选:B.
3.D
【分析】根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2,求出x=a,得出CD=a,代入求出即可.
【详解】解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,
∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,
设OC=a,则CN=2a,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,
x=a,
即CD=CM=a,
∴==,
故选:D.
【点睛】本题考查了等腰直角三角形性质,勾股定理,含30度角的直角三角形性质,旋转性质,三角形的内角和定理等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但有一定的难度.
4.D
【分析】本题是一个矩形绕着它的一边旋转一周,根据面动成体的原理即可解.
【详解】解:以矩形的一边所在直线为旋转轴,形成的旋转体叫做圆柱体.
故选:D.
【点睛】本题的考点是点、线、面、体;方法:一般来说,本节的内容只有圆柱,圆锥,球,圆柱是由长方形或正方形沿着一边旋转一周而成,圆锥是由直角三角形沿着一条直角边为旋转轴形成,球是由半圆沿着直径为旋转轴形成.
5.A
【分析】根据平移是某图形沿某一直线方向移动一定的距离,平移不改变图形的形状和大小,逐一判断即可得答案.
【详解】A.小亮在荡秋千的运动过程中,方向不断发生变化,故该选项不是平移运动,符合题意,
B.拉开抽屉的运动,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
C.站在运行的电梯上的人,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
D.坐在直线行驶的列车上的乘客,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
故选:A.
【点睛】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转.
6.D
【分析】根据旋转的定义进行分析即可解答
【详解】解:根据旋转的性质,旋转前后,各点的相对位置不变,得到的图形全等,
分析选项,可得正方形图案绕中心O旋转180°后,得到的图案是D.
故选D.
【点睛】本题考查了图纸旋转的性质,熟练掌握是解题的关键.
7.A
【分析】根据轴对称与中心对称图形的性质即可得出结论.
【详解】解:∵五星红旗上的五角星是等腰三角形,
∴五星红旗上的每一个五角星是轴对称图形,但不是中心对称图形.
故选:A.
【点睛】考点:中心对称图形;轴对称图形.
8.A
【详解】试题解析:如图,
有2种方法.
故选A.
9.D
【分析】如图,根据△AMC≌△QPE≌△BPD,可知PM=AB,利用勾股定理可得答案.
【详解】解:如图,经过点P、Q的直线则把它剪成了面积相等的两部分,
由图形可知△AMC≌△QPE≌△BPD,
∴AM=PB,
∴PM=AB,
∵,
∴,
故选:D.
【点睛】本题主要考查了图形的剪拼,全等三角形的判定与性质,勾股定理等知识,正确画出分割线是解题的关键.
10.D
【分析】观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【详解】解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
【点睛】此题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转角度叫做旋转角.
11.B
【详解】∵在△ABC中,∠B=90°,∠C=30°,AB=1,
∴AC=2.
∵将△ABC绕顶点A旋转180°,点C落在C′处,AC′=AC=2,
∴CC′=4.
故选B.
12.B
【分析】把扇形CDF平移到扇形BFE,我们会发现阴影部分的面积正好是长方形面积的一半,即等于2×2的正方形的面积
【详解】阴影部分面积=长方形面积的一半.
故阴影部分面积=2×2=4
故选B.
【点睛】此题考查平移的性质,解题关键在于发现平移后阴影部分的面积正好是长方形面积的一半
13.
【详解】试题分析:点向右平移4个单位,向下平移3个单位与原点重合,故点也如此平移,平移后为.
考点:点的平移和坐标的变化.
14.(﹣5,3)
【详解】试题分析:∵5的相反数是﹣5,﹣3的相反数是3,
∴点P(5,﹣3)关于原点的对称点的坐标为 (﹣5,3),
故答案为(﹣5,3).
考点:关于原点对称的点的坐标.
15.或
【详解】当点在点的左侧时,如图①.
,.,.当点在点的右侧时,如图②.,,.,,.综上,当时,的度数为或.
图① 图②
16.150
【分析】根据平移的性质可得:小桥总长就等于长方形荷塘的长与宽的和.
【详解】解:由平移的性质得,小桥总长=长方形周长的一半,
∵300÷2=150(m),
∴小桥总长为150m.
故答案为:150.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
17.
【详解】∵圆、矩形、菱形、正方形是中心对称图案,
∴抽到有中心对称图案的卡片的概率是,
故答案为:.
18.26° 74° 80° 80°
【详解】因为△DEF由△ABC平移得到,所以∠1=∠A=26°,∠2=∠E=74°(平移前后对应角相等).在△ABC中,∠C=180°-∠A-∠2=180°-26°-74°=80°,所以∠F=∠C=80°(平移前后对应角相等).
19.见解析
【详解】本题考查的是平移变换作图
根据“先向左平移6个格,再向下平移8个格”的要求找到各点的对应点,再顺次连接即可.
如图所示,
20.(1)见详解.
(2)60°.
【分析】(1)根据等边三角形性质得出,求出,根据推出,即可得到答案;
(2)证明,得到,根据三角形的内角和定理,即可解答.
【详解】(1)证明:和为等边三角形,
,
,
在和中,
,
,
;
(2)解:和都是等边三角形,
,
,
即,
在和中,,
,
,
,
.
故答案为:.
【点睛】本题考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.
21.(1)平行且相等
(2)
(3)
【分析】(1)由题意得:线段与线段的关系为平行且相等;
(2)由平移知,,则,因为三角形的面积=三角形的面积,推出四边形的面积=四边形的面积,利用梯形面积公式求解即可;
(3)由平移知,,,则,再利用平等线的性质以及角的和与差求解即可.
【详解】(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
【点睛】本题考查平移的性质,三角形的面积,解题的关键是掌握相关知识.
22.(1)建坐标系见详解,
(2)作图见详解,、、
(3)3
(4)存在,P点坐标为:或
【分析】(1)将A点坐标向右平移2个单位,再向上平移一个单位即可找到直角坐标系的坐标原点O,即可建立坐标系,则B点坐标可得;
(2)根据题目给出的平移方法作图即可;
(3)直接利用三角形面积公式即可求解;
(4)结合网格图和、的坐标可知,AC⊥y轴,AC=3,根据P点在y轴上,有PG⊥AC,结合面积可得PG=2,则问题得解.
【详解】(1)作图如下,
直角坐标系xoy如图所示,由图可知B点坐标为;
(2)作图如下:
即为所求,由图可知:、、;
(3)结合网格图,可知,
即△ABC的面积为3;
(4)存在,理由如下:
如图,AC交y轴于点G,
结合网格图和、的坐标可知,AC⊥y轴,AC=3,
∵P点在y轴上,
∴PG⊥AC,
∵,AC=3,
∴PG=2,
即如图,当P点在和时,满足PG=2,
由图可知此时坐标为:和,
即存在这样的P点,且P点坐标为:或.
【点睛】本题考查了利用平移变换作图,熟练掌握网格结构,准确找出坐标原点并建立直角坐标系是解题的关键.
23.(1)相等,(2)△DCF能与△BCE重合;(3)BE⊥DF
【分析】(1)相等,根据正方形的性质和已知条件证明△DCF≌△BCE即可;
(2)能,根据(1)可得结论;
(3)BE⊥DF.延长BE交DC于M,证明∠DME=90°即可.
【详解】解:(1)相等;
∵四边形ABCD是正方形,
∴BC=CD,∠DCF=∠BCE=90°,
在△DCF和△BCE中,
,
∴△DCF≌△BCE,
∴∠FDC=∠EBC,
故答案为相等;
(2)∵△DCF≌△BCE,
∴△DCF能与△BCE重合,
故答案为能;
(3)垂直,
理由如下:延长BE交DC于M,
∵△DCF≌△BCE,
∴∠CDF=∠EBC,
∵∠EBC+∠BEC=90°,
∴∠CDF+∠DEM=90°,
∴∠DME=90°,
∴BE⊥DF,
故答案为垂直.
【点睛】本题考查了全等三角形的判定和性质以及垂直的判定,解本题的关键是△BCE≌△DCF的求证.
24.(1)
(2)
(3)
【分析】(1)由图可知,平行于y轴的线段上所有点的横坐标都是2,纵坐标y的取值范围是,进而可表示线段上任意一点的坐标;
(2)根据向上平移,横坐标不变纵坐标相加,得到线段平移后的线段上的任意一点的坐标;
(3)根据向左平移,纵坐标不变横坐标相加,得到线段平移后的线段上的任意一点的坐标.
【详解】(1)解:线段上任意一点的坐标可表示为;
(2)解:所得的线段如图,
线段上任意一点的坐标可表示为;
(3)解:所得的线段如图2,线段上任意一点的坐标可表示为.
【点睛】本题考查了坐标与图形变化-平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.也考查了学生的理解能力与知识的迁移能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章图形的平移与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在RtABC中,BAC=,将ABC绕点A顺时针旋转后得到A(点B的对应点是点,点C的对应点是点),连接C.若C=,则B的大小是( )
A.32° B.64° C.77° D.87°
2.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )
A. B.
C. D.
3.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为( )
A. B. C. D.
4.将长方形绕着它的一边旋转一周得到的立体图形是( )
A.正方体 B.长方体 C.棱柱 D.圆柱
5.在下列生活现象中,不是平移的是( )
A.小亮荡秋千的运动 B.拉开抽屉的运动
C.站在运行的电梯上的人 D.坐在直线行驶的列车上的乘客
6.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
A. B.
C. D.
7.五星红旗上的每一个五角星 ( )
A.是轴对称图形,但不是中心对称图形 B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形 D.既不是轴对称图形,也不是中心对称图形
8.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.2种 B.3种 C.4种 D.5种
9.如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A. B. C. D.
10.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转后,能与原图形完全重合的是( )
A. B. C. D.
11.如图,△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C′处,则CC′的长为( )
A. B.4 C. D.
12.如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为( )
A.2cm2 B.4cm2 C.6cm2 D.无法确定
二、填空题
13.在平面直角坐标系中,已知点、,现将线段向右平移,使与坐标原点重合,则平移后的坐标是 .
14.点关于原点的对称点的坐标为 .
15.如图,在和中,,将绕点顺时针旋转一定角度,当时,的度数是 .
16.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为 m.
17.有五张分别印有圆、等腰三角形、矩形、菱形、正方形图案的卡片(卡片中除图案不同外,其余均相同),现将有图案的一面朝下任意摆放,从中任意抽取一张,抽到有中心对称图案的卡片的概率是 .
三、解答题
18.如图所示,△ABC平移后得到了△DEF,D在AB上,若∠A=26°,∠E=74°,求∠1,∠2,∠F,∠C的度数.
19.如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移8个格.
20.已知:如图和都是等边角形.是延长线上一点,与相交于点.、相交于点,、相交于点.
(1)在图①中,求证:;
(2)当绕点沿逆时针方向旋转到图②时,________.
21.如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
22.在如图的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上;
(1)建立适当的平面直角坐标系,使A(﹣2,﹣1),C(1,﹣1),写出B点坐标;
(2)在(1)的条件下,将△ABC向右平移4个单位再向上平移2个单位,在图中画出平移后的,并分别写出、、的坐标;
(3)求△ABC的面积.
(4)在y轴上是否存在点P,使得△ACP的面积和△ABC的面积相等,若存在,直接写出点P的坐标.
23.已知如图,正方形ABCD中,E为CD边上一点,F为BC边上一点,CE=CF.
(1)∠FDC=∠EBC,相等吗?
(2)△DCF能与△BCE重合吗?
(3)BE与DF垂直吗?
24.如图,在直角坐标系中,平行于x轴的线段上所有点的纵坐标都是,横坐标x的取值范围是,则线段上任意一点的坐标可以用“”表示.
按照类似这样的规定,回答下面的问题:
(1)怎样表示线段上任意一点的坐标?
(2)把线段向上平移2.5个单位,作出所得的线段.线段上任意一点的坐标怎样表示?
(3)把线段向左平移3个单位,作出所得的线段.线段上任意一点的坐标怎样表示?
《第三章图形的平移与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D A D A A D D
题号 11 12
答案 B B
1.C
【详解】解:根据旋转可得:,
则,
则 ,
则,
则根据旋转图形的性质可得:.
故选:C.
2.B
【详解】解:由中心对称图形的定义:“把一个图形绕一个点旋转180°后,能够与自身完全重合,这样的图形叫做中心对称图形”
根据定义,A、C、D都不是中心对称图形,只有B是中心对称图形.
故选:B.
3.D
【分析】根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2,求出x=a,得出CD=a,代入求出即可.
【详解】解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,
∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,
设OC=a,则CN=2a,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,
x=a,
即CD=CM=a,
∴==,
故选:D.
【点睛】本题考查了等腰直角三角形性质,勾股定理,含30度角的直角三角形性质,旋转性质,三角形的内角和定理等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但有一定的难度.
4.D
【分析】本题是一个矩形绕着它的一边旋转一周,根据面动成体的原理即可解.
【详解】解:以矩形的一边所在直线为旋转轴,形成的旋转体叫做圆柱体.
故选:D.
【点睛】本题的考点是点、线、面、体;方法:一般来说,本节的内容只有圆柱,圆锥,球,圆柱是由长方形或正方形沿着一边旋转一周而成,圆锥是由直角三角形沿着一条直角边为旋转轴形成,球是由半圆沿着直径为旋转轴形成.
5.A
【分析】根据平移是某图形沿某一直线方向移动一定的距离,平移不改变图形的形状和大小,逐一判断即可得答案.
【详解】A.小亮在荡秋千的运动过程中,方向不断发生变化,故该选项不是平移运动,符合题意,
B.拉开抽屉的运动,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
C.站在运行的电梯上的人,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
D.坐在直线行驶的列车上的乘客,方向不变,图形的形状和大小不变,故该选项是平移运动,不符合题意,
故选:A.
【点睛】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转.
6.D
【分析】根据旋转的定义进行分析即可解答
【详解】解:根据旋转的性质,旋转前后,各点的相对位置不变,得到的图形全等,
分析选项,可得正方形图案绕中心O旋转180°后,得到的图案是D.
故选D.
【点睛】本题考查了图纸旋转的性质,熟练掌握是解题的关键.
7.A
【分析】根据轴对称与中心对称图形的性质即可得出结论.
【详解】解:∵五星红旗上的五角星是等腰三角形,
∴五星红旗上的每一个五角星是轴对称图形,但不是中心对称图形.
故选:A.
【点睛】考点:中心对称图形;轴对称图形.
8.A
【详解】试题解析:如图,
有2种方法.
故选A.
9.D
【分析】如图,根据△AMC≌△QPE≌△BPD,可知PM=AB,利用勾股定理可得答案.
【详解】解:如图,经过点P、Q的直线则把它剪成了面积相等的两部分,
由图形可知△AMC≌△QPE≌△BPD,
∴AM=PB,
∴PM=AB,
∵,
∴,
故选:D.
【点睛】本题主要考查了图形的剪拼,全等三角形的判定与性质,勾股定理等知识,正确画出分割线是解题的关键.
10.D
【分析】观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【详解】解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
【点睛】此题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转角度叫做旋转角.
11.B
【详解】∵在△ABC中,∠B=90°,∠C=30°,AB=1,
∴AC=2.
∵将△ABC绕顶点A旋转180°,点C落在C′处,AC′=AC=2,
∴CC′=4.
故选B.
12.B
【分析】把扇形CDF平移到扇形BFE,我们会发现阴影部分的面积正好是长方形面积的一半,即等于2×2的正方形的面积
【详解】阴影部分面积=长方形面积的一半.
故阴影部分面积=2×2=4
故选B.
【点睛】此题考查平移的性质,解题关键在于发现平移后阴影部分的面积正好是长方形面积的一半
13.
【详解】试题分析:点向右平移4个单位,向下平移3个单位与原点重合,故点也如此平移,平移后为.
考点:点的平移和坐标的变化.
14.(﹣5,3)
【详解】试题分析:∵5的相反数是﹣5,﹣3的相反数是3,
∴点P(5,﹣3)关于原点的对称点的坐标为 (﹣5,3),
故答案为(﹣5,3).
考点:关于原点对称的点的坐标.
15.或
【详解】当点在点的左侧时,如图①.
,.,.当点在点的右侧时,如图②.,,.,,.综上,当时,的度数为或.
图① 图②
16.150
【分析】根据平移的性质可得:小桥总长就等于长方形荷塘的长与宽的和.
【详解】解:由平移的性质得,小桥总长=长方形周长的一半,
∵300÷2=150(m),
∴小桥总长为150m.
故答案为:150.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
17.
【详解】∵圆、矩形、菱形、正方形是中心对称图案,
∴抽到有中心对称图案的卡片的概率是,
故答案为:.
18.26° 74° 80° 80°
【详解】因为△DEF由△ABC平移得到,所以∠1=∠A=26°,∠2=∠E=74°(平移前后对应角相等).在△ABC中,∠C=180°-∠A-∠2=180°-26°-74°=80°,所以∠F=∠C=80°(平移前后对应角相等).
19.见解析
【详解】本题考查的是平移变换作图
根据“先向左平移6个格,再向下平移8个格”的要求找到各点的对应点,再顺次连接即可.
如图所示,
20.(1)见详解.
(2)60°.
【分析】(1)根据等边三角形性质得出,求出,根据推出,即可得到答案;
(2)证明,得到,根据三角形的内角和定理,即可解答.
【详解】(1)证明:和为等边三角形,
,
,
在和中,
,
,
;
(2)解:和都是等边三角形,
,
,
即,
在和中,,
,
,
,
.
故答案为:.
【点睛】本题考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.
21.(1)平行且相等
(2)
(3)
【分析】(1)由题意得:线段与线段的关系为平行且相等;
(2)由平移知,,则,因为三角形的面积=三角形的面积,推出四边形的面积=四边形的面积,利用梯形面积公式求解即可;
(3)由平移知,,,则,再利用平等线的性质以及角的和与差求解即可.
【详解】(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
【点睛】本题考查平移的性质,三角形的面积,解题的关键是掌握相关知识.
22.(1)建坐标系见详解,
(2)作图见详解,、、
(3)3
(4)存在,P点坐标为:或
【分析】(1)将A点坐标向右平移2个单位,再向上平移一个单位即可找到直角坐标系的坐标原点O,即可建立坐标系,则B点坐标可得;
(2)根据题目给出的平移方法作图即可;
(3)直接利用三角形面积公式即可求解;
(4)结合网格图和、的坐标可知,AC⊥y轴,AC=3,根据P点在y轴上,有PG⊥AC,结合面积可得PG=2,则问题得解.
【详解】(1)作图如下,
直角坐标系xoy如图所示,由图可知B点坐标为;
(2)作图如下:
即为所求,由图可知:、、;
(3)结合网格图,可知,
即△ABC的面积为3;
(4)存在,理由如下:
如图,AC交y轴于点G,
结合网格图和、的坐标可知,AC⊥y轴,AC=3,
∵P点在y轴上,
∴PG⊥AC,
∵,AC=3,
∴PG=2,
即如图,当P点在和时,满足PG=2,
由图可知此时坐标为:和,
即存在这样的P点,且P点坐标为:或.
【点睛】本题考查了利用平移变换作图,熟练掌握网格结构,准确找出坐标原点并建立直角坐标系是解题的关键.
23.(1)相等,(2)△DCF能与△BCE重合;(3)BE⊥DF
【分析】(1)相等,根据正方形的性质和已知条件证明△DCF≌△BCE即可;
(2)能,根据(1)可得结论;
(3)BE⊥DF.延长BE交DC于M,证明∠DME=90°即可.
【详解】解:(1)相等;
∵四边形ABCD是正方形,
∴BC=CD,∠DCF=∠BCE=90°,
在△DCF和△BCE中,
,
∴△DCF≌△BCE,
∴∠FDC=∠EBC,
故答案为相等;
(2)∵△DCF≌△BCE,
∴△DCF能与△BCE重合,
故答案为能;
(3)垂直,
理由如下:延长BE交DC于M,
∵△DCF≌△BCE,
∴∠CDF=∠EBC,
∵∠EBC+∠BEC=90°,
∴∠CDF+∠DEM=90°,
∴∠DME=90°,
∴BE⊥DF,
故答案为垂直.
【点睛】本题考查了全等三角形的判定和性质以及垂直的判定,解本题的关键是△BCE≌△DCF的求证.
24.(1)
(2)
(3)
【分析】(1)由图可知,平行于y轴的线段上所有点的横坐标都是2,纵坐标y的取值范围是,进而可表示线段上任意一点的坐标;
(2)根据向上平移,横坐标不变纵坐标相加,得到线段平移后的线段上的任意一点的坐标;
(3)根据向左平移,纵坐标不变横坐标相加,得到线段平移后的线段上的任意一点的坐标.
【详解】(1)解:线段上任意一点的坐标可表示为;
(2)解:所得的线段如图,
线段上任意一点的坐标可表示为;
(3)解:所得的线段如图2,线段上任意一点的坐标可表示为.
【点睛】本题考查了坐标与图形变化-平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.也考查了学生的理解能力与知识的迁移能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
