1.4角平分线同步强化练习（含解析）

中小学教育资源及组卷应用平台
1.4角平分线
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，，平分，平分，点恰在上，下列结论：①；②点到、的距离相等；③；④中正确的有（ ）
A．①②③ B．①②③④ C．①② D．②
2．如图，在四边形ABCD中，AD//BC，若∠DAB的角平分线AE交CD于E，连接BE，且BE平分∠ABC，则以下命题不正确的是（ ）．
A． B．E为CD中点
C． D．
3．如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB，交BC于点D，DE⊥AB于点E，且AB＝6cm，则△DEB的周长为（　　）
A．4cm B．6cm C．8cm D．以上都不对
4．已知：如图，为三角形纸片内部一点，连接，沿把纸片剪成三个三角形：，再使在一条直线上，若顶点（相同点用进行区分）都在直线上，且，则点为的（ ）
A．三条中线的交点 B．三条角平分线的交点
C．三条高的交点 D．三条边的垂直平分线的交点
5．如图，在中，为上一点，，垂足为，，垂足为，，连接，为边上的点，连接且．下列结论：①；②；③．其中结论正确的序号是（ ）
A．①② B．②③ C．①③ D．①②③
6．如图，，，，若，则为（ ）
A．1 B．2 C．3 D．4
7．△ABC是一个任意三角形，用直尺和圆规作出∠A，∠B的平分线相交于点O，那么下列说法不正确的是（ ）
A．点O一定在△ABC的内部 B．∠D的平分线一定经过点O
C．点O到△ABC三边的距离一定相等 D．点O到△ABC的三个顶点的距离一定相等
8．如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于（ ）
A．10 B．7 C．5 D．4
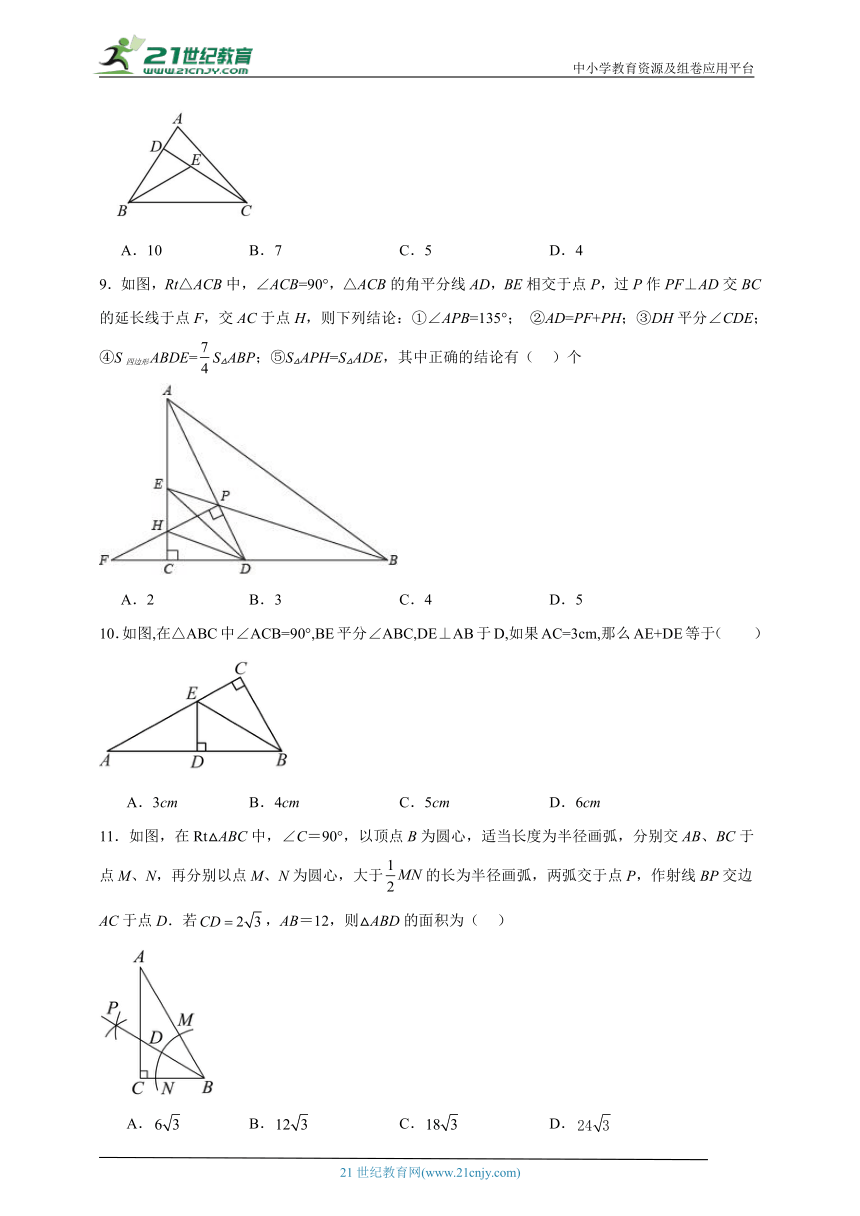
9．如图，Rt△ACB中，∠ACB=90°，△ACB的角平分线AD，BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB=135°； ②AD=PF+PH；③DH平分∠CDE；④S四边形ABDE=S△ABP；⑤S△APH=S△ADE，其中正确的结论有（ ）个
A．2 B．3 C．4 D．5
10．如图,在△ABC中∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于（　　）
A．3cm B．4cm C．5cm D．6cm
11．如图，在Rt△ABC中，∠C＝90°，以顶点B为圆心，适当长度为半径画弧，分别交AB、BC于点M、N，再分别以点M、N为圆心，大于的长为半径画弧，两弧交于点P，作射线BP交边AC于点D．若，AB＝12，则△ABD的面积为（ ）
A． B． C． D．
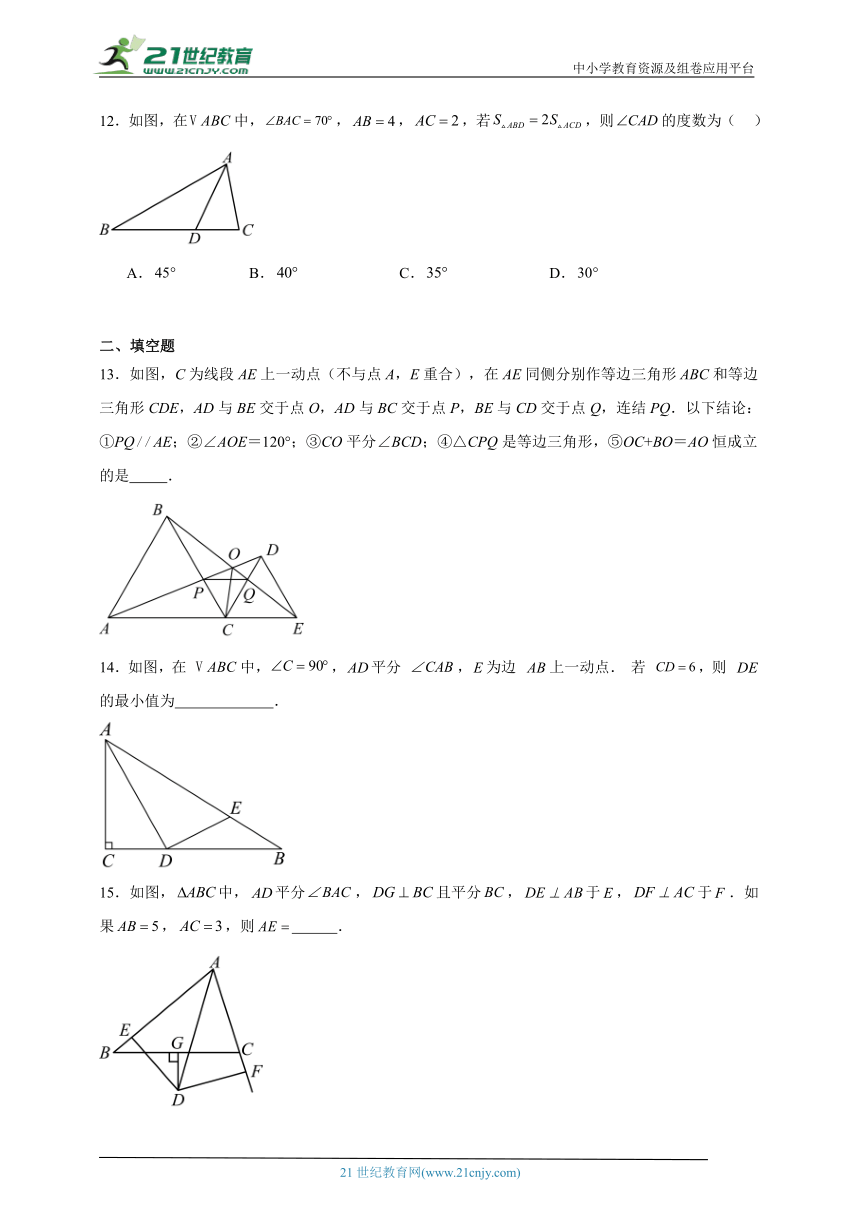
12．如图，在中，，，，若，则的度数为（ ）
A． B． C． D．
二、填空题
13．如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下结论：①PQAE；②∠AOE＝120°；③CO平分∠BCD；④△CPQ是等边三角形，⑤OC+BO＝AO恒成立的是 ．
14．如图，在 中，，平分 ，为边 上一动点． 若 ，则 的最小值为 ．

15．如图，中，平分，且平分，于，于．如果，，则 ．

16．如图，ABCD，以点A为圆心，小于AC的长为半径画弧，分别交AB、AC于E、F两点；再分别以E、F为圆心，大于的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠CMA＝25°，则∠C的度数为 °．
17．如图，点为的平分线上一点，过任作一直线分别与的两边交于，两点，为中点，过作的垂线交于点，，则 ．
三、解答题
18．如图，四边形中，为的角平分线，，、两点分别在、上，且．请完整说明为何四边形的面积为四边形的一半．
19．如图，在△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，CD=5cm，求AB的长．
20．在学习了利用尺规作一个角的平分线后，爱钻研的小聪发现，只有一把刻度尺也可以作出一个角的平分线．她是这样作的(如图)：
(1)分别在∠AOB的两边OA，OB上各取一点C，D，使得OC＝OD．
(2)连结CD，并量出CD的长度，取CD的中点E.
(3)过O，E两点作射线OE，则OE就是∠AOB的平分线．
请你说出小聪这样作的理由．
21．小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A=90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）M为边AC上一点，则BD、MF的位置是　 　．请你进行证明．
（2）M为边AC反向延长线上一点，则BD、MF的位置关系是　 　．请你进行证明．
（3）M为边AC延长线上一点，猜想BD、MF的位置关系是　 　．请你进行证明．
22．如图，点D在的边上，且．
(1)作的平分线，交于点E（保留作图痕迹，不写作法）；
(2)在（1）的条件下，，判断直线与直线的位置关系．
23．如图，点D是中的平分线和边的垂直平分线的交点，于点G，交的延长线于点H．
(1)点D到B，C两点的距离相等吗？为什么？
(2)点D到两边的距离相等吗？为什么？
(3)猜想和之间的大小关系，并证明你的结论．
24．如图，∠B=∠C=90°，E是BC的中点，AE平分∠BAD，求证：AE⊥DE.
《1.4角平分线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B A B D C B A
题号 11 12
答案 B C
1．B
【分析】本题考查了全等三角形的判定及性质的运用，角平分线的性质的运用，平行线的性质的运用．由平行线的性质及角平分线定义得出，，，那么，，判断结论①正确；由平分，平分，根据角平分线的性质得出点到，，的距离相等，判断结论②正确；延长，与的延长线交于点．利用证明，得出．再根据证明，得出，，判断结论③正确；由是的垂直平分线，得出，再根据，，判断结论④正确．
【详解】解：在四边形中，，平分，平分，
，，，
，
，故结论①正确；
平分，
点到，的距离相等，
平分，
点到，的距离相等，
点到，的距离相等，故结论②正确；
如图，延长，与的延长线交于点．
在和中，
，
，
．
∵，
，．
在和中，
，
，
，，故结论③正确；
，，
是的垂直平分线，
，
，，
，故结论④正确．
故选：B．
2．D
【分析】利用两直线平行，同旁内角互补，等腰三角形的判定与性质，三角形的全等推理判断即可.
【详解】如图,延长AE，BC二线交于点F，
∵AD//BC，AE平分∠DAB，BE平分∠ABC，
∴2∠ABE+2∠BAE=180°，
∴∠ABE+∠BAE=90°，
∴，
∴选项C正确；
∵AD//BC，AE平分∠DAB，
∴∠F=∠DAF=∠BAF，
∴AB=BF，
∵，
∴AE=EF，
∵∠AED=∠FEC，
∴△AED≌△FEC，
∴CE=ED，
∴E为CD的中点，
∴选项B正确；
∵△AED≌△FEC，
∴CF=AD，
∵BF=BC+CF，
∴BF=BC+AD，
∴AB=BC+AD，
∴选项A正确；
无法证明BC=CE，
∴选项D错误；
故选D.
【点睛】本题考查了平行线的性质，等腰三角形的判定与性质，三角形的全等，直角两个锐角互余，熟练运用上述性质，会延长二线的辅助线是解题的关键.
3．B
【分析】根据角平分线上的点到角的两边的距离相等可得CD＝DE，根据全等三角形对应边相等可得AC＝AE, 求出△DEB的周长＝AB．
【详解】解：∵AD平分∠CAB，∠C＝90°，DE⊥AB，
∴CD＝DE，
在△ACD和△AED中，，
∴△ACD≌△AED（HL），
∴AC＝AE，
∴可得△DEB的周长＝BD+DE+BE，
＝BD+CD+BE，
＝BC+BE，
＝AC+BE，
＝AE+BE，
＝AB，
∵AB＝6cm，
∴△DEB的周长为6cm．
故选：B．
【点睛】角平分线上的点到角的两边的距离相等与根据HL证明全等，等量代换理清逻辑。
4．B
【分析】本题主要考查了平行线的性质、角平分线的判定定理等知识点，掌握平行线上的两点距离相等成为解题的关键．
根据平行的性质可得点、到直线的距离相等，即点到的距离相等，然后根据角平分线的判定定理即可解答．
【详解】解：∵，
∴点、到直线的距离相等，即点到的距离相等，
∴点O为三条角平分线的交点．
故选B．
5．A
【分析】利用角平分线定理的逆定理可证平分，通过等量代换得出，即可证明，推出②正确；利用证明，可得，推出①正确；仅一组对边相等，一组对角相等不足以证明，推出③错误．
【详解】解：∵，，，
∴平分，
∴，
∵，
∴，
∴，故②正确；
在和中，
，
∴，
∴，故①正确；
∵和中，仅一组对边相等，一组对角相等，
∴现有条件不能够证明，故③错误；
综上，正确的是①②．
故选：A．
【点睛】本题考查全等三角形的判定与性质，角平分线定理的逆定理，平行线的判定等知识点，难度不大，能够综合运用上述知识点是解题的关键．
6．B
【分析】过点P作PM⊥OB于点M，根据平行线的性质可得到∠BCP的度数，再根据直角三角形的性质可求得PM的长，根据角平分线上的点到角两边的距离相等得到PM=PQ，从而求得PQ的长．
【详解】解：如图，过点P作PM⊥OB于点M，
∵，
∴ ，
∵，
∴ ，
∴ ，
∵PM⊥OB，，
∴ ，
∵，
∴ ．
故选：B．
【点睛】本题主要考查了含30°角的直角三角形的性质和平行线的性质；解决本题的关键就是利用角平分线的性质，把求PQ的长的问题进行转化．
7．D
【分析】根据角平分线的定义与性质即可判断．
【详解】∵三角形的三条角平分线在三角形内部且相交于一点，这一点到三角形三条边的距离相等，
∴A、B、C三个选项均正确，D选项错误．
故选D．
【点睛】本题考查了角平分线的性质定理，熟记角平分线的性质定理是解决问题的关键．
8．C
【详解】如图，过点E作EF⊥BC交BC于点F，根据角平分线的性质可得DE＝EF＝2，所以△BCE的面积等于，
故选：C．
9．B
【分析】①正确．利用三角形内角和定理以及角平分线的定义即可解决问题．
②正确．证明△ABP≌△FBP，推出PA=PF，再证明△APH≌△FPD，推出PH=PD即可解决问题．
③错误．利用反证法，假设成立，推出矛盾即可．
④错误，可以证明S四边形ABDE=2S△ABP．
⑤正确．由DH∥PE，利用等高模型解决问题即可．
【详解】解：在△ABC中，AD、BE分别平分∠BAC、∠ABC
∵∠ACB=90°
∴∠A+∠B=90°
又∵AD、BE分别平分∠BAC、∠ABC
∴∠BAD+∠ABE=（∠A+∠B）=45°
∴∠APB=135°，故①正确
∴∠BPD=45°
又∵PF⊥AD
∴∠FPB=90°+45°=135°
∴∠APB=∠FPB
又∵∠ABP=∠FBP
BP=BP
∴△ABP≌△FBP（ASA）
∴∠BAP=∠BFP，AB=FB，PA=PF
在△APH和△FPD中
∴△APH≌△FPD（ASA）
∴PH=PD
∴AD=AP+PD=PF+PH．故②正确
∵△ABP≌△FBP，△APH≌△FPD
∴S△APB=S△FPB，S△APH=S△FPD，PH=PD
∵∠HPD=90°
∴∠HDP=∠DHP=45°=∠BPD
∴HD∥EP
∴S△EPH=S△EPD
∴S△APH=S△AED，故⑤正确
∵S四边形ABDE=S△ABP+S△AEP+S△EPD+S△PBD
=S△ABP+（S△AEP+S△EPH）+S△PBD
=S△ABP+S△APH+S△PBD
=S△ABP+S△FPD+S△PBD
=S△ABP+S△FBP
=2S△ABP，故④不正确
若DH平分∠CDE，则∠CDH=∠EDH
∵DH∥BE
∴∠CDH=∠CBE=∠ABE
∴∠CDE=∠ABC
∴DE∥AB，这个显然与条件矛盾，故③错误
故选B．
【点睛】本题考查了角平分线的判定与性质，三角形全等的判定方法，三角形内角和定理，三角形的面积等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
10．A
【分析】关键角平分线的性质定理，得到EC=ED，即可推出AE+ED=AE+EC=AC，由此即可解决问题．
【详解】∵∠ACB=90°，
∴EC⊥CB，
又BE平分∠ABC，DE⊥AB，
∴CE=DE，
∴AE+DE=AE+CE=AC=3cm
故选A.
【点睛】此题考查角平分线的性质，解题关键在于掌握其性质.
11．B
【分析】过点D作DE⊥AB于点E，根据作图得出BD平分∠ABC，由角平分线的性质得出DE=DC，即可求出△ABD的面积．
【详解】解：过点D作DE⊥AB于点E，如图所示：
根据作图可知，BD平分∠ABC，
∵∠C=90°，
∴AC⊥BC，
∵DE⊥AB，
∴DE=DC，
，
∴，
∴，
故B正确．
故选：B．
【点睛】本题主要考查了角平分线的性质，解题的关键是作出辅助线，求出DE的长度．
12．C
【分析】作于点E，作于点F，根据可证，从而可知是的平分线，进而可求出的度数．
【详解】解：如图，作于点E，作于点F，
∵，
∴．
∵，，
∴
∴，
∴是的平分线．
∴．
故选C．
13．①②④⑤
【分析】由“”可证，可得，由“”可得，利用全等三角形的性质依次判断可求解．
【详解】解：等边和等边，
，，，
，即 ，
在与中，
，
，
，
又，
，即，
又，
，
，
又，
为等边三角形，故④正确；
，
，故①正确；
，
，故②正确；
如图，在上截取，连接，
，
，， ，
，
，，
，，
又，
，
，
，，
是等边三角形，
，
，故⑤正确；
不一定垂直，
不一定等于，
不一定等于，
不一定平分，故③错误；
故答案为：①②④⑤．
【点睛】本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质，能熟练应用相关性质是解题的关键．
14．
【分析】本题考查了角平分线的性质，根据垂线段最短，可得的最小值为，即可求解．
【详解】解：∵平分 ，，
∴当时，取得最小值，
此时，
故答案为：6．
15．4
【分析】连接，根据角平分线的性质可得，根据线段垂直平分线的性质，可得，继而可证得，可得，再证得，得到，设，由，即可得方程，解方程求出，进而可求得．
【详解】解：连接，，
平分，，，
，，
且平分，
，
在与中，
，
，
，
在和中，
，
，
，
设，则，
，，，，
，
解得：，
，
，
故答案为：4．
【点睛】此题考查了角平分线的性质、线段垂直平分线的性质以及全等三角形的判定与性质．准确作出辅助线，利用方程思想与数形结合思想求解是解决问题的关键．
16．130
【分析】直接利用平行线的性质结合角平分线的作法得出∠CAM=∠MAB=∠CMA=25°，再利用平行线的性质即可得出答案．
【详解】解：由作图知AP平分∠CAB，
∴∠CAM=∠MAB，
∵ABCD，
∴∠CMA=∠MAB=25°，
∴∠CAM=∠MAB=25°，
∴∠CAB=50°，
∵ABCD，
∴∠C=180°-∠CAB=130°．
故答案为：130．
【点睛】此题主要考查了角平分线的基本作图以及平行线的性质，正确得出∠CAM=∠MAB=∠CMA=25°是解题关键．
17．．
【分析】过D作DE⊥OM于E，DF⊥ON于F，根据角平分线性质求出DE＝DF，根据线段垂直平分线性质求出BD＝CD，证Rt△DEB≌Rt△DFC，求出∠EDB＝∠CDF，推出∠BDC＝∠EDF＝50°，由四边形内角和定理即可得出答案．
【详解】解：如图：
过作于，于，
则，
平分，
，
为中点，，
，
在和中，，
，
，
．，
；
故答案为：．
【点睛】本题考查了全等三角形的性质和判定，角平分线性质，线段垂直平分线性质的应用，能正确作出辅助线，证明三角形全等是解此题的关键．
18．详见解析
【分析】分别作于点，于点，由角平分线的性质得CG=CH，根据等底等高的三角形的面积相等得到△ABC面积=△ACD面积，又由于AE=DF，得到△AEC面积=△CDF面积，于是可求出△BCE面积=△ACF面积，由四边形AECF面积=△AEC面积+△ACF面积，四边形AECF面积=△AEC面积+△BCE面积，得到四边形AECF面积=△ABC面积，又由于四边形ABCD面积=△ABC面积+△ACD面积，四边形ABCD面积=2△ABC面积，即可得到结果．
【详解】解：分别作于点，于点，
∵为的角平分线，
∴．
∵，
∴面积面积．
又，
∴面积面积．
∴面积面积面积，面积面积面积．
∴面积面积．
∵四边形面积面积面积，面积面积面积，
∴四边形面积面积．
又四边形面积面积面积，
∴四边形面积面积，
∴四边形面积为四边形面积的一半．
【点睛】本题考查角平分线的性质，三角形的面积，解题的关键是正确的作出辅助线．
19．10cm
【分析】先有∠A=30°，那么∠ABC=60°，结合BD是角平分线，那么可求出∠DBC=∠ABD=30°，在Rt△DBC中，利用直角三角形中30°的角所对的直角边等于斜边的一半，可求出BD，再利用勾股定理可求BC，同理，在Rt△ABC中，AB=2BC，即可求AB．
【详解】解：在Rt△ABC中，∠C=90°，∠A=∠30°，
∴∠ABC=60°．
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD=30°．
∴∠ABD=∠BAD，
∴AD=DB，
在Rt△CBD中，CD=5cm，∠CBD=30°，
∴BD=10cm．
由勾股定理得，BC=5，
∴AB=2BC=10（cm）．
【点睛】本题利用了角平分线定义、直角三角形中30°的角所对的直角边等于斜边的一半、勾股定理等知识．
20．见解析
【详解】试题分析：本题考查了全等三角形的判定与性质及角平分线的定义.由作法可知OC＝OD，CE=CE从而根据根据全等三角形的判定方法“SSS”，可证△OCE≌△ODE，再由全等三角形的性质可得∠COE＝∠DOE，从而OE平分∠AOB.
解析：∵E是CD的中点，∴CE＝DE.
在△OCE和△ODE中，
,
∴△OCE≌△ODE(SSS)．
∴∠COE＝∠DOE，即OE是∠AOB的平分线．
21．（1）BD∥MF，理由详见解析；（2）BD⊥MF，理由详见解析；（3）BD⊥MF，理由详见解析.
【分析】（1）根据直角三角形的性质和平行线的判定即可得到答案.
（2）根据直角三角形的性质和角平分线的性质，及直角三角形的判定即可得到答案.
（3）根据直角三角形的性质和角平分线的性质，及垂直的判定即可得到答案.
【详解】解：（1）BD∥MF．
理由如下：∵∠A=90°，ME⊥BC，
∴∠ABC+∠AME=360°﹣90°×2=180°，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠ABC，∠AMF=∠AME，
∴∠ABD+∠AMF=（∠ABC+∠AME）=90°，
又∵∠AFM+∠AMF=90°，
∴∠ABD=∠AFM，
∴BD∥MF；
（2）BD⊥MF．
理由如下：∵∠A=90°，ME⊥BC，
∴∠ABC+∠C=∠AME+∠C=90°，
∴∠ABC=∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠AMF，
∵∠ABD+∠ADB=90°，
∴∠AMF+∠ADB=90°，
∴BD⊥MF；
（3）BD⊥MF．
理由如下：∵∠A=90°，ME⊥BC，
∴∠ABC+∠ACB=∠AME+∠ACB=90°，
∴∠ABC=∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠AMF，
∵∠AMF+∠F=90°，
∴∠ABD+∠F=90°，
∴BD⊥MF．
【点睛】本题主要考查直角三角形的性质、角平分线的性质和平行线的判定，解题的关键是熟练掌握直角三角形的性质、角平分线的性质和平行线的判定.
22．(1)见解析
(2)
【分析】本题考查了作角平分线，平行线的判定．熟练掌握作角平分线，平行线的判定是解题的关键．
（1）以为圆心，适当长为半径画弧交于，然后以为圆心，大于的长为半径画弧交点为，连接交于，即为所求；
（2）由平分可得，由，，可得，则，进而可得．
【详解】（1）解：如图，即为所求；
（2）解：∵平分，
∴，
∵，，
∴，
∴，
∴．
23．(1)相等．理由见解析
(2)相等．理由见解析
(3)．证明见解析
【分析】本题考查了线段垂直平分线及角平分线的性质，直角三角形全等的判定定理及性质，解答此题的关键是作出辅助线，构造出直角三角形解答．
（1）根据线段垂直平分线的性质解答即可；
（2）依据角平分线的性质解答；
（3）连接、，利用角平分线及线段垂直平分线的性质可求出，，依据定理可判断出，根据全等三角形的性质即可得出结论．
【详解】（1）相等．理由如下：
∵D是线段垂直平分线上的一点，
∴点D到B，C两点的距离相等．
（2）相等．理由如下：
∵点D在的平分线上，
∴点D到两边的距离相等．
（3）．证明：
如图，连接，．
∵D是线段垂直平分线上的点，
∴．
∵D是平分线上的点，，．
∴，
∴．
∴．
24．见解析
【分析】过点E作EF⊥AD于点F，由角平分线的性质可知EF=BE，由于E是BC的中点，所以CE=EB，所以EF=CE，再由角平分线的判定定理可知点E在∠CDA的平分线上，然后根据平行线的判定证出CD∥AB，从而证出∠BAD＋∠CDA=180°，结合角平分线的定义求出∠EAD＋∠EDA=90°，从而得出∠AED=90°，即可证出结论．
【详解】证明：如图，过点E作EF⊥AD于F，
∵∠B=90°，AE平分∠BAD，
∴EF=BE，∠EAD=∠BAD
∵E是BC的中点，
∴CE=EB，
∴EF=CE，
又∵∠C=90°，
∴点E在∠CDA的平分线上，
∴∠EDA=∠CDA
∵∠B=∠C=90°
∴∠B＋∠C=90°
∴CD∥AB
∴∠BAD＋∠CDA=180°
∴∠EAD＋∠EDA=∠BAD＋∠CDA
=（∠BAD＋∠CDA）
=90°
∴∠AED=90°
∴AE⊥DE．
【点睛】本题考查角平分线性质及判定、平行线的判定及性质和直角三角形的判定，熟练掌握角平分线性质及判定、平行线的判定及性质和直角三角形的判定是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)