3.2图形的旋转同步强化练习(含解析)
文档属性
| 名称 | 3.2图形的旋转同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 22:13:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.2图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
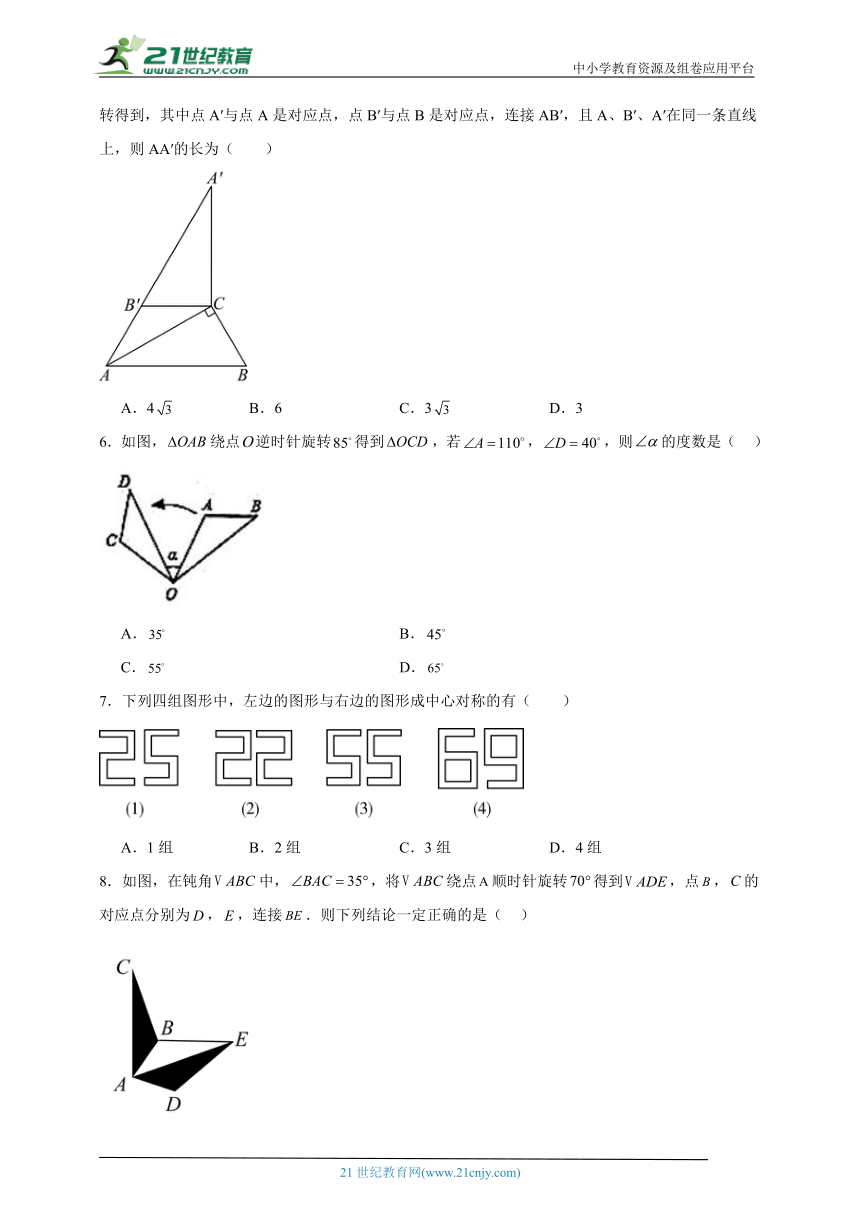
1.如图(1),已知两个全等三角形的直角顶点及一条直角边重合.将△ACB绕点C按顺时针方向旋转到的位置,其中交直线AD于点E,分别交直线AD、AC于点F、G,则在图(2)中,全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
2.如图,香港特别行政区标志紫荆花图案绕中心旋转°后能与原来的图案互相重合,则的最小值为( )
A.45 B.60 C.72 D.144
3.平面直角坐标系中,点A的坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到OA′,则点的坐标是( )
A.(4,-3) B.(-4,3) C.(3,-4) D.(-3,4)
4.如图,将三角形绕点A旋转到三角形,下列说法正确的个数有( )
(1);(2);(3);(4).
A.1个 B.2个 C.3个 D.4个
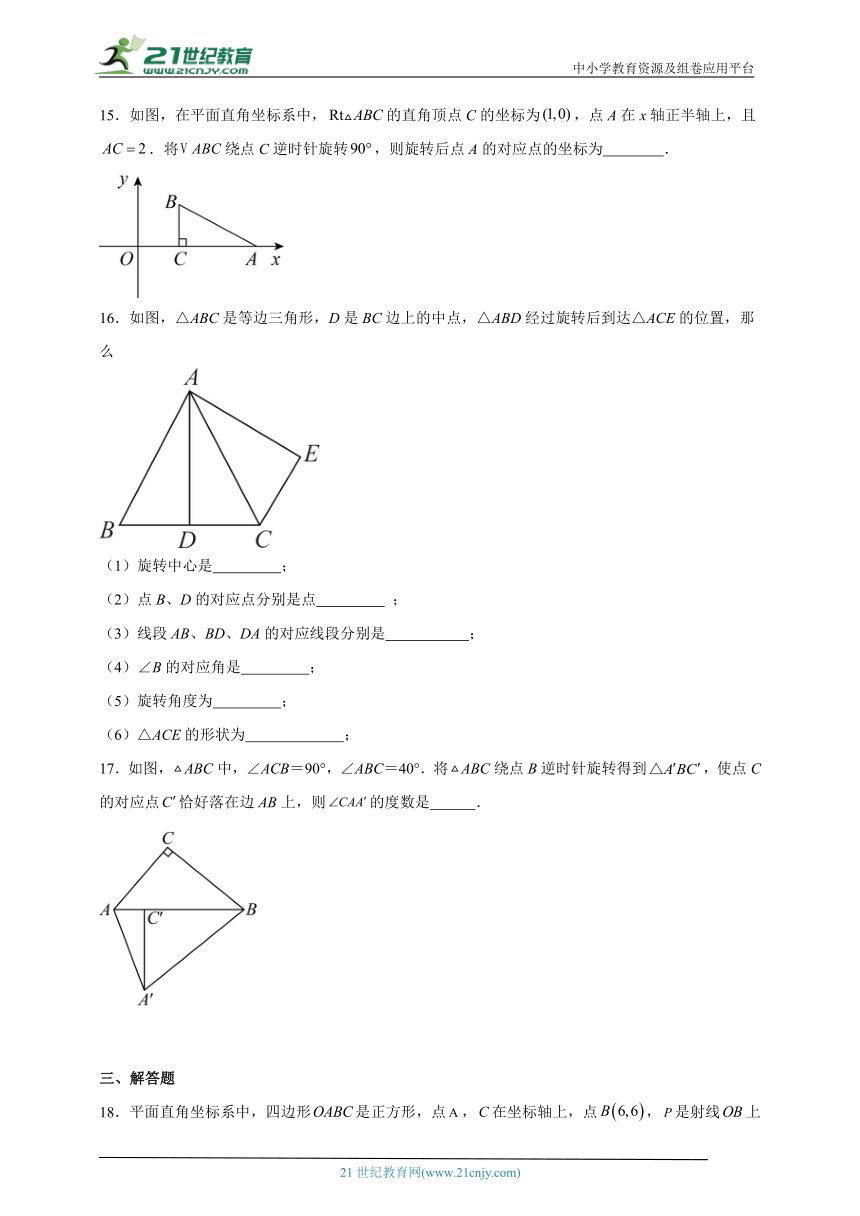
5.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.4 B.6 C.3 D.3
6.如图,绕点逆时针旋转得到,若,,则的度数是( )
A. B.
C. D.
7.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
8.如图,在钝角中,,将绕点顺时针旋转得到,点,的对应点分别为,,连接.则下列结论一定正确的是( )
A. B. C. D.平分
9.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
10.如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )
A. B. C. D.
11.已知点,将线段绕点A逆时针旋转得到线段,则点C的坐标为( )
A. B. C. D.
12.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是( )
A.正三角形 B.正方形 C.正六边形 D.正十边形
二、填空题
13.如图,在正方形网格中,线段AB绕某点顺时针旋转角α(0<α<180)得到线段A'B',点A与点A'是对应点,点B与点B'是对应点,则α等于 .
14.填空:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心是点 ,旋转角是∠ ,点A的对应点是点 .
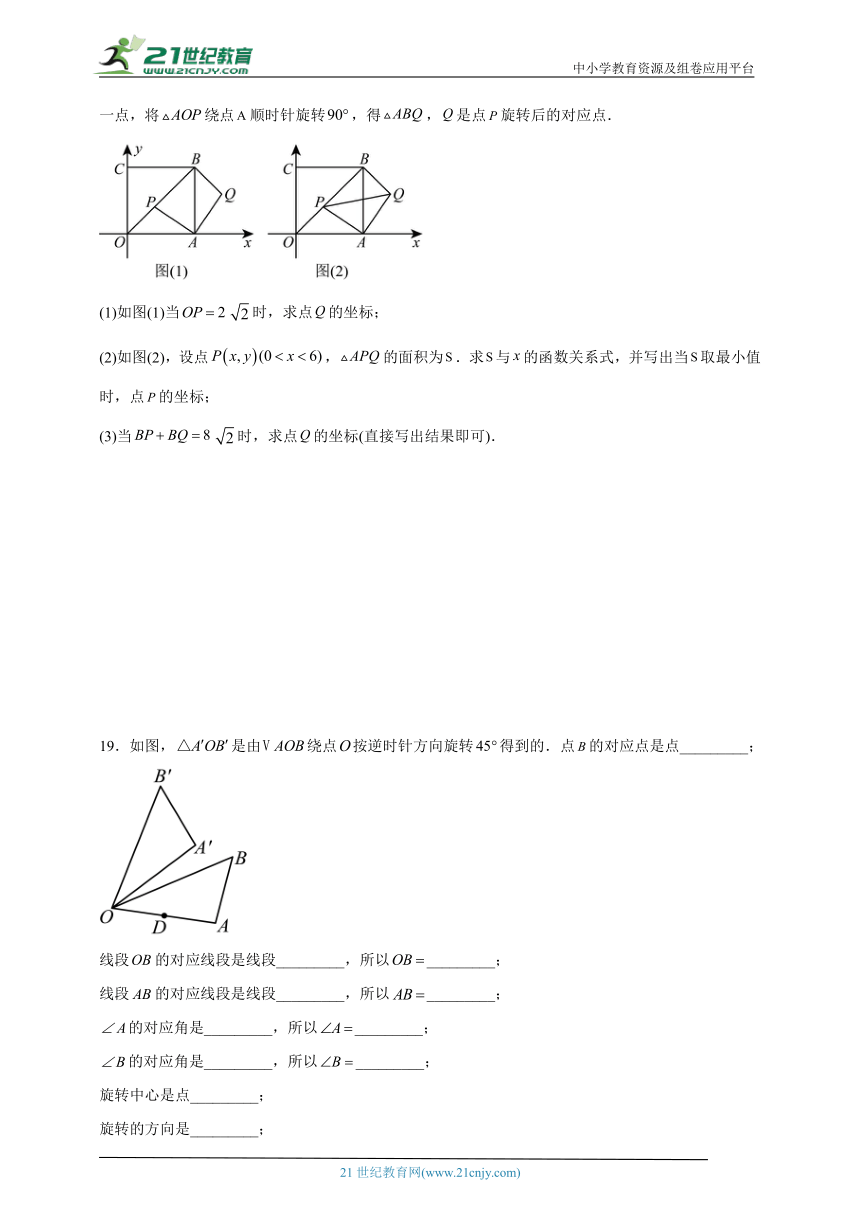
15.如图,在平面直角坐标系中,的直角顶点C的坐标为,点A在x轴正半轴上,且.将绕点C逆时针旋转,则旋转后点A的对应点的坐标为 .
16.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么
(1)旋转中心是 ;
(2)点B、D的对应点分别是点 ;
(3)线段AB、BD、DA的对应线段分别是 ;
(4)∠B的对应角是 ;
(5)旋转角度为 ;
(6)△ACE的形状为 ;
17.如图,ABC中,∠ACB=90°,∠ABC=40°.将ABC绕点B逆时针旋转得到,使点C的对应点恰好落在边AB上,则的度数是 .
三、解答题
18.平面直角坐标系中,四边形是正方形,点,在坐标轴上,点,是射线上一点,将绕点顺时针旋转,得,是点旋转后的对应点.
(1)如图(1)当时,求点的坐标;
(2)如图(2),设点,的面积为.求与的函数关系式,并写出当取最小值时,点的坐标;
(3)当时,求点的坐标(直接写出结果即可).
19.如图,是由绕点按逆时针方向旋转得到的.点的对应点是点_________;
线段的对应线段是线段_________,所以_________;
线段的对应线段是线段_________,所以_________;
的对应角是_________,所以_________;
的对应角是_________,所以_________;
旋转中心是点_________;
旋转的方向是_________;
旋转的角度是_________,写出一个等于此角度的角:_________;
的中点的对应点是_________的中点;
与的关系是_________.
20.将一副三角尺的直角重合放置(,),如图1所示,
(1)图1中的度数为 °;
(2)三角尺的位置保持不动,将三角尺绕其直角顶点顺时针方向旋转:
①当旋转至图2所示位置时,恰好,求此时的大小;
②若将三角尺继续绕旋转,直至回到图1位置,在这一过程中,是否会存在其中一边能与平行?如果存在,请你画出图形,并直接写出相应的的大小;如果不存在,请说明理由.
21.下图中的两个正方形的边长相等,请你指出可以通过绕点O旋转而相互得到的图形并说明旋转的角度.
22.已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
23.画出如图所示的四边形关于点成中心对称的四边形.
24.与均为等边三角形,在边上,连接.
(1)如图,若,,求的长;
(2)如图,若,在平面内将图中绕点顺时针旋转,连接、,交于点,连接,在运动过程中,猜想线段,,之间存在的数量关系,并证明你的猜想.
《3.2图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B C C D C B
题号 11 12
答案 D C
1.B
【详解】试题分析:根据旋转的性质和全等三角形的判定,有
≌△ACD,≌△FDC, ≌△ACE,≌△AGF.
共4对.故选B.
2.C
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是,并且圆具有旋转不变性,因而旋转的整数倍,就可以与自身重合.
【详解】该图形被平分成五部分,旋转的整数倍,就可以与自身重合,
故的最小值为.
故选:C
【点睛】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
3.B
【分析】根据旋转性质和坐标系内点的坐标特征即可解题.
【详解】见下图.在平面直角坐标系中找到A(3.4).连接OA.将线段OA绕原点O逆时针旋转90°得到OA′.读出A′.
【点睛】本题考查了图形的旋转.属于简单题.作图能力是解题关键.
4.C
【分析】图形旋转前后的对应边相等,对应角相等,根据旋转的性质解答.
【详解】解:据旋转的性质,可知:,故(1)错误;
,故(2)正确;
,故(3)正确;
,故(4)正确.
故选:C.
【点睛】此题考查旋转的性质:图形旋转前后的对应边相等,对应角相等,熟记性质是解题的关键.
5.B
【详解】试题分析:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6.
故选B.
考点:1、旋转的性质;2、直角三角形的性质
6.C
【分析】根据旋转的性质和三角形内角和180度求出【详解】解:根据旋转的性质可知:∠C=∠A=110°
在△COD中,∠COD=180°-110°-40°=30°
旋转角∠AOC=85°,所以∠α=85°-30°-55°
故选C.
【点睛】本题主要考查了旋转的性质,解题的关键是找准旋转角.
7.C
【详解】根据中心对称的定义可知,图(2)(3)(4)成中心对称,有3组,
故选C.
8.D
【分析】根据旋转可知△CAB≌△EAD,∠CAE=70°,结合∠BAC=35°,可知∠BAE=35°,则可证得△CAB≌△EAB,即可作答.
【详解】根据旋转的性质可知△CAB≌△EAD,∠CAE=70°,
∴∠BAE=∠CAE-∠CAB=70°-35°=35°,AC=AE,AB=AD,BC=DE,∠ABC=∠ADE,故A、B错误,
∴∠CAB=∠EAB,
∵AC=AE,AB=AB,
∴△CAB≌△EAB,
∴△EAB≌△EAD
∴∠BEA=∠DEA,
∴AE平分∠BED,故D正确,
∴AD+BE=AB+BE>AE=AC,故C错误,
故选:D.
【点睛】本题考查了旋转的性质和全等三角形的判定与性质,求出∠BAE=35°是解答本题的关键.
9.C
【分析】本题考查了生活中的旋转现象;旋转是围绕一点旋转一定的角度的图形变换,因而旋转一定有旋转中心和旋转角,且旋转前后图形能够重合,这时判断旋转的关键,根据旋转的定义解答即可.
【详解】解:A.坐在摩天轮里的小朋友,属于旋转,故不符合题意;
B.正在走动的时针,属于旋转,故不符合题意;
C.骑自行车的人,属于平移,故符合题意;
D.正在转动的风车叶片,属于旋转,故不符合题意;
故选:C.
10.B
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是72°,并且圆具有旋转不变性,因而旋转72度的整数倍,就可以与自身重合.
【详解】解:由该图形类同正五边形,正五边形的圆心角是.根据旋转的性质,当该图形围绕点O旋转后,旋转角是72°的倍数时,与其自身重合,否则不能与其自身重合.由于108°不是72°的倍数,从而旋转角是108°时,不能与其自身重合.
故选B.
【点睛】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
11.D
【分析】此题考查了图形的旋转,根据题意在坐标系中画出旋转后的图形,即可得到答案.
【详解】解:如图,将线段绕点A逆时针旋转得到线段,则点C的坐标为,
故选:D
12.C
【详解】解:A.正三角形的最小旋转角是120°,故此选项错误;
B.正方形的最小旋转角度是90°,故此选项错误;
C.正六边形的最小旋转角是60°,故此选项正确;
D.正十角形的最小旋转角是36°,故此选项错误;
故选C.
13.
【分析】先找出旋转中心,然后将对应点与旋转中心连线,再根据勾股定理逆定理判断旋转角的大小即可.
【详解】如图,连接AA',BB',作出AA'的垂直平分线,BB'的垂直平分线,两直线相交于点O,则点O为旋转中心,连接OA,OA',
假设每个方格的边长为1,
∵,,,
∴,
∴,
故答案为:.
【点睛】本题主要考查了图形旋转,熟练掌握相关作图方法是解决本题的关键.
14. O AOA′ A′
【详解】本题考查了旋转的性质. 旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.
根据旋转的定义即可得到杠杆绕支点转动撬起重物的旋转中心,旋转角和点A的对应点.
解:杠杆绕支点转动撬起重物,杠杆绕点O旋转,所以杠杆的旋转中心是点 O,旋转角是∠AOA′,点A的对应点是点 A′.
15.
【分析】画出示意图,然后根据旋转的性质可求得答案.
【详解】解:∵点C的坐标为,AC=2,
如图所示,将RtΔABC先绕点C逆时针旋转90°,
则点A'的坐标为,
故答案为:.
【点睛】本题考查了旋转变换,熟练掌握旋转的性质是解题的关键.
16. )点A 点C和点E AC、CE、EA ∠ACE 60° 直角三角形
【解析】略
17.120°
【分析】根据旋转可得∠A′BA=∠ABC=40°,A′B=AB,得∠BAA′=70°,根据∠CAA'=∠CAB+∠BAA′,进而可得∠CAA'的度数.
【详解】∵∠ACB=90°,∠ABC=40°,
∴∠CAB=90°﹣∠ABC=90°﹣40°=50°.
∵将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,
∴∠A′BA=∠ABC=40°,A′B=AB,
∴∠BAA′=∠BA′A=(180°﹣40°)=70°,
∴∠CAA'=∠CAB+∠BAA′=50°+70°=120°.
故答案为:120°.
【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理等知识,掌握旋转的性质是关键.
18.(1)
(2),当取最小值时,
(3)
【分析】(1)如图(1),过点作轴,垂足为,过点作轴,垂足为.证明.即可求点的坐标;
(2)如图(2),过点作轴,垂足为.根据勾股定理可得,根据,将解析式凑完全平方,根据非负数的性质求得最值即可求解;
(3)根据BP,可得.因为,说明点在的延长线上.可得.联立方程组可得和的长,结合(1)进而可求点的坐标.
【详解】(1)解:如图(1),过点作轴,垂足为,
过点作轴,垂足为.
四边形是正方形,
.
,
.
在中,
,
.
.
绕点顺时针旋转,得,
,,
,
,
,
.
,.
;
(2)如图(2),过点作轴,垂足为.
绕点顺时针旋转,得,
,.
,,
,
.
在中,根据勾股定理,
,
整理得.
,
.
当取最小值时,有,
;
(3).
理由如下:如图(3),
绕点旋转得到,
.
,
.
,
点在的延长线上.
.
由
解得:,.
,
,
同(1):,
,,
,
.
【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质、坐标与图形的性质-旋转、二元一次方程组、三角形的面积、勾股定理,解决本题的关键是综合运用以上知识.
19.见解析
【分析】根据题意旋转性质点的对应点是点,线段的对应线段是线段;线段的对应线段是线段;的对应角是;的对应角是;旋转中心是点;旋转的方向是逆时针;旋转的角度是,与的关系是全等.
【详解】解:是由绕点按逆时针方向旋转得到的,点的对应点是点,
线段的对应线段是线段,所以;线段的对应线段是线段,所以;的对应角是,所以;的对应角是,所以;旋转中心是点;旋转的方向是逆时针;旋转的角度是,写出一个等于此角度的角:;的中点的对应点是的中点;与的关系是全等.
故答案为:,,,,,,,,,,逆时针, ,(或),,全等.
【点睛】本题考查了旋转的基本概念,注意旋转前后的图形全等是解答本题的关键.
20.(1)165;(2) ①30°;②存在,图形见详解,.
【分析】(1)由已知可求出∠CAE=180°-60°=120°,再根据三角形外角性质求出∠BEC的度数.
(2)①由OD∥AB可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC.
②将三角板△COD继续绕O旋转,根据OC边、CD边与AB平行,利用平行线的性质即可求出∠AOC.
【详解】解:(1)∠CAE=180°-∠BAO=180°-60°=120°,
∴∠BEC=∠C+∠CAE=45°+120°=165°,
故答案为165°;
(2)①因为,所以;
所以;
所以;
②存在,如图1,∠AOC=120°;
如图2,∠AOC=165°;
如图3,∠AOC=30°;
如图4,∠AOC=150°;
如图5,∠AOC=60°;
如图6,∠AOC=15°.
故答案为(1)165;(2) ①30°;②存在,图形见详解,.
【点睛】本题考查平行线的性质及三角形的外角性质,解题的关键是根据三角形外角性质以及平行线的性质求解.
21.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°
【详解】试题分析:根据题意,我们首先要了解图形旋转的知识点,然后判断能旋转得到的图形,及旋转角.
试题解析:根据题意,可得△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,可通过旋转得到,旋转的角度为90°.
22.(1) 证明见解析
(2)成立,理由见解析
(3)或
【分析】(1)由旋转的性质可得BE=BF,∠EBF=,由“SAS”可证,可得∠BAE=∠BCF=,由直角三角形的性质可得结论;
(2)由旋转的性质可得BE=BF,∠EBF=,由“SAS”可证,可得∠BAE=∠BCF=,由直角三角形的性质可得结论;
(3)由全等三角形的性质和等边三角形的性质可得AB=AE,再分这情况讨论,结合等腰三角形的性质可求解.
【详解】(1)解:, 理由如下:
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=,
∵AB=AC,AD⊥BC,
∴,
∵将BE绕点B顺时针方向旋转得到BF,
∴BE=BF,∠EBF=,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴(SAS)
∴∠BAE=∠BCF=,
∴∠ACF=,
∴∠AFC+∠FAC=;
(2)(1)的结论仍然成立, 理由如下:
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=,
∵AB=AC,AD⊥BC,
∴∠BAD=,
∵将BE绕点B顺时针方向旋转得到BF,
∴BE=BF,∠EBF=,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴(SAS)
∴∠BAE=∠BCF=,
∴∠ACF=,
∴∠AFC+∠FAC=;
(3)如图,当点E在点A下方时,
∵△ACF是等腰直角三角形,
∴AC=CF,
∵△ABE≌△CBF,
∴CF=AE,
∴AC=AE=AB,
∴∠ABE=,
∴∠EBC=,
如图,当点E在点A上方时,
同理可得:
∴
∴∠EBC=.
【点睛】本题是几何变换综合题,考查了等边三角形的判定与性质,全等三角形的判定和性质,旋转的性质,灵活运用这些性质进行推理是本题的关键.
23.如图所示,四边形即为所求;见解析.
【分析】根据旋转的性质即可画出四边形ABCD关于点O成中心对称的四边形.
【详解】如图所示,四边形即为所求:
.
【点睛】本题考查了作图 旋转变换,解决本题的关键是掌握旋转的性质.
24.(1)
(2),证明见解析
【分析】(1)过点作交的延长线于,根据等边三角形性质,可以推出 ,从而得到,由勾股定理得到,再利用勾股定理即可求出长;
(2)由“”可证,可得,,,由面积法可得,可证平分,由“”可证,可得,即可求解.
【详解】(1)解:如图,过点作交的延长线于,
与均为等边三角形,
,,
,
,
,
,
,
在中,;
(2)解:,理由如下:
如图,过点作于,于,在上截取,连接,
与均为等边三角形,
,,,
,
在和中,
,
,
,,,
,
,
又,,
平分,
,
,
,
,
,
平分,
,
,
是等边三角形,
,,
,
在和中,
,
,
,
.
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的性质,勾股定理等知识,添加恰当辅助线构造全等三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图(1),已知两个全等三角形的直角顶点及一条直角边重合.将△ACB绕点C按顺时针方向旋转到的位置,其中交直线AD于点E,分别交直线AD、AC于点F、G,则在图(2)中,全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
2.如图,香港特别行政区标志紫荆花图案绕中心旋转°后能与原来的图案互相重合,则的最小值为( )
A.45 B.60 C.72 D.144
3.平面直角坐标系中,点A的坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到OA′,则点的坐标是( )
A.(4,-3) B.(-4,3) C.(3,-4) D.(-3,4)
4.如图,将三角形绕点A旋转到三角形,下列说法正确的个数有( )
(1);(2);(3);(4).
A.1个 B.2个 C.3个 D.4个
5.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.4 B.6 C.3 D.3
6.如图,绕点逆时针旋转得到,若,,则的度数是( )
A. B.
C. D.
7.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
8.如图,在钝角中,,将绕点顺时针旋转得到,点,的对应点分别为,,连接.则下列结论一定正确的是( )
A. B. C. D.平分
9.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
10.如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )
A. B. C. D.
11.已知点,将线段绕点A逆时针旋转得到线段,则点C的坐标为( )
A. B. C. D.
12.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是( )
A.正三角形 B.正方形 C.正六边形 D.正十边形
二、填空题
13.如图,在正方形网格中,线段AB绕某点顺时针旋转角α(0<α<180)得到线段A'B',点A与点A'是对应点,点B与点B'是对应点,则α等于 .
14.填空:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心是点 ,旋转角是∠ ,点A的对应点是点 .
15.如图,在平面直角坐标系中,的直角顶点C的坐标为,点A在x轴正半轴上,且.将绕点C逆时针旋转,则旋转后点A的对应点的坐标为 .
16.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么
(1)旋转中心是 ;
(2)点B、D的对应点分别是点 ;
(3)线段AB、BD、DA的对应线段分别是 ;
(4)∠B的对应角是 ;
(5)旋转角度为 ;
(6)△ACE的形状为 ;
17.如图,ABC中,∠ACB=90°,∠ABC=40°.将ABC绕点B逆时针旋转得到,使点C的对应点恰好落在边AB上,则的度数是 .
三、解答题
18.平面直角坐标系中,四边形是正方形,点,在坐标轴上,点,是射线上一点,将绕点顺时针旋转,得,是点旋转后的对应点.
(1)如图(1)当时,求点的坐标;
(2)如图(2),设点,的面积为.求与的函数关系式,并写出当取最小值时,点的坐标;
(3)当时,求点的坐标(直接写出结果即可).
19.如图,是由绕点按逆时针方向旋转得到的.点的对应点是点_________;
线段的对应线段是线段_________,所以_________;
线段的对应线段是线段_________,所以_________;
的对应角是_________,所以_________;
的对应角是_________,所以_________;
旋转中心是点_________;
旋转的方向是_________;
旋转的角度是_________,写出一个等于此角度的角:_________;
的中点的对应点是_________的中点;
与的关系是_________.
20.将一副三角尺的直角重合放置(,),如图1所示,
(1)图1中的度数为 °;
(2)三角尺的位置保持不动,将三角尺绕其直角顶点顺时针方向旋转:
①当旋转至图2所示位置时,恰好,求此时的大小;
②若将三角尺继续绕旋转,直至回到图1位置,在这一过程中,是否会存在其中一边能与平行?如果存在,请你画出图形,并直接写出相应的的大小;如果不存在,请说明理由.
21.下图中的两个正方形的边长相等,请你指出可以通过绕点O旋转而相互得到的图形并说明旋转的角度.
22.已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
23.画出如图所示的四边形关于点成中心对称的四边形.
24.与均为等边三角形,在边上,连接.
(1)如图,若,,求的长;
(2)如图,若,在平面内将图中绕点顺时针旋转,连接、,交于点,连接,在运动过程中,猜想线段,,之间存在的数量关系,并证明你的猜想.
《3.2图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B C C D C B
题号 11 12
答案 D C
1.B
【详解】试题分析:根据旋转的性质和全等三角形的判定,有
≌△ACD,≌△FDC, ≌△ACE,≌△AGF.
共4对.故选B.
2.C
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是,并且圆具有旋转不变性,因而旋转的整数倍,就可以与自身重合.
【详解】该图形被平分成五部分,旋转的整数倍,就可以与自身重合,
故的最小值为.
故选:C
【点睛】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
3.B
【分析】根据旋转性质和坐标系内点的坐标特征即可解题.
【详解】见下图.在平面直角坐标系中找到A(3.4).连接OA.将线段OA绕原点O逆时针旋转90°得到OA′.读出A′.
【点睛】本题考查了图形的旋转.属于简单题.作图能力是解题关键.
4.C
【分析】图形旋转前后的对应边相等,对应角相等,根据旋转的性质解答.
【详解】解:据旋转的性质,可知:,故(1)错误;
,故(2)正确;
,故(3)正确;
,故(4)正确.
故选:C.
【点睛】此题考查旋转的性质:图形旋转前后的对应边相等,对应角相等,熟记性质是解题的关键.
5.B
【详解】试题分析:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6.
故选B.
考点:1、旋转的性质;2、直角三角形的性质
6.C
【分析】根据旋转的性质和三角形内角和180度求出
在△COD中,∠COD=180°-110°-40°=30°
旋转角∠AOC=85°,所以∠α=85°-30°-55°
故选C.
【点睛】本题主要考查了旋转的性质,解题的关键是找准旋转角.
7.C
【详解】根据中心对称的定义可知,图(2)(3)(4)成中心对称,有3组,
故选C.
8.D
【分析】根据旋转可知△CAB≌△EAD,∠CAE=70°,结合∠BAC=35°,可知∠BAE=35°,则可证得△CAB≌△EAB,即可作答.
【详解】根据旋转的性质可知△CAB≌△EAD,∠CAE=70°,
∴∠BAE=∠CAE-∠CAB=70°-35°=35°,AC=AE,AB=AD,BC=DE,∠ABC=∠ADE,故A、B错误,
∴∠CAB=∠EAB,
∵AC=AE,AB=AB,
∴△CAB≌△EAB,
∴△EAB≌△EAD
∴∠BEA=∠DEA,
∴AE平分∠BED,故D正确,
∴AD+BE=AB+BE>AE=AC,故C错误,
故选:D.
【点睛】本题考查了旋转的性质和全等三角形的判定与性质,求出∠BAE=35°是解答本题的关键.
9.C
【分析】本题考查了生活中的旋转现象;旋转是围绕一点旋转一定的角度的图形变换,因而旋转一定有旋转中心和旋转角,且旋转前后图形能够重合,这时判断旋转的关键,根据旋转的定义解答即可.
【详解】解:A.坐在摩天轮里的小朋友,属于旋转,故不符合题意;
B.正在走动的时针,属于旋转,故不符合题意;
C.骑自行车的人,属于平移,故符合题意;
D.正在转动的风车叶片,属于旋转,故不符合题意;
故选:C.
10.B
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是72°,并且圆具有旋转不变性,因而旋转72度的整数倍,就可以与自身重合.
【详解】解:由该图形类同正五边形,正五边形的圆心角是.根据旋转的性质,当该图形围绕点O旋转后,旋转角是72°的倍数时,与其自身重合,否则不能与其自身重合.由于108°不是72°的倍数,从而旋转角是108°时,不能与其自身重合.
故选B.
【点睛】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
11.D
【分析】此题考查了图形的旋转,根据题意在坐标系中画出旋转后的图形,即可得到答案.
【详解】解:如图,将线段绕点A逆时针旋转得到线段,则点C的坐标为,
故选:D
12.C
【详解】解:A.正三角形的最小旋转角是120°,故此选项错误;
B.正方形的最小旋转角度是90°,故此选项错误;
C.正六边形的最小旋转角是60°,故此选项正确;
D.正十角形的最小旋转角是36°,故此选项错误;
故选C.
13.
【分析】先找出旋转中心,然后将对应点与旋转中心连线,再根据勾股定理逆定理判断旋转角的大小即可.
【详解】如图,连接AA',BB',作出AA'的垂直平分线,BB'的垂直平分线,两直线相交于点O,则点O为旋转中心,连接OA,OA',
假设每个方格的边长为1,
∵,,,
∴,
∴,
故答案为:.
【点睛】本题主要考查了图形旋转,熟练掌握相关作图方法是解决本题的关键.
14. O AOA′ A′
【详解】本题考查了旋转的性质. 旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.
根据旋转的定义即可得到杠杆绕支点转动撬起重物的旋转中心,旋转角和点A的对应点.
解:杠杆绕支点转动撬起重物,杠杆绕点O旋转,所以杠杆的旋转中心是点 O,旋转角是∠AOA′,点A的对应点是点 A′.
15.
【分析】画出示意图,然后根据旋转的性质可求得答案.
【详解】解:∵点C的坐标为,AC=2,
如图所示,将RtΔABC先绕点C逆时针旋转90°,
则点A'的坐标为,
故答案为:.
【点睛】本题考查了旋转变换,熟练掌握旋转的性质是解题的关键.
16. )点A 点C和点E AC、CE、EA ∠ACE 60° 直角三角形
【解析】略
17.120°
【分析】根据旋转可得∠A′BA=∠ABC=40°,A′B=AB,得∠BAA′=70°,根据∠CAA'=∠CAB+∠BAA′,进而可得∠CAA'的度数.
【详解】∵∠ACB=90°,∠ABC=40°,
∴∠CAB=90°﹣∠ABC=90°﹣40°=50°.
∵将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,
∴∠A′BA=∠ABC=40°,A′B=AB,
∴∠BAA′=∠BA′A=(180°﹣40°)=70°,
∴∠CAA'=∠CAB+∠BAA′=50°+70°=120°.
故答案为:120°.
【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理等知识,掌握旋转的性质是关键.
18.(1)
(2),当取最小值时,
(3)
【分析】(1)如图(1),过点作轴,垂足为,过点作轴,垂足为.证明.即可求点的坐标;
(2)如图(2),过点作轴,垂足为.根据勾股定理可得,根据,将解析式凑完全平方,根据非负数的性质求得最值即可求解;
(3)根据BP,可得.因为,说明点在的延长线上.可得.联立方程组可得和的长,结合(1)进而可求点的坐标.
【详解】(1)解:如图(1),过点作轴,垂足为,
过点作轴,垂足为.
四边形是正方形,
.
,
.
在中,
,
.
.
绕点顺时针旋转,得,
,,
,
,
,
.
,.
;
(2)如图(2),过点作轴,垂足为.
绕点顺时针旋转,得,
,.
,,
,
.
在中,根据勾股定理,
,
整理得.
,
.
当取最小值时,有,
;
(3).
理由如下:如图(3),
绕点旋转得到,
.
,
.
,
点在的延长线上.
.
由
解得:,.
,
,
同(1):,
,,
,
.
【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质、坐标与图形的性质-旋转、二元一次方程组、三角形的面积、勾股定理,解决本题的关键是综合运用以上知识.
19.见解析
【分析】根据题意旋转性质点的对应点是点,线段的对应线段是线段;线段的对应线段是线段;的对应角是;的对应角是;旋转中心是点;旋转的方向是逆时针;旋转的角度是,与的关系是全等.
【详解】解:是由绕点按逆时针方向旋转得到的,点的对应点是点,
线段的对应线段是线段,所以;线段的对应线段是线段,所以;的对应角是,所以;的对应角是,所以;旋转中心是点;旋转的方向是逆时针;旋转的角度是,写出一个等于此角度的角:;的中点的对应点是的中点;与的关系是全等.
故答案为:,,,,,,,,,,逆时针, ,(或),,全等.
【点睛】本题考查了旋转的基本概念,注意旋转前后的图形全等是解答本题的关键.
20.(1)165;(2) ①30°;②存在,图形见详解,.
【分析】(1)由已知可求出∠CAE=180°-60°=120°,再根据三角形外角性质求出∠BEC的度数.
(2)①由OD∥AB可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC.
②将三角板△COD继续绕O旋转,根据OC边、CD边与AB平行,利用平行线的性质即可求出∠AOC.
【详解】解:(1)∠CAE=180°-∠BAO=180°-60°=120°,
∴∠BEC=∠C+∠CAE=45°+120°=165°,
故答案为165°;
(2)①因为,所以;
所以;
所以;
②存在,如图1,∠AOC=120°;
如图2,∠AOC=165°;
如图3,∠AOC=30°;
如图4,∠AOC=150°;
如图5,∠AOC=60°;
如图6,∠AOC=15°.
故答案为(1)165;(2) ①30°;②存在,图形见详解,.
【点睛】本题考查平行线的性质及三角形的外角性质,解题的关键是根据三角形外角性质以及平行线的性质求解.
21.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°
【详解】试题分析:根据题意,我们首先要了解图形旋转的知识点,然后判断能旋转得到的图形,及旋转角.
试题解析:根据题意,可得△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,可通过旋转得到,旋转的角度为90°.
22.(1) 证明见解析
(2)成立,理由见解析
(3)或
【分析】(1)由旋转的性质可得BE=BF,∠EBF=,由“SAS”可证,可得∠BAE=∠BCF=,由直角三角形的性质可得结论;
(2)由旋转的性质可得BE=BF,∠EBF=,由“SAS”可证,可得∠BAE=∠BCF=,由直角三角形的性质可得结论;
(3)由全等三角形的性质和等边三角形的性质可得AB=AE,再分这情况讨论,结合等腰三角形的性质可求解.
【详解】(1)解:, 理由如下:
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=,
∵AB=AC,AD⊥BC,
∴,
∵将BE绕点B顺时针方向旋转得到BF,
∴BE=BF,∠EBF=,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴(SAS)
∴∠BAE=∠BCF=,
∴∠ACF=,
∴∠AFC+∠FAC=;
(2)(1)的结论仍然成立, 理由如下:
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=,
∵AB=AC,AD⊥BC,
∴∠BAD=,
∵将BE绕点B顺时针方向旋转得到BF,
∴BE=BF,∠EBF=,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴(SAS)
∴∠BAE=∠BCF=,
∴∠ACF=,
∴∠AFC+∠FAC=;
(3)如图,当点E在点A下方时,
∵△ACF是等腰直角三角形,
∴AC=CF,
∵△ABE≌△CBF,
∴CF=AE,
∴AC=AE=AB,
∴∠ABE=,
∴∠EBC=,
如图,当点E在点A上方时,
同理可得:
∴
∴∠EBC=.
【点睛】本题是几何变换综合题,考查了等边三角形的判定与性质,全等三角形的判定和性质,旋转的性质,灵活运用这些性质进行推理是本题的关键.
23.如图所示,四边形即为所求;见解析.
【分析】根据旋转的性质即可画出四边形ABCD关于点O成中心对称的四边形.
【详解】如图所示,四边形即为所求:
.
【点睛】本题考查了作图 旋转变换,解决本题的关键是掌握旋转的性质.
24.(1)
(2),证明见解析
【分析】(1)过点作交的延长线于,根据等边三角形性质,可以推出 ,从而得到,由勾股定理得到,再利用勾股定理即可求出长;
(2)由“”可证,可得,,,由面积法可得,可证平分,由“”可证,可得,即可求解.
【详解】(1)解:如图,过点作交的延长线于,
与均为等边三角形,
,,
,
,
,
,
,
在中,;
(2)解:,理由如下:
如图,过点作于,于,在上截取,连接,
与均为等边三角形,
,,,
,
在和中,
,
,
,,,
,
,
又,,
平分,
,
,
,
,
,
平分,
,
,
是等边三角形,
,,
,
在和中,
,
,
,
.
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的性质,勾股定理等知识,添加恰当辅助线构造全等三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
