14.3.1 扇形统计图、折线统计图、频数直方图 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 14.3.1 扇形统计图、折线统计图、频数直方图 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览


文档简介
14.3.1 扇形统计图、折线统计图、频数直方图
1. 能根据实际问题的特点,选择恰当的统计图表(扇形统计图、折线统计图、频数直方图)对数据进行可视化描述,认识各种统计图表的功能与作用.
2. 将图、表作为数学语言,运用于数据的表示、整理和分析,揭示蕴含其中的规律.
3. 体会合理使用统计图表的重要性.
活动一 扇形统计图、折线统计图
例1 据《中国统计年鉴(2015)》可知,1990年、2000年和2014年我国人口年龄分布情况(百分比)如下表所示.
年龄 年份
1990 2000 2014
0~14岁 27.7% 22.9% 16.5%
15~64岁 66.7% 70.1% 73.4%
65岁及以上 5.6% 7.0% 10.1%
(1) 试用扇形统计图表示2014年三个年龄段人口所占比;
(2) 试用折线统计图表示1990年、2000年和2014年65岁及以上人口占比.
扇形统计图能够直观地反应各个类别在总体中所占的比例,折线统计图可以看出变化趋势.
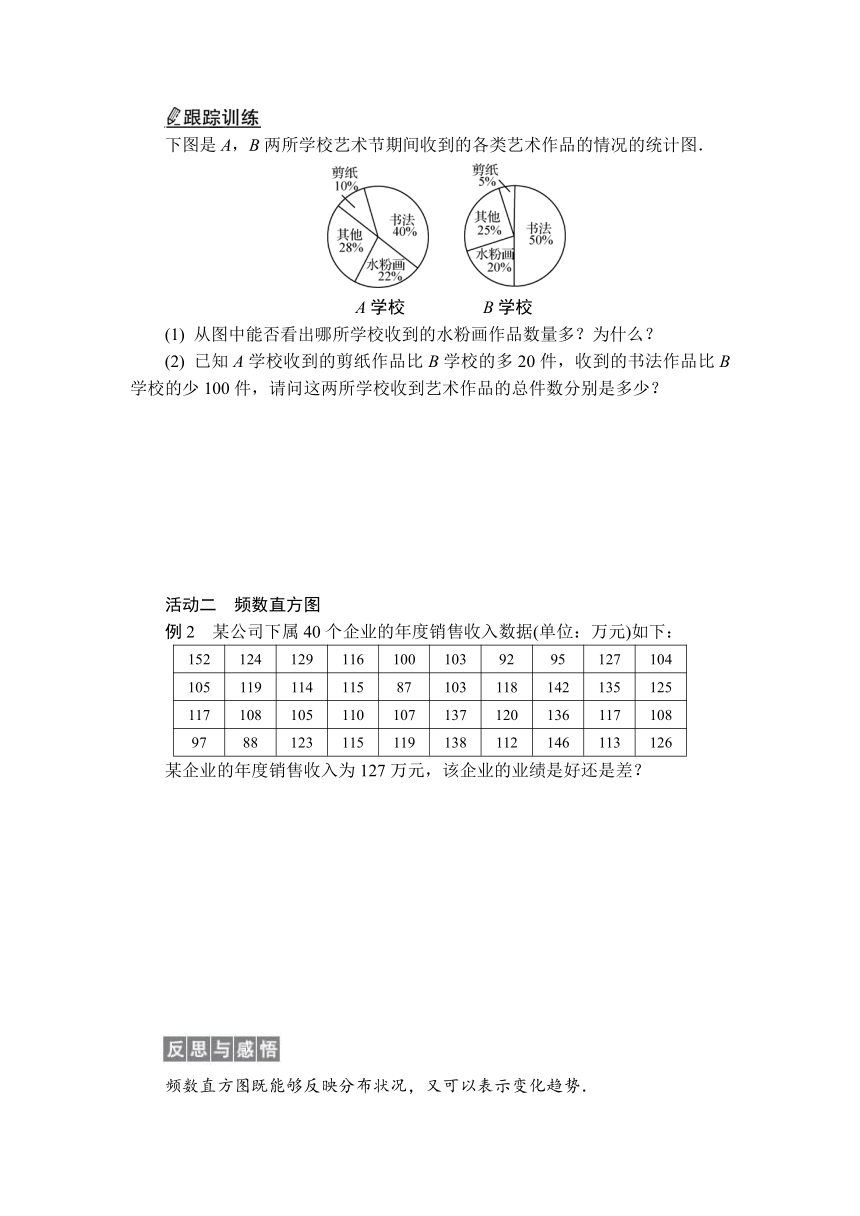
下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图.
A学校 B学校
(1) 从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总件数分别是多少?
活动二 频数直方图
例2 某公司下属40个企业的年度销售收入数据(单位:万元)如下:
152 124 129 116 100 103 92 95 127 104
105 119 114 115 87 103 118 142 135 125
117 108 105 110 107 137 120 136 117 108
97 88 123 115 119 138 112 146 113 126
某企业的年度销售收入为127万元,该企业的业绩是好还是差?
频数直方图既能够反映分布状况,又可以表示变化趋势.
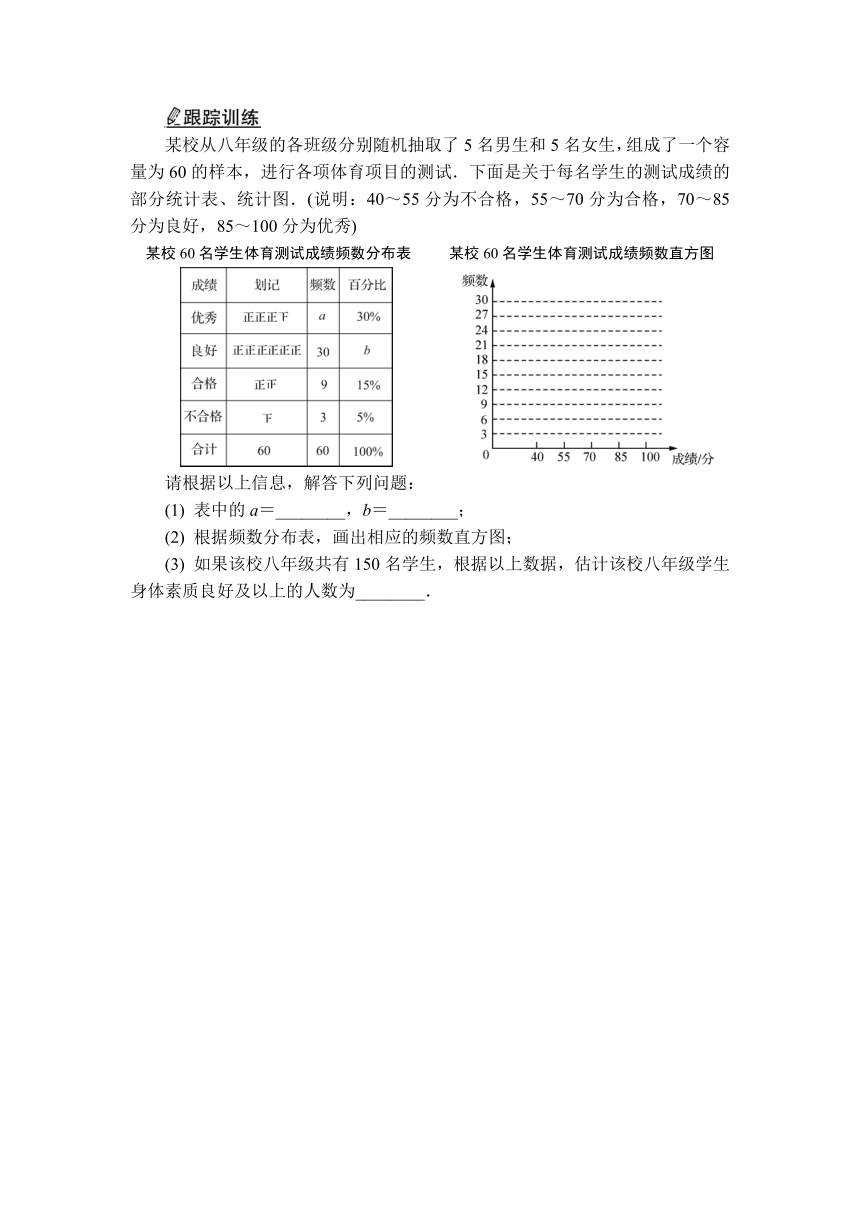
某校从八年级的各班级分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试.下面是关于每名学生的测试成绩的部分统计表、统计图.(说明:40~55分为不合格,55~70分为合格,70~85分为良好,85~100分为优秀)
某校60名学生体育测试成绩频数分布表 某校60名学生体育测试成绩频数直方图
请根据以上信息,解答下列问题:
(1) 表中的a=________,b=________;
(2) 根据频数分布表,画出相应的频数直方图;
(3) 如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为________.
1. (教材改编)某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2 000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的扇形图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则下列结论中正确的是( )
A. 这五个社团的总人数为100
B. 脱口秀社团的人数占五个社团总人数的20%
C. 这五个社团总人数占该校学生人数的8%
D. 脱口秀团在扇形统计图中所占圆心角的度数为90°
2. (2024湖南月考)如图为近一年我国商品零售总额和餐饮收入总额同比增速情况折线图,根据该图,下列结论中正确的是(注:同比,指当前的数据与上一年同期进行比对;环比,指当前数据与上个月的数据进行比对)( )
A. 2024年1~2月份,商品零售总额同比增长9.2%
B. 2023年3~12月份,餐饮收入总额同比都降低
C. 2023年6~10月份,商品零售总额同比都增加
D. 2023年12月,餐饮收入总额环比增速为-14.1%
3. (多选)(2024广东期中)2024年3月,树人中学组织三个年级的学生进行党史知识竞赛.经统计,得到前200名学生分布的扇形统计图和前200名中高一学生排名分布的频率条形图如图所示,则下列说法中正确的是( )
A. 成绩前200名的200人中,高一的人数比高二的人数多30
B. 成绩第1~100名的100人中,高一的人数不超过一半
C. 成绩第1~50名的50人中,高三最多有32人
D. 成绩第51~100名的50人中,高二的人数比高一的人数多
4. (教材改编)2023年6月6日是第二十八个全国爱眼日.某校为了做好学生的眼睛保护工作,对全体学生的裸眼视力进行了一次抽样调查,调查结果如图所示.根据学生视力合格标准,裸眼视力不低于5.0的为正常视力,则估计该校正常视力的学生占全体学生的________.
5. (2023湖南月考)某市为了增强学生体质,全面实施“学生饮用奶”营养工程. 某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶供学生饮用. 某中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如下两张不完整的统计图.
(1) 求本次被调查的学生有多少名?
(2) 补全下面的条形统计图,并计算出喜好菠萝味牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3) 该校共有1 200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味的多多少盒?
14.3.1 扇形统计图、折线统计图、频数直方图
【活动方案】
例1 (1) 2014年0~14岁、15~64岁和65岁及以上人口占比分别为16.5%,73.4%和10.1%,用扇形统计图表示如图所示.
(2) 1990年、2000年和2014年65岁及以上人口占比的折线统计图表示如图所示.
跟踪训练 (1) 不能.因为两所学校收到艺术作品的总数不知道.
(2) 设A学校收到艺术作品的总数为x件,B学校收到艺术作品的总数为y件,
则解得
即A学校收到艺术作品的总件数为500,B学校收到艺术作品的总件数为600.
例2 这就要看127在全部40个数据中所处的位置.为此,可以将这40个数据按每10(万)为一档(称为组距),用频率分布表表示.
分组 频数 频率
[80,90) 2 0.05
[90,100) 3 0.075
[100,110) 9 0.225
[110,120) 12 0.3
[120,130) 7 0.175
[130,140) 4 0.1
[140,150) 2 0.05
[150,160] 1 0.025
合计 40 1
从频率分布表可以看出,127位于[120,130)一档, 此档及比它高的档中的数据共14个,而低于这一档的数据有26个,故年销售收入为127万元的企业业绩还是比较好的.
我们还可以将此表“直观化”,作出频数直方图.
跟踪训练 (1) 18 50% 因为60×30%=18,所以a=18.因为30÷60×100%=50%,所以b=50%.
(2) 如图所示.
某校60名学生体育测试成绩频数直方图
(3) 120 150×(30%+50%)=120(人).
【检测反馈】
1. B 这五个社团的总人数为=80,=4%,故A错误,C错误;因为太极拳社团人数的占比为×10%=15%,所以脱口秀社团人数的占比为1-10%-15%-30%-25%=20%,所以脱口秀社团在扇形统计图中所占圆心角的度数为0.2×360°=72°,故B正确,D错误.
2. C 对于A,2024年1~2月份,商品零售总额同比增长2.9%,故A错误;对于B,2023年8月份,餐饮收入总额同比增加,故B错误;对于C,2023年6~10月份,商品零售总额同比都增加,故C正确;对于D,2023年12月,餐饮收入总额环比增速并未告知,故D错误.
3. ABC 由扇形统计图可知,成绩前200名的200人中,高一的人数比高二的人数多200×(45%-30%)=30,故A正确;由条形图知,成绩第1~200名的200人中,前100和后100的人数相等,因此高一的人数为200×45%×=45<50,故B正确;成绩第1~50名的50人中,高一的人数为200×45%×0.2=18,因此高三最多有32人,故C正确;成绩第51~100名的50人中,高一的人数为200×45%×0.3=27,因此高二最多有23人,一定比高一的人数少,故D错误.故选ABC.
4. 20% 该校正常视力的学生占全体学生的×100%=20%.
5. (1) 根据喜好核桃味的学生数,得本次被调查的学生数(样本容量)为10÷5%=200.
(2) 喜好香橙味牛奶的学生数是200-38-62-50-10=40,补全条形统计图如图所示.
喜好菠萝味牛奶的学生人数为50,
在扇形统计图中所占圆心角的度数为×360°=90°.
(3) 草莓味要比原味多×(62-38)=144(盒).
1. 能根据实际问题的特点,选择恰当的统计图表(扇形统计图、折线统计图、频数直方图)对数据进行可视化描述,认识各种统计图表的功能与作用.
2. 将图、表作为数学语言,运用于数据的表示、整理和分析,揭示蕴含其中的规律.
3. 体会合理使用统计图表的重要性.
活动一 扇形统计图、折线统计图
例1 据《中国统计年鉴(2015)》可知,1990年、2000年和2014年我国人口年龄分布情况(百分比)如下表所示.
年龄 年份
1990 2000 2014
0~14岁 27.7% 22.9% 16.5%
15~64岁 66.7% 70.1% 73.4%
65岁及以上 5.6% 7.0% 10.1%
(1) 试用扇形统计图表示2014年三个年龄段人口所占比;
(2) 试用折线统计图表示1990年、2000年和2014年65岁及以上人口占比.
扇形统计图能够直观地反应各个类别在总体中所占的比例,折线统计图可以看出变化趋势.
下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图.
A学校 B学校
(1) 从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总件数分别是多少?
活动二 频数直方图
例2 某公司下属40个企业的年度销售收入数据(单位:万元)如下:
152 124 129 116 100 103 92 95 127 104
105 119 114 115 87 103 118 142 135 125
117 108 105 110 107 137 120 136 117 108
97 88 123 115 119 138 112 146 113 126
某企业的年度销售收入为127万元,该企业的业绩是好还是差?
频数直方图既能够反映分布状况,又可以表示变化趋势.
某校从八年级的各班级分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试.下面是关于每名学生的测试成绩的部分统计表、统计图.(说明:40~55分为不合格,55~70分为合格,70~85分为良好,85~100分为优秀)
某校60名学生体育测试成绩频数分布表 某校60名学生体育测试成绩频数直方图
请根据以上信息,解答下列问题:
(1) 表中的a=________,b=________;
(2) 根据频数分布表,画出相应的频数直方图;
(3) 如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为________.
1. (教材改编)某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2 000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的扇形图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则下列结论中正确的是( )
A. 这五个社团的总人数为100
B. 脱口秀社团的人数占五个社团总人数的20%
C. 这五个社团总人数占该校学生人数的8%
D. 脱口秀团在扇形统计图中所占圆心角的度数为90°
2. (2024湖南月考)如图为近一年我国商品零售总额和餐饮收入总额同比增速情况折线图,根据该图,下列结论中正确的是(注:同比,指当前的数据与上一年同期进行比对;环比,指当前数据与上个月的数据进行比对)( )
A. 2024年1~2月份,商品零售总额同比增长9.2%
B. 2023年3~12月份,餐饮收入总额同比都降低
C. 2023年6~10月份,商品零售总额同比都增加
D. 2023年12月,餐饮收入总额环比增速为-14.1%
3. (多选)(2024广东期中)2024年3月,树人中学组织三个年级的学生进行党史知识竞赛.经统计,得到前200名学生分布的扇形统计图和前200名中高一学生排名分布的频率条形图如图所示,则下列说法中正确的是( )
A. 成绩前200名的200人中,高一的人数比高二的人数多30
B. 成绩第1~100名的100人中,高一的人数不超过一半
C. 成绩第1~50名的50人中,高三最多有32人
D. 成绩第51~100名的50人中,高二的人数比高一的人数多
4. (教材改编)2023年6月6日是第二十八个全国爱眼日.某校为了做好学生的眼睛保护工作,对全体学生的裸眼视力进行了一次抽样调查,调查结果如图所示.根据学生视力合格标准,裸眼视力不低于5.0的为正常视力,则估计该校正常视力的学生占全体学生的________.
5. (2023湖南月考)某市为了增强学生体质,全面实施“学生饮用奶”营养工程. 某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶供学生饮用. 某中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如下两张不完整的统计图.
(1) 求本次被调查的学生有多少名?
(2) 补全下面的条形统计图,并计算出喜好菠萝味牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3) 该校共有1 200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味的多多少盒?
14.3.1 扇形统计图、折线统计图、频数直方图
【活动方案】
例1 (1) 2014年0~14岁、15~64岁和65岁及以上人口占比分别为16.5%,73.4%和10.1%,用扇形统计图表示如图所示.
(2) 1990年、2000年和2014年65岁及以上人口占比的折线统计图表示如图所示.
跟踪训练 (1) 不能.因为两所学校收到艺术作品的总数不知道.
(2) 设A学校收到艺术作品的总数为x件,B学校收到艺术作品的总数为y件,
则解得
即A学校收到艺术作品的总件数为500,B学校收到艺术作品的总件数为600.
例2 这就要看127在全部40个数据中所处的位置.为此,可以将这40个数据按每10(万)为一档(称为组距),用频率分布表表示.
分组 频数 频率
[80,90) 2 0.05
[90,100) 3 0.075
[100,110) 9 0.225
[110,120) 12 0.3
[120,130) 7 0.175
[130,140) 4 0.1
[140,150) 2 0.05
[150,160] 1 0.025
合计 40 1
从频率分布表可以看出,127位于[120,130)一档, 此档及比它高的档中的数据共14个,而低于这一档的数据有26个,故年销售收入为127万元的企业业绩还是比较好的.
我们还可以将此表“直观化”,作出频数直方图.
跟踪训练 (1) 18 50% 因为60×30%=18,所以a=18.因为30÷60×100%=50%,所以b=50%.
(2) 如图所示.
某校60名学生体育测试成绩频数直方图
(3) 120 150×(30%+50%)=120(人).
【检测反馈】
1. B 这五个社团的总人数为=80,=4%,故A错误,C错误;因为太极拳社团人数的占比为×10%=15%,所以脱口秀社团人数的占比为1-10%-15%-30%-25%=20%,所以脱口秀社团在扇形统计图中所占圆心角的度数为0.2×360°=72°,故B正确,D错误.
2. C 对于A,2024年1~2月份,商品零售总额同比增长2.9%,故A错误;对于B,2023年8月份,餐饮收入总额同比增加,故B错误;对于C,2023年6~10月份,商品零售总额同比都增加,故C正确;对于D,2023年12月,餐饮收入总额环比增速并未告知,故D错误.
3. ABC 由扇形统计图可知,成绩前200名的200人中,高一的人数比高二的人数多200×(45%-30%)=30,故A正确;由条形图知,成绩第1~200名的200人中,前100和后100的人数相等,因此高一的人数为200×45%×=45<50,故B正确;成绩第1~50名的50人中,高一的人数为200×45%×0.2=18,因此高三最多有32人,故C正确;成绩第51~100名的50人中,高一的人数为200×45%×0.3=27,因此高二最多有23人,一定比高一的人数少,故D错误.故选ABC.
4. 20% 该校正常视力的学生占全体学生的×100%=20%.
5. (1) 根据喜好核桃味的学生数,得本次被调查的学生数(样本容量)为10÷5%=200.
(2) 喜好香橙味牛奶的学生数是200-38-62-50-10=40,补全条形统计图如图所示.
喜好菠萝味牛奶的学生人数为50,
在扇形统计图中所占圆心角的度数为×360°=90°.
(3) 草莓味要比原味多×(62-38)=144(盒).
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
