14.3.2 频率直方图 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 14.3.2 频率直方图 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 317.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 19:28:33 | ||
图片预览



文档简介
14.3.2 频率直方图
1. 能列出频率分布表,能画出频率直方图与频率折线图.
2. 学会用频率直方图研究数据的分布规律.
3. 能运用样本数据的频率直方图估计总体分布.
活动一 频率直方图与频率折线图的概念
思考
在频数直方图中,一般情况取相等的组距,其目的是什么?如果组距不等,会有什么影响?能否用其他的直方图来描述原来的数据?
1. 绘制频率直方图的一般步骤是什么?
2. 在频率直方图中,各个长方形的面积表示________.(填序号)
①落在相应各组的数据的频数;
②相应各组的频率;
③该样本所分成的组数;
④该样本的样本容量.
3. 将频率直方图中各个矩形的上底边的中点顺次连接起来,并将两边端点向外延伸半个组距,就得到频率折线图,简称折线图.
活动二 频率直方图与频率折线图的应用
例1 下表是100名学生身高(单位:cm)的频率分布表,根据数据画出频率直方图和频率折线图.
分组 频数累计 频数 频率
[150.5,153.5) 4 4 0.04
[153.5,156.5) 12 8 0.08
[156.5,159.5) 20 8 0.08
[159.5,162.5) 31 11 0.11
[162.5,165.5) 53 22 0.22
[165.5,168.5) 72 19 0.19
[168.5,171.5) 86 14 0.14
[171.5,174.5) 93 7 0.07
[174.5,177.5) 97 4 0.04
[177.5,180.5] 100 3 0.03
合计 100 1
频率直方图比频率分布表更直观、形象地反映了样本的分布规律.频率折线图的优点是它反映了数据的变化趋势.
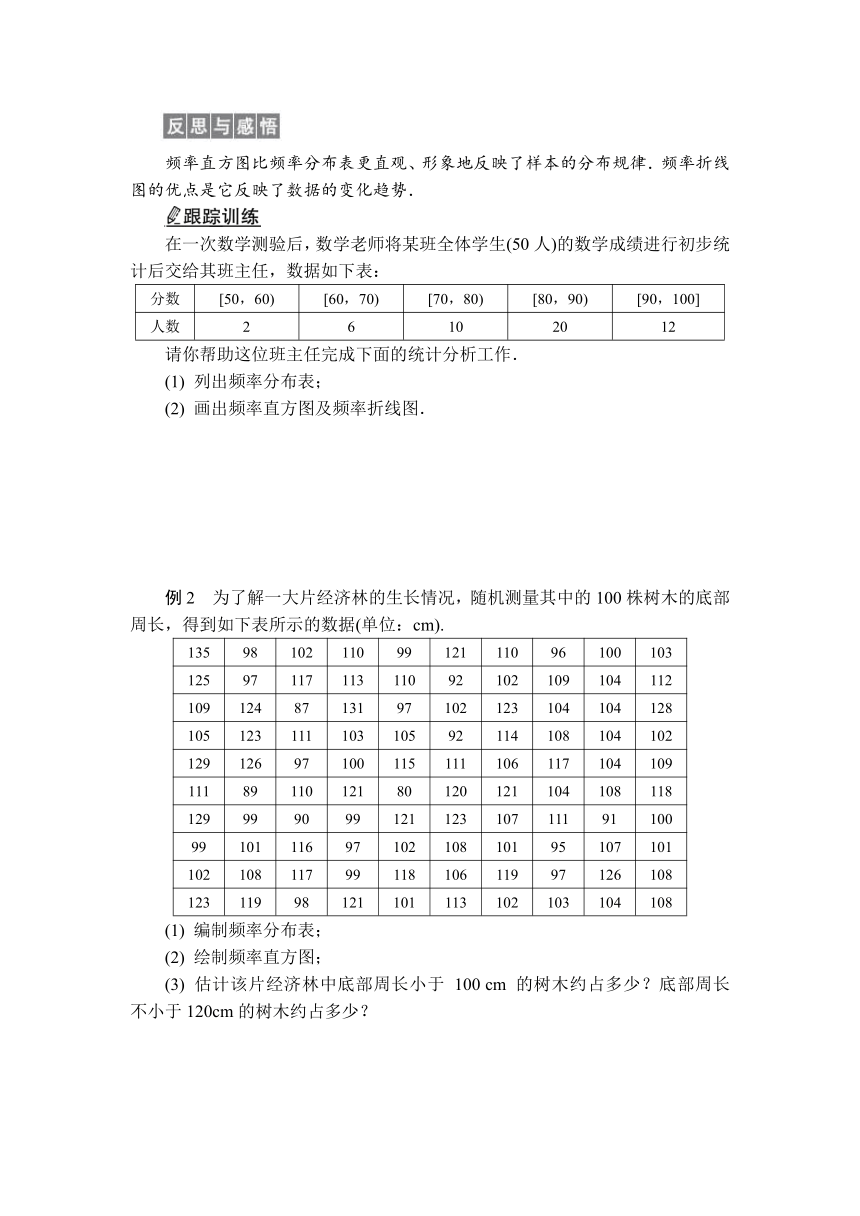
在一次数学测验后,数学老师将某班全体学生(50人)的数学成绩进行初步统计后交给其班主任,数据如下表:
分数 [50,60) [60,70) [70,80) [80,90) [90,100]
人数 2 6 10 20 12
请你帮助这位班主任完成下面的统计分析工作.
(1) 列出频率分布表;
(2) 画出频率直方图及频率折线图.
例2 为了解一大片经济林的生长情况,随机测量其中的100株树木的底部周长,得到如下表所示的数据(单位:cm).
135 98 102 110 99 121 110 96 100 103
125 97 117 113 110 92 102 109 104 112
109 124 87 131 97 102 123 104 104 128
105 123 111 103 105 92 114 108 104 102
129 126 97 100 115 111 106 117 104 109
111 89 110 121 80 120 121 104 108 118
129 99 90 99 121 123 107 111 91 100
99 101 116 97 102 108 101 95 107 101
102 108 117 99 118 106 119 97 126 108
123 119 98 121 101 113 102 103 104 108
(1) 编制频率分布表;
(2) 绘制频率直方图;
(3) 估计该片经济林中底部周长小于 100 cm 的树木约占多少?底部周长不小于120cm的树木约占多少?
有了样本观测数据的频率分布,可以用它估计总体的取值规律.需要注意的是,由于样本的随机性,这种估计可能会存在一定误差,但这一误差一般不会影响对总体分布情况的大致了解.
某制造商为运动会生产一批直径为40 mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
40.02 40.00 39.98 40.00 39.99 40.00 39.98 40.01 39.98 39.99
40.00 39.99 39.95 40.01 40.02 39.98 40.00 39.99 40.00 39.96
(1) 完成下面的频率分布表,并在图中画出频率直方图和频率折线图;
分组 频数 频率
[39.95,39.97)
[39.97,39.99)
[39.99,40.01)
[40.01,40.03]
合计
(2) 假定乒乓球的直径误差不超过0.02 mm为合格品,若这批乒乓球的总数为 10 000 只,试根据抽样检查结果估计这批产品的合格只数.
1. 在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,该组直方图的高为h,则|a-b|的值等于( )
A. h·m B. C. D. 与m,h无关
2. (教材改编)如图为某企业员工年龄(岁)的频率直方图,从左到右依次为第一组、第二组、…、第五组,若第五组的员工有80人,则第二组的员工人数为( )
A. 140
B. 240
C. 280
D. 320
3. (多选)为组织好“市运会”,组委会征集了800名志愿者,现对他们的年龄进行抽样统计后,得到如图所示的频率直方图,但是年龄在[25,30)内的数据不慎丢失,则下列结论中正确的是( )
A. 年龄在[25,30)内对应小长方形的高度为0.04
B. 年龄在[25,30)内对应小长方形的高度为0.2
C. 这800名志愿者中年龄在[25,35)内的人数为400
D. 这800名志愿者中年龄在[25,35)内的人数为440
4. (教材改编)在样本的频率直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的 ,且样本容量为160,则中间一组的频数为________.
5. (2024江苏月考)有一组容量为50的样本,数据的分组及各组的数据如下:[10,15),4;[30,35),9;[15,20),5;[35,40),8;[20,25),10;[40,45],3;[25,30),11.
(1) 列出样本频率分布表;
(2) 画出频率直方图及频率折线图.
14.3.2 频率直方图
【活动方案】
思考:在频数直方图中,一般情况取相等的组距,其目的是使频数与相应的长方形面积成比例.如果组距不等,会给人以长方形的面积越大,频数越多的错觉.为了解决这个问题,让纵轴表示,这样每个矩形的面积恰好是该组的频率,这些矩形就构成了直方图,我们将这种直方图称为频率直方图.
1. 把横轴均分成若干段,每一段对应的长度称为组距,然后以此段为底作矩形,它的高等于该组的,这样得出一系列的矩形,每个矩形的面积恰好是该组的频率,这些矩形就构成了频率直方图.
2. ②
例1 ①根据频率分布表,作平面直角坐标系,以横轴表示身高,纵轴表示;
②在横轴上标上表示150.5,153.5,156.5,…,180.5的点(为方便起见,起始点150.5可适当前移);
③在上面标出的各点中,分别以连接相邻两点的线段为底做矩形,高等于该组的.
至此,就得到了这组数据的频率直方图,如下图所示.
频率折线图略.
跟踪训练 (1) 计算对应的频率,列出频率分布表,如下:
分组 频数 频率
[50,60) 2 0.04
[60,70) 6 0.12
[70,80) 10 0.20
[80,90) 20 0.40
[90,100] 12 0.24
合计 50 1.00
(2) 根据频率分布表,画出频率直方图及频率折线图,如下:
例2 (1) 从表中可以看出,这组数据的最大值为135,最小值为80,故全距为55,可将其分为11组,组距为5.从第1组[80,85)开始,将各组的频数、频率和填入下表:
分组 频数 频率
[80,85) 1 0.01 0.002
[85,90) 2 0.02 0.004
[90,95) 4 0.04 0.008
[95,100) 14 0.14 0.028
[100,105) 24 0.24 0.048
[105,110) 15 0.15 0.030
[110,115) 12 0.12 0.024
[115,120) 9 0.09 0.018
[120,125) 11 0.11 0.022
[125,130) 6 0.06 0.012
[130,135] 2 0.02 0.004
合计 100 1 0.2
(2) 这组数据的频率直方图如下图所示.
(3) 从频率分布表可以看出,该样本中小于100的频率为0.01+0.02+0.04+0.14=0.21,不小于120的频率为0.11+0.06+0.02=0.19,故可估计该片经济林中底部周长小于100 cm的树木约占21%,底部周长不小于120 cm的树木约占19%.
跟踪训练 (1) 频率分布表如下:
分组 频数 频率
[39.95,39.97) 2 0.10 5
[39.97,39.99) 4 0.20 10
[39.99,40.01) 10 0.50 25
[40.01,40.03] 4 0.20 10
合计 20 1.00 50
频率直方图、频率折线图如图所示.
(2) 因为抽样的20只产品中在[39.98,40.02]范围内的有18只,所以合格率为×100%=90%,所以根据抽样检查结果,可以估计这批产品的合格只数为9 000.
【检测反馈】
1. B 小长方形的高=,所以|a-b|==.
2. C 由题意,得5(a+0.06+0.04+0.02+0.01)=1,所以a=0.07.因为第五组的员工人数为80,所以第二组的员工人数为80×=280.
3. AD 年龄在[25,30)内对应小长方形的高度为×[1-(5×0.01+5×0.07+5×0.06+5×0.02)]=0.04,故A正确,B错误;年龄在[25,35)内的频率为0.04×5+0.07×5=0.55,故所求人数为0.55×800=440,故C错误,D正确.故选AD.
4. 32 设中间一个小长方形的面积为x,其他10个小长方形的面积之和为y,则有x+y=1,x=y,解得x=0.2,所以中间一组的频数为160×0.2=32.
5. (1) 由所给的数据,列出频率分布表如下:
分组 频数 频率
[10,15) 4 0.08
[15,20) 5 0.10
[20,25) 10 0.20
[25,30) 11 0.22
[30,35) 9 0.18
[35,40) 8 0.16
[40,45] 3 0.06
合计 50 1
(2) 频率直方图及频率折线图如图所示.
1. 能列出频率分布表,能画出频率直方图与频率折线图.
2. 学会用频率直方图研究数据的分布规律.
3. 能运用样本数据的频率直方图估计总体分布.
活动一 频率直方图与频率折线图的概念
思考
在频数直方图中,一般情况取相等的组距,其目的是什么?如果组距不等,会有什么影响?能否用其他的直方图来描述原来的数据?
1. 绘制频率直方图的一般步骤是什么?
2. 在频率直方图中,各个长方形的面积表示________.(填序号)
①落在相应各组的数据的频数;
②相应各组的频率;
③该样本所分成的组数;
④该样本的样本容量.
3. 将频率直方图中各个矩形的上底边的中点顺次连接起来,并将两边端点向外延伸半个组距,就得到频率折线图,简称折线图.
活动二 频率直方图与频率折线图的应用
例1 下表是100名学生身高(单位:cm)的频率分布表,根据数据画出频率直方图和频率折线图.
分组 频数累计 频数 频率
[150.5,153.5) 4 4 0.04
[153.5,156.5) 12 8 0.08
[156.5,159.5) 20 8 0.08
[159.5,162.5) 31 11 0.11
[162.5,165.5) 53 22 0.22
[165.5,168.5) 72 19 0.19
[168.5,171.5) 86 14 0.14
[171.5,174.5) 93 7 0.07
[174.5,177.5) 97 4 0.04
[177.5,180.5] 100 3 0.03
合计 100 1
频率直方图比频率分布表更直观、形象地反映了样本的分布规律.频率折线图的优点是它反映了数据的变化趋势.
在一次数学测验后,数学老师将某班全体学生(50人)的数学成绩进行初步统计后交给其班主任,数据如下表:
分数 [50,60) [60,70) [70,80) [80,90) [90,100]
人数 2 6 10 20 12
请你帮助这位班主任完成下面的统计分析工作.
(1) 列出频率分布表;
(2) 画出频率直方图及频率折线图.
例2 为了解一大片经济林的生长情况,随机测量其中的100株树木的底部周长,得到如下表所示的数据(单位:cm).
135 98 102 110 99 121 110 96 100 103
125 97 117 113 110 92 102 109 104 112
109 124 87 131 97 102 123 104 104 128
105 123 111 103 105 92 114 108 104 102
129 126 97 100 115 111 106 117 104 109
111 89 110 121 80 120 121 104 108 118
129 99 90 99 121 123 107 111 91 100
99 101 116 97 102 108 101 95 107 101
102 108 117 99 118 106 119 97 126 108
123 119 98 121 101 113 102 103 104 108
(1) 编制频率分布表;
(2) 绘制频率直方图;
(3) 估计该片经济林中底部周长小于 100 cm 的树木约占多少?底部周长不小于120cm的树木约占多少?
有了样本观测数据的频率分布,可以用它估计总体的取值规律.需要注意的是,由于样本的随机性,这种估计可能会存在一定误差,但这一误差一般不会影响对总体分布情况的大致了解.
某制造商为运动会生产一批直径为40 mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
40.02 40.00 39.98 40.00 39.99 40.00 39.98 40.01 39.98 39.99
40.00 39.99 39.95 40.01 40.02 39.98 40.00 39.99 40.00 39.96
(1) 完成下面的频率分布表,并在图中画出频率直方图和频率折线图;
分组 频数 频率
[39.95,39.97)
[39.97,39.99)
[39.99,40.01)
[40.01,40.03]
合计
(2) 假定乒乓球的直径误差不超过0.02 mm为合格品,若这批乒乓球的总数为 10 000 只,试根据抽样检查结果估计这批产品的合格只数.
1. 在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,该组直方图的高为h,则|a-b|的值等于( )
A. h·m B. C. D. 与m,h无关
2. (教材改编)如图为某企业员工年龄(岁)的频率直方图,从左到右依次为第一组、第二组、…、第五组,若第五组的员工有80人,则第二组的员工人数为( )
A. 140
B. 240
C. 280
D. 320
3. (多选)为组织好“市运会”,组委会征集了800名志愿者,现对他们的年龄进行抽样统计后,得到如图所示的频率直方图,但是年龄在[25,30)内的数据不慎丢失,则下列结论中正确的是( )
A. 年龄在[25,30)内对应小长方形的高度为0.04
B. 年龄在[25,30)内对应小长方形的高度为0.2
C. 这800名志愿者中年龄在[25,35)内的人数为400
D. 这800名志愿者中年龄在[25,35)内的人数为440
4. (教材改编)在样本的频率直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的 ,且样本容量为160,则中间一组的频数为________.
5. (2024江苏月考)有一组容量为50的样本,数据的分组及各组的数据如下:[10,15),4;[30,35),9;[15,20),5;[35,40),8;[20,25),10;[40,45],3;[25,30),11.
(1) 列出样本频率分布表;
(2) 画出频率直方图及频率折线图.
14.3.2 频率直方图
【活动方案】
思考:在频数直方图中,一般情况取相等的组距,其目的是使频数与相应的长方形面积成比例.如果组距不等,会给人以长方形的面积越大,频数越多的错觉.为了解决这个问题,让纵轴表示,这样每个矩形的面积恰好是该组的频率,这些矩形就构成了直方图,我们将这种直方图称为频率直方图.
1. 把横轴均分成若干段,每一段对应的长度称为组距,然后以此段为底作矩形,它的高等于该组的,这样得出一系列的矩形,每个矩形的面积恰好是该组的频率,这些矩形就构成了频率直方图.
2. ②
例1 ①根据频率分布表,作平面直角坐标系,以横轴表示身高,纵轴表示;
②在横轴上标上表示150.5,153.5,156.5,…,180.5的点(为方便起见,起始点150.5可适当前移);
③在上面标出的各点中,分别以连接相邻两点的线段为底做矩形,高等于该组的.
至此,就得到了这组数据的频率直方图,如下图所示.
频率折线图略.
跟踪训练 (1) 计算对应的频率,列出频率分布表,如下:
分组 频数 频率
[50,60) 2 0.04
[60,70) 6 0.12
[70,80) 10 0.20
[80,90) 20 0.40
[90,100] 12 0.24
合计 50 1.00
(2) 根据频率分布表,画出频率直方图及频率折线图,如下:
例2 (1) 从表中可以看出,这组数据的最大值为135,最小值为80,故全距为55,可将其分为11组,组距为5.从第1组[80,85)开始,将各组的频数、频率和填入下表:
分组 频数 频率
[80,85) 1 0.01 0.002
[85,90) 2 0.02 0.004
[90,95) 4 0.04 0.008
[95,100) 14 0.14 0.028
[100,105) 24 0.24 0.048
[105,110) 15 0.15 0.030
[110,115) 12 0.12 0.024
[115,120) 9 0.09 0.018
[120,125) 11 0.11 0.022
[125,130) 6 0.06 0.012
[130,135] 2 0.02 0.004
合计 100 1 0.2
(2) 这组数据的频率直方图如下图所示.
(3) 从频率分布表可以看出,该样本中小于100的频率为0.01+0.02+0.04+0.14=0.21,不小于120的频率为0.11+0.06+0.02=0.19,故可估计该片经济林中底部周长小于100 cm的树木约占21%,底部周长不小于120 cm的树木约占19%.
跟踪训练 (1) 频率分布表如下:
分组 频数 频率
[39.95,39.97) 2 0.10 5
[39.97,39.99) 4 0.20 10
[39.99,40.01) 10 0.50 25
[40.01,40.03] 4 0.20 10
合计 20 1.00 50
频率直方图、频率折线图如图所示.
(2) 因为抽样的20只产品中在[39.98,40.02]范围内的有18只,所以合格率为×100%=90%,所以根据抽样检查结果,可以估计这批产品的合格只数为9 000.
【检测反馈】
1. B 小长方形的高=,所以|a-b|==.
2. C 由题意,得5(a+0.06+0.04+0.02+0.01)=1,所以a=0.07.因为第五组的员工人数为80,所以第二组的员工人数为80×=280.
3. AD 年龄在[25,30)内对应小长方形的高度为×[1-(5×0.01+5×0.07+5×0.06+5×0.02)]=0.04,故A正确,B错误;年龄在[25,35)内的频率为0.04×5+0.07×5=0.55,故所求人数为0.55×800=440,故C错误,D正确.故选AD.
4. 32 设中间一个小长方形的面积为x,其他10个小长方形的面积之和为y,则有x+y=1,x=y,解得x=0.2,所以中间一组的频数为160×0.2=32.
5. (1) 由所给的数据,列出频率分布表如下:
分组 频数 频率
[10,15) 4 0.08
[15,20) 5 0.10
[20,25) 10 0.20
[25,30) 11 0.22
[30,35) 9 0.18
[35,40) 8 0.16
[40,45] 3 0.06
合计 50 1
(2) 频率直方图及频率折线图如图所示.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
