23.3.4 相似三角形的应用 练习(含答案)初中数学华东师大版九年级上册
文档属性
| 名称 | 23.3.4 相似三角形的应用 练习(含答案)初中数学华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:23:02 | ||
图片预览


文档简介
第23章 图形的相似
23.3 相似三角形
4.相似三角形的应用
1.测量物体的高度
原 理:测量顶部无法到达的物体的高度,通常利用构造相似三角形解决.
方 法:(1)利用阳光下的影子;
(2)利用标杆;
(3)利用镜子的反射.
2.测量河宽
方 法:构造相似三角形.
类型之一 利用相似测量物体的高度
某校某班综合实践活动课上,同学们开展了测量本校旗杆高度的实践活动.如图,他们在旗杆底部所在的平地上放置一个平面镜E来测量学校旗杆AB的高度,镜子中心E与旗杆的距离EB=20m.当镜子中心E与测量者的距离DE=2m时,测量者刚好从镜子中看到旗杆顶部的端点A.已知测量者的身高为1.6m,测量者的眼睛距地面的高度为1.5m.
(1)在计算过程中,C、D之间的距离应是 m;
(2)根据以上测量结果,求出学校旗杆AB的高度.
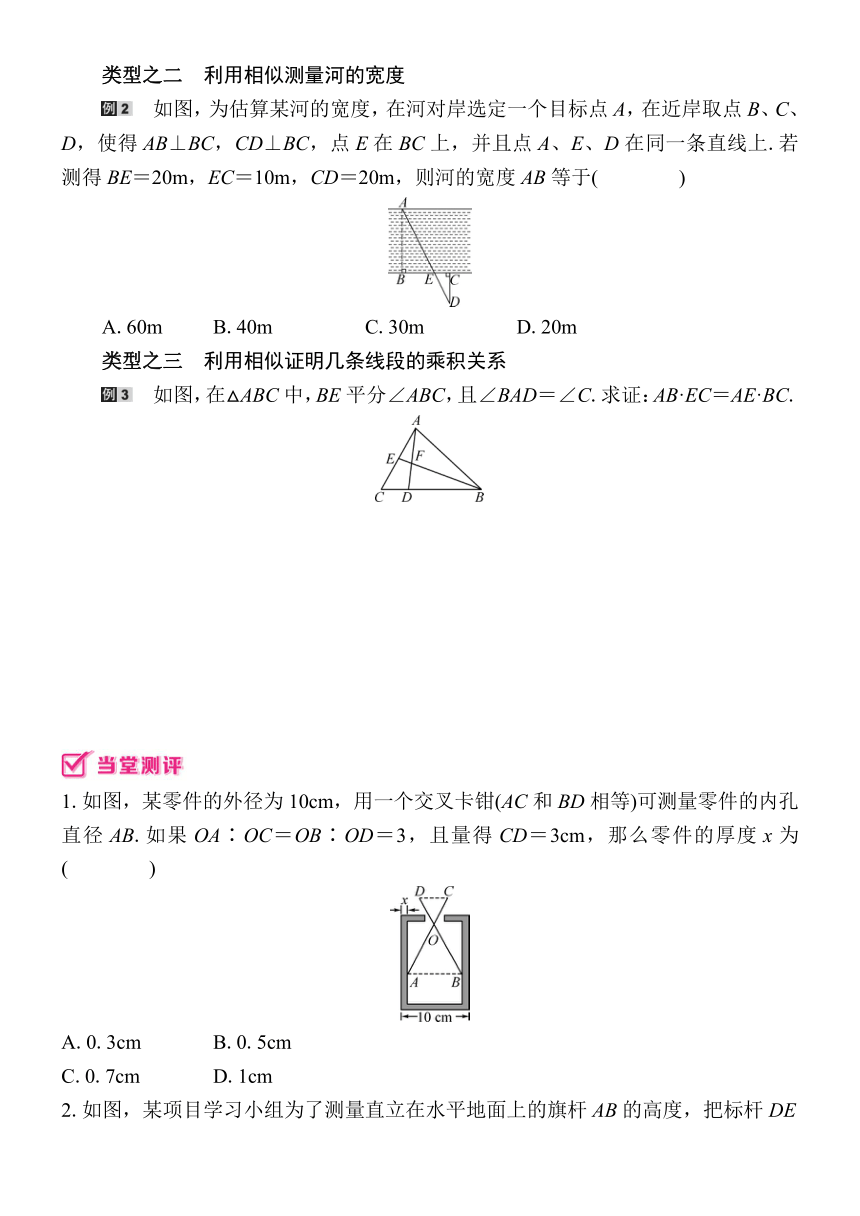
类型之二 利用相似测量河的宽度
如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B、C、D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A、E、D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
类型之三 利用相似证明几条线段的乘积关系
如图,在△ABC中,BE平分∠ABC,且∠BAD=∠C.求证:AB·EC=AE·BC.
1.如图,某零件的外径为10cm,用一个交叉卡钳(AC和BD相等)可测量零件的内孔直径AB.如果OA∶OC=OB∶OD=3,且量得CD=3cm,那么零件的厚度x为( )
A.0.3cm B.0.5cm
C.0.7cm D.1cm
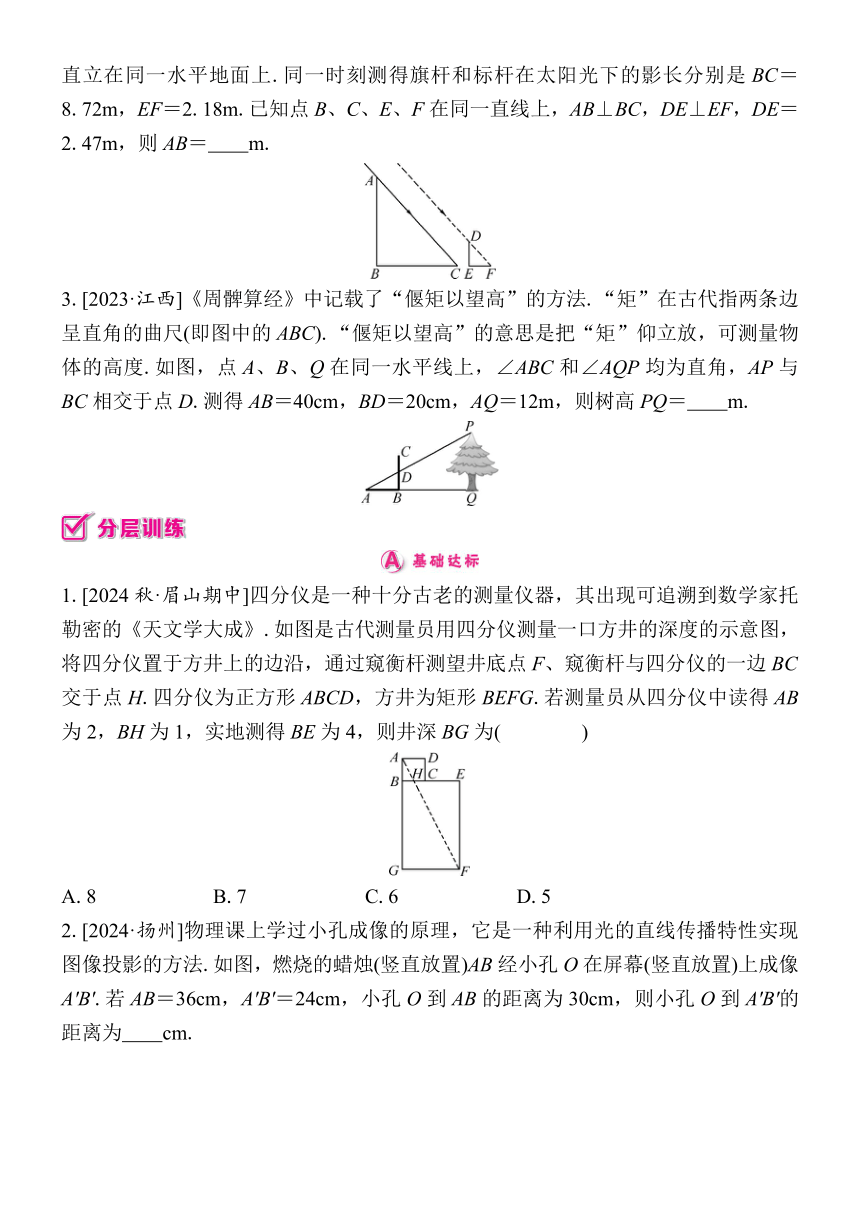
2.如图,某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上.同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知点B、C、E、F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB= m.
3.[2023·江西]《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A、B、Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=12m,则树高PQ= m.
1.[2024秋·眉山期中]四分仪是一种十分古老的测量仪器,其出现可追溯到数学家托勒密的《天文学大成》.如图是古代测量员用四分仪测量一口方井的深度的示意图,将四分仪置于方井上的边沿,通过窥衡杆测望井底点F、窥衡杆与四分仪的一边BC交于点H.四分仪为正方形ABCD,方井为矩形BEFG.若测量员从四分仪中读得AB为2,BH为1,实地测得BE为4,则井深BG为( )
A.8 B.7 C.6 D.5
2.[2024·扬州]物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A'B'.若AB=36cm,A'B'=24cm,小孔O到AB的距离为30cm,则小孔O到A'B'的距离为 cm.
3.[2024秋·福建漳州期中]小明准备送礼物给妈妈,他利用边长为5dm的正方形纸板按如图所示裁剪,制作一个正方体礼品盒,则这个礼品盒的体积为 dm3.
4.某数学兴趣小组想测量一棵树的高度,如图,在阳光下,一名同学测得一根长1m的竹竿的影长为0.8m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部影子落在教学楼的墙壁上,其墙壁上影长为3m,落在地面上的影长为4m,则树高为 m.
5.[2024秋·东坡区期中]小亮和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度,检验自己掌握知识和运用知识的能力.如图,在阳光下,小亮站在水平地面的D处,此时小亮的影子顶端与旗杆的影子顶端E重合,这时小亮的影长DE=1m.一段时间后,小亮从D点沿BD方向走了2.6m到达G处,此时小亮的影子顶端与旗杆的影子顶端H重合,这时小亮的影长GH=1.4m.已知小亮的身高CD=FG=1.6m,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH.请你根据题中提供的相关信息,求出旗杆的高度.
6.为了加强视力保护意识,欢欢想在书房里挂一张测试距离为5m的视力表,但两面墙的距离只有3m.在一次课题学习课上,欢欢向全班同学征集“如何解决空间过小无法放置视力表问题”的方案,其中甲、乙两位同学的设计方案新颖,构思巧妙.
甲 乙
图例
甲 乙
方案 图中①是测试距离为5m的大视力表,可以用硬纸板制作一个测试距离为3m的小视力表②.通过测量大视力表中“E”的高度(BC的长),即可求出小视力表中相应的“E”的高度(DF的长). 使用平面镜成像的原理来解决房间小的问题.如图,在相距3m的两面墙上分别悬挂视力表(AB)与平面镜(MN),由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表AB的上、下边沿A、B发出的光线经平面镜MN的上下边沿反射后射入人眼C处,通过测量视力表的全长(AB)就可以计算出镜长MN.
(1)如果甲同学的方案中大视力表中“E”的高是3.5cm,那么小视力表中相应“E”的高是多少?
(2)如果乙同学的方案中视力表的全长为0.8m,请计算出镜长至少为多少米?
7.(创新意识、应用观念)[2024·自贡]为测量水平操场上旗杆的高度,某班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m.
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m,求旗杆高度.
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具、优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了某广场一个雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M、N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在该广场上点E处,同学们用注水管确定与雕塑底部B处于同一水平线的D、G两点,并标记观测视线DA与标高线的交点C,测得CG=1.8m,DG=1.5m.将观测点D后移24m到D'处,采用同样的方法,测得C'G'=1.2m,D'G'=2m.求雕塑的高度(结果精确到1m).
参考答案
【归类探究】
【例1】(1)1.5 (2)学校旗杆AB的高度是15m.
【例2】B
【例3】略
【当堂测评】
1.B 2.9.88 3.6
【分层训练】
1.C 2.20 3.8 4.8
5.旗杆的高度为12m.
6.(1)小视力表中相应“E”的高是2.1cm.
(2)镜长至少为0.32m.
7.(1)11.3 (2)旗杆高度为12m.
(3)雕塑高度AB约为29m.
。
23.3 相似三角形
4.相似三角形的应用
1.测量物体的高度
原 理:测量顶部无法到达的物体的高度,通常利用构造相似三角形解决.
方 法:(1)利用阳光下的影子;
(2)利用标杆;
(3)利用镜子的反射.
2.测量河宽
方 法:构造相似三角形.
类型之一 利用相似测量物体的高度
某校某班综合实践活动课上,同学们开展了测量本校旗杆高度的实践活动.如图,他们在旗杆底部所在的平地上放置一个平面镜E来测量学校旗杆AB的高度,镜子中心E与旗杆的距离EB=20m.当镜子中心E与测量者的距离DE=2m时,测量者刚好从镜子中看到旗杆顶部的端点A.已知测量者的身高为1.6m,测量者的眼睛距地面的高度为1.5m.
(1)在计算过程中,C、D之间的距离应是 m;
(2)根据以上测量结果,求出学校旗杆AB的高度.
类型之二 利用相似测量河的宽度
如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B、C、D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A、E、D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
类型之三 利用相似证明几条线段的乘积关系
如图,在△ABC中,BE平分∠ABC,且∠BAD=∠C.求证:AB·EC=AE·BC.
1.如图,某零件的外径为10cm,用一个交叉卡钳(AC和BD相等)可测量零件的内孔直径AB.如果OA∶OC=OB∶OD=3,且量得CD=3cm,那么零件的厚度x为( )
A.0.3cm B.0.5cm
C.0.7cm D.1cm
2.如图,某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上.同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知点B、C、E、F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB= m.
3.[2023·江西]《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A、B、Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=12m,则树高PQ= m.
1.[2024秋·眉山期中]四分仪是一种十分古老的测量仪器,其出现可追溯到数学家托勒密的《天文学大成》.如图是古代测量员用四分仪测量一口方井的深度的示意图,将四分仪置于方井上的边沿,通过窥衡杆测望井底点F、窥衡杆与四分仪的一边BC交于点H.四分仪为正方形ABCD,方井为矩形BEFG.若测量员从四分仪中读得AB为2,BH为1,实地测得BE为4,则井深BG为( )
A.8 B.7 C.6 D.5
2.[2024·扬州]物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A'B'.若AB=36cm,A'B'=24cm,小孔O到AB的距离为30cm,则小孔O到A'B'的距离为 cm.
3.[2024秋·福建漳州期中]小明准备送礼物给妈妈,他利用边长为5dm的正方形纸板按如图所示裁剪,制作一个正方体礼品盒,则这个礼品盒的体积为 dm3.
4.某数学兴趣小组想测量一棵树的高度,如图,在阳光下,一名同学测得一根长1m的竹竿的影长为0.8m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部影子落在教学楼的墙壁上,其墙壁上影长为3m,落在地面上的影长为4m,则树高为 m.
5.[2024秋·东坡区期中]小亮和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度,检验自己掌握知识和运用知识的能力.如图,在阳光下,小亮站在水平地面的D处,此时小亮的影子顶端与旗杆的影子顶端E重合,这时小亮的影长DE=1m.一段时间后,小亮从D点沿BD方向走了2.6m到达G处,此时小亮的影子顶端与旗杆的影子顶端H重合,这时小亮的影长GH=1.4m.已知小亮的身高CD=FG=1.6m,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH.请你根据题中提供的相关信息,求出旗杆的高度.
6.为了加强视力保护意识,欢欢想在书房里挂一张测试距离为5m的视力表,但两面墙的距离只有3m.在一次课题学习课上,欢欢向全班同学征集“如何解决空间过小无法放置视力表问题”的方案,其中甲、乙两位同学的设计方案新颖,构思巧妙.
甲 乙
图例
甲 乙
方案 图中①是测试距离为5m的大视力表,可以用硬纸板制作一个测试距离为3m的小视力表②.通过测量大视力表中“E”的高度(BC的长),即可求出小视力表中相应的“E”的高度(DF的长). 使用平面镜成像的原理来解决房间小的问题.如图,在相距3m的两面墙上分别悬挂视力表(AB)与平面镜(MN),由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表AB的上、下边沿A、B发出的光线经平面镜MN的上下边沿反射后射入人眼C处,通过测量视力表的全长(AB)就可以计算出镜长MN.
(1)如果甲同学的方案中大视力表中“E”的高是3.5cm,那么小视力表中相应“E”的高是多少?
(2)如果乙同学的方案中视力表的全长为0.8m,请计算出镜长至少为多少米?
7.(创新意识、应用观念)[2024·自贡]为测量水平操场上旗杆的高度,某班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m.
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m,求旗杆高度.
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具、优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了某广场一个雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M、N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在该广场上点E处,同学们用注水管确定与雕塑底部B处于同一水平线的D、G两点,并标记观测视线DA与标高线的交点C,测得CG=1.8m,DG=1.5m.将观测点D后移24m到D'处,采用同样的方法,测得C'G'=1.2m,D'G'=2m.求雕塑的高度(结果精确到1m).
参考答案
【归类探究】
【例1】(1)1.5 (2)学校旗杆AB的高度是15m.
【例2】B
【例3】略
【当堂测评】
1.B 2.9.88 3.6
【分层训练】
1.C 2.20 3.8 4.8
5.旗杆的高度为12m.
6.(1)小视力表中相应“E”的高是2.1cm.
(2)镜长至少为0.32m.
7.(1)11.3 (2)旗杆高度为12m.
(3)雕塑高度AB约为29m.
。
