23.4 中位线 练习(含答案)初中数学华东师大版九年级上册
文档属性
| 名称 | 23.4 中位线 练习(含答案)初中数学华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 417.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:23:34 | ||
图片预览


文档简介
第23章 图形的相似
23.4 中位线
1.三角形的中位线
三角形的中位线:连结三角形两边中点的线段叫做 .
2.中位线的性质
定 理:三角形的中位线 ,并且 .
3.三角形的重心
定 义:三角形三条边上的 交于一点,这个点就是三角形的重心.
性 质:重心与一边中点的连线长是对应中线长的.
类型之一 三角形中位线定理的证明
试证明三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:先画出图形,再根据图形写出已知、求证和证明过程)
类型之二 利用三角形的中位线定理证明中点四边形
[2023秋·临川区期中]如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点,则四边形EHFG是 .
类型之三 三角形中位线的综合运用
如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.
(1)如图1,BE的延长线与边AC相交于点D,求证:EF=(AC-AB);
(2)如图2,写出线段AB、AC、EF之间的数量关系,并证明你的结论.
1.如图,点M、N分别是△ABC的边AB、AC的中点.若∠A=65°,∠ANM=45°,则∠B的度数为( )
A.20° B.45° C.65° D.70°
2.[2023·金华]如图,把两根钢条OA、OB的一个端点连在一起,点C、D分别是OA、OB的中点.若CD=4cm,则该工件内槽宽AB的长为 cm.
3.如图,在△ABC中,D、E分别是边AB、AC的中点,F、G分别是AD、AE的中点,且FG=2 cm,则BC的长是 cm.
4.如图,在△ABC中,D、E、F分别是边AB、BC、CA的中点.若△DEF的周长为10,则△ABC的周长为 .
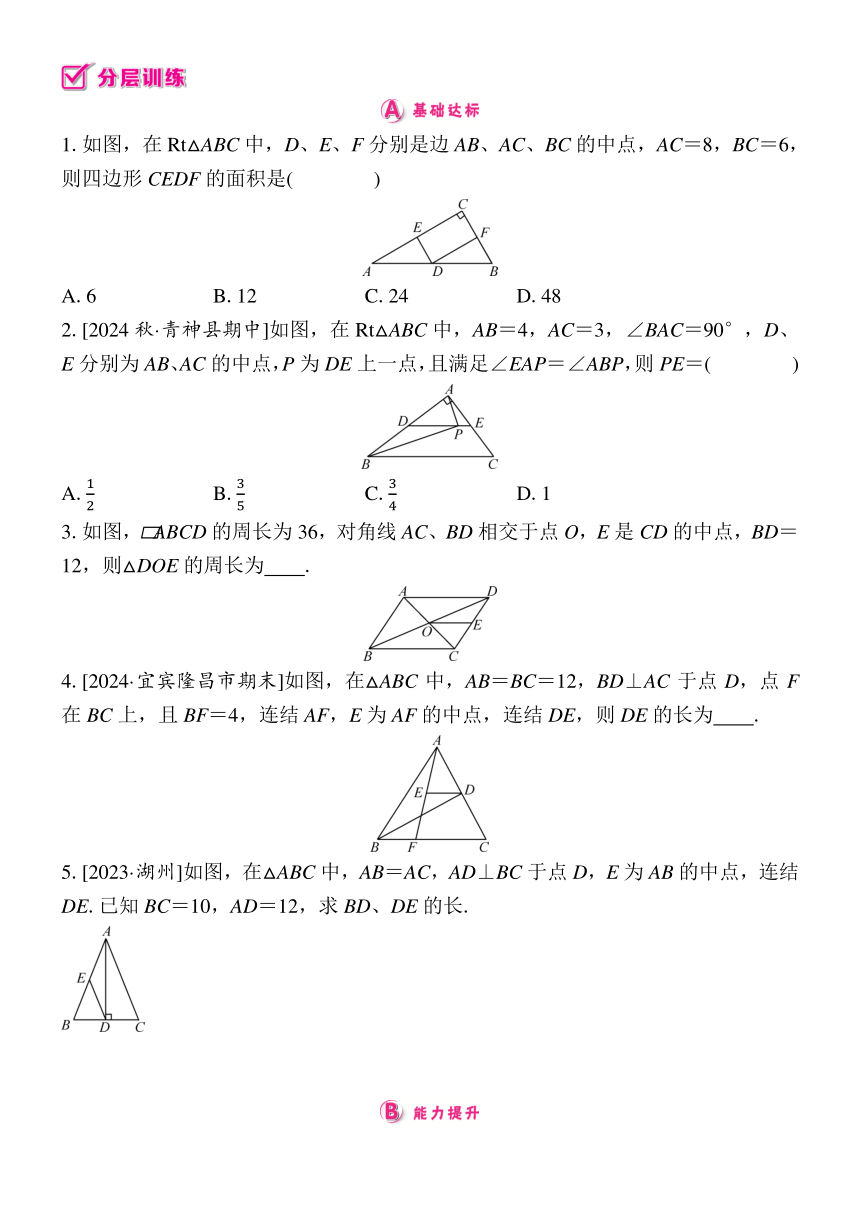
1.如图,在Rt△ABC中,D、E、F分别是边AB、AC、BC的中点,AC=8,BC=6,则四边形CEDF的面积是( )
A.6 B.12 C.24 D.48
2.[2024秋·青神县期中]如图,在Rt△ABC中,AB=4,AC=3,∠BAC=90°,D、E分别为AB、AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
3.如图, ABCD的周长为36,对角线AC、BD相交于点O,E是CD的中点,BD=12,则△DOE的周长为 .
4.[2024·宜宾隆昌市期末]如图,在△ABC中,AB=BC=12,BD⊥AC于点D,点F在BC上,且BF=4,连结AF,E为AF的中点,连结DE,则DE的长为 .
5.[2023·湖州]如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AB的中点,连结DE.已知BC=10,AD=12,求BD、DE的长.
6.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数为 .
7.如图,△ABC的中线BE、CF相交于点G,连结EF.求证:BG=2GE,CG=2GF.
8.如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过点A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC).
9.[2024·凉州区二模]如图,在四边形ABCD中,AC=BD,AC、BD交于点O,E、F分别是AB、CD中点,EF分别交AC、BD于点H、G.求证:OG=OH.
10.(模型观念)[2023·山西]阅读与思考.
下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.
瓦里尼翁平行四边形.
我们知道,如图1,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连结E、F、G、H,得到的四边形EFGH是平行四边形.
图1
我查阅了许多资料,得知这个平行四边形EFGH被称为瓦里尼翁平行四边形.瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.此结论证明如下:
证明:如图2,连结AC,分别交EH、FG于点P、Q,过点D作DM⊥AC于点M,交HG于点N.
图2
∵H、G分别为AD、CD的中点,
∴HG∥AC,HG=AC,(依据1)
∴=.
∵DG=GC,∴DN=NM=DM.
∵四边形EFGH是瓦里尼翁平行四边形,∴HE∥GF,即HP∥GQ.
∵HG∥AC,即HG∥PQ,
∴四边形HPQG是平行四边形,(依据2)∴S HPQG=HG·MN=HG·DM.
∵S△ADC=AC·DM=HG·DM,
∴S HPQG=S△ADC.同理,……
任务:
(1)材料中的依据1是指: ;
依据2是指: .
(2)请用刻度尺、三角板等工具,画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH,使得四边形EFGH为矩形.(要求同时画出四边形ABCD的对角线)
(3)在图1中,分别连结AC、BD得到图3,请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC、BD长度的关系,并证明你的结论.
图3
参考答案
【预习导航】
1.三角形的中位线 2.平行于第三边 等于第三边的一半 3.中线
【归类探究】
【例1】略
【例2】菱形
【例3】(1)略
(2)EF=(AB-AC).证明略.
【当堂测评】
1.D 2.8 3.8 4.20
【分层训练】
1.B 2.A 3.15 4.4
5.BD=5,DE=
6.40° 7.略 8.略 9.略
10.(1)三角形的中位线定理 两组对边分别平行的四边形是平行四边形
(2)略
(3)瓦里尼翁平行四边形EFGH的周长等于AC+BD.理由略.
。
23.4 中位线
1.三角形的中位线
三角形的中位线:连结三角形两边中点的线段叫做 .
2.中位线的性质
定 理:三角形的中位线 ,并且 .
3.三角形的重心
定 义:三角形三条边上的 交于一点,这个点就是三角形的重心.
性 质:重心与一边中点的连线长是对应中线长的.
类型之一 三角形中位线定理的证明
试证明三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:先画出图形,再根据图形写出已知、求证和证明过程)
类型之二 利用三角形的中位线定理证明中点四边形
[2023秋·临川区期中]如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点,则四边形EHFG是 .
类型之三 三角形中位线的综合运用
如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是BC的中点.
(1)如图1,BE的延长线与边AC相交于点D,求证:EF=(AC-AB);
(2)如图2,写出线段AB、AC、EF之间的数量关系,并证明你的结论.
1.如图,点M、N分别是△ABC的边AB、AC的中点.若∠A=65°,∠ANM=45°,则∠B的度数为( )
A.20° B.45° C.65° D.70°
2.[2023·金华]如图,把两根钢条OA、OB的一个端点连在一起,点C、D分别是OA、OB的中点.若CD=4cm,则该工件内槽宽AB的长为 cm.
3.如图,在△ABC中,D、E分别是边AB、AC的中点,F、G分别是AD、AE的中点,且FG=2 cm,则BC的长是 cm.
4.如图,在△ABC中,D、E、F分别是边AB、BC、CA的中点.若△DEF的周长为10,则△ABC的周长为 .
1.如图,在Rt△ABC中,D、E、F分别是边AB、AC、BC的中点,AC=8,BC=6,则四边形CEDF的面积是( )
A.6 B.12 C.24 D.48
2.[2024秋·青神县期中]如图,在Rt△ABC中,AB=4,AC=3,∠BAC=90°,D、E分别为AB、AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
3.如图, ABCD的周长为36,对角线AC、BD相交于点O,E是CD的中点,BD=12,则△DOE的周长为 .
4.[2024·宜宾隆昌市期末]如图,在△ABC中,AB=BC=12,BD⊥AC于点D,点F在BC上,且BF=4,连结AF,E为AF的中点,连结DE,则DE的长为 .
5.[2023·湖州]如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AB的中点,连结DE.已知BC=10,AD=12,求BD、DE的长.
6.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数为 .
7.如图,△ABC的中线BE、CF相交于点G,连结EF.求证:BG=2GE,CG=2GF.
8.如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过点A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC).
9.[2024·凉州区二模]如图,在四边形ABCD中,AC=BD,AC、BD交于点O,E、F分别是AB、CD中点,EF分别交AC、BD于点H、G.求证:OG=OH.
10.(模型观念)[2023·山西]阅读与思考.
下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.
瓦里尼翁平行四边形.
我们知道,如图1,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连结E、F、G、H,得到的四边形EFGH是平行四边形.
图1
我查阅了许多资料,得知这个平行四边形EFGH被称为瓦里尼翁平行四边形.瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.此结论证明如下:
证明:如图2,连结AC,分别交EH、FG于点P、Q,过点D作DM⊥AC于点M,交HG于点N.
图2
∵H、G分别为AD、CD的中点,
∴HG∥AC,HG=AC,(依据1)
∴=.
∵DG=GC,∴DN=NM=DM.
∵四边形EFGH是瓦里尼翁平行四边形,∴HE∥GF,即HP∥GQ.
∵HG∥AC,即HG∥PQ,
∴四边形HPQG是平行四边形,(依据2)∴S HPQG=HG·MN=HG·DM.
∵S△ADC=AC·DM=HG·DM,
∴S HPQG=S△ADC.同理,……
任务:
(1)材料中的依据1是指: ;
依据2是指: .
(2)请用刻度尺、三角板等工具,画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH,使得四边形EFGH为矩形.(要求同时画出四边形ABCD的对角线)
(3)在图1中,分别连结AC、BD得到图3,请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC、BD长度的关系,并证明你的结论.
图3
参考答案
【预习导航】
1.三角形的中位线 2.平行于第三边 等于第三边的一半 3.中线
【归类探究】
【例1】略
【例2】菱形
【例3】(1)略
(2)EF=(AB-AC).证明略.
【当堂测评】
1.D 2.8 3.8 4.20
【分层训练】
1.B 2.A 3.15 4.4
5.BD=5,DE=
6.40° 7.略 8.略 9.略
10.(1)三角形的中位线定理 两组对边分别平行的四边形是平行四边形
(2)略
(3)瓦里尼翁平行四边形EFGH的周长等于AC+BD.理由略.
。
