24.1 测量 练习(含答案) 初中数学华东师大版九年级上册
文档属性
| 名称 | 24.1 测量 练习(含答案) 初中数学华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 461.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览

文档简介
第24章 解直角三角形
24.1 测量
1.利用直角三角形中的边角关系解决实际问题
方 法:利用特殊的直角三角形来解决一些实际问题.
2.利用相似三角形知识进行物体高度的测量与计算
方 法:在实际测量物体高度、宽度时,关键是要构造和实物相似的三角形,而且要能测量已知三角形的各条线段的长,运用相似三角形的知识求解.
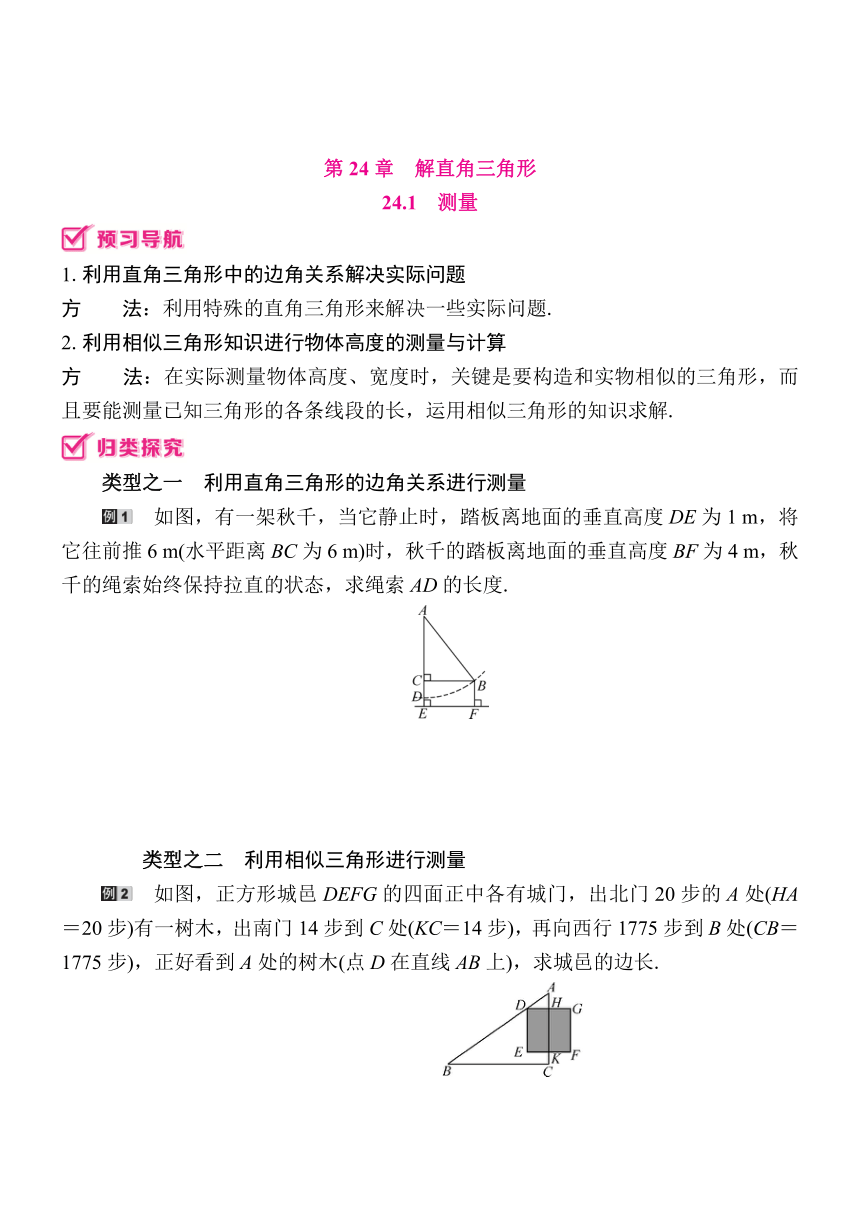
类型之一 利用直角三角形的边角关系进行测量
如图,有一架秋千,当它静止时,踏板离地面的垂直高度DE为1 m,将它往前推6 m(水平距离BC为6 m)时,秋千的踏板离地面的垂直高度BF为4 m,秋千的绳索始终保持拉直的状态,求绳索AD的长度.
类型之二 利用相似三角形进行测量
如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,出南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),求城邑的边长.
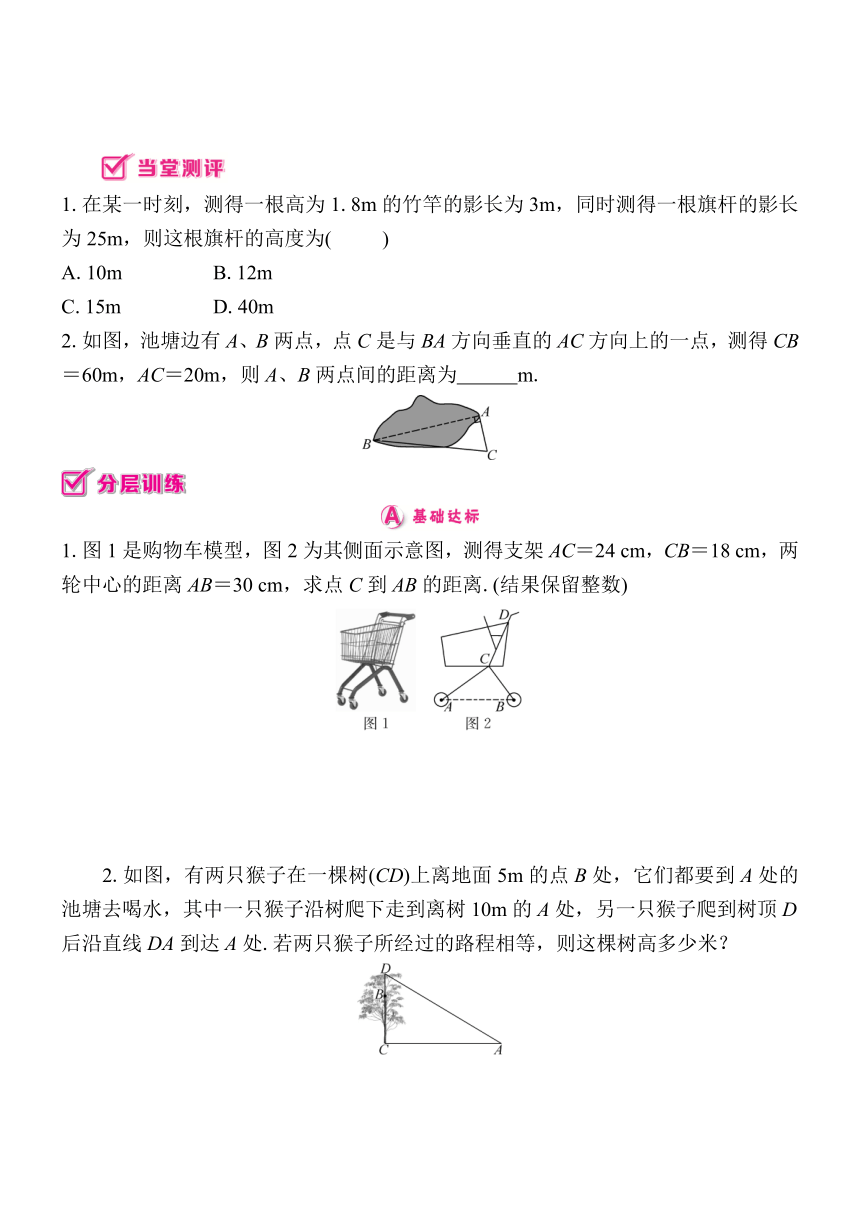
1.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,则这根旗杆的高度为( )
A.10m B.12m
C.15m D.40m
2.如图,池塘边有A、B两点,点C是与BA方向垂直的AC方向上的一点,测得CB=60m,AC=20m,则A、B两点间的距离为 m.
1.图1是购物车模型,图2为其侧面示意图,测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,求点C到AB的距离.(结果保留整数)
2.如图,有两只猴子在一棵树(CD)上离地面5m的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树10m的A处,另一只猴子爬到树顶D后沿直线DA到达A处.若两只猴子所经过的路程相等,则这棵树高多少米?
3.为测量操场上旗杆的高度,设计的测量方案如图所示.标杆高度CD为3m,标杆与旗杆的水平距离BD为15m,人的眼睛与地面的高度EF为1.6m,人与标杆CD的水平距离DF为2m,E、C、A三点共线,求旗杆AB的高度.
4.(模型观念)如图,王华同学在晚上从路灯电杆AC走向路灯电杆BD,当他走到点P时,发现他身后的影子的顶端刚好接触到AC的底部,当他再向前步行12m到达点Q时,发现他身前的影子的顶端刚好接触到BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯电杆BD处时,他在路灯C下的影长是多少?
参考答案
【归类探究】
【例1】绳索AD的长度是7.5 m.
【例2】城邑的边长为250步.
【当堂测评】
1.C 2.40
【分层训练】
1.点C到AB的距离约为14 cm.
2.这棵树高7.5m.
3.旗杆AB的高度为13.5m.
4.(1)两个路灯之间的距离为18m.
(2)他在路灯C下的影长为3.6m.
。
24.1 测量
1.利用直角三角形中的边角关系解决实际问题
方 法:利用特殊的直角三角形来解决一些实际问题.
2.利用相似三角形知识进行物体高度的测量与计算
方 法:在实际测量物体高度、宽度时,关键是要构造和实物相似的三角形,而且要能测量已知三角形的各条线段的长,运用相似三角形的知识求解.
类型之一 利用直角三角形的边角关系进行测量
如图,有一架秋千,当它静止时,踏板离地面的垂直高度DE为1 m,将它往前推6 m(水平距离BC为6 m)时,秋千的踏板离地面的垂直高度BF为4 m,秋千的绳索始终保持拉直的状态,求绳索AD的长度.
类型之二 利用相似三角形进行测量
如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,出南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),求城邑的边长.
1.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,则这根旗杆的高度为( )
A.10m B.12m
C.15m D.40m
2.如图,池塘边有A、B两点,点C是与BA方向垂直的AC方向上的一点,测得CB=60m,AC=20m,则A、B两点间的距离为 m.
1.图1是购物车模型,图2为其侧面示意图,测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,求点C到AB的距离.(结果保留整数)
2.如图,有两只猴子在一棵树(CD)上离地面5m的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树10m的A处,另一只猴子爬到树顶D后沿直线DA到达A处.若两只猴子所经过的路程相等,则这棵树高多少米?
3.为测量操场上旗杆的高度,设计的测量方案如图所示.标杆高度CD为3m,标杆与旗杆的水平距离BD为15m,人的眼睛与地面的高度EF为1.6m,人与标杆CD的水平距离DF为2m,E、C、A三点共线,求旗杆AB的高度.
4.(模型观念)如图,王华同学在晚上从路灯电杆AC走向路灯电杆BD,当他走到点P时,发现他身后的影子的顶端刚好接触到AC的底部,当他再向前步行12m到达点Q时,发现他身前的影子的顶端刚好接触到BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯电杆BD处时,他在路灯C下的影长是多少?
参考答案
【归类探究】
【例1】绳索AD的长度是7.5 m.
【例2】城邑的边长为250步.
【当堂测评】
1.C 2.40
【分层训练】
1.点C到AB的距离约为14 cm.
2.这棵树高7.5m.
3.旗杆AB的高度为13.5m.
4.(1)两个路灯之间的距离为18m.
(2)他在路灯C下的影长为3.6m.
。
