24.2 直角三角形的性质 练习(含答案) 初中数学华东师大版九年级上册
文档属性
| 名称 | 24.2 直角三角形的性质 练习(含答案) 初中数学华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:29:54 | ||
图片预览

文档简介
第24章 解直角三角形
24.2 直角三角形的性质
1.直角三角形的性质
锐角关系:直角三角形的两个锐角 .
勾股定理:直角三角形两直角边的平方和等于 .
2.直角三角形斜边上的中线
性 质:直角三角形斜边上的中线等于 .
3.含30°角的直角三角形的性质
性 质:在直角三角形中,30°角所对的直角边等于斜边的一半.
类型之一 直角三角形斜边上的中线的性质
[2024·江都区期末]如图,在锐角三角形ABC中,CD、BE分别是边AB、AC上的高,点M、N分别是线段DE、BC的中点.
(1)求证:MN⊥DE;
(2)连结DN、EN,猜想∠A与∠DNE之间的关系,并说明理由.
类型之二 含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.试作出图形,写出已知、求证,并给出证明.
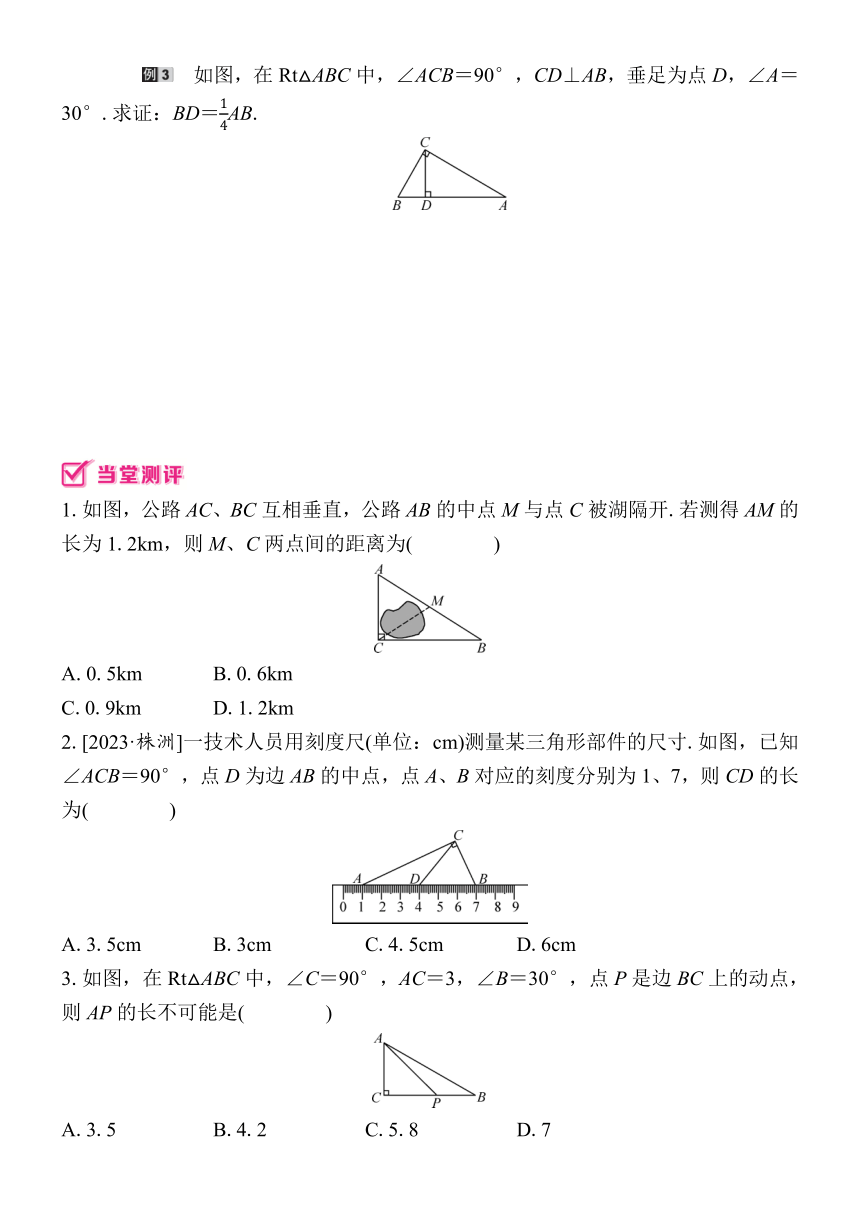
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠A=30°.求证:BD=AB.
1.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M、C两点间的距离为( )
A.0.5km B.0.6km
C.0.9km D.1.2km
2.[2023·株洲]一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB=90°,点D为边AB的中点,点A、B对应的刻度分别为1、7,则CD的长为( )
A.3.5cm B.3cm C.4.5cm D.6cm
3.如图,在Rt△ABC中,∠C=90°,AC=3,∠B=30°,点P是边BC上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
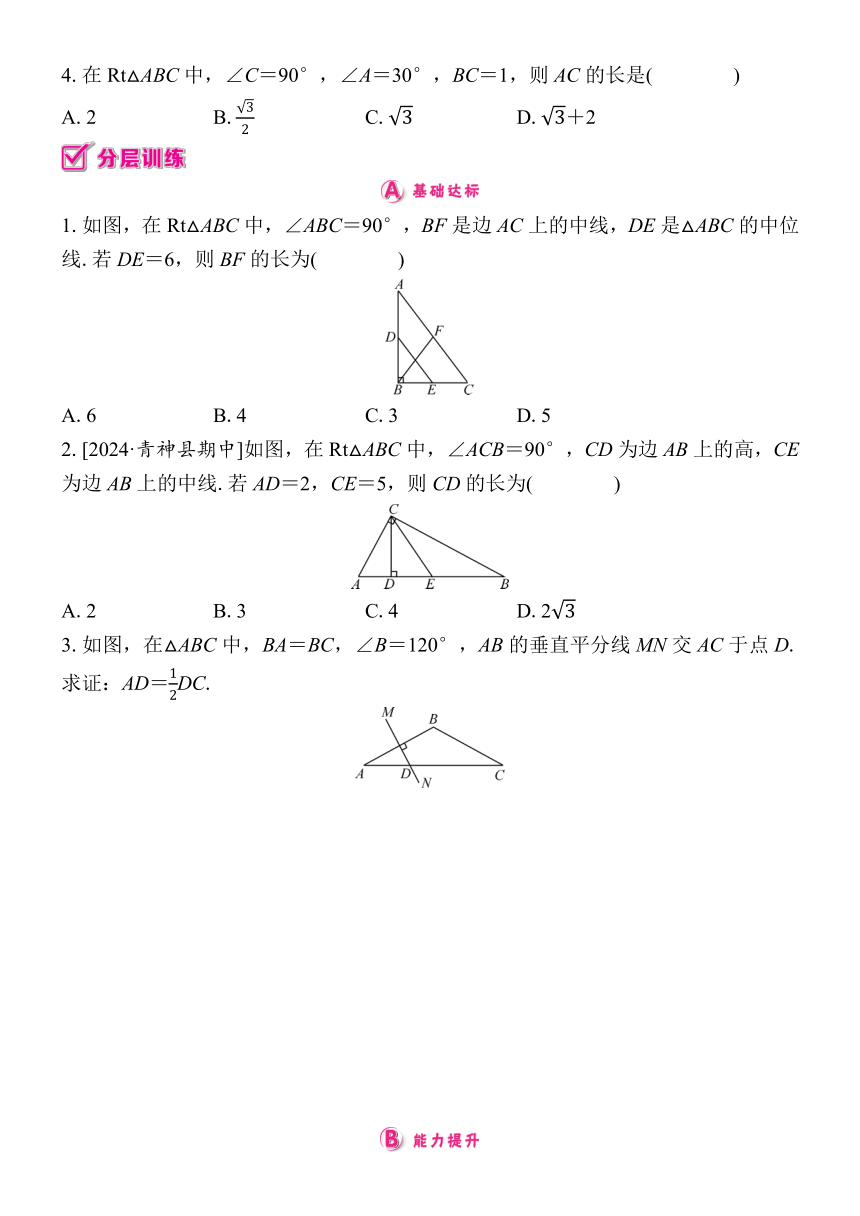
4.在Rt△ABC中,∠C=90°,∠A=30°,BC=1,则AC的长是( )
A.2 B. C. D.+2
1.如图,在Rt△ABC中,∠ABC=90°,BF是边AC上的中线,DE是△ABC的中位线.若DE=6,则BF的长为( )
A.6 B.4 C.3 D.5
2.[2024·青神县期中]如图,在Rt△ABC中,∠ACB=90°,CD为边AB上的高,CE为边AB上的中线.若AD=2,CE=5,则CD的长为( )
A.2 B.3 C.4 D.2
3.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于点D.求证:AD=DC.
4.[2023·赤峰]如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点F是AB的中点,连结CF,把线段CF沿射线BC的方向平移到DE,点D在AC上,则线段CF在平移过程中扫过的区域是四边形CFDE,则四边形CFDE的周长和面积分别是( )
A.16、6 B.18、18
C.16、12 D.12、16
5.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于点D.若PC=5,则PD= .
6.如图,在四边形ABCD中,∠ABC=90°,AC=AD,点M、N分别为AC、CD的中点,连结BM、MN、BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
7.如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.求证:
(1)四边形ADEF是平行四边形;
(2)∠DHF=∠DEF.
8.(推理能力)如图,在Rt△ABC中,∠C=90°,∠ABD=2∠EBC,AD∥BC.求证:DE=2AB.
参考答案
【预习导航】
互余 斜边的平方 斜边的一半
【归类探究】
【例1】(1)略
(2)∠DNE=180°-2∠A,理由略.
【例2】略
【例3】略
【当堂测评】
1.D 2.B 3.D 4.C
【分层训练】
1.A 2.C 3.略 4.C 5.
6.(1)略 (2)BN=
7.略 8.略
。
24.2 直角三角形的性质
1.直角三角形的性质
锐角关系:直角三角形的两个锐角 .
勾股定理:直角三角形两直角边的平方和等于 .
2.直角三角形斜边上的中线
性 质:直角三角形斜边上的中线等于 .
3.含30°角的直角三角形的性质
性 质:在直角三角形中,30°角所对的直角边等于斜边的一半.
类型之一 直角三角形斜边上的中线的性质
[2024·江都区期末]如图,在锐角三角形ABC中,CD、BE分别是边AB、AC上的高,点M、N分别是线段DE、BC的中点.
(1)求证:MN⊥DE;
(2)连结DN、EN,猜想∠A与∠DNE之间的关系,并说明理由.
类型之二 含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.试作出图形,写出已知、求证,并给出证明.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠A=30°.求证:BD=AB.
1.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M、C两点间的距离为( )
A.0.5km B.0.6km
C.0.9km D.1.2km
2.[2023·株洲]一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB=90°,点D为边AB的中点,点A、B对应的刻度分别为1、7,则CD的长为( )
A.3.5cm B.3cm C.4.5cm D.6cm
3.如图,在Rt△ABC中,∠C=90°,AC=3,∠B=30°,点P是边BC上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
4.在Rt△ABC中,∠C=90°,∠A=30°,BC=1,则AC的长是( )
A.2 B. C. D.+2
1.如图,在Rt△ABC中,∠ABC=90°,BF是边AC上的中线,DE是△ABC的中位线.若DE=6,则BF的长为( )
A.6 B.4 C.3 D.5
2.[2024·青神县期中]如图,在Rt△ABC中,∠ACB=90°,CD为边AB上的高,CE为边AB上的中线.若AD=2,CE=5,则CD的长为( )
A.2 B.3 C.4 D.2
3.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于点D.求证:AD=DC.
4.[2023·赤峰]如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点F是AB的中点,连结CF,把线段CF沿射线BC的方向平移到DE,点D在AC上,则线段CF在平移过程中扫过的区域是四边形CFDE,则四边形CFDE的周长和面积分别是( )
A.16、6 B.18、18
C.16、12 D.12、16
5.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于点D.若PC=5,则PD= .
6.如图,在四边形ABCD中,∠ABC=90°,AC=AD,点M、N分别为AC、CD的中点,连结BM、MN、BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
7.如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.求证:
(1)四边形ADEF是平行四边形;
(2)∠DHF=∠DEF.
8.(推理能力)如图,在Rt△ABC中,∠C=90°,∠ABD=2∠EBC,AD∥BC.求证:DE=2AB.
参考答案
【预习导航】
互余 斜边的平方 斜边的一半
【归类探究】
【例1】(1)略
(2)∠DNE=180°-2∠A,理由略.
【例2】略
【例3】略
【当堂测评】
1.D 2.B 3.D 4.C
【分层训练】
1.A 2.C 3.略 4.C 5.
6.(1)略 (2)BN=
7.略 8.略
。
