数学:2.4.3《等比数列复习课》课件(新人教a版必修5)
文档属性
| 名称 | 数学:2.4.3《等比数列复习课》课件(新人教a版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-11 00:00:00 | ||
图片预览







文档简介
课件21张PPT。新课标人教版课件系列《高中数学》
必修52.4.3《等比数列复习课》审校:王伟1.定义:an/an-1=q (q为常数)(n≥2)3.等比数列的通项变形公式:
an=amqn-m 2.等比数列的通项公式:an=a1qn-18.等比数列的前 项和公式:
或a1、q、n、an、Sn中
知三求二9.性质: 在等比数列{an}中,Sn是它的前n项和,
那么有:
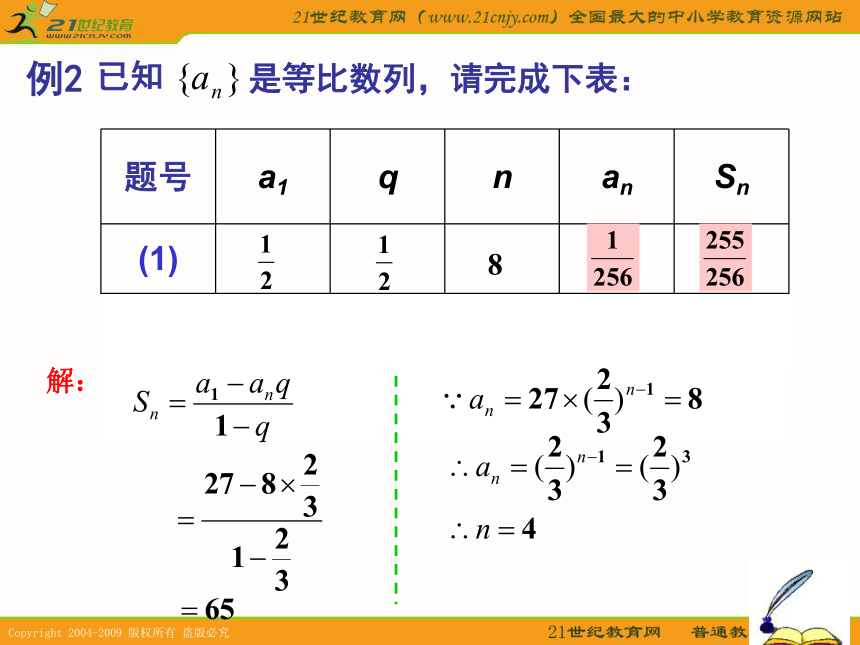
Sm, S2m-Sm, S3m-S2m, 也成等比数列. n+1判断是非②n点 击③若 且 ,则c2≠1①2n新课讲授:已知是等比数列,请完成下表:例1解:?已知是等比数列,请完成下表:例2解:已知是等比数列,请完成下表:a1、q、n、an、Sn中
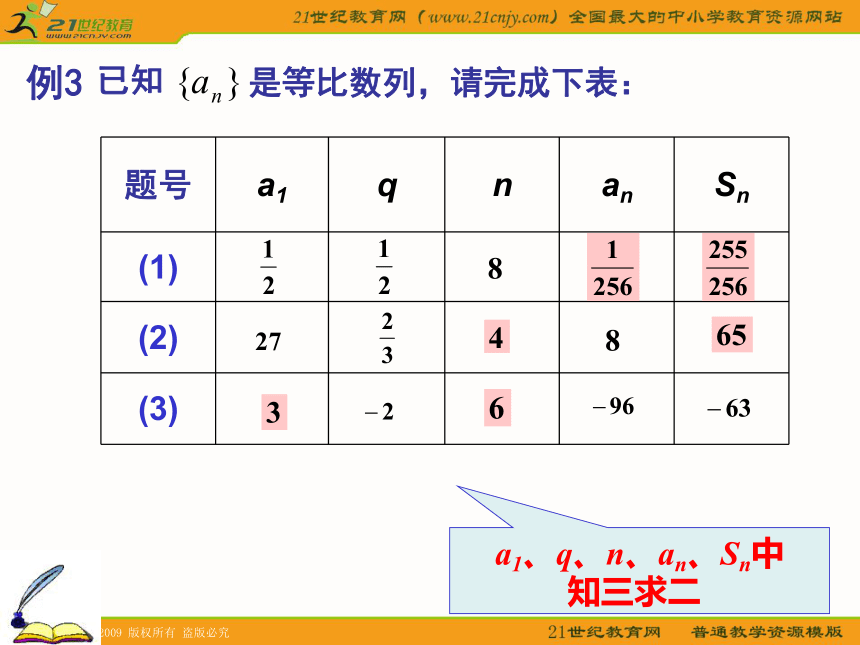
例3知三求二例4 求等比数列 的第5项到第10项的和.【解法1】例5. 已知等比数列{an}的前 m项和为10,
前 2m项和为50,求它的前 3m项的和。
解: 在等比数列{an}中,有:Sm, S2m-Sm, S3m-S2m, 也成等比数列.
所以,由 (S2m-Sm)2=Sm× (S3m-S2m)得:
S3m=210 求数列 的前n项的和.拓展1分组求和反思解:求和:拓展2(2)当 ,即 时原式= 例6.从盛满 升( )纯酒精的容器里倒出1 升,然后填满水,再倒出1升混合溶液后又用水填满,如此继续下去.问第 次操作后溶液的浓度是多少?若 ,至少应倒几次后才能使酒精浓度低于 ? 分析:这是一道数学应用题.解决应用问题的关键是建立数学模型,使实际问题数学化.注意到开始浓度为1,操作一次后溶液浓度是 .操作二次后溶液浓度是 ,…,操作n次后溶液浓度是 .则不难发现,每次操作后溶液浓度构成等比数列,由此便建立了数列模型.解决数列问题,便可能达到解决实际问题之目的. 有关等比数列的应用题解:设每次操作后溶液浓度为数列 ,则问题即为求数列的通项 .
依题意,知原浓度为1, , ,…, .
构成以首项 ,公比 的等比数列,
所以 ,
故第n次操作后酒精浓度是 当 时,
由 ,得 .
因此,至少应操作4次后,才能使酒精浓度低于 .注:数学应用问题的解答步骤:
一、通过阅读,理解题意,建立数学模型;
二、通过解决数学问题,解决实际问题;
三、回答实际问题. 例7.某人年初欲向银行贷款10万元用于买房。已知有以下两种还款方式:
(Ⅰ)等额本息还款法:分10次等额归还,年利 率为4%,按复利计算,每年年初还款一次;
(Ⅱ)等额本金还款法:每年年初还本金1万元,并加付欠款的利息,年利率为5%;
请问:他用哪一种还款方式比较合算?(1) 解法1: 设每年还款m元 .
105×1.0410 = m (1+4%)9 + m (1+4%)8 + m (1+4%)7 +…… + m
= m (1.049 + 1.048 + 1.047 + … + 1.04 +1)
= 解得 m = ≈12330 (元)
即每年需还款12330元.实际房款为1233010=123300元解法2:设每年还款m元 , n年后欠款余额为an元 . 则
a1=105× (1+4%)–m
a2=[105× (1+4%)–m] (1+4%)–m=105×1.042–1.04m–m
a3=(105×1.042–1.04m–m) (1+4%)–m =105 ×1.043–1.042m–1.04m–m
……
a10=105-1.049 m -1.048 m -1.047-……-1.04 m - m
=105×1.0410- m (1.049 + 1.048 + 1.047 + … + 1.04 +1)
=105×1.0410- =105 ×1.4802 -
根据题意a10=0 解得 m = ≈12330 (元)所以,每年需还款12330元. (2)设每年交付欠款的数额顺次构成数列{an},故
a1=104+105×0.05=15000(元)
a2=104+(105-104) ×0.05=14500(元)
a3=104+(105-104×2) ×0.05=14000(元)
a4 =104+(105-104×3) ×0.05=13500(元)
……
an =104+[105-104× (n-1)] ×0.05=15500-500n (1≤n≤10,n∈N)
∴{ an }是以15000为首项,-500为公差的等差数列.
∴10次分期付款总和为
(元)(比较两种还款法的具体情况):应选择(Ⅱ) 新人教版必修5
练习: 课本76~77. A组6~10
B组3, 7
作业: 课本P77. B组 4~6再见
必修52.4.3《等比数列复习课》审校:王伟1.定义:an/an-1=q (q为常数)(n≥2)3.等比数列的通项变形公式:
an=amqn-m 2.等比数列的通项公式:an=a1qn-18.等比数列的前 项和公式:
或a1、q、n、an、Sn中
知三求二9.性质: 在等比数列{an}中,Sn是它的前n项和,
那么有:
Sm, S2m-Sm, S3m-S2m, 也成等比数列. n+1判断是非②n点 击③若 且 ,则c2≠1①2n新课讲授:已知是等比数列,请完成下表:例1解:?已知是等比数列,请完成下表:例2解:已知是等比数列,请完成下表:a1、q、n、an、Sn中
例3知三求二例4 求等比数列 的第5项到第10项的和.【解法1】例5. 已知等比数列{an}的前 m项和为10,
前 2m项和为50,求它的前 3m项的和。
解: 在等比数列{an}中,有:Sm, S2m-Sm, S3m-S2m, 也成等比数列.
所以,由 (S2m-Sm)2=Sm× (S3m-S2m)得:
S3m=210 求数列 的前n项的和.拓展1分组求和反思解:求和:拓展2(2)当 ,即 时原式= 例6.从盛满 升( )纯酒精的容器里倒出1 升,然后填满水,再倒出1升混合溶液后又用水填满,如此继续下去.问第 次操作后溶液的浓度是多少?若 ,至少应倒几次后才能使酒精浓度低于 ? 分析:这是一道数学应用题.解决应用问题的关键是建立数学模型,使实际问题数学化.注意到开始浓度为1,操作一次后溶液浓度是 .操作二次后溶液浓度是 ,…,操作n次后溶液浓度是 .则不难发现,每次操作后溶液浓度构成等比数列,由此便建立了数列模型.解决数列问题,便可能达到解决实际问题之目的. 有关等比数列的应用题解:设每次操作后溶液浓度为数列 ,则问题即为求数列的通项 .
依题意,知原浓度为1, , ,…, .
构成以首项 ,公比 的等比数列,
所以 ,
故第n次操作后酒精浓度是 当 时,
由 ,得 .
因此,至少应操作4次后,才能使酒精浓度低于 .注:数学应用问题的解答步骤:
一、通过阅读,理解题意,建立数学模型;
二、通过解决数学问题,解决实际问题;
三、回答实际问题. 例7.某人年初欲向银行贷款10万元用于买房。已知有以下两种还款方式:
(Ⅰ)等额本息还款法:分10次等额归还,年利 率为4%,按复利计算,每年年初还款一次;
(Ⅱ)等额本金还款法:每年年初还本金1万元,并加付欠款的利息,年利率为5%;
请问:他用哪一种还款方式比较合算?(1) 解法1: 设每年还款m元 .
105×1.0410 = m (1+4%)9 + m (1+4%)8 + m (1+4%)7 +…… + m
= m (1.049 + 1.048 + 1.047 + … + 1.04 +1)
= 解得 m = ≈12330 (元)
即每年需还款12330元.实际房款为1233010=123300元解法2:设每年还款m元 , n年后欠款余额为an元 . 则
a1=105× (1+4%)–m
a2=[105× (1+4%)–m] (1+4%)–m=105×1.042–1.04m–m
a3=(105×1.042–1.04m–m) (1+4%)–m =105 ×1.043–1.042m–1.04m–m
……
a10=105-1.049 m -1.048 m -1.047-……-1.04 m - m
=105×1.0410- m (1.049 + 1.048 + 1.047 + … + 1.04 +1)
=105×1.0410- =105 ×1.4802 -
根据题意a10=0 解得 m = ≈12330 (元)所以,每年需还款12330元. (2)设每年交付欠款的数额顺次构成数列{an},故
a1=104+105×0.05=15000(元)
a2=104+(105-104) ×0.05=14500(元)
a3=104+(105-104×2) ×0.05=14000(元)
a4 =104+(105-104×3) ×0.05=13500(元)
……
an =104+[105-104× (n-1)] ×0.05=15500-500n (1≤n≤10,n∈N)
∴{ an }是以15000为首项,-500为公差的等差数列.
∴10次分期付款总和为
(元)(比较两种还款法的具体情况):应选择(Ⅱ) 新人教版必修5
练习: 课本76~77. A组6~10
B组3, 7
作业: 课本P77. B组 4~6再见
