4.2概率及其计算 课件 (2)(17PPT)
文档属性
| 名称 | 4.2概率及其计算 课件 (2)(17PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 580.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览





文档简介
课件17张PPT。4.2.1 概率的概念湘教版 九年级下册4.2 概率及其计算 在随机现象中,出现的各种可能的结果共有n种,如果出现其中每一种结果的可能性大小是一样的,那么出现每一种结果的概率都是 .在随机现象中,如果事件A包含m种可能的结果,那么出现这个事件的概率记作P(A).
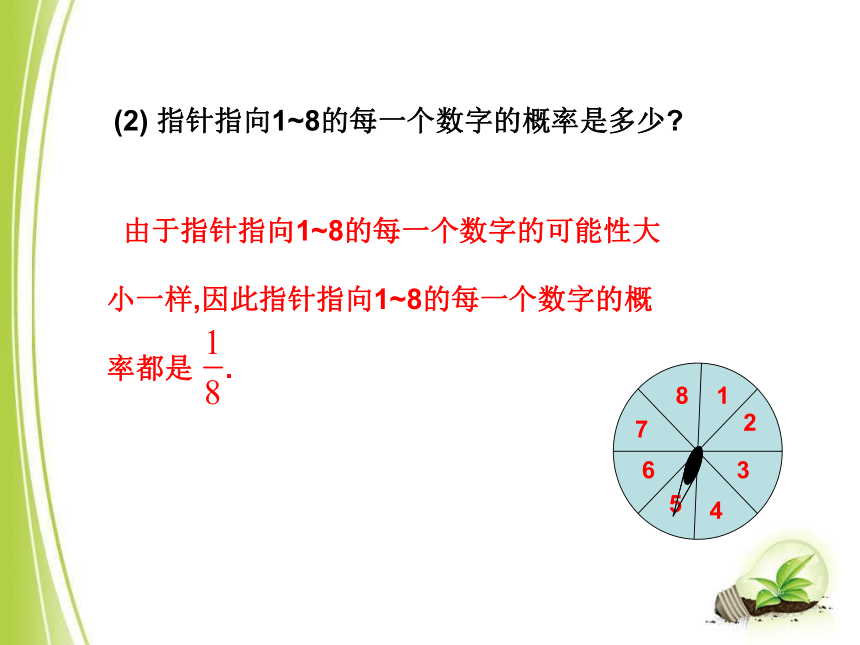
圆盘被分成8个全等的小扇形,分别写上数字1,2,3,4,5,6,7,8.自由转动圆盘,试问:
(1)可能出现的结果有几种?
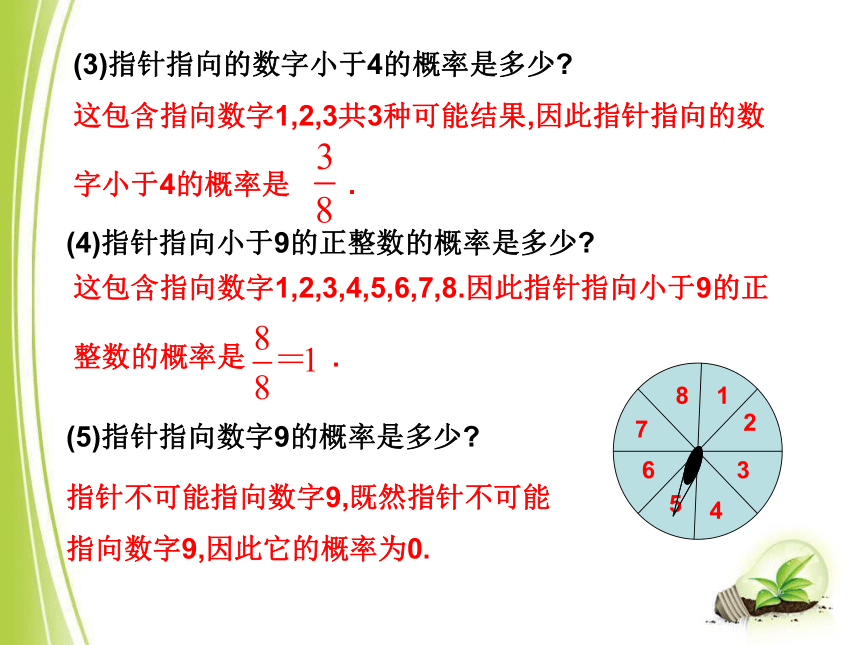
有8种:指针指向数字1,指向数字2,…,指向数字8.1234567812345678(2) 指针指向1~8的每一个数字的概率是多少? 由于指针指向1~8的每一个数字的可能性大小一样,因此指针指向1~8的每一个数字的概率都是 .这包含指向数字1,2,3共3种可能结果,因此指针指向的数字小于4的概率是 . 这包含指向数字1,2,3,4,5,6,7,8.因此指针指向小于9的正整数的概率是 .指针不可能指向数字9,既然指针不可能
指向数字9,因此它的概率为0.(3)指针指向的数字小于4的概率是多少? (4)指针指向小于9的正整数的概率是多少?(5)指针指向数字9的概率是多少? 在一定条件下,必然会发生的事情称为必然事件;一定不会发生的事情称为不可能事件.它们可看成是随机事件的两个极端情形.
1.必然事件的概率为P(A)=1;
2.不可能事件的概率为P(A)= 0.事件发生的可能性越来越大事件发生的可能性越来越小不可能事件必然事件概率的值3.不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为(正,正), (正,反), (反,正), (反,反). 1.掷一枚硬币两次,可能出现的结果有几种?答: 至少有一次出现正面包含(正,正),(正,反),(反,正)3种可能结果,因此至少有一次出现正面的概率是 .答;可能性大小相等,概率都是 .掷一枚硬币两次,出现上述每一种结果的概率是多少?(2) 掷一枚硬币两次,至少有一次出现正面的概率是多少?2.某班在新年晚会上做了一个游戏:袋中装有1个红球,3各黑球,11个白球,它们除颜色外,其他地方没有差别.从袋中随意取出一个球,如果取出的是红球,那么获一等奖;如果取出的是黑球那么获二等奖;如果取出的是白球,那么没有中奖.试问:获一等奖、二等奖的概率各是多少?解:袋中一共有1+3+11=15个球.从袋中随意取出一个球,每一个球被取出的概率都是 .由于袋中有1个红球,3个黑球,
因此
即,获一等奖、二等奖的概率分别是1.从标有1,2,3…,20的20张卡片中任意抽取一张,以下事件可能性最大的是( )
A.卡片上的数字是2 的倍数.
B.卡片上的数字是3的倍数.
C.卡片上的数字是4 的倍数.
D.卡片上的数字是5的倍数.2.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=3.(2变式 ) 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。 解:掷1个质地均匀的正方体骰子,向上一面的点数可能为1,2,3,4,5,6,共6种。这些点数出现的可能性相等。.(1)掷得点数为2或4或6(记为事件A)有3种结果,因此P(A) ;(2)小明前五次都没掷得点数2,可他第六次掷得点数仍然可能为1,2,3,4,5,6,共6种。他第六次掷得点数2(记为事件B)有1种结果,因此P(B) .1.在随机现象中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 2 .必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0<P(C)<1。从教材习题中选取。
课后作业
圆盘被分成8个全等的小扇形,分别写上数字1,2,3,4,5,6,7,8.自由转动圆盘,试问:
(1)可能出现的结果有几种?
有8种:指针指向数字1,指向数字2,…,指向数字8.1234567812345678(2) 指针指向1~8的每一个数字的概率是多少? 由于指针指向1~8的每一个数字的可能性大小一样,因此指针指向1~8的每一个数字的概率都是 .这包含指向数字1,2,3共3种可能结果,因此指针指向的数字小于4的概率是 . 这包含指向数字1,2,3,4,5,6,7,8.因此指针指向小于9的正整数的概率是 .指针不可能指向数字9,既然指针不可能
指向数字9,因此它的概率为0.(3)指针指向的数字小于4的概率是多少? (4)指针指向小于9的正整数的概率是多少?(5)指针指向数字9的概率是多少? 在一定条件下,必然会发生的事情称为必然事件;一定不会发生的事情称为不可能事件.它们可看成是随机事件的两个极端情形.
1.必然事件的概率为P(A)=1;
2.不可能事件的概率为P(A)= 0.事件发生的可能性越来越大事件发生的可能性越来越小不可能事件必然事件概率的值3.不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为(正,正), (正,反), (反,正), (反,反). 1.掷一枚硬币两次,可能出现的结果有几种?答: 至少有一次出现正面包含(正,正),(正,反),(反,正)3种可能结果,因此至少有一次出现正面的概率是 .答;可能性大小相等,概率都是 .掷一枚硬币两次,出现上述每一种结果的概率是多少?(2) 掷一枚硬币两次,至少有一次出现正面的概率是多少?2.某班在新年晚会上做了一个游戏:袋中装有1个红球,3各黑球,11个白球,它们除颜色外,其他地方没有差别.从袋中随意取出一个球,如果取出的是红球,那么获一等奖;如果取出的是黑球那么获二等奖;如果取出的是白球,那么没有中奖.试问:获一等奖、二等奖的概率各是多少?解:袋中一共有1+3+11=15个球.从袋中随意取出一个球,每一个球被取出的概率都是 .由于袋中有1个红球,3个黑球,
因此
即,获一等奖、二等奖的概率分别是1.从标有1,2,3…,20的20张卡片中任意抽取一张,以下事件可能性最大的是( )
A.卡片上的数字是2 的倍数.
B.卡片上的数字是3的倍数.
C.卡片上的数字是4 的倍数.
D.卡片上的数字是5的倍数.2.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=3.(2变式 ) 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。 解:掷1个质地均匀的正方体骰子,向上一面的点数可能为1,2,3,4,5,6,共6种。这些点数出现的可能性相等。.(1)掷得点数为2或4或6(记为事件A)有3种结果,因此P(A) ;(2)小明前五次都没掷得点数2,可他第六次掷得点数仍然可能为1,2,3,4,5,6,共6种。他第六次掷得点数2(记为事件B)有1种结果,因此P(B) .1.在随机现象中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 2 .必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0<P(C)<1。从教材习题中选取。
课后作业
