4.3用频率估计概率 课件 (3)(25PPT)
文档属性
| 名称 | 4.3用频率估计概率 课件 (3)(25PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 646.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 19:08:07 | ||
图片预览








文档简介
课件25张PPT。用频率来估计概率4.3抛掷一枚质地均匀的硬币时,“正面向上”和“反面向上”发生的可能性相等,这两个随机事件发生的概率分别是 .
这是否意味着抛掷一枚硬币100次时,就会有50次“正面向上”和50次“反面向上”呢?知识回顾 我们知道,抛掷一枚均匀硬币,硬币落地后,
出现“正面朝上” 的可能性和“反面朝上” 的
可能性是一样的, 即“正面朝上” 的概率和
“反面朝上” 的概率都是 . 在实际掷硬币时,会出现什么情况? 若只抛
一次说明不了什么问题,我们不妨多抛掷几次试试.
把全班同学分成10组,每组同学掷一枚硬币50次,把本组的试验数据进行统计,“正面向上”和“反面
向上”的频数和频率分别是多少?
请同学们以小组形式来展示本组的研究结果. 在多次试验中,某个事件出现的次数叫 ,
某个事件出现的次数与试验总次数的比,叫做这个事件
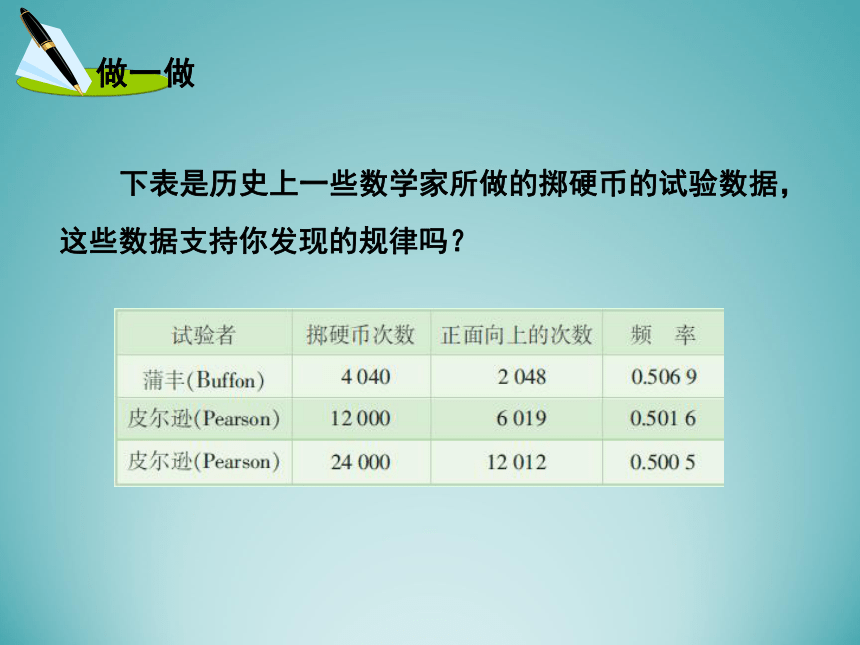
出现的 .频数频率 下表是历史上一些数学家所做的掷硬币的试验数据,
这些数据支持你发现的规律吗?材料: 在重复抛掷一枚硬币时,“正面向上”的频率在0.5左右摆动.随着抛掷
次数的增加,一般的,频率呈现一定的稳定性:在0.5左右摆动的幅度会
越来越小.这时,我们称“正面向上”的频率稳定于0.5.思考:随着抛掷次数的增加,“正面向上”的频率的变化
趋势有何变化?可以看出,随着掷硬币次数的增加, “正面朝上” 的频率稳定在 左右. 从长期的实践中,人们观察到,对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数值的附近摆动,显示出一定的稳定性. 上面的例子说明,通过大量重复试验,可以用随机事件发生的频率来估计该事件发生的概率. 对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用4.2节的方法来求概率. 频率是否可以估计该随机事件的概率呢? 一般地,在大量重复试验中,如果事件 A发生的频率 稳定于某个常数 p ,那么事件A 发生的概率 P(A)= p. 用频率估计的概率可能小于0吗?可能大于1吗?数学史实 瑞士数学家雅各布·伯努利(1654-1705)被公认为是概率论
的先驱之一,他最早阐明了随着
试验次数的增加,频率稳定在概
率附近. 因此,掷100次硬币并不一定能得到“正面朝上” 的频率是 ,“反面朝上”的频率是 . 而概率是刻画随机事件发生可能性大小的数值,是
一个固定的量,不具有随机性. 需要指出的是,频率和概率都是随机事件可能性大
小的定量的刻画,但频率与试验次数及具体的试验有关,因此,频率具有随机性;举
例例 瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生哪种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.举
例 某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,
结果如下:(1) 计算上表中合格品的各频率(精确到0.001);(2) 估计这种瓷砖的合格品率(精确到0.01);(3) 若该工厂本月生产该型号瓷砖500000 块,试估计合格品数.举
例解(1) 逐项计算, 填表如下:举
例(2) 观察上表,可以发现,当抽取的瓷砖数n≥400 时,合格品频率 稳定在0.962 的附近,所以我们可取p = 0.96 作为该型号瓷砖的合格品率的估计.(3) 500000 × 96%= 480000(块),可以估计该型号合格品数为480000 块.了解了一种方法--用多次试验所得的频率去估计概率体会了一种思想:用样本去估计总体
用频率去估计概率弄清了一种关系--频率与概率的关系 当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.1、某校进行篮球“3分球” 比赛,下表是对某篮球队员进行测试的结果:(1)根据上表,估计该运动员投3分球命中的概率是多少;(2)根据上表,假设该运动员在一场比赛中有20次投3分球的机会,估计他能得多少分.习题解答:
(1)P(该运动员投3分球命中)=0.72
(2) 0.72×20×3≈43(分)习题2、某射手在同一条件下进行射击,结果如下:(1) 计算上表中击中靶心的各个频率,并填入表格中;
(2) 这个射手射击一次,击中靶心的概率约为多少?解:
(1)习题0.90.950.880.910.890.902复习题二某科技小组做黄豆在相同条件下的发芽试验,结果如下表所示:则黄豆发芽的概率估计值是多少?解答:P(黄豆发芽)=0.95.例 在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是多少?(2013年湖南中考)考点: 利用频率估计概率.
分析: 在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.
解答:由题意可得, =0.2,解得,n=10.故估计盒子中 共装有大约有10个小球.故答案为10.结 束
这是否意味着抛掷一枚硬币100次时,就会有50次“正面向上”和50次“反面向上”呢?知识回顾 我们知道,抛掷一枚均匀硬币,硬币落地后,
出现“正面朝上” 的可能性和“反面朝上” 的
可能性是一样的, 即“正面朝上” 的概率和
“反面朝上” 的概率都是 . 在实际掷硬币时,会出现什么情况? 若只抛
一次说明不了什么问题,我们不妨多抛掷几次试试.
把全班同学分成10组,每组同学掷一枚硬币50次,把本组的试验数据进行统计,“正面向上”和“反面
向上”的频数和频率分别是多少?
请同学们以小组形式来展示本组的研究结果. 在多次试验中,某个事件出现的次数叫 ,
某个事件出现的次数与试验总次数的比,叫做这个事件
出现的 .频数频率 下表是历史上一些数学家所做的掷硬币的试验数据,
这些数据支持你发现的规律吗?材料: 在重复抛掷一枚硬币时,“正面向上”的频率在0.5左右摆动.随着抛掷
次数的增加,一般的,频率呈现一定的稳定性:在0.5左右摆动的幅度会
越来越小.这时,我们称“正面向上”的频率稳定于0.5.思考:随着抛掷次数的增加,“正面向上”的频率的变化
趋势有何变化?可以看出,随着掷硬币次数的增加, “正面朝上” 的频率稳定在 左右. 从长期的实践中,人们观察到,对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数值的附近摆动,显示出一定的稳定性. 上面的例子说明,通过大量重复试验,可以用随机事件发生的频率来估计该事件发生的概率. 对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用4.2节的方法来求概率. 频率是否可以估计该随机事件的概率呢? 一般地,在大量重复试验中,如果事件 A发生的频率 稳定于某个常数 p ,那么事件A 发生的概率 P(A)= p. 用频率估计的概率可能小于0吗?可能大于1吗?数学史实 瑞士数学家雅各布·伯努利(1654-1705)被公认为是概率论
的先驱之一,他最早阐明了随着
试验次数的增加,频率稳定在概
率附近. 因此,掷100次硬币并不一定能得到“正面朝上” 的频率是 ,“反面朝上”的频率是 . 而概率是刻画随机事件发生可能性大小的数值,是
一个固定的量,不具有随机性. 需要指出的是,频率和概率都是随机事件可能性大
小的定量的刻画,但频率与试验次数及具体的试验有关,因此,频率具有随机性;举
例例 瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生哪种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.举
例 某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,
结果如下:(1) 计算上表中合格品的各频率(精确到0.001);(2) 估计这种瓷砖的合格品率(精确到0.01);(3) 若该工厂本月生产该型号瓷砖500000 块,试估计合格品数.举
例解(1) 逐项计算, 填表如下:举
例(2) 观察上表,可以发现,当抽取的瓷砖数n≥400 时,合格品频率 稳定在0.962 的附近,所以我们可取p = 0.96 作为该型号瓷砖的合格品率的估计.(3) 500000 × 96%= 480000(块),可以估计该型号合格品数为480000 块.了解了一种方法--用多次试验所得的频率去估计概率体会了一种思想:用样本去估计总体
用频率去估计概率弄清了一种关系--频率与概率的关系 当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.1、某校进行篮球“3分球” 比赛,下表是对某篮球队员进行测试的结果:(1)根据上表,估计该运动员投3分球命中的概率是多少;(2)根据上表,假设该运动员在一场比赛中有20次投3分球的机会,估计他能得多少分.习题解答:
(1)P(该运动员投3分球命中)=0.72
(2) 0.72×20×3≈43(分)习题2、某射手在同一条件下进行射击,结果如下:(1) 计算上表中击中靶心的各个频率,并填入表格中;
(2) 这个射手射击一次,击中靶心的概率约为多少?解:
(1)习题0.90.950.880.910.890.902复习题二某科技小组做黄豆在相同条件下的发芽试验,结果如下表所示:则黄豆发芽的概率估计值是多少?解答:P(黄豆发芽)=0.95.例 在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是多少?(2013年湖南中考)考点: 利用频率估计概率.
分析: 在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.
解答:由题意可得, =0.2,解得,n=10.故估计盒子中 共装有大约有10个小球.故答案为10.结 束
