5.4二次函数与一元二次方程(含解析)苏科版九年级数学下册
文档属性
| 名称 | 5.4二次函数与一元二次方程(含解析)苏科版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 808.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览


文档简介
5.4二次函数与一元二次方程
一、单选题
1.如图,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是﹣3,顶点坐标为(﹣1,4),则下列说法正确的是( )
A.二次函数图象的对称轴是直线x=1
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当x<﹣1时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0; ②b2<4ac; ③2c<3b; ④a+2b>m(am+b)(m≠1);
⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为2,
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
3.表中列出的是一个二次函数的自变量x与函数y的几组对应值:
x … ﹣2 0 1 3 …
y … 6 ﹣4 ﹣6 ﹣4 …
下列各选项中,正确的是( )
A.这个函数的最小值为﹣6
B.这个函数的图象开口向下
C.这个函数的图象与x轴无交点
D.当x>2时,y的值随x值的增大而增大
4.二次函数y=ax2+bx+c的图象如图所示.下列结论:
①2a+b=0;
②a+b+c>0;
③方程ax2+bx+c=a有两个不相等的实数根;
④不等式a(x+1)2+b(x+1)+c<0的解集是﹣2<x<2.
其中所有正确结论的序号是( )
A.①③ B.②④ C.①③④ D.①②③④
5.如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点A的横坐标的最大值为2,则点B的横坐标的最小值为( )
A.1 B.2 C.3 D.4
二、填空题
6.已知二次函数y=﹣x2+2x+m的图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的根为 ;不等式﹣x2+2x+m>0的解集是 ;当x 时,y随x的增大而减小.
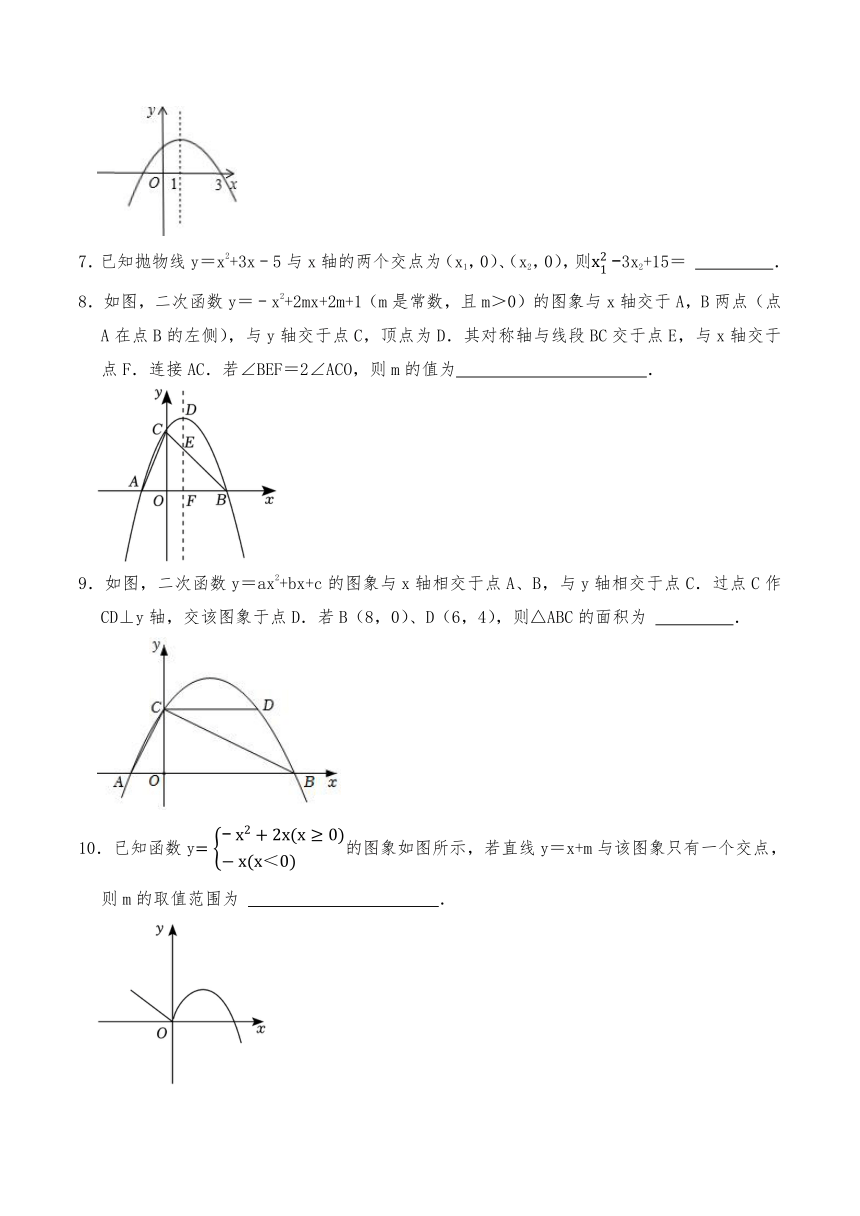
7.已知抛物线y=x2+3x﹣5与x轴的两个交点为(x1,0)、(x2,0),则3x2+15= .
8.如图,二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC.若∠BEF=2∠ACO,则m的值为 .
9.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C.过点C作CD⊥y轴,交该图象于点D.若B(8,0)、D(6,4),则△ABC的面积为 .
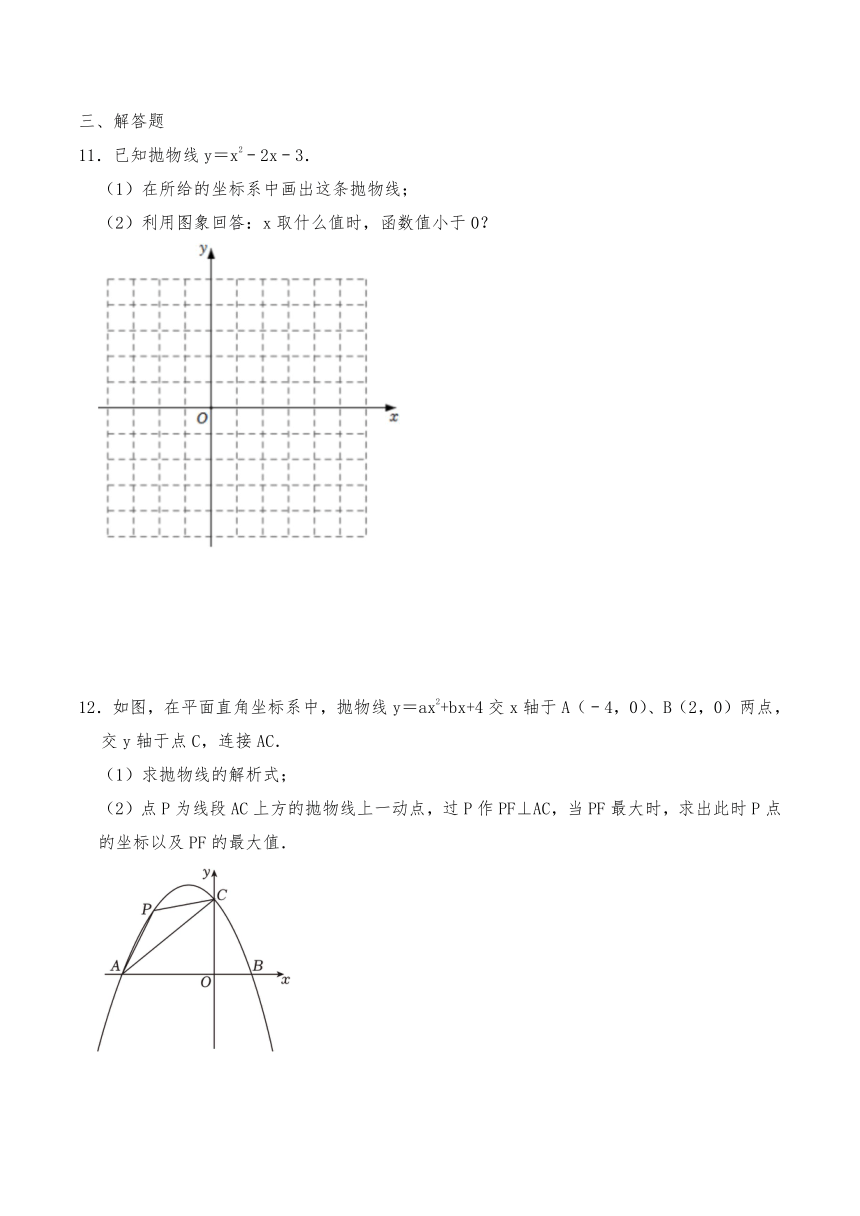
10.已知函数y的图象如图所示,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .
三、解答题
11.已知抛物线y=x2﹣2x﹣3.
(1)在所给的坐标系中画出这条抛物线;
(2)利用图象回答:x取什么值时,函数值小于0?
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于A(﹣4,0)、B(2,0)两点,交y轴于点C,连接AC.
(1)求抛物线的解析式;
(2)点P为线段AC上方的抛物线上一动点,过P作PF⊥AC,当PF最大时,求出此时P点的坐标以及PF的最大值.
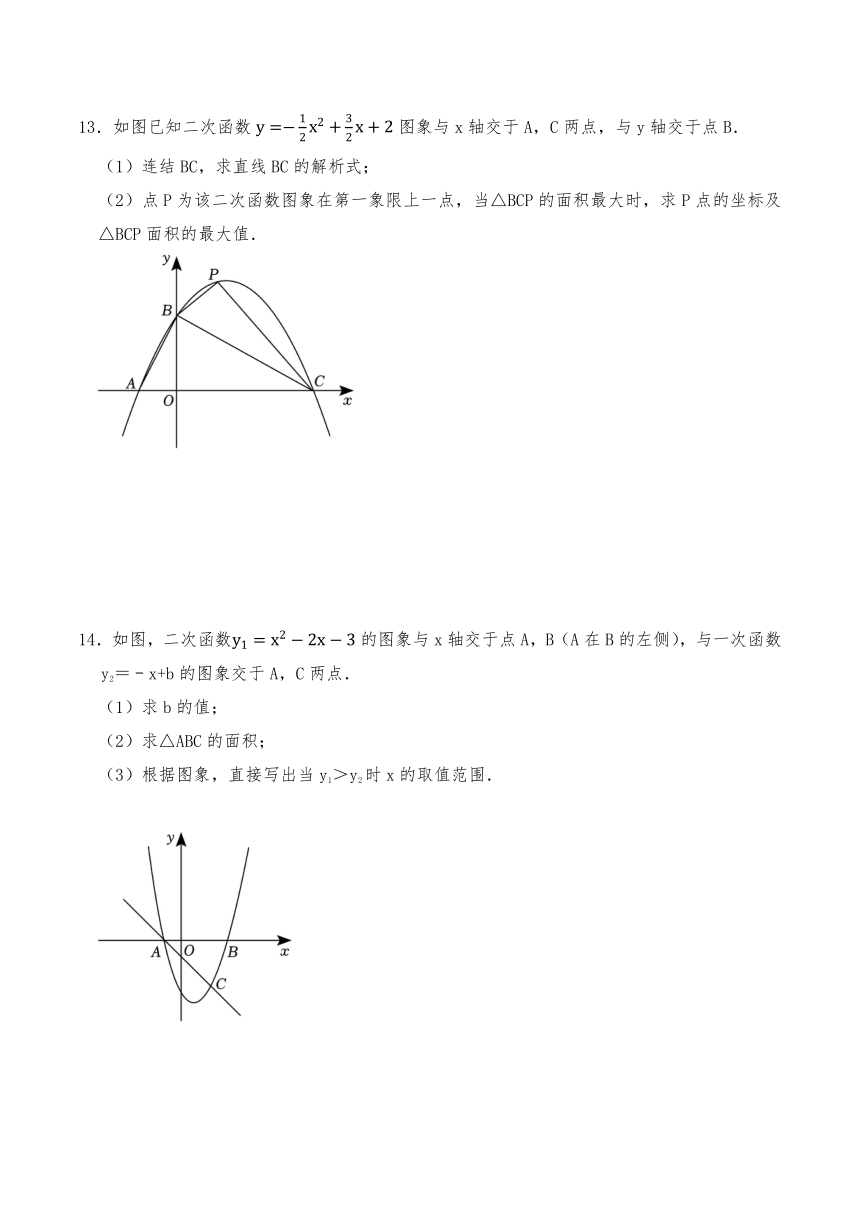
13.如图已知二次函数图象与x轴交于A,C两点,与y轴交于点B.
(1)连结BC,求直线BC的解析式;
(2)点P为该二次函数图象在第一象限上一点,当△BCP的面积最大时,求P点的坐标及△BCP面积的最大值.
14.如图,二次函数的图象与x轴交于点A,B(A在B的左侧),与一次函数y2=﹣x+b的图象交于A,C两点.
(1)求b的值;
(2)求△ABC的面积;
(3)根据图象,直接写出当y1>y2时x的取值范围.
15.二次函数y=x2+bx+c的图象经过点A(1,0),B(0,3),点C与点B关于该二次函数图象的对称轴对称,已知一次函数y=mx+n的图象经过A,C两点.
(1)求二次函数解析式;
(2)根据图象,写出满足不等式x2+bx+c<mx+n的解集 ;
(3)二次函数y=x2+bx+c,当1≤x≤3时,对应的函数值y的取值范围为 .
16.如图,二次函数图象顶点坐标为(﹣1,﹣4),与x轴一个交点坐标为(1,0).
(1)该函数图象与x轴的另一个交点坐标为 ;
(2)求这个二次函数的表达式;
(3)当﹣4<x<0时,y的取值范围为 .
17.如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C.
(1)求抛物线对应的函数解析式,并直接写出顶点P的坐标;
(2)求△BCP的面积.
注:注抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣,顶点坐标是(,).
18.如图,在平面直角坐标系中,抛物线L1交x轴于点A(1,0),C(5,0),顶点坐标为E(m1,k).抛物线L2交x轴于点B(2,0),D(10,0),顶点坐标为F(m2,k).
(1)连接EF,求线段EF的长;
(2)点M(﹣7,d1)在抛物线L1上,点N(16,d2)在抛物线L2上.比较大小:d1 d2;
(3)若点P(n+3,f1),Q(2n﹣1,f2)在抛物线L1上,f1<f2,求n的取值范围.
19.如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(1,0)两点.交y轴于点C.
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,使得S△PBC=S△ABC,若存在,请直接写出点P的坐标;若不存在,请说明理由.
20.数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性,形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
21.综合与探究:如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为,连接.
(1)求A,B,C三点的坐标;
(2)当的面积等于的面积的时,求m的值;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试探究是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案
一、单选题
1.
【分析】由题干条件可以得出二次函数解析式y=﹣(x+1)2+4,再分别判断四个选项,也可以通过二次函数对称性去判断.
【解答】解:选项A:∵顶点坐标为(﹣1,4),∴对称轴为直线x=﹣1,故选项A错误;
选项B:由对称性可知,(﹣3,0)关于x=﹣1对称的点为(1,0),故选项B错误;
选项C:开口向下,当x<﹣1时,y随x的增大而增大,故选项C错误;
选项D:设二次函数解析式为y=a(x+1)2+4,将(﹣3,0)代入得a=﹣1,
∴y=﹣(x+1)2+4,令x=0得y=3,
∴二次函数图象与y轴的交点的纵坐标是3,故选项D正确.
故选:D.
2.
【分析】由抛物线开口方向,对称轴位置,抛物线与y轴交点位置可判断①,由抛物线与x轴交点个数可判断②,由b=﹣2a,x=﹣1时y<0可判断③,由x=1时函数取最大值可判断④,由函数y=ax2+bx+c与直线y=1及直线y=﹣1的交点横坐标为方程|ax2+bx+c|=1的解及抛物线的对称轴为直线x=1可判断⑤.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①错误.
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,
∴b2>4ac,②错误.
∵x=﹣1时,y<0,
∴a﹣b+c<0,
∵b=﹣2a,
∴a,
∴b+c<0,
∴2c<3b,③正确.
∵x=1时,y=a+b+c为函数最大值,
∴a+b+c>m(am+b)+c(m≠1),
∴a+b>m(am+b)(m≠1),
∵b>0,
∴a+2b>a+b>m(am+b)(m≠1),④正确.
方程|ax2+bx+c|=1的四个根分别为ax2+bx+c=1和ax2+bx+c=﹣1的根,
∵抛物线y=ax2+bx+c关于直线x=1对称,
∴抛物线与直线y=1的交点的横坐标为之和为2,
抛物线与直线y=﹣1的交点横坐标为之和为2,
∴方程|ax2+bx+c|=1的四个根的和为4,⑤错误.
故选:A.
3.
【分析】根据抛物线经过点(0,﹣4),(3,﹣4)可得抛物线对称轴为直线x,由抛物线经过点(﹣2,6)可得抛物线开口向上,进而求解.
【解答】解:∵抛物线经过点(0,﹣4),(3,﹣4),
∴抛物线对称轴为直线x,
∵抛物线经过点(﹣2,6),
∴当x时,y随x增大而减小,
∴抛物线开口向上,
∴x时,y随x增大而增大,
∴当x>2时,y随x增大而增大,
故选:D.
4.
【分析】根据抛物线与方程、不等式的关系及抛物线的性质求解.
【解答】解:由图象得:a>0,与x轴相交于点(﹣1,0)和(3,0),
∴抛物线的对称轴为直线x1,即1,
∴b+2a=0,
故①是正确的;
由图象得:当x=1,y<0,即a+b+c<0,
故②是错误的;
∵a>0,
∴y=a在x轴的上方,∴y=ax2+bx+c的图象与y=a有两个交点,
故③是正确的;
根据平移得:y=ax2+bx+c的图象向左平移1个单位得y=a(x+1)2+b(x+1)+c的图象,
∴y=a(x+1)2+b(x+1)+c的图象与x轴的交点为(﹣2,0)(2,0),
∴不等式a(x+1)2+b(x+1)+c<0的解集是﹣2<x<2.
故④是正确的;
故选:C.
5.
【分析】求解函数与x轴的交点坐标,如图,当顶点在E(3,1)处时,A点的横坐标最大,求解解析式,再求解当顶点在C(﹣1,4)处时,B点的横坐标最小时的抛物线,再求解函数与x轴的交点坐标即可得到答案.
【解答】解:如图,当顶点在E(3,1)处时,A点的横坐标最大,
设抛物线的表达式为y=a(x﹣3)2+1,代入A(2,0),解得a=﹣1,
则抛物线的表达式为y=﹣(x﹣3)2+1;
如图,当顶点在C(﹣1,4)处时,B点的横坐标最小,
这时抛物线的表达式为y=﹣(x+1)2+4,
当y=0时,y=﹣(x+1)2+4=0,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
∴点B的横坐标的最小值为1.
.
故选:A.
二、填空题
6.
【分析】根据二次函数y=﹣x2+2x+m的图象可以得到其对称轴和与x轴一个交点,由此可以得到抛物线与x轴的另一个交点坐标,然后就可得m的值,那么解方程就能求得一元二次方程的解,可得到函数与x轴的交点,那么x轴上方的函数图象所对应的x的取值即为不等式﹣x2+2x+m>0的解集,对称轴的右侧,y随x的增大而减小.
【解答】解:∵对称轴为x=1,一个根为3,
∴1,
∴x=﹣1,
∴﹣x2+2x+m=0的根为x1=﹣1,x2=3,
∴不等式﹣x2+2x+m>0的解集是﹣1<x<3,
当x>1时,y随x的而减小.
7.
【分析】根据抛物线与x轴的交点问题,可判断x1、x2为方程x2+3x﹣5=0的两根,利用一元二次方程解的定义得到3x1+5,则3x2+15=﹣3(x1+x2)+20,再根据根与系数的关系得到x1+x2=﹣3,然后利用整体代入的方法计算.
【解答】解:∵抛物线y=x2+3x﹣5与x轴的两个交点为(x1,0)、(x2,0),
∴x1、x2为方程x2+3x﹣5=0的两根,
∴3x1﹣5=0,
∴3x1+5,
∴3x2+15=﹣3x1+5﹣3x2+15=﹣3(x1+x2)+20,
∵x1+x2=﹣3,
∴3x2+15=﹣3×(﹣3)+20=29.
故答案为:29.
8.
【分析】先用m的代数式表示出A,B,C的坐标,再作∠OCB的平分线交OB于点G,过点G作GH⊥BC于点H,根据全等和角平分线性质得到用m的代数式表示的GH和GB的长,根据GH和GB的关系即可求出m的值.
【解答】解:在y=﹣x2+2mx+2m+1中,当y=0时,﹣x2+2mx+2m+1=0,
解方程,得x1=﹣1,x2=2m+1,
∵点A在点B的左侧,且m>0,
∴A(﹣1,0),B(2m+1,0),
在y=﹣x2+2mx+2m+1中,当x=0时,y=2m+1,
∴C(0,2m+1),
∴OB=OC=2m+1,
∵∠BOC=90°,
∴∠OBC=45°,
∵EF∥y轴,
∴∠BEF=∠BCO,
∵∠BEF=2∠ACO,
∴∠BCO=2∠ACO,
作∠OCB的平分线交OB于点G,过点G作GH⊥BC于点H,则OG=GH,如图,
∴∠BCO=2∠OCG,GH=GO,
∴∠ACO=∠GCO,
∴△ACO≌△GCO(ASA),
∴OA=OG=GH=1,
∴GB=OB﹣OG=2m+1﹣1=2m,
∵GH⊥BC,∠GBH=45°,
∴△BGH是等腰直角三角形,
∴,
即,
∴.
故答案为:.
9.
【分析】由抛物线的对称性及点D,B的坐标可得点A,C的坐标,进而求解.
【解答】解:∵CD∥x轴,点A,B为抛物线与x轴交点,
∴A,B关于抛物线对称轴对称,C,D关于抛物线对称轴对称,
∵D(6,4),
∴点C坐标为(0,4),
∴抛物线对称轴为直线x=3,
由B(8,0)可得点A坐标为(﹣2,0),
∴S△ABCAB OC20,
故答案为:20.
10.
【分析】利用排除法,先求得直线y=x+m与该图象有两个或三个交点时m的取值,则可求得结论.
【解答】解:由题意,直线y=x+m与函数y的图象恒相交,
①当m>0时,直线y=x+m与直线y=﹣x(x<0)恒相交,
与抛物线y=﹣x2+2x(x>0)至少有一个交点时,
即方程x+m=﹣x2+2x有两个实数根,
∴x2﹣x+m=0.
∴Δ=(﹣1)2﹣4×1×m≥0,
解得:m.
∴当0<m时,直线y=x+m与函数y的图象有两个或三个交点,
∴当m时,直线y=x+m与函数y的图象只有一个交点;
②当m<0时,由图象可知,直线y=x+m与函数y的图象只有一个交点,
综上,若直线y=x+m与该图象只有一个交点,则m的取值范围为m或m<0.
故答案为:m或m<0.
三、解答题
11.解:(1)列表
x ... ﹣1 0 1 2 3 ...
y ... 0 ﹣3 ﹣4 ﹣3 0 ...
描点、连线,
(2)由函数图象知,当抛物线在x轴上方时,x<﹣1或x>3,
∴当﹣1<x<3时,函数值大于0.
12.解:(1)∵抛物线y=ax2+bx+4交x轴于A(﹣4,0)、B(2,0)两点,
∴,
解得:,
∴该抛物线的解析式为yx2﹣x+4;
(2)过点P作PE∥y轴,交AC于点E,如图,
∵抛物线yx2﹣x+4交y轴于点C,
∴C(0,4),
设直线AC的解析式为y=kx+n,则,
解得:,
∴直线AC的解析式为y=x+4,
设P(m,m2﹣m+4),则E(m,m+4),
∴PEm2﹣m+4﹣(m+4)m2﹣2m,
∵OA=OC=4,
∴△ACO是等腰直角三角形,
∴∠ACO=45°,
∵PE∥y轴,
∴∠PEF=∠ACO=45°,
∵PF⊥AC,
∴△PEF是等腰直角三角形,
∴PFPE(m2﹣2m)(m+2)2,
∵0,
∴当m=﹣2时,PF取得最大值,最大值为,此时点P的坐标为(﹣2,4).
13.解:(1)∵对于,
令x=0,可得y=2,
∴B(0,2),
令y=0,可得x2x+2=0,
解得x=﹣1或4,
∴A(﹣1,0),C(4,0),
设直线BC的解析式为y=kx+2,
∴4k+2=0,
解得k
∴直线BC的解析式为yx+2;
(2)过P点作PQ∥y轴交BC于点Q,
设P(t,t2t+2),则Q(t,t+2),
∴PQt2t+2t﹣2t2+2t,
∴S4×(﹣t2+2t)=﹣2t2+4t=﹣2(t﹣1)2+2,
当t=1时,△BCP的面积最大,面积的最大值为2,此时P(1,3).
14.解:(1)当y1=0时,
x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴抛物线与x轴交于A(﹣1,0),B(3,0).
∵直线y2=﹣x+b经过A点,
∴0=﹣(﹣1)+b,
∴b=﹣1;
(2)由(1)知y2=﹣x﹣1,
联立得:x2﹣2x﹣3=﹣x﹣1,
整理得x2﹣x﹣2=0
解得:x=﹣1(舍),x=2,
把x=2代入y=﹣x﹣1,得y=﹣3,
∴C(2,﹣3),
∴S△ABC[3﹣(﹣1)]×|﹣3|=6;
(3)A(﹣1,0),C(2,﹣3),
当x<﹣1或x>2时,抛物线在直线的上方,
∴当y1>y2时,x<﹣1或x>2.
15.解:(1)二次函数y=x2+bx+c的图象经过点A(1,0),B(0,3),将点A,点B代入得:
,
解得:,
∴二次函数解析式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴二次函数图象对称轴为直线x=2,
∵点C与点B关于该二次函数图象的对称轴对称,已知一次函数y=mx+n的图象经过A,C两点,B(0,3),
∴点C的坐标为(4,3),
∵点A的坐标为(1,0),
∴由图可知,当1<x<4时,x2+bx+c<mx+n;
故答案为:1<x<4;
(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴当x=2时,y有最小值﹣1,
当x=1时,y=1﹣4+3=0,
当x=3时,y=9﹣4×3+3=0,
∴当1≤x≤3时,﹣1≤y≤0,
故答案为:﹣1≤y≤0.
16.解:(1)∵二次函数的对称轴为直线x=﹣1,与x轴一个交点坐标为(1,0),
∴二次函数图象与x轴的另一交点为(﹣3,0),
故答案为:(﹣3,0);
(2)设二次函数的表达式为y=a(x+1)2﹣4,
把(1,0)代入解析式得:4a﹣4=0,
解得a=1,
∴二次函数的表达式表达式为y=(x+1)2﹣4;
(3)∵抛物线开口向上,顶点坐标为(﹣1,﹣4),
∴抛物线的最小值为﹣4,
∵﹣1﹣(﹣4)=3>0﹣(﹣1)=1,
∴当x=﹣4时,y=5,
∴当﹣4<x<0时,y的取值范围为﹣4≤y<5,
故答案为:﹣4≤y<5.
17.解:(1)∵抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(4,0),
∴,
解得,
∴抛物线的解析式为y=x2﹣3x﹣4,
∴P(,﹣);
(2)连接OP,
∵A(﹣1,0),B(4,0),C(0,﹣4),P(,﹣);
∴S△OPC==3,
S△BOP==,
S△BOC==8,
∴S△BPC=S△OPC+S△BOP﹣S△BOC=3+﹣8=.
18.解:(1)由题意可得:m1=,m2==6,
∴EF=6﹣3=3;
(2)由题意得:设抛物线L1:y1=a1(x﹣1)(x﹣5),抛物线L2:y2=a2(x﹣2)(x﹣10),
由(1)得:E(3,k),F(6,k),
∴a1(3﹣1)(3﹣5)=a2(6﹣2)(6﹣10),
∴a1=4a2,
∴y1=4a2(x﹣1)(x﹣5),
把x=﹣7代入抛物线L1得:d1=4a2(x﹣1)(x﹣5)=384a2,
把x=16代入物线L2得:d2=a2(x﹣2)(x﹣10)=84a2,
∵a2>0,
∴d1>d2;
故答案为:>;
(3)∵f1<f2,
∴点P离对称轴更近,
∴|n+3﹣3|<|2n﹣1﹣3|,
∴(n+3﹣3)2﹣(2n﹣1﹣3)2<0,
∴(n+2n﹣4)(n﹣2n+4)<0;
∴或,
∴n<或n>4.
19.解:(1)由抛物线与x轴交于A(﹣3,0),B(1,0)两点,代入抛物线y=ax2+bx+3得:
,
解得:;
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)存在,理由如下:
∵A(﹣3,0),B(1,0),
∴AB=4,
抛物线y=ax2+bx+3与y轴交于点C,
令x=0,则y=3,
∴C点坐标为(0,3),OC=3,
∴S△ABC=AB OC=×4×3=6,
∴S△PBC=S△ABC=3;
作PE∥x轴交BC于E,如图:
设BC的解析式为:y=kx+b,将B、C代入得:
,
解得:,
∴BC的解析式为:y=﹣3x+3;
设点P的横坐标为t,则P(t,﹣t2﹣2t+3),
则E的纵坐标为:﹣3x+3=﹣t2﹣2t+3,解得:x=,
∴E(,﹣t2﹣2t+3);
∴PE=﹣t=,
∴S△PBC=××3=3,
解得:t=﹣2或3;
∴P点纵坐标为:﹣(﹣2)2﹣2×(﹣2)+3=3;或﹣(3)2﹣2×(3)+3=﹣12,
∴点P的坐标为(﹣2,3)或(3,﹣12).
20.(1)证明:当a=﹣时,函数表达式为y=12x+6,
令y=0得x=﹣,
∴此时函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象与x轴有交点;
当a≠时,y=(4a+2)x2+(9﹣6a)x﹣4a+4为二次函数,
∵Δ=(9﹣6a)2﹣4(4a+2)(﹣4a+4)=100a2﹣140a+49=(10a﹣7)2≥0,
∴函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象与x轴有交点;
综上所述,无论a取什么实数,图象T与x轴总有公共点;
(2)解:存在整数a,使图象T与x轴的公共点中有整点,理由如下:
当a=﹣时,不符合题意;
当a≠时,
在y=(4a+2)x2+(9﹣6a)x﹣4a+4中,令y=0得:0=(4a+2)x2+(9﹣6a)x﹣4a+4,
解得x=﹣或x=,
∵x==2﹣,a是整数,
∴当2a+1是6的因数时,是整数,
∴2a+1=﹣6或2a+1=﹣3或2a+1=﹣2或2a+1=﹣1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,
解得a=﹣或a=﹣2或a=﹣或a=﹣1或a=0或a=或a=1或a=,
∵a是整数,
∴a=﹣2或a=﹣1或a=0或a=1.
21.(1)由,得.
解,得,.
∴点A,B的坐标分别为,,
由,得.
∴点C的坐标为.
(2)如图,过点D作轴于E,交BC于G,
过点C作交的延长线于F.
∵点A的坐标为,点C的坐标为.
∴,.
∴.
∴.
∵点B的坐标为,点C的坐标为,
设直线BC的函数表达式为.则.解得
∴直线BC的函数表达式为:.
∵点D的横坐标为,
∴点D的坐标为,点G的坐标为:.
∴,,.
∴
∴.
解得:(不合题意舍去),,
∴m的值为3.
(3)将代入
∴,
设,,
∵,
∴如图所示,当是平行四边形的边时,
∴由平行四边形的性质可得,
,解得或
∴点M的坐标为或;
当是平行四边形的边时,
∴由平行四边形的性质可得,
,解得或(不合题意,应舍去)
∴点M的坐标为;
如图所示,当是平行四边形的对角线时,
∴由平行四边形的性质可得,
,解得或(不合题意,应舍去)
∴点M的坐标为;
综上所述,点M的坐标为或或或.
一、单选题
1.如图,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是﹣3,顶点坐标为(﹣1,4),则下列说法正确的是( )
A.二次函数图象的对称轴是直线x=1
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当x<﹣1时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0; ②b2<4ac; ③2c<3b; ④a+2b>m(am+b)(m≠1);
⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为2,
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
3.表中列出的是一个二次函数的自变量x与函数y的几组对应值:
x … ﹣2 0 1 3 …
y … 6 ﹣4 ﹣6 ﹣4 …
下列各选项中,正确的是( )
A.这个函数的最小值为﹣6
B.这个函数的图象开口向下
C.这个函数的图象与x轴无交点
D.当x>2时,y的值随x值的增大而增大
4.二次函数y=ax2+bx+c的图象如图所示.下列结论:
①2a+b=0;
②a+b+c>0;
③方程ax2+bx+c=a有两个不相等的实数根;
④不等式a(x+1)2+b(x+1)+c<0的解集是﹣2<x<2.
其中所有正确结论的序号是( )
A.①③ B.②④ C.①③④ D.①②③④
5.如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点A的横坐标的最大值为2,则点B的横坐标的最小值为( )
A.1 B.2 C.3 D.4
二、填空题
6.已知二次函数y=﹣x2+2x+m的图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的根为 ;不等式﹣x2+2x+m>0的解集是 ;当x 时,y随x的增大而减小.
7.已知抛物线y=x2+3x﹣5与x轴的两个交点为(x1,0)、(x2,0),则3x2+15= .
8.如图,二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC.若∠BEF=2∠ACO,则m的值为 .
9.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C.过点C作CD⊥y轴,交该图象于点D.若B(8,0)、D(6,4),则△ABC的面积为 .
10.已知函数y的图象如图所示,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .
三、解答题
11.已知抛物线y=x2﹣2x﹣3.
(1)在所给的坐标系中画出这条抛物线;
(2)利用图象回答:x取什么值时,函数值小于0?
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于A(﹣4,0)、B(2,0)两点,交y轴于点C,连接AC.
(1)求抛物线的解析式;
(2)点P为线段AC上方的抛物线上一动点,过P作PF⊥AC,当PF最大时,求出此时P点的坐标以及PF的最大值.
13.如图已知二次函数图象与x轴交于A,C两点,与y轴交于点B.
(1)连结BC,求直线BC的解析式;
(2)点P为该二次函数图象在第一象限上一点,当△BCP的面积最大时,求P点的坐标及△BCP面积的最大值.
14.如图,二次函数的图象与x轴交于点A,B(A在B的左侧),与一次函数y2=﹣x+b的图象交于A,C两点.
(1)求b的值;
(2)求△ABC的面积;
(3)根据图象,直接写出当y1>y2时x的取值范围.
15.二次函数y=x2+bx+c的图象经过点A(1,0),B(0,3),点C与点B关于该二次函数图象的对称轴对称,已知一次函数y=mx+n的图象经过A,C两点.
(1)求二次函数解析式;
(2)根据图象,写出满足不等式x2+bx+c<mx+n的解集 ;
(3)二次函数y=x2+bx+c,当1≤x≤3时,对应的函数值y的取值范围为 .
16.如图,二次函数图象顶点坐标为(﹣1,﹣4),与x轴一个交点坐标为(1,0).
(1)该函数图象与x轴的另一个交点坐标为 ;
(2)求这个二次函数的表达式;
(3)当﹣4<x<0时,y的取值范围为 .
17.如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C.
(1)求抛物线对应的函数解析式,并直接写出顶点P的坐标;
(2)求△BCP的面积.
注:注抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣,顶点坐标是(,).
18.如图,在平面直角坐标系中,抛物线L1交x轴于点A(1,0),C(5,0),顶点坐标为E(m1,k).抛物线L2交x轴于点B(2,0),D(10,0),顶点坐标为F(m2,k).
(1)连接EF,求线段EF的长;
(2)点M(﹣7,d1)在抛物线L1上,点N(16,d2)在抛物线L2上.比较大小:d1 d2;
(3)若点P(n+3,f1),Q(2n﹣1,f2)在抛物线L1上,f1<f2,求n的取值范围.
19.如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(1,0)两点.交y轴于点C.
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,使得S△PBC=S△ABC,若存在,请直接写出点P的坐标;若不存在,请说明理由.
20.数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性,形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
21.综合与探究:如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为,连接.
(1)求A,B,C三点的坐标;
(2)当的面积等于的面积的时,求m的值;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试探究是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案
一、单选题
1.
【分析】由题干条件可以得出二次函数解析式y=﹣(x+1)2+4,再分别判断四个选项,也可以通过二次函数对称性去判断.
【解答】解:选项A:∵顶点坐标为(﹣1,4),∴对称轴为直线x=﹣1,故选项A错误;
选项B:由对称性可知,(﹣3,0)关于x=﹣1对称的点为(1,0),故选项B错误;
选项C:开口向下,当x<﹣1时,y随x的增大而增大,故选项C错误;
选项D:设二次函数解析式为y=a(x+1)2+4,将(﹣3,0)代入得a=﹣1,
∴y=﹣(x+1)2+4,令x=0得y=3,
∴二次函数图象与y轴的交点的纵坐标是3,故选项D正确.
故选:D.
2.
【分析】由抛物线开口方向,对称轴位置,抛物线与y轴交点位置可判断①,由抛物线与x轴交点个数可判断②,由b=﹣2a,x=﹣1时y<0可判断③,由x=1时函数取最大值可判断④,由函数y=ax2+bx+c与直线y=1及直线y=﹣1的交点横坐标为方程|ax2+bx+c|=1的解及抛物线的对称轴为直线x=1可判断⑤.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①错误.
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,
∴b2>4ac,②错误.
∵x=﹣1时,y<0,
∴a﹣b+c<0,
∵b=﹣2a,
∴a,
∴b+c<0,
∴2c<3b,③正确.
∵x=1时,y=a+b+c为函数最大值,
∴a+b+c>m(am+b)+c(m≠1),
∴a+b>m(am+b)(m≠1),
∵b>0,
∴a+2b>a+b>m(am+b)(m≠1),④正确.
方程|ax2+bx+c|=1的四个根分别为ax2+bx+c=1和ax2+bx+c=﹣1的根,
∵抛物线y=ax2+bx+c关于直线x=1对称,
∴抛物线与直线y=1的交点的横坐标为之和为2,
抛物线与直线y=﹣1的交点横坐标为之和为2,
∴方程|ax2+bx+c|=1的四个根的和为4,⑤错误.
故选:A.
3.
【分析】根据抛物线经过点(0,﹣4),(3,﹣4)可得抛物线对称轴为直线x,由抛物线经过点(﹣2,6)可得抛物线开口向上,进而求解.
【解答】解:∵抛物线经过点(0,﹣4),(3,﹣4),
∴抛物线对称轴为直线x,
∵抛物线经过点(﹣2,6),
∴当x时,y随x增大而减小,
∴抛物线开口向上,
∴x时,y随x增大而增大,
∴当x>2时,y随x增大而增大,
故选:D.
4.
【分析】根据抛物线与方程、不等式的关系及抛物线的性质求解.
【解答】解:由图象得:a>0,与x轴相交于点(﹣1,0)和(3,0),
∴抛物线的对称轴为直线x1,即1,
∴b+2a=0,
故①是正确的;
由图象得:当x=1,y<0,即a+b+c<0,
故②是错误的;
∵a>0,
∴y=a在x轴的上方,∴y=ax2+bx+c的图象与y=a有两个交点,
故③是正确的;
根据平移得:y=ax2+bx+c的图象向左平移1个单位得y=a(x+1)2+b(x+1)+c的图象,
∴y=a(x+1)2+b(x+1)+c的图象与x轴的交点为(﹣2,0)(2,0),
∴不等式a(x+1)2+b(x+1)+c<0的解集是﹣2<x<2.
故④是正确的;
故选:C.
5.
【分析】求解函数与x轴的交点坐标,如图,当顶点在E(3,1)处时,A点的横坐标最大,求解解析式,再求解当顶点在C(﹣1,4)处时,B点的横坐标最小时的抛物线,再求解函数与x轴的交点坐标即可得到答案.
【解答】解:如图,当顶点在E(3,1)处时,A点的横坐标最大,
设抛物线的表达式为y=a(x﹣3)2+1,代入A(2,0),解得a=﹣1,
则抛物线的表达式为y=﹣(x﹣3)2+1;
如图,当顶点在C(﹣1,4)处时,B点的横坐标最小,
这时抛物线的表达式为y=﹣(x+1)2+4,
当y=0时,y=﹣(x+1)2+4=0,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
∴点B的横坐标的最小值为1.
.
故选:A.
二、填空题
6.
【分析】根据二次函数y=﹣x2+2x+m的图象可以得到其对称轴和与x轴一个交点,由此可以得到抛物线与x轴的另一个交点坐标,然后就可得m的值,那么解方程就能求得一元二次方程的解,可得到函数与x轴的交点,那么x轴上方的函数图象所对应的x的取值即为不等式﹣x2+2x+m>0的解集,对称轴的右侧,y随x的增大而减小.
【解答】解:∵对称轴为x=1,一个根为3,
∴1,
∴x=﹣1,
∴﹣x2+2x+m=0的根为x1=﹣1,x2=3,
∴不等式﹣x2+2x+m>0的解集是﹣1<x<3,
当x>1时,y随x的而减小.
7.
【分析】根据抛物线与x轴的交点问题,可判断x1、x2为方程x2+3x﹣5=0的两根,利用一元二次方程解的定义得到3x1+5,则3x2+15=﹣3(x1+x2)+20,再根据根与系数的关系得到x1+x2=﹣3,然后利用整体代入的方法计算.
【解答】解:∵抛物线y=x2+3x﹣5与x轴的两个交点为(x1,0)、(x2,0),
∴x1、x2为方程x2+3x﹣5=0的两根,
∴3x1﹣5=0,
∴3x1+5,
∴3x2+15=﹣3x1+5﹣3x2+15=﹣3(x1+x2)+20,
∵x1+x2=﹣3,
∴3x2+15=﹣3×(﹣3)+20=29.
故答案为:29.
8.
【分析】先用m的代数式表示出A,B,C的坐标,再作∠OCB的平分线交OB于点G,过点G作GH⊥BC于点H,根据全等和角平分线性质得到用m的代数式表示的GH和GB的长,根据GH和GB的关系即可求出m的值.
【解答】解:在y=﹣x2+2mx+2m+1中,当y=0时,﹣x2+2mx+2m+1=0,
解方程,得x1=﹣1,x2=2m+1,
∵点A在点B的左侧,且m>0,
∴A(﹣1,0),B(2m+1,0),
在y=﹣x2+2mx+2m+1中,当x=0时,y=2m+1,
∴C(0,2m+1),
∴OB=OC=2m+1,
∵∠BOC=90°,
∴∠OBC=45°,
∵EF∥y轴,
∴∠BEF=∠BCO,
∵∠BEF=2∠ACO,
∴∠BCO=2∠ACO,
作∠OCB的平分线交OB于点G,过点G作GH⊥BC于点H,则OG=GH,如图,
∴∠BCO=2∠OCG,GH=GO,
∴∠ACO=∠GCO,
∴△ACO≌△GCO(ASA),
∴OA=OG=GH=1,
∴GB=OB﹣OG=2m+1﹣1=2m,
∵GH⊥BC,∠GBH=45°,
∴△BGH是等腰直角三角形,
∴,
即,
∴.
故答案为:.
9.
【分析】由抛物线的对称性及点D,B的坐标可得点A,C的坐标,进而求解.
【解答】解:∵CD∥x轴,点A,B为抛物线与x轴交点,
∴A,B关于抛物线对称轴对称,C,D关于抛物线对称轴对称,
∵D(6,4),
∴点C坐标为(0,4),
∴抛物线对称轴为直线x=3,
由B(8,0)可得点A坐标为(﹣2,0),
∴S△ABCAB OC20,
故答案为:20.
10.
【分析】利用排除法,先求得直线y=x+m与该图象有两个或三个交点时m的取值,则可求得结论.
【解答】解:由题意,直线y=x+m与函数y的图象恒相交,
①当m>0时,直线y=x+m与直线y=﹣x(x<0)恒相交,
与抛物线y=﹣x2+2x(x>0)至少有一个交点时,
即方程x+m=﹣x2+2x有两个实数根,
∴x2﹣x+m=0.
∴Δ=(﹣1)2﹣4×1×m≥0,
解得:m.
∴当0<m时,直线y=x+m与函数y的图象有两个或三个交点,
∴当m时,直线y=x+m与函数y的图象只有一个交点;
②当m<0时,由图象可知,直线y=x+m与函数y的图象只有一个交点,
综上,若直线y=x+m与该图象只有一个交点,则m的取值范围为m或m<0.
故答案为:m或m<0.
三、解答题
11.解:(1)列表
x ... ﹣1 0 1 2 3 ...
y ... 0 ﹣3 ﹣4 ﹣3 0 ...
描点、连线,
(2)由函数图象知,当抛物线在x轴上方时,x<﹣1或x>3,
∴当﹣1<x<3时,函数值大于0.
12.解:(1)∵抛物线y=ax2+bx+4交x轴于A(﹣4,0)、B(2,0)两点,
∴,
解得:,
∴该抛物线的解析式为yx2﹣x+4;
(2)过点P作PE∥y轴,交AC于点E,如图,
∵抛物线yx2﹣x+4交y轴于点C,
∴C(0,4),
设直线AC的解析式为y=kx+n,则,
解得:,
∴直线AC的解析式为y=x+4,
设P(m,m2﹣m+4),则E(m,m+4),
∴PEm2﹣m+4﹣(m+4)m2﹣2m,
∵OA=OC=4,
∴△ACO是等腰直角三角形,
∴∠ACO=45°,
∵PE∥y轴,
∴∠PEF=∠ACO=45°,
∵PF⊥AC,
∴△PEF是等腰直角三角形,
∴PFPE(m2﹣2m)(m+2)2,
∵0,
∴当m=﹣2时,PF取得最大值,最大值为,此时点P的坐标为(﹣2,4).
13.解:(1)∵对于,
令x=0,可得y=2,
∴B(0,2),
令y=0,可得x2x+2=0,
解得x=﹣1或4,
∴A(﹣1,0),C(4,0),
设直线BC的解析式为y=kx+2,
∴4k+2=0,
解得k
∴直线BC的解析式为yx+2;
(2)过P点作PQ∥y轴交BC于点Q,
设P(t,t2t+2),则Q(t,t+2),
∴PQt2t+2t﹣2t2+2t,
∴S4×(﹣t2+2t)=﹣2t2+4t=﹣2(t﹣1)2+2,
当t=1时,△BCP的面积最大,面积的最大值为2,此时P(1,3).
14.解:(1)当y1=0时,
x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴抛物线与x轴交于A(﹣1,0),B(3,0).
∵直线y2=﹣x+b经过A点,
∴0=﹣(﹣1)+b,
∴b=﹣1;
(2)由(1)知y2=﹣x﹣1,
联立得:x2﹣2x﹣3=﹣x﹣1,
整理得x2﹣x﹣2=0
解得:x=﹣1(舍),x=2,
把x=2代入y=﹣x﹣1,得y=﹣3,
∴C(2,﹣3),
∴S△ABC[3﹣(﹣1)]×|﹣3|=6;
(3)A(﹣1,0),C(2,﹣3),
当x<﹣1或x>2时,抛物线在直线的上方,
∴当y1>y2时,x<﹣1或x>2.
15.解:(1)二次函数y=x2+bx+c的图象经过点A(1,0),B(0,3),将点A,点B代入得:
,
解得:,
∴二次函数解析式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴二次函数图象对称轴为直线x=2,
∵点C与点B关于该二次函数图象的对称轴对称,已知一次函数y=mx+n的图象经过A,C两点,B(0,3),
∴点C的坐标为(4,3),
∵点A的坐标为(1,0),
∴由图可知,当1<x<4时,x2+bx+c<mx+n;
故答案为:1<x<4;
(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴当x=2时,y有最小值﹣1,
当x=1时,y=1﹣4+3=0,
当x=3时,y=9﹣4×3+3=0,
∴当1≤x≤3时,﹣1≤y≤0,
故答案为:﹣1≤y≤0.
16.解:(1)∵二次函数的对称轴为直线x=﹣1,与x轴一个交点坐标为(1,0),
∴二次函数图象与x轴的另一交点为(﹣3,0),
故答案为:(﹣3,0);
(2)设二次函数的表达式为y=a(x+1)2﹣4,
把(1,0)代入解析式得:4a﹣4=0,
解得a=1,
∴二次函数的表达式表达式为y=(x+1)2﹣4;
(3)∵抛物线开口向上,顶点坐标为(﹣1,﹣4),
∴抛物线的最小值为﹣4,
∵﹣1﹣(﹣4)=3>0﹣(﹣1)=1,
∴当x=﹣4时,y=5,
∴当﹣4<x<0时,y的取值范围为﹣4≤y<5,
故答案为:﹣4≤y<5.
17.解:(1)∵抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(4,0),
∴,
解得,
∴抛物线的解析式为y=x2﹣3x﹣4,
∴P(,﹣);
(2)连接OP,
∵A(﹣1,0),B(4,0),C(0,﹣4),P(,﹣);
∴S△OPC==3,
S△BOP==,
S△BOC==8,
∴S△BPC=S△OPC+S△BOP﹣S△BOC=3+﹣8=.
18.解:(1)由题意可得:m1=,m2==6,
∴EF=6﹣3=3;
(2)由题意得:设抛物线L1:y1=a1(x﹣1)(x﹣5),抛物线L2:y2=a2(x﹣2)(x﹣10),
由(1)得:E(3,k),F(6,k),
∴a1(3﹣1)(3﹣5)=a2(6﹣2)(6﹣10),
∴a1=4a2,
∴y1=4a2(x﹣1)(x﹣5),
把x=﹣7代入抛物线L1得:d1=4a2(x﹣1)(x﹣5)=384a2,
把x=16代入物线L2得:d2=a2(x﹣2)(x﹣10)=84a2,
∵a2>0,
∴d1>d2;
故答案为:>;
(3)∵f1<f2,
∴点P离对称轴更近,
∴|n+3﹣3|<|2n﹣1﹣3|,
∴(n+3﹣3)2﹣(2n﹣1﹣3)2<0,
∴(n+2n﹣4)(n﹣2n+4)<0;
∴或,
∴n<或n>4.
19.解:(1)由抛物线与x轴交于A(﹣3,0),B(1,0)两点,代入抛物线y=ax2+bx+3得:
,
解得:;
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)存在,理由如下:
∵A(﹣3,0),B(1,0),
∴AB=4,
抛物线y=ax2+bx+3与y轴交于点C,
令x=0,则y=3,
∴C点坐标为(0,3),OC=3,
∴S△ABC=AB OC=×4×3=6,
∴S△PBC=S△ABC=3;
作PE∥x轴交BC于E,如图:
设BC的解析式为:y=kx+b,将B、C代入得:
,
解得:,
∴BC的解析式为:y=﹣3x+3;
设点P的横坐标为t,则P(t,﹣t2﹣2t+3),
则E的纵坐标为:﹣3x+3=﹣t2﹣2t+3,解得:x=,
∴E(,﹣t2﹣2t+3);
∴PE=﹣t=,
∴S△PBC=××3=3,
解得:t=﹣2或3;
∴P点纵坐标为:﹣(﹣2)2﹣2×(﹣2)+3=3;或﹣(3)2﹣2×(3)+3=﹣12,
∴点P的坐标为(﹣2,3)或(3,﹣12).
20.(1)证明:当a=﹣时,函数表达式为y=12x+6,
令y=0得x=﹣,
∴此时函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象与x轴有交点;
当a≠时,y=(4a+2)x2+(9﹣6a)x﹣4a+4为二次函数,
∵Δ=(9﹣6a)2﹣4(4a+2)(﹣4a+4)=100a2﹣140a+49=(10a﹣7)2≥0,
∴函数y=(4a+2)x2+(9﹣6a)x﹣4a+4(实数a为常数)的图象与x轴有交点;
综上所述,无论a取什么实数,图象T与x轴总有公共点;
(2)解:存在整数a,使图象T与x轴的公共点中有整点,理由如下:
当a=﹣时,不符合题意;
当a≠时,
在y=(4a+2)x2+(9﹣6a)x﹣4a+4中,令y=0得:0=(4a+2)x2+(9﹣6a)x﹣4a+4,
解得x=﹣或x=,
∵x==2﹣,a是整数,
∴当2a+1是6的因数时,是整数,
∴2a+1=﹣6或2a+1=﹣3或2a+1=﹣2或2a+1=﹣1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,
解得a=﹣或a=﹣2或a=﹣或a=﹣1或a=0或a=或a=1或a=,
∵a是整数,
∴a=﹣2或a=﹣1或a=0或a=1.
21.(1)由,得.
解,得,.
∴点A,B的坐标分别为,,
由,得.
∴点C的坐标为.
(2)如图,过点D作轴于E,交BC于G,
过点C作交的延长线于F.
∵点A的坐标为,点C的坐标为.
∴,.
∴.
∴.
∵点B的坐标为,点C的坐标为,
设直线BC的函数表达式为.则.解得
∴直线BC的函数表达式为:.
∵点D的横坐标为,
∴点D的坐标为,点G的坐标为:.
∴,,.
∴
∴.
解得:(不合题意舍去),,
∴m的值为3.
(3)将代入
∴,
设,,
∵,
∴如图所示,当是平行四边形的边时,
∴由平行四边形的性质可得,
,解得或
∴点M的坐标为或;
当是平行四边形的边时,
∴由平行四边形的性质可得,
,解得或(不合题意,应舍去)
∴点M的坐标为;
如图所示,当是平行四边形的对角线时,
∴由平行四边形的性质可得,
,解得或(不合题意,应舍去)
∴点M的坐标为;
综上所述,点M的坐标为或或或.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
