6.4 数学思考(教学课件)(共20张PPT)——小学数学人教版六年级下册
文档属性
| 名称 | 6.4 数学思考(教学课件)(共20张PPT)——小学数学人教版六年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1015.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 14:05:31 | ||
图片预览







文档简介
(共20张PPT)
数学思考
巩固旧知
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
巩固旧知
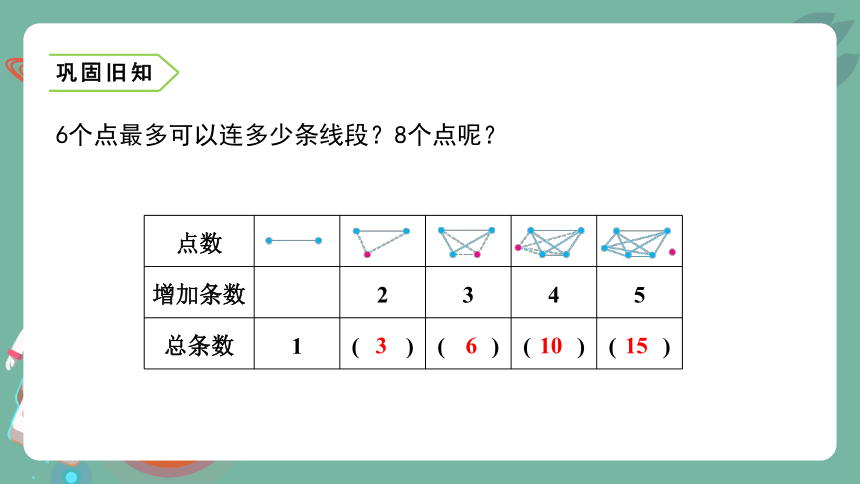
6个点最多可以连多少条线段?8个点呢?
点数
增加条数 2 3 4 5
总条数 1 ( ) ( ) ( ) ( )
3
6
10
15
巩固旧知
观察表格发现:从2个点开始,以后每增加1个点,这个点和原来的每个点连成1条线段,所以原来有几个点,就会相应增加几条线段。即:
1个点连成线段的条数:0条
2个点连成线段的条数:1条
3个点连成线段的条数:1+2=3(条)
巩固旧知
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:
1+2+3+4+5=(1+5)×5÷2=15(条)
8个点连成线段的条数:
1+2+3+4+5+6+7=(1+7)×7÷2=28(条)
巩固旧知
根据规律,你知道12个点、20个点最多能连多少条线段吗?请写出算式。想一想:n点最多能连多少条线段?
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11=(1+11)×11÷2=66(条)
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19=(1+19)×19÷2=190(条)
巩固旧知
n个点连成线段的条数:
1+2+3+4+……+(n-2)+(n-1)
=(1+n-1)×(n-1)÷2
= (条)
做一做
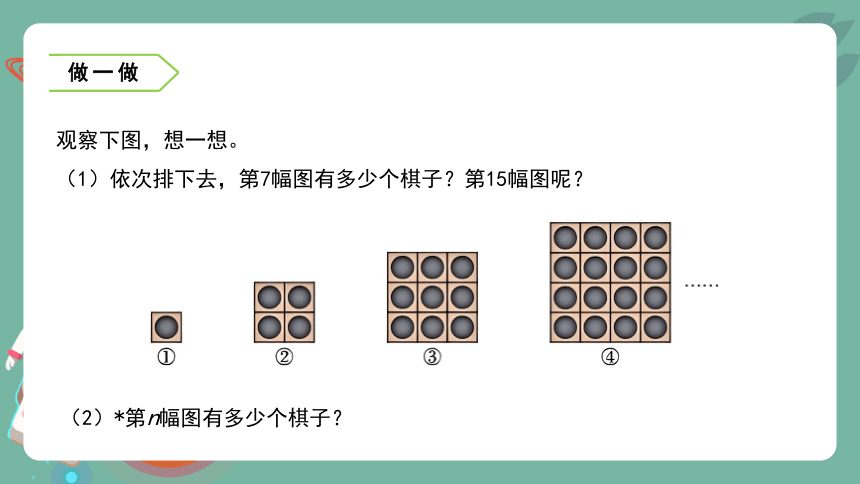
观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
(2)*第n幅图有多少个棋子?
巩固旧知
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、 F。请问:哪两位班长是同班的?
巩固旧知
用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第1次 1 1 1 0 0 0
第2次 0 1 0 1 1 0
第3次 1 0 0 0 1 1
巩固旧知
从第一次到会的情况可以看出,A只可能和D、E、F同班;从第二次到会的情况可以判断,A只可能和D、E同班;从第三次到会的情况可以确定,A只可能和D同班。
从第一次到会情况可看出B可能和E、F同班,从第二次到会的情况可以看出B和F同班,从而可知C和E同班。
王阿姨、刘阿姨、丁叔叔、李叔叔的职业分别是工人、教师、医生中的一种。王阿姨是教师,丁叔叔不是工人,只有刘阿姨和李叔叔的职业相同。请问:他们的职业分别是什么?
做一做
王阿姨:教师;丁叔叔:医生;
刘阿姨:工人;李叔叔:工人。
巩固旧知
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于3个□的和,把△+□=24中的△换成□+□+□,得到□+□+□+□=24,即4×□=24,所以□=6。把□=6代入△=□+□+□中,可算出△=6×3=18。
巩固旧知
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,根据等式的性质1,两个等式的两边都减去☆;得到○=160-☆,◎=160-☆,因为☆代表同一个数,所以○=◎。也可以这样想:由○+☆=160,◎+☆=160,根据等式的性质3,可知:○+☆=◎+☆,根据等式的性质1,等式两边同时减去☆,得到○=◎。
巩固旧知
2. 什么是平角?平角与直线有什么区别?如下图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?
(2)你能推出∠1=∠3吗?
想:平角的两边在一条直线上。
想:∠1和∠2,∠2和∠3都能组成平角。
巩固旧知
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2,∠3=180°-∠2。
因为180°-∠2=180°-∠2,所以∠1=∠3。
巩固练习
1.某大楼共悬挂59盏霓虹灯,这些灯是按照1黄、2绿、3蓝、4红、1黄、2绿、3蓝、4红……的顺序排列的,最后一盏灯的颜色是( )色的。
A.黄 B.绿 C.蓝 D.红
D
巩固练习
2.用火柴棒摆金鱼,根据规律填一填。
8根 ( )根 ( )根 ( )根
14
20
44
巩固练习
3.如图,第5行第1个数是( ),第20行第5个数是( )。
17
366
感谢观看
数学思考
巩固旧知
数学思想和方法可以帮助我们有条理地思考,简便地解决问题。你能举例说一说你知道哪些数学思想和方法吗?
巩固旧知
6个点最多可以连多少条线段?8个点呢?
点数
增加条数 2 3 4 5
总条数 1 ( ) ( ) ( ) ( )
3
6
10
15
巩固旧知
观察表格发现:从2个点开始,以后每增加1个点,这个点和原来的每个点连成1条线段,所以原来有几个点,就会相应增加几条线段。即:
1个点连成线段的条数:0条
2个点连成线段的条数:1条
3个点连成线段的条数:1+2=3(条)
巩固旧知
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:
1+2+3+4+5=(1+5)×5÷2=15(条)
8个点连成线段的条数:
1+2+3+4+5+6+7=(1+7)×7÷2=28(条)
巩固旧知
根据规律,你知道12个点、20个点最多能连多少条线段吗?请写出算式。想一想:n点最多能连多少条线段?
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11=(1+11)×11÷2=66(条)
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19=(1+19)×19÷2=190(条)
巩固旧知
n个点连成线段的条数:
1+2+3+4+……+(n-2)+(n-1)
=(1+n-1)×(n-1)÷2
= (条)
做一做
观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
(2)*第n幅图有多少个棋子?
巩固旧知
六年级有3个班,每班有2个班长。开班长会时,每次只要每班一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、 F。请问:哪两位班长是同班的?
巩固旧知
用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第1次 1 1 1 0 0 0
第2次 0 1 0 1 1 0
第3次 1 0 0 0 1 1
巩固旧知
从第一次到会的情况可以看出,A只可能和D、E、F同班;从第二次到会的情况可以判断,A只可能和D、E同班;从第三次到会的情况可以确定,A只可能和D同班。
从第一次到会情况可看出B可能和E、F同班,从第二次到会的情况可以看出B和F同班,从而可知C和E同班。
王阿姨、刘阿姨、丁叔叔、李叔叔的职业分别是工人、教师、医生中的一种。王阿姨是教师,丁叔叔不是工人,只有刘阿姨和李叔叔的职业相同。请问:他们的职业分别是什么?
做一做
王阿姨:教师;丁叔叔:医生;
刘阿姨:工人;李叔叔:工人。
巩固旧知
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于3个□的和,把△+□=24中的△换成□+□+□,得到□+□+□+□=24,即4×□=24,所以□=6。把□=6代入△=□+□+□中,可算出△=6×3=18。
巩固旧知
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,根据等式的性质1,两个等式的两边都减去☆;得到○=160-☆,◎=160-☆,因为☆代表同一个数,所以○=◎。也可以这样想:由○+☆=160,◎+☆=160,根据等式的性质3,可知:○+☆=◎+☆,根据等式的性质1,等式两边同时减去☆,得到○=◎。
巩固旧知
2. 什么是平角?平角与直线有什么区别?如下图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?
(2)你能推出∠1=∠3吗?
想:平角的两边在一条直线上。
想:∠1和∠2,∠2和∠3都能组成平角。
巩固旧知
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2,∠3=180°-∠2。
因为180°-∠2=180°-∠2,所以∠1=∠3。
巩固练习
1.某大楼共悬挂59盏霓虹灯,这些灯是按照1黄、2绿、3蓝、4红、1黄、2绿、3蓝、4红……的顺序排列的,最后一盏灯的颜色是( )色的。
A.黄 B.绿 C.蓝 D.红
D
巩固练习
2.用火柴棒摆金鱼,根据规律填一填。
8根 ( )根 ( )根 ( )根
14
20
44
巩固练习
3.如图,第5行第1个数是( ),第20行第5个数是( )。
17
366
感谢观看
